

| ホームページ | Pirikaで化学 | ブログ | 業務リスト | お問い合わせ |
| Pirikaで化学トップ | 情報化学+教育 | HSP | 化学全般 |
| 情報化学+教育トップ | 情報化学 | MAGICIAN | MOOC | プログラミング |
| MAGICIANトップ | MAGICIAN-Jr. | MAGICIAN-講義 | 過去の資料 |
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)とネットワーク(Networks)を結びつけて(Associate)いかれる人材です。
2021.8.23
数独(SuDoku)というのはご存知だろうか?
縦、横、3*3の大きなマス目に同じ番号は1度だけ使って空欄を埋めていくゲームだ。
その化学バージョンを作ってみた。
ボタンを押すたびに違うパターンの問題を作成してくれる。
プログラムのほとんどは、前回作成したパーコレーション・ソフトを流用した。
数字のところに何を表示するかは自由なので、音符や果物なんでも良い。
var GenSo=["H","He","Li","Be","B","C","N","O","F"];var GenSo=["𝄞","♩","♪","♫","♬","♮","♭","♯","𝄡"];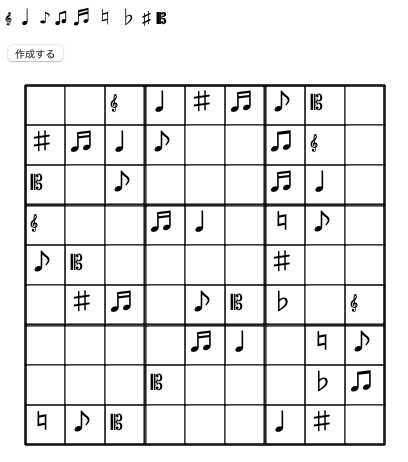
ここで大事なのは、おおもとの答えは先に準備することだ。自分で1問解いてみてその答えを準備するのでも良い。
st=
[[1,4,7,2,5,8,3,6,9],
[2,5,8,3,6,9,4,7,1],
[3,6,9,4,7,1,5,8,2],
[4,7,1,5,8,2,6,9,3],
[5,8,2,6,9,3,7,1,4],
[6,9,3,7,1,4,8,2,5],
[7,1,4,8,2,5,9,3,6],
[8,2,5,9,3,6,1,4,7],
[9,3,6,1,4,7,2,5,8]];僕は、ネットに転がっていたこれをベースにすることにした。
そしていつものように、コインを投げて、表が出たらそのマス目を隠す。
確率は0.5にしておく。(場合によって隠されたものが多くなりすぎて答えが無くなることもある。)
それだけだと、隠される位置はランダムになるが、パターンは同じなので、一度解いたら後は隠されているところに何があるか分かってしまう。
そこでシャッフルすることを考える。
第7回で連立方程式の吐き出し法の説明を行なった。

順番にお掃除、お掃除
|
連立方程式は次のようになる。 X(1) *10 + X(2) *8 + X(3) *0 + X(4) *0=128 X(1) *8 + X(2) *18 + X(3) *0 + X(4) *0=114 X(1) *4 + X(2) *10 + X(3) *1 + X(4) *0=74 X(1) *0 + X(2) *3 + X(3) *0 + X(4) *1=17 |
こうした、連立方程式は、行をいくら入れ替えても答えは変わらない。
またX(1)やX(2)の列を入れ替えても答えは変わらない。
この連立方程式を係数だけを取り出したA行列と、X列と答えのB列とみなすと、
A・X=B
のように書ける。
そしてこの式も行同志、列同志を入れ替えても良い。
この入れ替えを化独に使う。
|
この9*9の小マス目を、3*3の中マス目9個で見る。 それを横のゾーン3つ、縦のゾーン3つと見る。 同じ横ゾーン内部の行、列ゾーン内部の列は入れ替えても良い。 ゾーンブロック同士は入れ替えても良い。(3列とか3行単位で入れ替え) ゾーンをまたいだ入れ替えはできない。 |
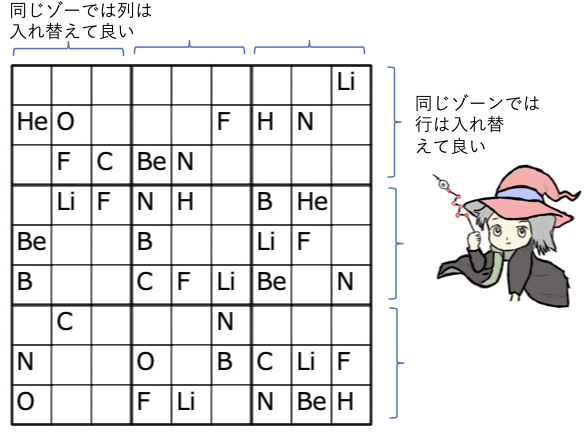
同じ横ゾーン内の行は入れ替えても良い。
|
ライブラリーを使えば簡単にスワップできるが、地道に値を保護しておいて入れ替えるやり方を学ぼう。
同じものが選ばれて変化しないこともある。
for(var i=0;i<3;i++){// 3つのブロック
var gyou1=Math.floor(Math.random()*3) ;//同じゾーンのどれか1行
var gyou2=Math.floor(Math.random()*3) ;//じゾーンのどれか1行
for(var j=0;j<9;j++){
gyouH[j]=st[i*3+gyou2][j];//一旦保護しておく。
}
for(var j=0;j<9;j++){
st[i*3+gyou2][j]=st[i*3+gyou1][j];//gyou2にgyou1をコピー
}
for(var j=0;j<9;j++){
st[i*3+gyou1][j]=gyouH[j];//gyou1に保護したものを戻す。
}
}列についても同じように入れ替える。
隠された場所、隠された量によっては、答えが出せないこともある。
まーそれも愛嬌で、世の中、答えがある問題ばかりでは無い。
プログラムにはしていないが、考え方だけ示しておこう。
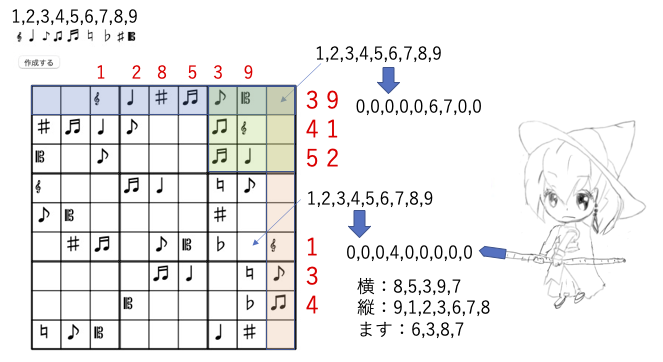
このマス目は4番に決定!
|
最初隠されたますに、1-9の番号を入れる。
縦、横、ますに何が入っているか調べ、使われていない番号を得る。
右上のマスは、6,7ではあるが決定できない。
中段のマス目は、4しか残らないので、決定になる。
決定が出るたびに、未決定のものを調べなおす。
最後まで未決定のものがあれば、その問題は解けないので、捨ててやり直す。
難問を作りたかったら、解けると分かった段階で、
ランダムに隠すものを選んで、解けるかチェック
解けなかったら、他のものを選んで、解けるかチェック
解けたら、さらに隠すものを増やす。
これを繰り返す。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。