pirika logo

ホームページ Pirikaで化学 ブログ 業務リスト お問い合わせ
Pirikaで化学トップ 情報化学+教育 HSP 化学全般
情報化学+教育トップ 情報化学 MAGICIAN MOOC プログラミング
MAGICIANトップ MAGICIAN-Jr. MAGICIAN-講義 過去の資料

MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)とネットワーク(Networks)を結びつけて(Associate)いかれる人材です。

MAGICIANトップ > 高校生にもわかる化学、薬学系 データサイエンス MAGICIAN-Jr. > 第5回

2021.7.22

第5回乱数を使った化学系プログラミング　モンテカルロ法

C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C=C

生体の高分子と、人が作った高分子どこが違うのだろうか？
最近の高分子化学はずいぶん進歩して、分子の大きさやモノマーの並び順を制御できるようになってきた。
しかし、身の回りで見かけるポリマー（プラスティック）の分子量は広い分布を持っている。
それに対して、生体の中で作られるポリマー（タンパク質など）は設計図（DNA→RNA)に従って高度に制御されている。

どういうポリマーができるかは設計図に聞く。
どういうポリマーができるかはサイコロに聞く。

第4回で乱数の使い方を覚えたのだから、実際にサイコロを投げてポリマーを作ってみよう。
その前提として、高分子がどのようにできるかを理解しておこう。
ここでは、開始剤にモノマーがラジカル付加するラジカル重合をイメージしている。
難しいことはともかく、オレンジ色の球に青い球がだんだんくっついて長い鎖ができる。
オレンジ色の球が複数ある時には、どの末端にくっつくかは”乱数”で決まる。

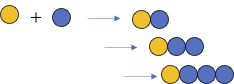
ポリマーはモノマーが開始剤に順番に付いてだんだん大きくなる
開始剤が複数あるので、1本1本の高分子の鎖の長さはまちまちになる。

モンテカルロ　重合反応シミュレーション

モンテカルロというのは、カジノで有名なモナコ公国にある。カジノといえばサイコロ。

まずはサイコロを作ってみよう。
クリックするたびに、違う1-6の間の数が表示される。


サイコロの目： ***

前回作ったプログラムのJavaScriptの部分を次のように書き直せば良い。 

var randnum =Math.floor(Math.random()*6)+1  ;

Math.random()を6倍してfloorを取ると0-5の自然数をランダムに返す。それに1を足すと1-6の値をランダムに返すことになる。

それでは、次に箱に番号を振っておいて、サイコロの目の箱にモノマーを入れていくことを考える。

どの箱が選ばれるかは1/6でどれも同じ！

箱が6個あるので、全部で6*10=60個のモノマーをサイコロによって割り振ってみる。
どの箱が選ばれるかは確率1/6なのでどれも同じだ。
だから、どの箱にも10個モノマーが入っていくように思うかもしれない。

実際にやってみるとどうだろう？


箱1： 0
箱2： 0
箱3： 0
箱4： 0
箱5： 0
箱6： 0

乱数は、やるたびに変わるので、ボタンを押すたびに違う答えになるが、結構値が変わるのでびっくりする。

プログラム作成

それではプログラムをどう変えるのかを見ていこう。

結果を表示するhtmlの部分は箱の数だけ用意する。
そのidはsample1-6の6つにする。そのidのところに箱の中の数が表示される。 

箱1： <span id="sample1">0</span><br>
箱2： <span id="sample2">0</span><br>

箱6： <span id="sample6">0</span><br>

実際の計算はJavaScriptの中で行う。
先に結果を表示させる部分を見てみよう。 sample1-6の位置にHako1-6の変数を表示させている。

   document.getElementById("sample1").innerHTML =Hako1;
   document.getElementById("sample2").innerHTML =Hako2;

   document.getElementById("sample6").innerHTML =Hako6;

関数の中では変数Hako1-6を準備する。
変数の中身は0で初期化しておく。

  var Hako1=0;
  var Hako2=0;

  var Hako6=0;
  
  var randnum;

今回、新しいプログラミングのテクニックで、繰り返し計算の方法を覚えよう。
for(var i=0;i<60;i++){

}
これは、変数iの値を0から60未満の間（全部で0-59の60回）iの数を1つづつ増やしながら
{ }の間を繰り返しなさいという命令になる。

  for(var i=0;i<60;i++){
    randnum=Math.floor(Math.random()*6)+1  ;
    if(randnum==1){Hako1 +=1;}
    if(randnum==2){Hako2 +=1;}

    if(randnum==6){Hako6 +=1;}
   }

randnum=Math.floor(Math.random()*6)+1 ; は1-6の乱数をrandnum変数に代入しなさいという命令だ。

そして、
if(randnum==1){Hako1 +=1;}
は前回やった条件分岐のやり方だ。
もし、randnumが１であったら（＝が2回続くのに注意）Hako1の中身を1つ増やすという命令になる。

Hako1 +=1;という書き方はちょっと難しいかもしれない。
(新しい）Hako1=(古い）Hako1 +1; はプログラムでは
Hako1=Hako1+1; と書くところを
Hako1 += 1; と省略できる。

次のプログラムをMonte.htmlとしてセーブして60を600、6000と変えながら結果を見てみよう。 回数を増やすと平均からの誤差％はどう変わっていくだろうか？　調べてみよう。 

<!DOCTYPE html>
<html>

<head>
<title>モンテカルロ重合シミュレーション</title>

<meta http-equiv="content-type" content="text/html; charset=utf-8">
</head>

<body>

<input type="button" value="どの箱に何個?" onclick="GetRandomNumber2();">


箱1： <span id="sample1">0</span><br>
箱2： <span id="sample2">0</span><br>
箱3： <span id="sample3">0</span><br>
箱4： <span id="sample4">0</span><br>
箱5： <span id="sample5">0</span><br>
箱6： <span id="sample6">0</span><br>


<script type="text/javascript">
<!--
function GetRandomNumber2() {
  var Hako1=0;
  var Hako2=0;
  var Hako3=0;
  var Hako4=0;
  var Hako5=0;
  var Hako6=0;
  
  var randnum;
  
  for(var i=0;i<60;i++){
    randnum=Math.floor(Math.random()*6)+1  ;
    if(randnum==1){Hako1 +=1;}
    if(randnum==2){Hako2 +=1;}
    if(randnum==3){Hako3 +=1;}
    if(randnum==4){Hako4 +=1;}
    if(randnum==5){Hako5 +=1;}
    if(randnum==6){Hako6 +=1;}
   }
   
   
   document.getElementById("sample1").innerHTML =Hako1;
   document.getElementById("sample2").innerHTML =Hako2;
   document.getElementById("sample3").innerHTML =Hako3;
   document.getElementById("sample4").innerHTML =Hako4;
   document.getElementById("sample5").innerHTML =Hako5;
   document.getElementById("sample6").innerHTML =Hako6;
}
// -->
</script>  

</body>
</html>

現実のポリマー

実際の高分子はモノマーが1000個ぐらいはくっつく。そして、そうしてできた合成高分子は、分子量分布を持つという言い方をする。

さー、それでは最初の部分はどうだろうか？
サイコロは２個使えば2-12の数字がランダムに出る。
3個使えば3-18と多くの乱数を出すことは可能だ。

実際の高分子は何本ぐらいの鎖からできているのだろうか？
モノマーの分子量が100g/molだったとしよう。
これは、100g測りとったら、その中にモノマーが1mol=6*1023 個分子がいるということだ。
つまり、モノマーが1000個くっついているなら分子量は100,000になるので、100Kgのポリマーは 6*1023 本の鎖からできている。100gのポリマーでも6*1020 本の鎖になる。

ちなみに、コップ１杯(180ml)の中には、6*1024 個の水分子がある。 地球全部にある水の量は1.35*1024 mlなので（1.35*6/18）*1047 個の水がある。
コップの水を海にまいて、よくかき混ぜて、コップに水を取る。
180mlを1.35*1024 mlで薄めるので、7.5*1021 倍に薄まる。 そして、コップに180ml（6*1024 個）取ると、800個ぐらい、元のコップにいた水分子が入ることになる。
昔、恐竜のした"おしっこ"に含まれていた水分子は、今飲んでいるPETボトルの水の中に必ず含まれているということだ。

よくかき混ぜよう！

では、重合の時の鎖を増やすことを考えてみよう。とは言ってもモルは多すぎるので少なくする。
例えば鎖100本ぐらいでやってみる。

その時に変数の入れ物を100個用意するのは大変だ。 

  var Hako1=0;
  var Hako2=0;

  var Hako100=0;

そこで、 

  var Hako = new Array(101);

とやってあげる。 すると、Hako[0], Hako[1],,,,,Hako[99], Hako[100] と101個の変数を準備したことになる。(０から始まるので実際に使える番号は定義した値の-1になる。）
こうした変数の取り方を配列という。

6*1023 個の変数を定義して、実際の重合に近いシミュレーションをと思うかもしれない。
その時には、自分のコンピュータがどれだけのメモリーを積んでいるか考えてみよう。
キロ、メガ、ギガ、テラ？ そんなのは
103 , 106 , 109 , 1012 で6*1023 に比べればゴミみたいなものだ。

人間の脳は1000億個のニューロンが平均1万個のシナプスでつながっている。そのシナプス1つに0,1の情報を持たせたら、210,000,000*10,000の情報を持たせることができる。
これは、全宇宙に存在する水素原子の数より多い。
そんな脳をAIが超える、シンギュラリティーなど、ちゃんちゃらおかしい。という先生もいる。

脳が負けるわけないノウ！

まー、そこらへんになると化学者の守備範囲は超えている。
せいぜい、1000000個ぐらいまでにしておいた方が良いと思う。

箱を配列で取ると、次の部分は非常にシンプルになる。
randnumには1から100までの乱数が入る。
Hako[randnum] に入っている数を１増やしてあげるだけになる。

for(var i=0;i<5000;i++){
   randnum=Math.floor(Math.random()*100)+1  ;
   Hako[randnum] +=1;
}

結果の表示は、１行に書くことにする。

"\t"はタブ区切りを入れる。
result変数に、箱の中の値とタブ区切りを次々に加えて行って、それをhtmlの方で表示させる。
この結果はコピーして他のソフトにペーストできる。

var result="";
for(i=1;i<101;i++){
   result += Hako[i]+"\t";
}
document.getElementById("sampleX").innerHTML =result;

最終的には次のような動作をする。 自分で、htmlを改造して同じように動くようにしよう。


答え： 0

100本の鎖を作って平均50個のモノマーをくっつけると、一番短いもので35個、一番長いもので70個のモノマーがくっついていた。これは乱数を使った結果なので、やるたびに結果は変わってしまうが。

さらに、1000本の鎖、10000本の鎖で平均50個のモノマーをくっつけるとどうなるか調べてみよう。

さー、こうして自分でプログラムを書いて、その結果得られたデータは、実際にデータサイエンスをやるときの立派なデータになる。
次回はデータサイエンスを行うための基礎を見ていこう。

　

MAGICIANトップ > 高校生にもわかる化学、薬学系 データサイエンス MAGICIAN-Jr. > 第5回

Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。