

| ホームページ | Pirikaで化学 | ブログ | 業務リスト | お問い合わせ |
| Pirikaで化学トップ | 情報化学+教育 | HSP | 化学全般 |
| 情報化学+教育トップ | 情報化学 | MAGICIAN | MOOC | プログラミング |
| MAGICIANトップ | MAGICIAN-Jr. | MAGICIAN-講義 | 過去の資料 |
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)とネットワーク(Networks)を結びつけて(Associate)いかれる人材です。
2021.7.24
前回、箱を100個用意して、50*100(箱一つには平均50個)のモノマーを、乱数で振り分けてみた。
やり方は、1-100までの乱数を発生させて、その箱にモノマーを入れるを、5000個のモノマーに対して繰り返した。やるたびに答えは変わるけど、一番少ないもので35個、一番多いもので70個のモノマーがくっついていた。
そこで、同じ個数入った箱が何個あるか調べてみよう。
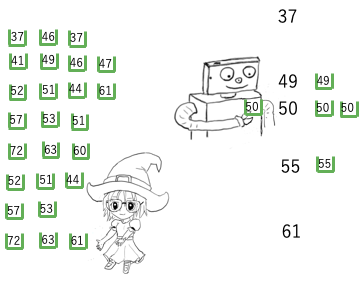
プログラムがどうなっているかの説明は後にして、まず、パラメータを変更せずに"計算する"ボタンをクリックしてみよう。
箱の数がいくつであっても、箱あたりのモノマーの数が50であれば、平均値は50になるはずだ。 ボタンをクリックすると、まず、計算結果が別の画面に表示される。これをCtrl-A, Ctrl-C(マックでは⌘-A, ⌘-C)でコピーして表計算ソフトに貼り付けておく。
そして、このアラートを閉じると、横軸に箱の中身の数、縦軸にその数が入っている箱が何個あったかのグラフが表示される。

このグラフの書き方のプログラムについては、ここでは触れない。
プログラム演習のYMBのところの、逐次反応の結果表示でくわくし説明しているので、そちらを参照してほしい。
箱の中にどれだけモノマーが入るのかは前回説明した。
randnumには1から100までの乱数が入る。
Hako[randnum] に入っている数を1増やしてあげるを繰り返す。
for(var i=0;i<5000;i++){
randnum=Math.floor(Math.random()*100)+1 ;
Hako[randnum] +=1;
}5000回、つまり100個の箱に平均50個繰り返すと、箱の中に何個入ったかは決まる。
そこで、箱の中に30個入っている箱が何個あるか数える。
次は、31個入っている箱が何個あるか数える。
それを繰り返す。
箱の数が、1000個あろうが、10000個あろうが、箱1つあたり50個のモノマーが用意されるので、箱の中身が50個あたりの箱が一番多くなる。
それを積算するプログラムは次のようになる。
例えば、箱の中に50個入っている箱を数えるには、Hako[i]が50だったら、50個箱に入っている変数、NK[50]を1つ増やす、を繰り返す。
Hako[i]が49だったら、49個箱に入っている変数、NK[49]を1つ増やす。
ここは概念的には一番難しいところだろう。
箱にX個入っている箱の数を数える。その結果をNK[X]という変数に入れておく。
時間をとってよく考えよう。
//HakoNum=5000;
//NumKosu=50*2; 平均値50の前後
NK= new Array(NumKosu);
for(var i=0;i<NumKosu;i++){
NK[i]=0;
}
for(var i=1;i<(HakoNum+1);i++){
NK[Hako[i]] += 1;
}箱を何個ぐらいに設定したら、ギタギタが亡くなっただろうか?
100,000個? 1,000,000個?
こんな理想的に乱数を扱う場合でも、最低100,000個のデータが必要なのであれば、データ解析にビッグ・データが必要と騒ぐのも理解できるだろう。
100個の箱の場合と、100,000個の箱の場合で、一箱あたり50個のモノマーを乱数で振り分ける。それぞれの計算結果を、表計算ソフトに貼り付けておく。
100,000個の箱を用意というのは、高分子の鎖を、100,000本用意したということだ。
そして、50*100,000個のモノマーを乱数でくっつけた時に、鎖の長さがどうなっているかを計算してみたということだ。
試しに計算したのが次の図だ。
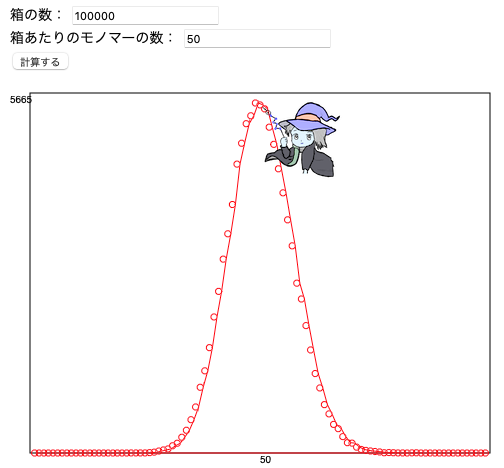
このグラフから、平均50個モノマーがくっついた鎖が5600本/100,000本の鎖あることがわかる。
50個ついたものは、たかだか5.6%だ。
50個もくっつかない、50個以上くっつくものと分布を持っている。
このような、左右対称な綺麗なグラフの形を正規分布という。釣鐘状とも言う。
しかし、正規分布なんて言葉使うから、みんなが統計なんて嫌いになる。
英語で言えば、"Normal Distribution"になる。”普通の分布”だ。
このようなデータがあったときに、まず行う解析は平均値の計算だろう。
最初のギタギタしたグラフが、例えば3クラス、100人の化学の試験の結果だとしよう。
平均を求めるには、35点取った子が何人、36点取った子が何人というように、点数x人数の総和を取る。それを人数で割ったものが平均点になる。
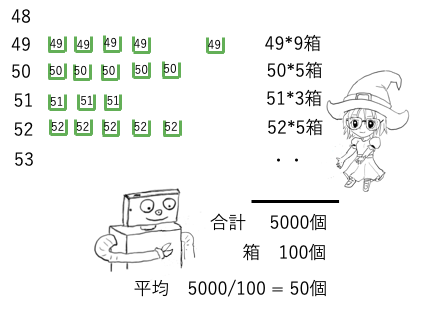
100,000人が受けた全国試験でもやり方は同じだ。
見かけのグラフはとても違うのに、平均値はどちらも同じで50になる。
それでは、このようなデータがあった時に、データはどのようにばらついていると言えるだろうか?
ばらつくという意味は何だろう?
完全にランダム(無作為)であったら、平均50であるはずだ。
だから、ばらつくのは、平均値より大きくなったり、小さくなったりとばらつくことになる。
そのばらつきの大きさは、箱の中の個数とかテストの点の平均からの差になる。
箱の中の個数とかテストの点が48だったら、平均との差は2なのであまりばらついていない。
箱の中の個数とかテストの点が30だったら、平均との差は20なので大きくばらついている。
そのばらつきの平均を取る。
ただし、ばらつきを計算する時に、
箱の中の個数とかテストの点 - 平均値
としてしまうと箱の中の個数とかテストの点が小さい時には値がマイナス、大きい時はプラスになり、それのばらつきを全部足すとゼロになってしまう。
そこで、
箱の中の個数とかテストの点が平均値より小さい時:
平均値 ー 箱の中の個数とかテストの点
箱の中の個数とかテストの点が平均値より大きい時:
箱の中の個数とかテストの点 - 平均値
としてあげる。
つまり平均値からの長さを足し合わせてあげる。長さはマイナスにはならない。
そして、個数で割って平均長さにしたものが、平均のばらつきにになる。
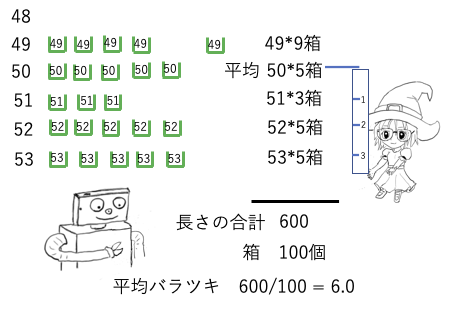
数学的に言えば、ばらつきの絶対値の総和をとって平均値を計算したことになる。
(統計的には、絶対偏差とか平均偏差というが、こんなのは覚えなくても良い。)
表計算ソフトにペーストしておいたものから、実際に計算してみよう。
僕の例では、100個の箱の場合、6.0となり、100,000個の箱の場合5.63になった。
100個の箱の方がばらつきが大きいと言える。
統計学ではバラツキを表すのに分散を使う。
分散というのは平方和の平均になる。
平方和というのは、先程の”平均値からの長さ”の2乗(正方形の面積)を足し合わせたものだ。
何故2乗するかというと、2乗せずに足し合わせると、答えがゼロになるからだと説明する。
(しかし、それなら絶対値を足せば良いだけで、何の説明にもなっていない。 )
そして、標準偏差は、分散のルートをとったものと定義する。
(何故ルートを取るのかというと、先ほど2乗したからだという。どちらもやめれば良い。昔、会社に昼休みに体重減らすためにランニングしてその後アイスを食べている奴がいた。)
実際に計算してみると、
100個の箱の時、分散は54.3、標準偏差は7.37になる。
100,000個の箱の時で、分散は50.0、標準偏差は7.07になる。
100個の箱の場合、平均長さ6.0
100,000個の箱の場合、平均長さ5.63
どちらで見ても100個の箱の方がバラツキが大きい。
それなら、何故、統計学はワザワザ話を難しくするのだろうか?
それは、平均、分散、標準偏差、偏差値などを使うと、様々な先人の叡智が使えるからだ。
例えば、平均±標準偏差の間には、約68%のデータが存在するとかだ。
ただし、それが成り立つのは、分布が正規分布の時だけだ。
例えば、箱の中に50個以上入っている場合には、4つ加えることにしたやり方で計算してみよう。
プログラム的には次のように変更する。(iが最後の一つだとトータル数が狂うかもしれないが)
for(var i=0;i<(NumMon*HakoNum);i++){
randnum=Math.floor(Math.random()*HakoNum)+1 ;
Hako[randnum] += 1;
if(Hako[randnum]>=NumMon){
Hako[randnum] = Hako[randnum]+3;
i=i+3;
}
}平均値は50のままだが、分散は217.3、標準偏差は14.74とバラツキは大きくなる。
しかし、正規分布では無いので、平均±標準偏差の間には、約78%のデータが存在する。
他の統計諸量も意味がないので、統計的に計算しても無駄になる。
平均バラツキ長さ(平均絶対偏差)が10.7だからさっきよりもバラツイていると言っても何の問題もない。
化学の現象はどこまで正規分布に従うのだろうか? 例えば重合などでは、分子量が高くなるにつれ、急にモノマーがたくさんクッツキ始める籠効果というのが知られている。そこで分子量分布が広くなる。大きいものに4つ付けたのはこのことに相当する。
放射性元素の崩壊などは完全ランダムであるが、完全ランダムは非常に少ない。
というか、ほっておくとランダムになってしまうのを、触媒とか使って偏らせたいのが化学ではないかと僕は思っている。
アミノ酸は光学異性体という、L体とD体が存在する。自然界にはL体しか存在しない。
人間が合成すると、L体とD体が半々できてしまう。触媒を工夫して少しでも多くL体を作りたい。
特許というのは、普通こうやったらこんなものしかできないけど、何かを工夫することによってこんなに良くなった。を見つけたから権利をもらう。正規分布から外れた所を狙わなければ特許にはならない。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。