

| ホームページ | Pirikaで化学 | ブログ | 業務リスト | お問い合わせ |
| Pirikaで化学トップ | 情報化学+教育 | HSP | 化学全般 |
| 情報化学+教育トップ | 情報化学 | MAGICIAN | MOOC | プログラミング |
| MAGICIANトップ | MAGICIAN-Jr. | MAGICIAN-講義 | 過去の資料 |
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)とネットワーク(Networks)を結びつけて(Associate)いかれる人材です。
2021.7.30
例えば次のような問題が焼き鳥屋に貼ってあったとしよう。
| 焼き鳥とネギマを合わせて20本買いました。値段は768円でした。ネギマは何本買ったでしょう? |

ネギマは何本買ったかすぐ計算してね。
|
これは小学生の問題なので、連立方程式なんて難しいものを使ってはいけない。+,-,*,/だけの算数を使って解く。
これは、小学生が6年ぐらいで習う、鶴亀算というものを使ってとく。
頭数と足の数だけわかっていて、鶴は足が2本、亀は足が4本として、亀の頭数を求めなさいというやつだ。
これは、実は連立方程式を習ってしまうと、連立方程式を使わずに解くのは先生でも難しいと感じてしまう。
|
答え: まず、20本が全部焼き鳥だったとすると、36円*20本=720円になる。 実際に払ったのは、768円なので48円多く払っている。ネギマは焼き鳥よりも6円高いので、48/6=8本買ったことがわかる。 芸術的だとは思うけど、レバー、つくね、皮と増えて来たら気が狂う。 |

ごめんなさい。連立方程式覚えます--。
|
これは、焼き鳥をx本、ネギマをy本買ったとして、
x +y =20
36*x +42*y=768
を解く。y=20-xとして2番目の式に代入すれば良い。
変数が増えてきたときには、変数消去法を使う。
これは、先程の鶴亀算に近いけど、最初の式の両辺を36倍する。
36x +36y=20*36
これを2番目の式から引けばxを消去できる。

全部計算しちゃえばいい!
|
コンピュータでやるなら、表を使うのも良い。 そして、エクセルとかを使うのであれば、行列を解いて簡単に答えを出してくれる。 |
同じように、自由な組み合わせの焼き鳥の値段も連立方程式を作れば簡単に計算することができる。
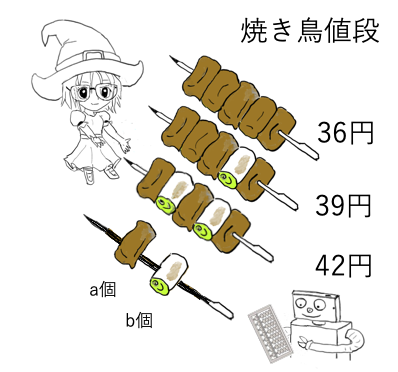
鶏肉の数をx、ネギの数をyとして、連立方程式を作ればいい。
|
5*x=36 4*x + y=39 3*x + 2*y=42 1番目の式からxはすぐわかる。 そのxを2番目の式に入れればyはすぐに求まる。 |
第3回のニューラルネットワークのところでも書いたが、分子を次のように説明することができる。
|
昔、私の子供が一番理解できなかったのが、原子がくっついて分子になる所だ。
焼き鳥を例にして、この鶏肉が炭素、このネギが酸素で串を刺すと分子になる。と一生懸命ビール片手に説明したが結局息子二人とも化学は絶望的にダメだった。 だから、この説明がわからなくても大丈夫。 きっと生きて行かれる。(といいなー) |

お肉は炭素、ネギは酸素。串に刺すと分子。バラバラにしたら原子。
|
この焼き鳥の値段というのは、実は化合物の沸点だ。
CH3-CH2CH2CH2CH3 沸点36℃
CH3-O-CH2CH2CH3 沸点39℃
CH3-O-CH2-O-CH3 沸点42℃
つまり、連立方程式の解は、炭素や酸素一つあたりどれだけ沸点を高くするかを計算したことになる。様々な物性値を計算する原子団寄与法による連立方程式が解かれている。
焼き鳥の場合には、水素の数が入っていなかった。これは、焼き鳥のタレのようなものだ。
真ん中の肉には余りタレはついていない(Hは2つ)けど、両端の肉にはタレが一杯(Hが3つ)付いている。
xは炭素の個数、yは水素の個数、zは酸素の個数、ついでに窒素の個数はwにしてみる。
いきなり燃焼熱を計算するのは何だから、まずは分子量の計算を練習してみよう。
通常、分子の分子量を計算するときは、炭素の原子量12, 水素の原子量1, 酸素の原子量16, 窒素の原子量14を使って、例えばブタン(CH3CH2CH2CH3=C4H10は4*12+10*1で分子量58と計算する。
データサイエンス的には、あらかじめ原子の原子量がわかっている必要はない。例えば、ブタン・ガスの1molを測定したら58gであるという実験値が揃っていれば良い。
| 化合物 | 分子量 | C | H | O | N |
|---|---|---|---|---|---|
| ナフタレン | 128 | 10 | 8 | 0 | 0 |
| オクタン | 114 | 8 | 18 | 0 | 0 |
| ジエチルエーテル | 74 | 4 | 10 | 1 | 0 |
| アンモニア | 17 | 0 | 3 | 0 | 1 |
| メチルアルコール | 32 | 1 | 4 | 1 | 0 |
| エチルアルコール | 46 | 2 | 6 | 1 | 0 |
| メタン | 16 | 1 | 4 | 0 | 0 |
| エタン | 30 | 2 | 6 | 0 | 0 |
| プロパン | 44 | 3 | 8 | 0 | 0 |
| ブタン | 58 | 4 | 10 | 0 | 0 |
| ペンタン | 72 | 5 | 12 | 0 | 0 |
| ヘキサン | 86 | 6 | 14 | 0 | 0 |
| エチレン | 28 | 2 | 4 | 0 | 0 |
| アセチレン | 26 | 2 | 2 | 0 | 0 |
| ベンゼン | 78 | 6 | 6 | 0 | 0 |
| 水素 | 2 | 0 | 2 | 0 | 0 |
| 一酸化炭素 | 28 | 1 | 0 | 1 | 0 |
各構造がどんなものだかわからなければ、ネットで調べてみよう。
それでは、Gauss-Seidelの掃き出し法で、原子量を求めてみよう。
この場合は変数は、C,H,O,Nの4変数なので、方程式はテーブルの上から4つを使う。
求める式は
分子量=X(1) *C個数 + X(2) *H個数 + X(3) *O個数 + X(4) *N個数
を満足する、X(1) , X(2) , X(3) , X(4) を求める。
まずは、プログラムを動かしてみよう。
計算ボタンを押すと、エラー表示も出るが、無事に計算される。 X(1)=12 , X(2)=1 , X(3)=16 , X(4)=14と求まる。

順番にお掃除、お掃除
|
連立方程式は次のようになる。 X(1) *10 + X(2) *8 + X(3) *0 + X(4) *0=128 X(1) *8 + X(2) *18 + X(3) *0 + X(4) *0=114 X(1) *4 + X(2) *10 + X(3) *1 + X(4) *0=74 X(1) *0 + X(2) *3 + X(3) *0 + X(4) *1=17 |
最初の式は次のように変形できる。
X(1) =(128 - X(2) *8 - X(3) *0 - X(4) *0)/10
このとき、X(2), X(3), X(4)の値は0と仮に置く。
X(1)=128/10=12.8になる。
2番目の式は次のように変形できる。
X(2) = (114 - X(1) *8 - X(3) *0 - X(4) *0)/18
この時、X(1)=12.8と掃き出された値を使う。X(3), X(4)の値は0と仮に置く。
X(2)=0.6444になる。
3番目の式は次のように変形できる。
X(3) =(74 - X(1) *4 - X(2) *10 - X(4) *0)/1
この時、X(1)=12.8, X(2)=0.6444と掃き出された値を使う。X(4)の値は0と仮に置く。
4番目の式は次のように変形できる。
X(4)=(17 - X(1) *0 - X(2) *3 - X(3) *0)/1
X(1), X(2), X(3)の値は掃き出された値を使う。
後は、また1番目の式に戻り、今度は、X(2), X(3), X(4)の値は1サイクル目で求めたものを使いながら順番に更新していく。
値が変わらなくなったら終了する。
将来は、Rを使う、Pythonを使うなどで、コンピュータにお任せで原理を考える事は無くなるだろう。
中学で習う連立方程式が基本なので、思い出す最後のチャンスになる。
全く同じことなので燃焼熱は自分でやってみよう。データは次のようになる。やはり最初の4つを使えば答えが求まる。
| 化合物 | 燃焼熱 KJ/mol | C | H | O | N |
|---|---|---|---|---|---|
| ナフタレン | 5149 | 10 | 8 | 0 | 0 |
| オクタン | 5501 | 8 | 18 | 0 | 0 |
| ジエチルエーテル | 2725 | 4 | 10 | 1 | 0 |
| アンモニア | 380 | 0 | 3 | 0 | 1 |
| メチルアルコール | 744 | 1 | 4 | 1 | 0 |
| エチルアルコール | 1365 | 2 | 6 | 1 | 0 |
| メタン | 888 | 1 | 4 | 0 | 0 |
| エタン | 1556 | 2 | 6 | 0 | 0 |
| プロパン | 2215 | 3 | 8 | 0 | 0 |
| ブタン | 2859 | 4 | 10 | 0 | 0 |
| ペンタン | 3513 | 5 | 12 | 0 | 0 |
| ヘキサン | 4174 | 6 | 14 | 0 | 0 |
| エチレン | 1408 | 2 | 4 | 0 | 0 |
| アセチレン | 1298 | 2 | 2 | 0 | 0 |
| ベンゼン | 3297 | 6 | 6 | 0 | 0 |
| 水素 | 284 | 0 | 2 | 0 | 0 |
| 一酸化炭素 | 284 | 1 | 0 | 1 | 0 |
htmlの計算ボタンの部分は次のようになる。
<input type="button" value="掃き出し計算" onclick="GaussSeidel();"><br>
掃き出し法: <br><span id="sample">***</span>Javascriptの部分は次のようになる。
<script type="text/javascript">
<!--
//掃き出し法ではNData=NDescになる。
var NData = 4+1;//タイトル行の分1を足す
var NDesc=4+1;//化合物名の列の分1を足す
//MWのところに燃焼熱を入れる。
var MyData=
[
["name","MW","C","H","O","N"],
["ナフタレン",128,10,8,0,0],
["オクタン",114,8,18,0,0],
["ジエチルエーテル",74,4,10,1,0],
["アンモニア",17,0,3,0,1]
];
var A =new Array(NData);
for(var i=0;i<NData;i++){
A[i]=new Array(NDesc);
}
var B =new Array(NData);
var W =new Array(NData);
var Iter=1000;
var X=new Array(NDesc);
var Result="";
var ANORM=0.0;
var XNORM=0.0;
function ReadData(){
for(var i=1;i<NData;i++){
for(var j=1;j<NDesc;j++){
A[i][j]=parseInt(MyData[i][j+1]);
}
B[i]=parseFloat(MyData[i][1]);
}
}//Read
function GaussSeidel(){
ReadData();
for(var i=1;i<NData;i++){
var Sum=0.0;
for(var j=1;j<NDesc;j++){
if(i!=j){
Sum=Sum+Math.abs(A[i][j]);
}
}// line 10
if(Math.abs(A[i][i])<=Sum){
Result="エラー:Aiiの絶対値は、i!=jのAijの絶対値の和よりも大きい必要がある。"+"<br>";
//document.getElementById("sample").innerHTML = Result;
//return;
}
}
for(var i=1;i<NDesc;i++){
X[i]=0.0;
}
Result +="ITER"+"\t";
for(var i=1;i<NDesc;i++){
Result += "X("+i+")\t";
}
Result +="<br>";
for(var ii=1;ii<Iter;ii++){//Iter=1000
ANORM =0.0;
XNORM =0.0;
for(var i=1;i<NData;i++){// i番目の方程式
//X[i]を決定する。
var W=B[i];
for(var j=1;j<NDesc;j++){//i以外を右辺に掃き出す
if(i!=j){
W = W - A[i][j] * X[j];
}
}
W=W/A[i][i];//方程式の順番。i番目の方程式はA[i][i]は0ではダメ。なるべく大きな値
ANORM = ANORM + Math.abs(X[i] - W);
XNORM = XNORM + Math.abs(W);
X[i] = W;
}
//結果の表示
Result += ""+ii+"\t";
for(var i=1;i<NDesc;i++){
Result += ""+Math.round(X[i]*1000)/1000+"\t";
}
Result +="<br>";
if(ANORM / XNORM < 1E-05)break;
}//ITer
document.getElementById("sample").innerHTML = Result;
}
// -->
</script>連立方程式の解法を敢えて説明したが、将来はソフトを使って解くだけになるだろう。
エクセルのツール/データ分析/回帰分析 を行えば、簡単にX(i)の係数を求めてくれる。
これも逆行列を解いているのだろう。
ただし、計算が失敗することもある。その時には連立方程式に戻って検討してみよう。
| CH3 | CH | Boiling Point (K) |
|---|---|---|
| 2 | 0 | 184.5 |
| 3 | 1 | 261.3 |
| 4 | 2 | 331.2 |
| 5 | 3 | 386.6 |
例えば、このような沸点のテーブルを解析してみる。
2行目の方程式を2倍して3行目の方程式を引くと、CH3は2個で、CHは0個だが、1行めとCH3ひとつあたりの沸点が異なる。
2行目の方程式を3倍して4行目の方程式を引くと、CH3は4個で、CHは0個だが、1行めとCH3ひとつあたりの沸点が異なる。
何故係数が不定になるか、連立方程式に戻れば、このようにはっきり分かる。
難しい言い方をすると、CH3とCHの列が共線性関係にあるので解が不定になるという言い方をする。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。