

| ホームページ | Pirikaで化学 | ブログ | 業務リスト | お問い合わせ |
| Pirikaで化学トップ | 情報化学+教育 | HSP | 化学全般 |
| 情報化学+教育トップ | 情報化学 | MAGICIAN | MOOC | プログラミング |
2012.1.12
化学工学の本を見ると、抽出操作の部分は3成分の溶解度平衡のデータからタイラインを引いて、うんたら、かんたらと説明されています。
20年近く前の”マイコンを使ったXXXX”という類いの本、最近の”Excelを使ったXXXXX"といった類いの本も変わりません。
Pirikaでは20年以上前からJAVAを使って化学用のプログラムを提供してきましたが、この抽出操作に関しては何も提供できませんでした。
その理由はプログラムが書けないからではありません。
3成分系の溶解度平衡のデータが、全く増えていかず、いつも、水-ベンゼン-酢酸などのデータを延々と使い続けています。 (もうベンゼンなんて使うはずないのに)
それでは任意の3成分系の溶解度平衡を推算できるかというと、それはできません。そこでプログラムを作る価値がなかっただけです。
しかし、化学の領域の研究をするのであれば抽出は重要な操作です。
医薬品などのように分子のサイズが大きくなってくると、蒸留で副生成物を分けるのは難しくなります。
熱安定性の低い化合物の分離にも抽出は欠かせません。
ある化合物をある溶媒(水である事が多い)から抽出するときに、どんな溶媒がいいか? に対してどのような提案ができるでしょうか?
YMBを使って検討してみましょう。
ここでいう抽出は分液ロートを使ってしゃかしゃか振った時をイメージしてください。
課題:
化学便覧に以下の化合物の分配係数が記載されています。
各化合物をYMBを使って計算しましょう。
分配係数データ
抽出に使った溶媒は、1-オクタノール、ジエチルエーテル、クロロホルム、四塩化炭素、ベンゼン、ヘキサン(ヘプタン)です。このうち、水と1-オクタノールの分配係数はlogKow, logPなどとも呼ばれる指標でYMBの中に推算値が記載されています。
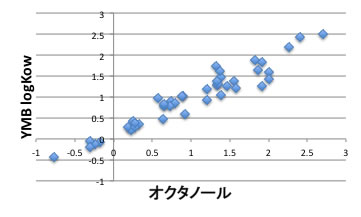
YMBの計算結果と化学便覧のデータとプロットすると上図に示すように非常に良好に推算できている事が分かります。
つまり、1-オクタノールを抽出溶媒に使う限りは、ある任意の溶質がどれだけ水に、どれだけ1-オクタノールに分配しているかはYMBで計算すれば分かることを意味しています。
自分が抽出したいものが1-オクタノールに多く分配していればそれでOKですが、そうで無かったらどうやって抽出溶媒を選択したらいいでしょうか?
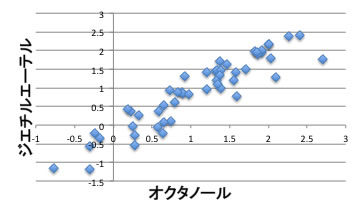
ジエチルエーテルとオクタノールの分配係数をプロットしてみると、かなり高い相関がある事がわかります。
従って抽出溶媒として1-オクタノールで不十分であったのなら、ジエチルエーテルに変えてもあまりいい事はないでしょう。
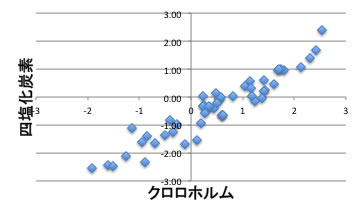
同様にクロロホルムと四塩化炭素の分配係数も、当たり前の事ながら非常に高い相関があります。
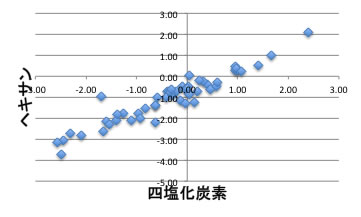
そして、意外な事にヘキサンと四塩化炭素の分配係数には非常に高い相関があります。
ベンゼンとヘキサンの相関係数はあまり高くありません。
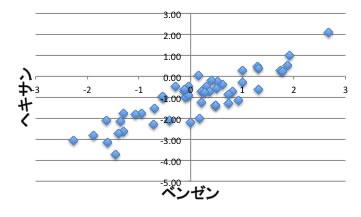
従って、化学便覧にデータのある、1-オクタノール、ジエチルエーテル、クロロホルム、四塩化炭素、ベンゼン、ヘキサンは、3つにグループ分けして考えればいい事が分かります。
いわゆる極性溶媒は水に溶解してしまうので、水系の抽出溶媒には用いる事ができません。
先に述べたように、1-オクタノールの分配係数は分子構造のみからYMBで推算することができます。
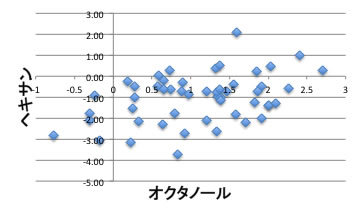
オクタノールとヘキサンでは極性がずいぶん異なるので上図に示すように相関が無ありません。
そこで、YMBとYSBを使ってヘキサンの分配係数を推算するモデル式を作ってしまうことを考えます。
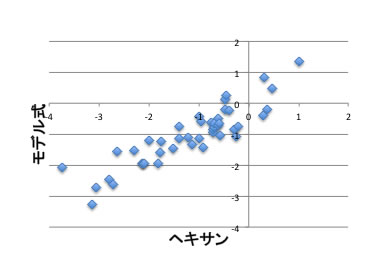
課題: YSBを使って下のモデル式のA-Eの係数を定めてみましょう。
ヘキサン分配係数モデル式=A*logKow +B*Surface Area C*Ovality D*Density +E
こうしたモデル式が作製できると、ヘキサンとオクタノールで分配係数がどういう関係になっているか定量的に理解することがきます。
つまり、ある抽出したい溶質があったときに、YMBを使えばlogKowは推算できます。
こうしたことを、このモデル式は示しています。
課題: 同様に、ジエチルエーテル、クロロホルム、四塩化炭素、ベンゼンの分配係数をlogKowをベースに組んでみよう。
これらのモデル式が構築できると、あるターゲットの化合物を抽出する溶媒は、中間(極性に近い)、中間(非極性に近い)、非極性のどのくらいがいいか明確にわかるようになります。
AIにどのように分配係数を教えるかはともかく、優秀な人間の研究者は、ベースとなるlogKowを知れば、他の抽出溶媒を使ったときの傾向は見当がつきます。
それは、絶対的な
辛いのはどれでしょう?
唐辛子の赤色はパプリカ色素として、食品の着色に使われます。
色素にカプサイシンが残ると辛いです。
色素は加熱すると変色します。
そのようなものは超臨界二酸化炭素で抽出するという手が使えます。

(株)ILSHINオートクレーブのホームページにどうのようなものに適用できるかよくまとまっています。
しかしこれだけでは、どのような構造のものが、定量的にどれだけ抽出できるかは分かりません。
この定量性に注目して超臨界二酸化炭素抽出を見てみましょう。
東北大学多元物質科学研究所が理論計算の結果と溶解性をQSARした結果を、熱物性 21 No3(2007) p137-142に投稿しています。
分極率指数、分子軌道の塩基性度、静電的塩基性度、静電的酸性度から溶解性を推算する式を構築しています。
この方法は、最近のMaterials Informaticsの走りのようなやり方です。
分子軌道法を使えば、どんな化合物でも計算できます。
そして、溶解度という目的変数に対して、説明変数を用意することができます。
目的変数と説明変数の関係をDeep Learningすれば中身はブラックボックスでも予測モデルを作ることができます。
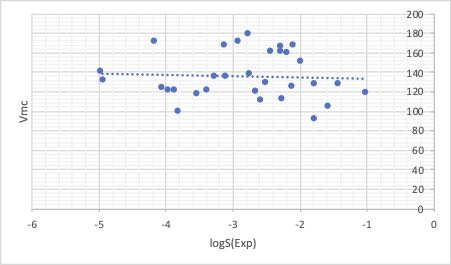
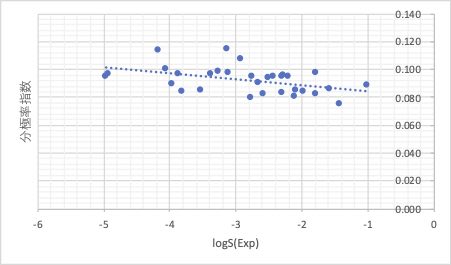
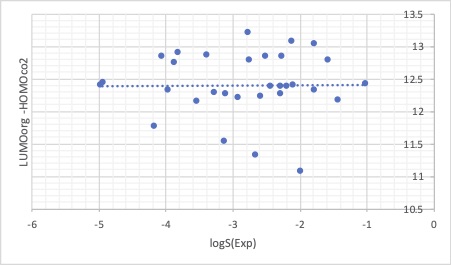
実際に大学の特許をトレースしてみてもMOの計算値と溶解性の間には明確な相関はありません。
多くの論文でマテリアルズ ・インフォマティクス を分子軌道法と組み合わせてやっているのを見かけます。
しかし、こうした各々に相関の無いものを組み合わせてモデルを作った場合には、データが増えてくると合わないものが出て来ます。そしてモデルを作り直す、の繰り返しになります。
ここでは、YMBで計算してみましょう。
下記のデータにあるSmilesの構造式を使ってYMBの計算値をまとめてください。
超臨界抽出データ
YSBで変数選択を行うと、必ず融点を変数の一つに選択します。
それは下図に示すように融点と溶解度が非常に高い相関を持っているからです。融点は熱振動が分子間力に打ち勝って液体になる温度ですので、超臨界CO2の運動エネルギーが勝った場合に溶けると考えると合理的な気がします。
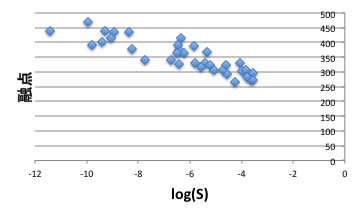
しかし、それが正しいとしますと、カプサイシンの溶解度は-19.48となり、ほとんど溶解しない事になり現実と合いません。そこで融点のカラムを消去し変数選択を行います。
選択する変数の数を変えたり系列の種類を変えたりしながら複数のモデル式を作ってみましょう。
(例えば、HSP関連の説明変数だけから作る。臨界定数絡みで作る。logKowや関連の説明変数から作る。)
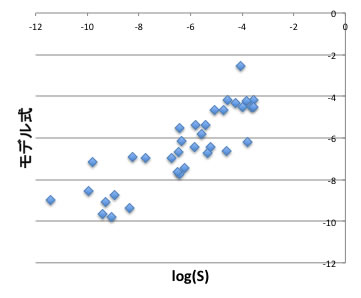
一例ととして、
モデル式= A*密度 +B*HansendD -C*表面張力 -D
YSBを用いてA-Dの変数を求めてみましょう。
このモデル式を用いてカプサイシンを計算すると、-4.84となり一連の化合物の中でも非常に高い抽出となる事が予測される。
密度に関してはPirikaのこちらの記事を参照の事。
表面張力に関してはPirikaのこちらの記事を参照の事
対応するブラウザーを使い、上のキャンバスに分子を描けばどのくらいの溶解度かを得る事ができます。 詳しい分子の描き方はこちらを参照してください。
このように、一旦モデル式が作成できれば容易に新しい溶質を使った時の溶解度を推算できるようになります。
しかし、コンピュータだけに頼らず”何故”を考えるのは非常に重要です。
このモデル式の中で一番寄与の高いのが表面張力です。
表面張力と溶解度をプロットしてみましょう。
YSBの変数選択は相関係数の高さに注目して行われるので、注意が必要です。
特に今回の融点は自分も危うくだまされる所でした。逆に言えばYMBの出す答えが何故、相関係数が高いのかを考える事は新しい閃きに通じる事もああります。
こうして得られたモデル式は、複雑な理論計算した式と比べても遜色無いものでした。
さらにデータを拡充して検討を加えた所、この表面張力が溶解性をコントロールしているその本質は、マランゴニ対流ではないか? と考えています。(2013.8.21)
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。