

| ホームページ | Pirikaで化学 | ブログ | 業務リスト | お問い合わせ |
| Pirikaで化学トップ | 情報化学+教育 | HSP | 化学全般 |
| 情報化学+教育トップ | 情報化学 | MAGICIAN | MOOC | プログラミング |
2014.7.17(2020.4.27改訂)
計算関係で会社に入ったら一番に役に立つのが、重回帰計算法でしょう。Excelにも搭載されているので使い方は完全にマスターしておきましょう。
例えば、八百屋で果物の詰め合わせが売っています。
| ケース | 値段 | みかん | りんご | ばなな |
| 1 | 300 | 2 | 2 | 0 |
| 2 | 180 | 3 | 0 | 1 |
| 3 | 360 | 4 | 1 | 2 |
| 4 | 180 | 1 | 1 | 1 |
| 5 | 350 | 3 | 2 | 0 |
| 6 | 460 | 4 | 2 | 2 |
| 7 | 520 | 2 | 3 | 4 |
| 8 | 440 | 3 | 2 | 3 |
みかん、りんご、バナナの値段はいくらでしょう?
という問題があったとします。これは連立方程式の問題で、中学生ぐらいで習うと思います。
暗算でも簡単に解けるでしょう。
YSB-YNU20を使ってデータを入れれば簡単に結果が得られます。
Input Dataのテキストエリア にタブ区切りのデータをペーストします。
Readボタンをクリックしてデータを読み込みます。
Cross Term MR式を選択してBuildしてみましょう。
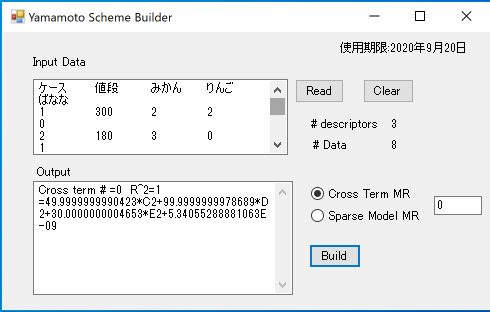
YSB-YNU20が見つけた答えは次のようになります。
=49.9999999990423*C2+99.9999999978689*D2+30.0000000004653*E2+5.34055288881063E-09
この式を表計算ソフトのF2にペーストしてみましょう。
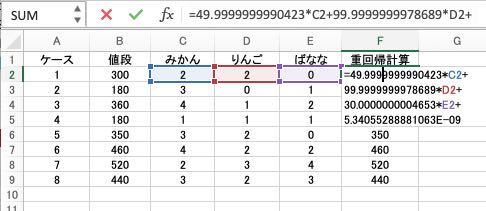
式の中の、C2, D2, E2は表計算ソフトのC列(みかん)、D列(りんご)、E列(バナナ)の2行目(ケース1)の果物の個数をを表しています。
つまりYSB-YNU20の構築した式は表計算ソフトの2行目を計算する式になります。
(元データと重ならなければ、列はどこにペーストしてもよいです。)
後はその式を広げていけば全てのケースが埋まります。
細かい小数点以下の係数はともかく、
値段=50*みかん個数+100*りんご個数+30*バナナ本数
という式で、目的変数(値段)を説明変数(各くだものの個数)で表した推算式が構築できたと言うことです。
一般にある目的変数が1つあって、説明変数が複数あるときに、上のような式を得る事を重回帰解析といいます。
各説明変数の前にある50, 100, 30を重回帰係数と呼び、式自体を重回帰式と呼びます。
こうした重回帰式は化学の分野でもよく使われ、例えば沸点の推算のJoback法では原子団の数とその寄与度から次式で沸点を推算します。
\[T_b=198.2+Σ(n_i * Δb_i)\]
\[T_b: 標準沸点,[K]\]
\[n_i: i番目の部分構造の数\]
\[Δb_i: JOBACKのi番目の部分構造の沸点に対する寄与度, [K]\]
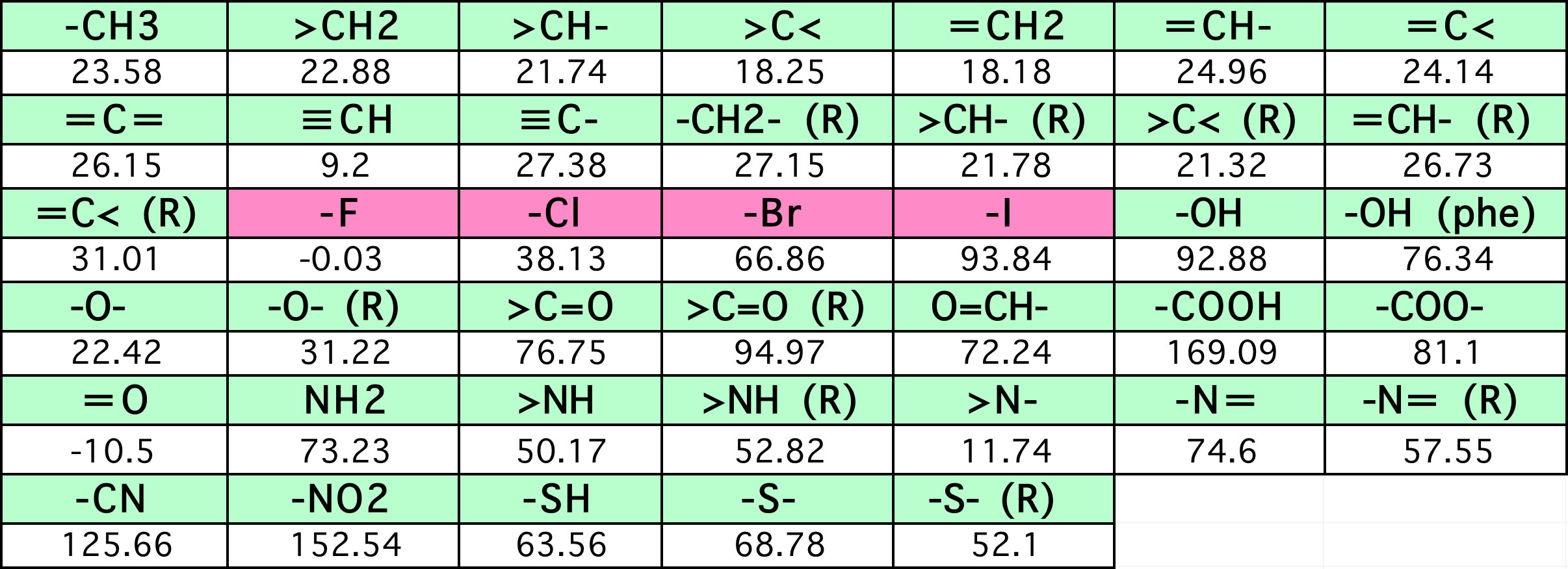
例えば、エタノール(CH3-CH2-OH)の沸点を求めたかったら、
Tb=198.2 + 23.58*1(CH3) + 22.88*1(CH2) + 92.88*1(OH) = 337.54 K = 64.39℃
のように求めます。
この重回帰の係数は何を意味しているのでしょうか?
果物の値段と同じで、分子中にOH(水酸基:92.88)が1つ入った場合には、CH2基(22.88)4個分ぐらい沸点が高くなることを示しています。
こうしたやり方は、原子団寄与法と呼ばれ、いろいろな推算式が提案されています。
そうした推算式を構築したければ、物性値と「原子団が幾つあるか」のテーブルを作成し、表計算ソフトに搭載されている重回帰計算を行えば推算式が構築できます。
最初から分子構造と原子団の数の対応表を作ってしまえば、Smilesの構造式から解析する必要は要らなくなります。しかし、原子団の切り方を変更したり、ユーザーが間違って原子団を分割したりすると思いもよらない推算結果になってしまいます。そこでYMB-YNU20では原子団の切り方はプログラムによって制御されています。
ここまでの計算であるなら、Excelのデータ分析ツールの回帰分析で計算ができます。
ただし、算数ならともかく、化学の現象はそこまでシンプルでは無い事が多いのです。例えば温度が上がると急に反応速度が早くなったり(非線形性)、ある圧力とpHで急に様子が変わったり(相互作用)一筋縄ではいかない事が多いのです。
難しい例として水への溶解度の推算した例を解説していますので、一読する事をお勧めします。
難しい題材の時は、QSPR(定量的構造物性相関)の手法として「ニューラルネットワーク法」などを用いて解析を行います。しかし、これはこれで過学習などの問題があり使い方が難しいのです。ニューラルネットワーク法などは情報化学の方で扱います。
例えば、先ほどの例で果物の値段を決める時に、バナナとリンゴは大量入荷したので、バナナとリンゴを両方購入した場合には、X円*バナナ本数*リンゴ個数だけ割引するとしましょう。
テーブルは次のようになります。
| ケース | 値段 | みかん | りんご | ばなな |
| 1 | 300 | 2 | 2 | 0 |
| 2 | 180 | 3 | 0 | 1 |
| 3 | 340 | 4 | 1 | 2 |
| 4 | 170 | 1 | 1 | 1 |
| 5 | 350 | 3 | 2 | 0 |
| 6 | 420 | 4 | 2 | 2 |
| 7 | 400 | 2 | 3 | 4 |
| 8 | 380 | 3 | 2 | 3 |
各果物の値段と、いくら割り引いたかのX円を求めてみましょう。
暗算で解けますか?
この例題は、これまでの授業で何回も使っていますが、暗算で解けた学生はいませんでした。
では、暗算で解けないのはいいとして、
「こういう解き方をすれば、Xが求まる」
という考え方を示してください。
その手のソフトウエアーを使えば、簡単にできます。
しかし、それでは、中学生でも高校生でも誰でも答えを出すことができます。
どうしたら、答えが求まるか、「考える力」を鍛えることなしに、ソフトの使い方だけを覚えるのであれば、すぐにAIに追い抜かれるでしょう。
AIは「覚える力」だけなら人間をとうの昔に追い抜いています。
しっかり大学院生なりに「考えた」として、ソフトの使い方を見て行きましょう。
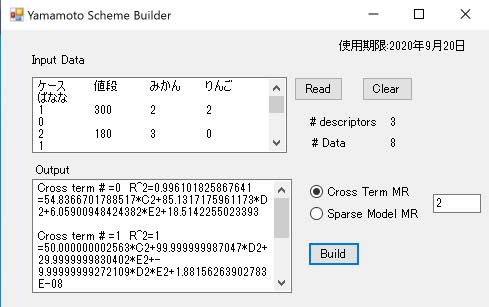
ここでは、Cross Term として2を指定します。すると、YSB-YNU20はクロスタームを0から2まで増やしながら式を構築していきます。
相関係数の2乗(R2 決定係数)は0.9961になります。この値は1に近いほど良いモデルが構築できたことになります。
値段=54.8367*みかん個数+85.1317*リンゴ個数+6.059*バナナ本数+18.5142
となります。
この重回帰式は明らかにおかしいです。何も買わなくても18.5円になってしまいます。
しかし、統計的には決定係数は非常に高く、正しく推算できているように思えてしまいます。
この場合は、実はX=10円としてあります。
こうしたXを求める事は表計算ソフトに付属の重回帰計算ではできません。
しかし、先ほどのJoback法の沸点の推算で、COOHが沸点を上げる効果、NH2が沸点を上げる効果の各々の重回帰係数が求まっていても、COOH,NH2を両方持つ化合物の沸点が各々の重回帰係数の和だけで決まらない事は明らかです。
+X*COOH個数*NH2個数
の補正値を入れないと答えは合いません。
こうした説明変数間の相互作用を考慮し、クロスタームを自動的に挿入するのがYSB-YNU20というソフトウエアーです。
果物の例では、クロスタームは、みかん*りんご、りんご*バナナ、みかん*バナナ、みかん*みかん、りんご*りんご、バナナ*バナナの6種類あります。
その6種類を評価して、決定係数が一番高くなるクロスタームを1つ選択します。(どのクロスタームを選ぶかは、あくまでも決定係数の大きさであることは注意が必要です。)
値段=50*みかん+100*リンゴ+30*バナナ+-10*リンゴ*バナナ+0
という重回帰式を構築してくれます。
そして、その時の決定係数は1になる事が示されています。この場合はとてもシンプルですが、実際の問題への応用は、クロスタームの数と決定係数の値を見ながら最適なクロスターム数を人間が決定する必要があります。Web版のYSB-YNU20はクロスタームに上限があります。
線形式、非線形式をどのように使いこなすかに関しては、ハロメタンのケミカルシフトの記事を参照にしてください。
このように、クロスタームを重回帰式に導入すると、
「みかん*みかん 」のように同じものが選ばれた場合には、2次式になり非線形性が導入されます。
「みかん*りんご 」のように違うものが選ばれた場合には、相互作用項が導入されます。
重回帰法の係数の見通しの良さを保ちつつ、重回帰法の欠点を改良した推算式の構築法になります。
こうした方法が、何故、今まで余り使われなかったのかと言うと、論文や特許にグラフを載せてもたいして違いが無かったからだと思います。
例えば、CTが0の場合。
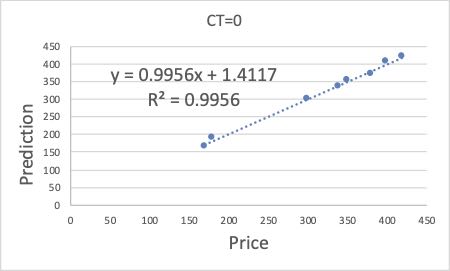
CTが1の場合
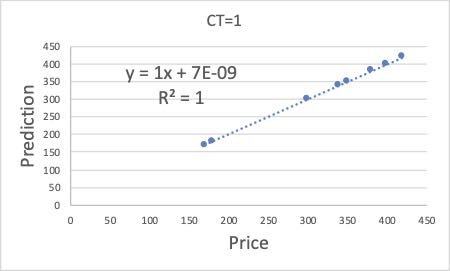
どちらも、良いモデルができているので、CTを入れなくても十分とも言えます。また、実際のモデル構築はここまで綺麗なことは稀で、結果が分かっているからクロスタームを導入できたとも言えます。
しかし、Materials Informaticsなどを使って、物性推算と逆設計を行おうとした時には、何も買わなくても18.5円というモデルを使うと困ったことにもなりかねません。
適度に導入して、逆設計しやすいモデルを作ることは重要です。
非線形性や相互作用項は入れすぎても、入れなさすぎてもダメで、そこが人間が関与しなくてはいけない大事な領域として残っているのだと思います。
YMB-YNU20では20種類以上の物性(学生版のYMSBではさらに多くの)を推算して、それを使ってモデル式を作成します。
実験値の数に比べて、説明変数が多い系を解析するには、主成分分析やPLS法を使うように情報化学では教えてくれます。
しかし、本来必要のない説明変数は、刈り込むのが一番です。
YSB-YNU20には変数選択重回帰法(Sprse Model MR)が搭載されています。この方法について簡単に説明しておきます。
お店で売っている果物の詰め合わせで、400円以上の籠に飾りをつけました。飾りの値段はいくらになるでしょう?
| ケース | 値段 | みかん | りんご | ばなな | Decoration |
| 1 | 300 | 2 | 2 | 0 | 0 |
| 2 | 180 | 3 | 0 | 1 | 0 |
| 3 | 360 | 4 | 1 | 2 | 0 |
| 4 | 180 | 1 | 1 | 1 | 0 |
| 5 | 350 | 3 | 2 | 0 | 0 |
| 6 | 460 | 4 | 2 | 2 | 1 |
| 7 | 520 | 2 | 3 | 4 | 1 |
| 8 | 440 | 3 | 2 | 3 | 1 |
科学で観測しているのは、こうしたテーブルの中身だけです。恣意的に割り引いたり、値段に関係ない飾りをつけたりしてあるかどうかは果物店の店主にしかわかりません。
このくらい単純な系では、普通にクロスターム重回帰をやって結果を見ると、すぐに分かります。
値段=50*C2+100*D2+30*E2+8.3109E-09*F2+1.0227E-08
CT=0でも飾り(F2)の係数は8.3109E-09なので0円になります。
では、バナナとリンゴは大量入荷したので、バナナとリンゴを両方購入した場合には、X円*バナナ本数*リンゴ個数、割引した上で飾りをつけたらどうなるか。さらに説明変数が増えたらどうしたら良いか? 難しい問題になります。
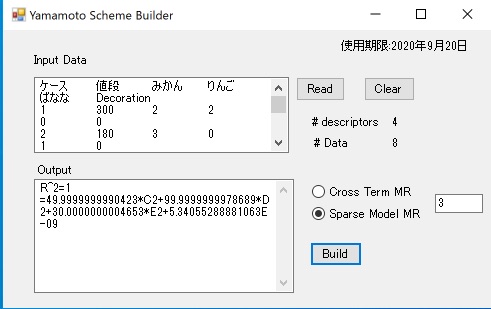
取り敢えず、YSB-YNU20でSpase Model MRを使ってみましょう。3変数を使ってモデルを構築すると、飾り(F2)の値段は使わなくてもモデルが作れる事がわかります。
実用的に威力を発揮するのは、YMB-YNU20で、20種類以上の物性値を使って変数選択する場合です。詳しいことはそちらで説明します。
YSB-YNU20を使ってモデルを構築すると、
* 非線形性や相互作用項を導入する事ができる。
* モデル構築に影響を与えない説明変数を刈り込む事ができる。
この2つの事は覚えておきましょう。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。