Y-MB2021の推算精度

2022.9.8

解析例トップ
　DIYトップページ >
　HSP基礎トップページ >

Y-MBの改良

SMILESの構造式を解析して、HSPや熱力学的物性値を推算するY-MBは2009年3月に発売のHSPiP ver. 2から搭載されている。

その後、延々と改良を重ねている。

あまり昔の話をしてもしょうがないので、HSPiP ver.5　(WIndows 10 用：2015年11月）に搭載されているY-MB2014, HSP50周年記念（2017年）に合わせて作成したY-MB2016。
そして、HSPiPにはまだ搭載されていない、Y-MB2019(コロナ前で最後の対面の開発者会議のあった年）。
2020年に勤めていた会社を定年退職して、開発に専念できるようになり、根本からY-MBを作り直した、Y-MB2021の推算精度の話をしよう。

官能基の種類

ver.5シリーズでは、使える官能基の種類は変更がない。リストを参照してほしい。

HSPの拡張

推算精度の前に、HSP50周年記念講演会で発表した、δDfgについて触れておこう。
詳しくは、山本博志、基調講演-Part1か、予稿集Part 1を参照してほしい。

まとめとして、δDの分割のページを作ったのでそちらを参照してほしい。

簡単に説明すると、1967年のハンセン溶解度パラメータで定義される、δDは２つの成分の足し合わせであると理解する必要がある。

δD² = δDvdw² + δDfg²

1967年当時は、脂肪属炭化水素はδP,δHの値を持たないため、蒸発のエネルギーは全てδDに割り振られていた。

ところが、例えばパーフルオロの化合物もδP,δHの値を持たない。しかし、脂肪属炭化水素とパーフルオロの化合物はHSPがほぼ同じでもお互いに溶解しない。

そこで、分子が大きさを持つだけで必要な蒸発エネルギーを定義する。希ガスやパーフルオロの化合物は分子間の相互作用は分子の大きさだけに支配されていると考える。

それをδD_vdw（ファンデルワールス）分のδDと定義する。
これは全ての分子の大きさが決まった段階で自動的に決まる。

そして、分子の構成要素（原子種、原子団）によって決まるδDfgは、次式で計算される。

δD_fg=sqrt( δD² – δD_vdw²)

このように定義すると、脂肪属炭化水素は大きなδD_fgを持つが、ばパーフルオロ化合物のδD_fgはほぼゼロになる。

HSP距離の式は次のようになる。
Distance₁₉₆₇={4.0*(δD₁-δD₂)² +(δP₁-δP₂)² +(δH₁-δH₂)² }^0.5

Distance₂₀₁₇ = {(δD_vdw1-δD_vdw2)² +(δD_fg1-δD_fg2)² +(δP1-δP2)² +(δH1-δH2)² }^0.5

これまで、とても不思議とされていた、δD項の差分の前にあった4.0というファクターがいらなくなった。

ポリマーを溶解する88溶媒同士の距離を両方の式で計算してみた。

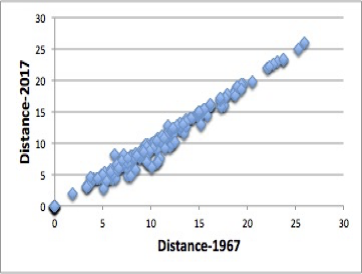
この結果から、 Distance₁₉₆₇のファクター4は要らない事がわかる。

ポリマーの距離の式

HSPiPにあるポリマーの溶解性の例題で、Distance₁₉₆₇とDistance₂₀₁₇を使った場合の、間違って認識される数を調べたところ次のようになった。

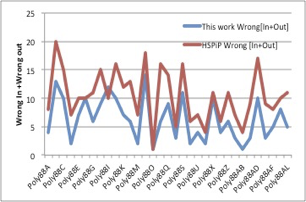
Distance₂₀₁₇の方がほぼ全てのケースで誤認識する数が減った。

そこで、δDfgもきちんと推算できる必要がある。

Y-MB物性推算式の構築

分子の構造を調べて、そのハンセンの溶解度パラメータを推算するのは、とても大変なことだ。単純な原子団寄与法では精度がでない。

それは、ある意味仕方がない。
ハンセン先生が決められたオリジナルの部分は時には論理的ではない。
その先生の恣意的な部分は残しつつ、ユーザーが求める中大分子まで拡張させる。まだ見ぬ複雑な構造であっても計算が破綻しないようにしなければならない。

2017年のHSP50周年に合わせてY-MB2016を作ったが、上のような要請に合わせようとすると、非線形性解析式（ニューラルネットワーク法の亜流）を組むことになる。

しかし、非線形性を上げすぎると、見かけ上のフィティングは良くなるが、外挿の際に破綻する。

物性推算構築用の4Kデータベースがある。（これはモノマネをして、自称する輩がいるので公開していない。）
HSPの予測式もこのデータベースを解析して作成する。

全く非線形性を導入しないで原子団の数だけから重回帰法を使って推算式を構築すると次のようになる。あまり精度がでない。

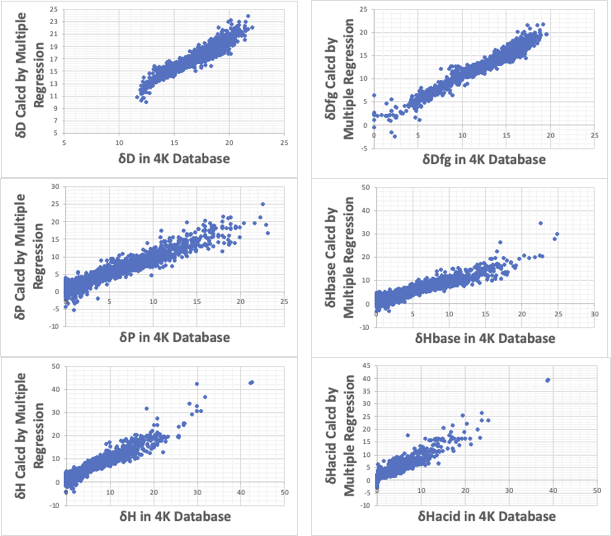
そこで、これまで延々と改良を続けている。

重回帰式では精度が出ないので、原子団以外の構造パラメータを色々加え、さらに非線形を加味した推算式を検討してきた。

δDの予測式

Y-MB2014からY-MB2019までは非線形性の調整を色々行った。
Y-MB2021は非線形性の導入を止め、全く新しい推算アルゴリズムを開発して計算した。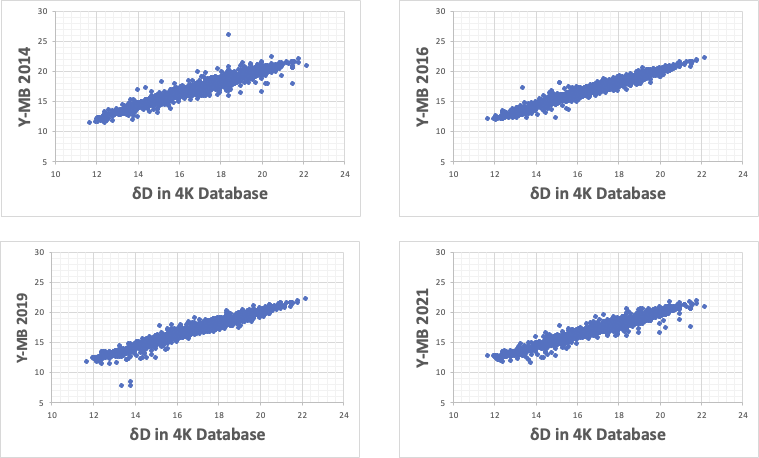




４KDatabaseで、非線形性を調整して得られた式を使い、10KDBの化合物について計算してみる。
10KDBの中には式を構築するのに使った化合物も含まれるが、8000化合物ぐらいについては予測値しかない。

とりあえず、非線形性の無い重回帰計算の結果と比較してみる。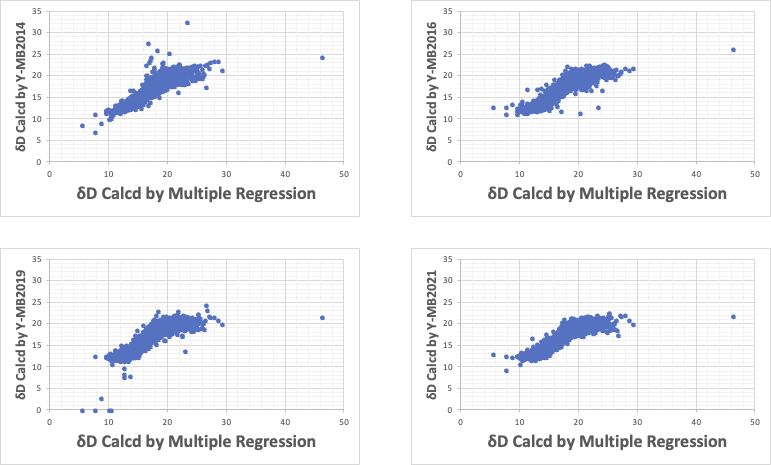



例えば、重回帰法ではδDが40以上になる化合物がある。

これは、δDを大きくするような原子団がとてもたくさん入っているような化合物でこうなる。（もちろん、原子団の体積も関係してくるのでもう少し複雑だが）

しかし、δDを大きくするような効果も数が増えるにつれ漸減するので、δDが25を超えるような化合物は無い。

Y-MB2014では非線形性が弱いと考え、Y-MB2016では少し下げるように調整した。ところ、逆に一部の化合物で逆にδDが10近辺まで下がる結果になった。これはδDを漸減させる非線形性が悪いとY-MB2019でさらに調整を行った。とろろが結果的には、かえってδDがゼロ近くまで下がるものが現れた。

このように非線形性の調整はとても難しい。

そこで、Y-MB2021では非線形性の導入は行わない、全く新しい推算アルゴリズムを開発した。見かけ上、学習した時の記述性は低そうに見えるが、学習に含まれない予測化合物については、特に中大分子の予測結果はとてもリーズナブルなものであった。

δDfgの予測式

δDfgの推算式では、原点に近い辺りの推算がとても難しい。
Y-MB2016と2019ではδDfgの値が大きい所の記述性が優先されてしまっている。
芳香属化合物、塩素、硫黄化合物などが官能基としての分子間力増大に寄与しているのだろう。

δDfgの小さくなる領域は、フッ素系の官能基が多い。
ここで問題になるのが、フロンのような塩素系とフッ素系を両方持つようなもので、この非線形的なバランスで原点付近の記述性が悪くなる。

非線形性を導入していないY-MB2021は全領域でバランスが取れているが、全体的に誤差は大きめになる。（逆言えば過学習が無く、合わされ込んではいない）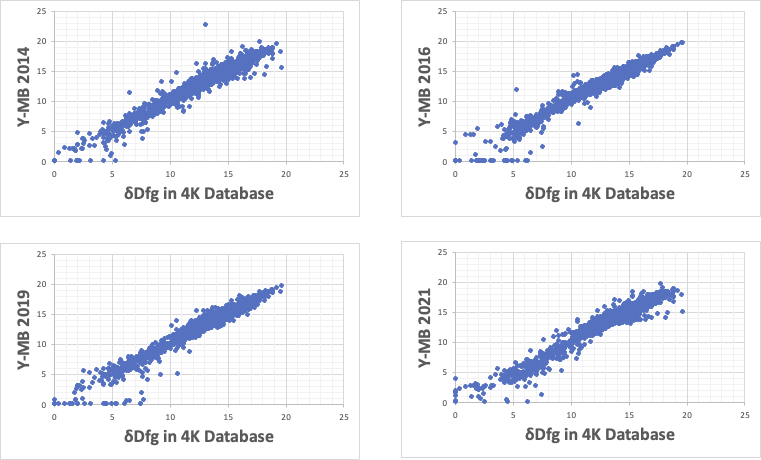


10KDBでの予測性をみると、非線形性を入れた３ちのY-MBは大きく乖離するデータが多いのと、原点付近で、予測値がゼロになる化合物が多い。

Y-MB2021は全領域でバランスが取れていると考えられる。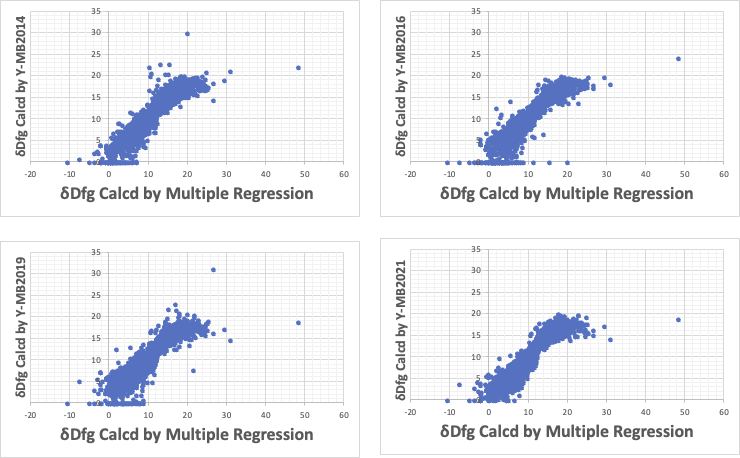

δPの予測式

δPに関しても、最初の３つの非線形式では原点付近の記述性が悪い。

Y-MB2021は全体的に悪い。しかし注意しなくてはならないのは、横軸はあくまで重回帰法の計算値であるということだ。

非線形式を作って、その結果が重回帰式と高い相関があるのでは、そもそも非線形相互作用など無かった事になる。しかし、それは間違である。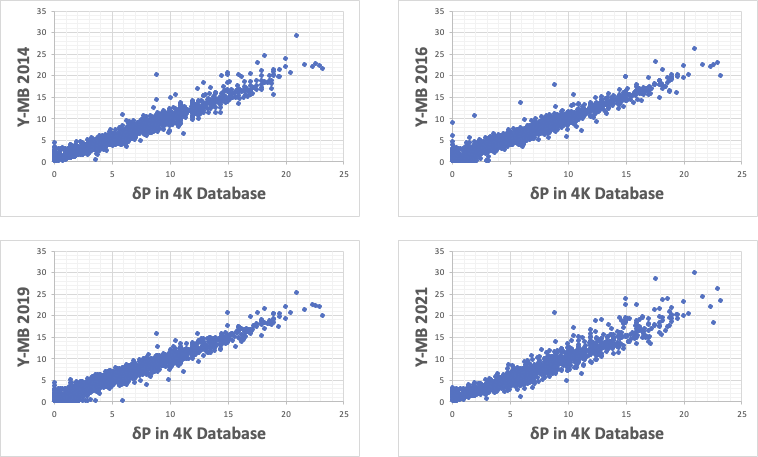

10KDBでの予測値をみると、Y-MB2021だけ傾向が大きく異なる。
δPを大きくする官能基は、カーボネート、アミド、ニトロなどである。

逆にCH2などの炭化水素はどんなに増えてもδPは増えない。

しかし、分子の端についたカーボネート、アミド、ニトロなどはCH2などが増えて分子が大きくなるとダイポールモーメントは大きくなる。

そしてダイポールモーメントが大きくなるとδPを大きくする。

しかし官能基が対称に入るとダイポールモーメントは消えるが、大きなδPは残る。
その時、官能基が増えても重回帰法のようには増えずに、漸減していく。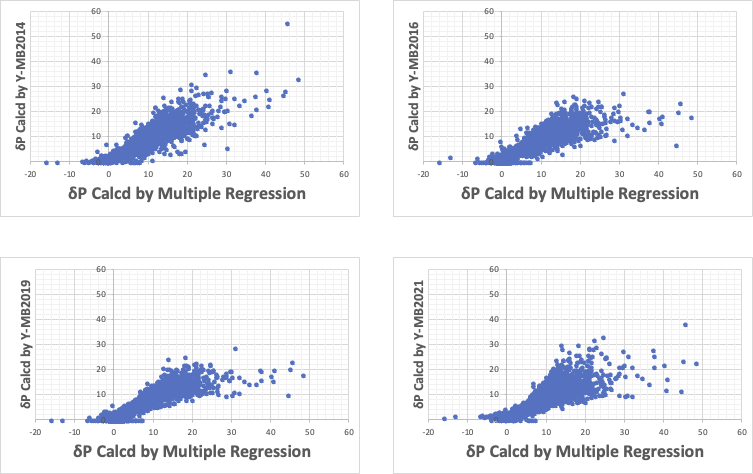

δHの予測式

非線形性の効果が顕著なのは、例えば水素結合項である。

オフィシャルのδHが存在する化合物で一番大きなδHを持つものは水である。過酸化水素水なども大きな値をもつ。

普通の重回帰法を使い原子団の加算値を決めると、例えば水酸基(OH)などは大きな加算値を持つ。そこで、ポリヒドロキシ化合物（例えばグルコース）のδHは計算値上はとても大きな値になる。（実際は分子体積の関数でもあるのでもっと複雑だが。）

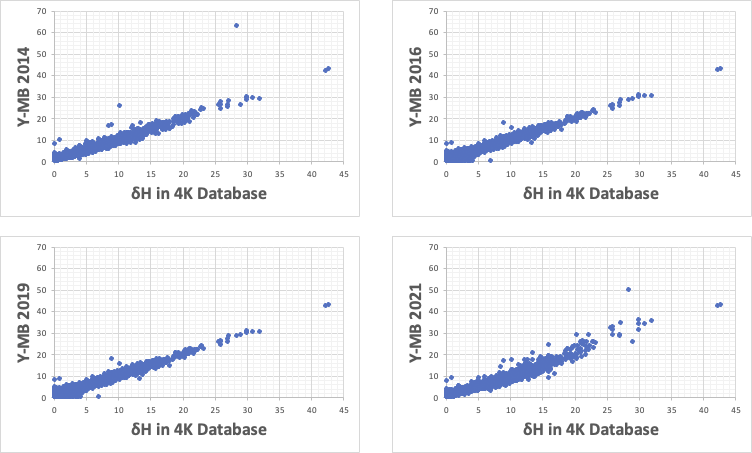
そこで、非線形性を導入すると、水酸基(OH)は分子中の数が増えるにつれて、増加率が小さくなるように調整される。

それは、学習されたデータ（この場合4Kデータ）では上図のように成立する。

Y-MBの計算値は、ほぼ50以下になる。

特徴的なのは、Y-MB2021以外の方法は、原点あたりの精度が非常に低くなることだ。
オフィシャル値は4ぐらいの値があっても計算値は0になったり、逆にオフィシャル値は0であっても計算値は5ぐらいになったりする。

Y-MB2021は原点付近の記述性がとても高くなる。

ところが学習しなかったデータにまで拡張すると、増加率が小さくどころかマイナスになる事がある。下に10Kデータを解析した例を示す。

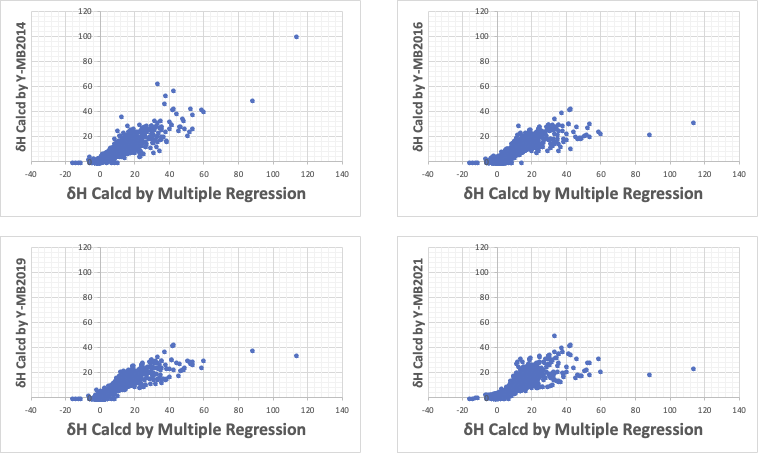
横軸の重回帰法ではポリヒドロキシ化合物はとても大きなδHになってしまう。

Y-MB2014では非線形性がうまく働かず、大きな計算値も出てくる。

そこで、Y-MB2016で調整を行うと40を超えるような値は出なくなったが、今度は上に凸になり、10Kデータセットの中に無い、さらに多くの水酸基を持つ化合物では、計算値がマイナスになるような事があった。

δHではY-MB2019はバランスが取れ始めているが、δDではダメであった。
やはり非線形性を導入する方法ではとても設計が難しい。

検討に随分時間がかかってしまったが、Y-MB2021はこれまでのものと比較してとても高い性能を示している。

δHの分割

δHの分割に関しては別で詳しく説明する。

元々はAbraham教授のAcid, Baseの値を参考にδHを分割しているので、Y-MBではδHacid(HSPiPではδHdo), δHbase(HSPiPではδHac)と表記している。

当初は、Abraham教授のAcid, Baseの値を予測する式を作成して、その比率でδHを分割していた。
そこで次の関係が成立した。

δH² = δHacid² + δHbase²　

しかし現在はδHacidとδHbaseは分子構造から直接推算しているので、上記関係は成立しない。

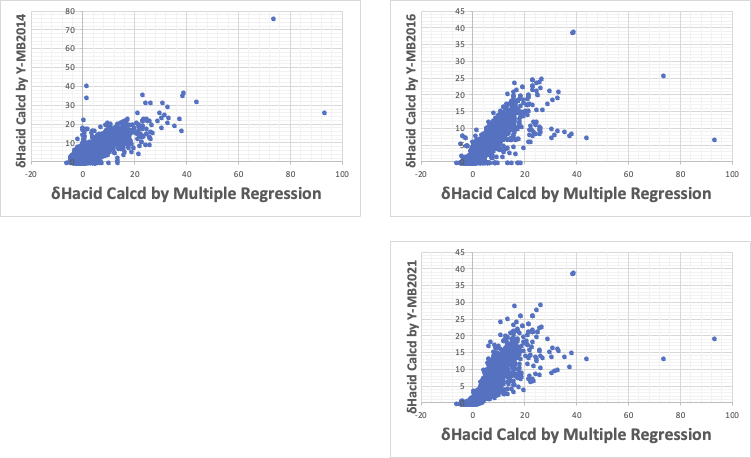
δHacidの予測式

Y-MB2019は作成していない。

δHacidを持つ化合物は、カルボン酸、アルコール、アミン、スルホン酸類ぐらいで、ほとんどの化合物はδHacidを持たない。しかもδHacidを持つ化合物は、皆δHbaseの値も持つ。

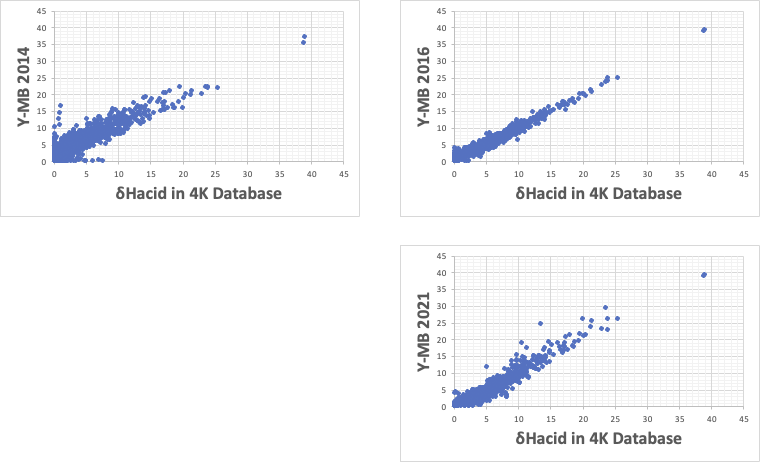
δHbaseの予測式

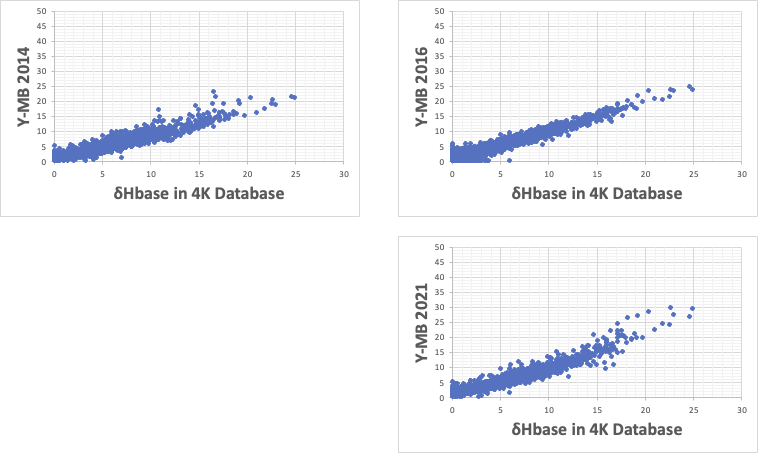
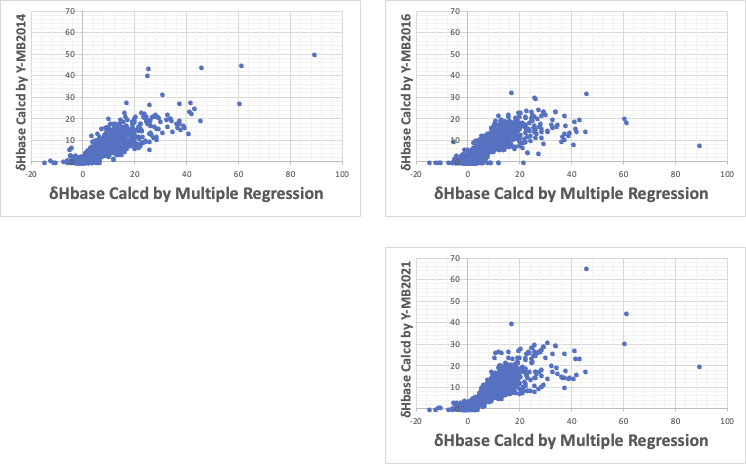
Y-MB2014では不十分。
Y-MB2016では原点付近の記述性が悪い。
Y-MB2021がバランスが取れている。

以上の結果から、

Y-MB2021を新しいHSPiP用のHSP推算式として実装していくこととした。

解析例トップ
　DIYトップページ >
　HSP基礎トップページ >

---

Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください