2024.9.15
物性化学トップページ
Pirikaで提供するプログラム
2011-2024年横浜国大(YNU)で行なった授業で使ったYNU-YMBを公開した。
重原子は15まで、CHNO以外の原子は1以下。パラメータは2013年のものなので古い。JSMEの使い方はこちらを参照して欲しい。
以降、2011.6.15の古い記述。
HTML5制限バージョン(統合化バージョン 2011.6.13)
(Pass Codeがない場合、重原子は8つまで。S, F, Clは使えない)
iPhone/ipod Touchをお使いの方はこちらのプログラムを試して頂きたい。(マウスではタッチイベントが発生しないので分子が描けない)
その他のバージョン
- Joback法ーHTML5バージョン(統合化バージョン 2011.4.16)
- YMBシミュレータ(HTML5 プログラム 2011.6.10 Pass Codeを持っているならこちらの方が精度が高い)
最新の推算方法は、HSPiPに搭載されている。HSPiPに搭載の商用版では、F, Cl, Br, I,S, P, B, Siが使える。芳香族も扱え、最大重原子数は120になる。
プログラムによってどんな原子団が使えるかはこちらで確認のこと
沸点の定義
沸点とは:液体の飽和蒸気圧が外圧に等しくなる温度で、沸騰がおこるときの温度をいう。
すなわち一定圧力のもとでの飽和蒸気とその液相とが平衡に共存している時の温度である。
沸騰点ともいう。
純粋液体では一定外圧における沸点はその液体に固有な物理定数である。外圧を大きくすると沸点は上昇する。通常、圧力1atm のもとでの沸点を標準沸点あるいは単に沸点という。
溶液の沸点は外圧が一定であっても組成の変化に応じて変化する。
沸騰とは:一定圧力のもとで液体がある一定温度に達すると、液体表面からの蒸発のほかに、液体内部からも気化がおこり始める。
この液体内部からおこる気化現象を沸騰 といい、沸騰がおこる温度を沸点という。
沸点では、その液体の蒸気圧は外圧(通常1atm)に等しい。
純粋液体では一定圧力のもとで沸点は一定に保たれ る。
器壁または液中のごみなどが種になり、沸騰がはじまると考えられる。
種の存在をできるだけ少なくすると、過熱が生じることがある。
沸騰の科学についてまとめました。こちらから参照してください。
推算法
蒸気圧の推算にはいくつかの方法が知られている。
- Meissner
- Lydersen, Forman, Thodos, JOBACK
- Miller
- Ogata and Tsuchida
- Somayajulu and Palit
- Kinney
- Stiel and Thodos
一番基礎になる方法はJobackの原子団寄与法(Wiki Pedia)によるものだろう。この方法は各原子団に、原子団が一つ増えるごとに、沸点がどれだけ増えるのかという加算値を求め、その足し合わせで沸点を予測するものだ。
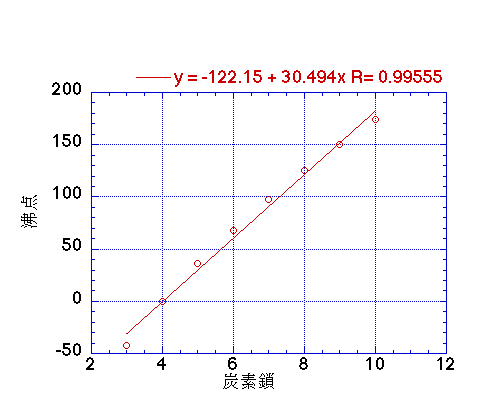
例えば、プロパンからデカンまでの沸点を炭素数に対してプロットすると上の図のようになり、炭素が一つ(CH2がひとつ)増えると30.49℃沸点が上昇することがわかる。
同じ組成式、例えばC6H14でも分子の形状、すなわち、枝別れの状態によって沸点は変わってくる。
ヘキサン(68℃)、3-メチルペンタン(63℃)、イソヘキサン(60℃)、2,3-ジメチルブタン(58℃)、ネオヘキサン(49℃)
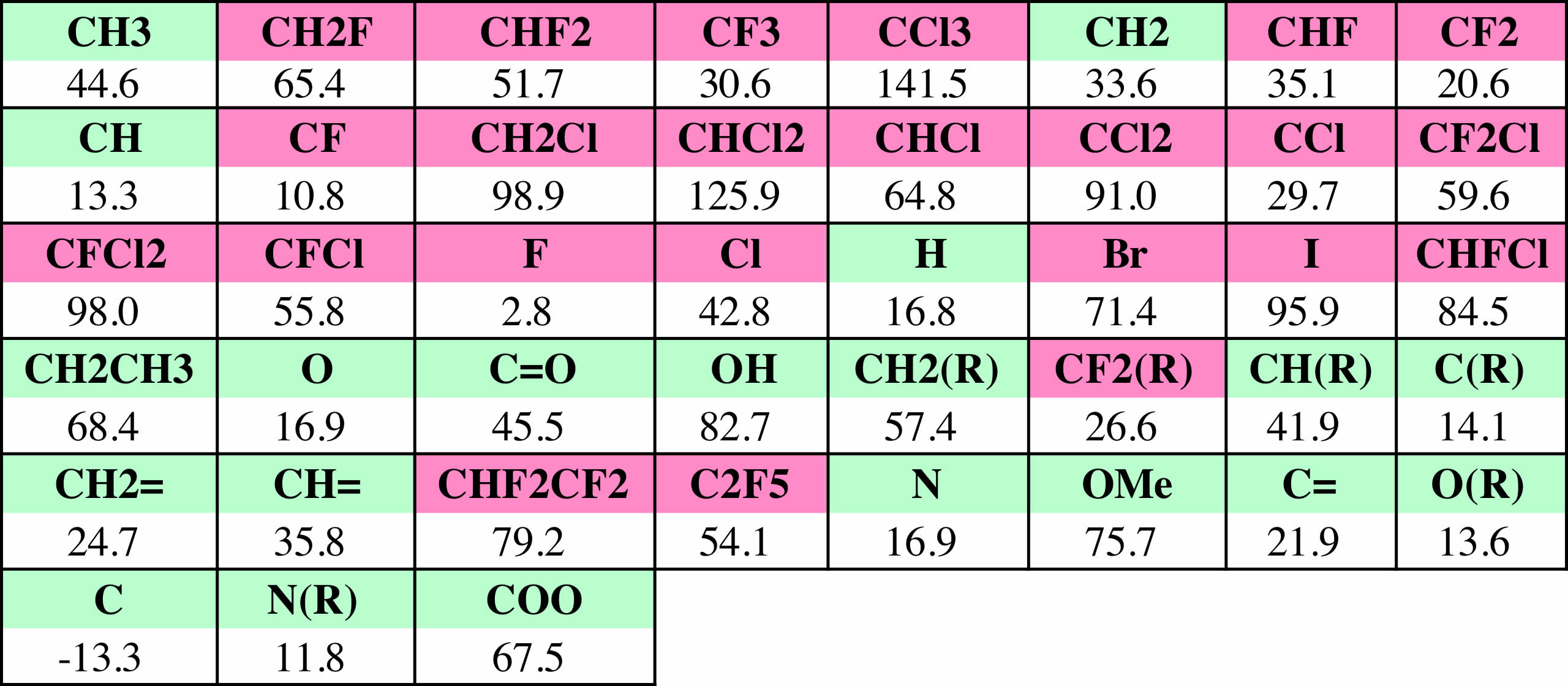
そこで、CHやCという原子団を定義して加算値を求めていく。
こうした事を40個程度の原子団に対して統計的に定めたのがJoback法だ。
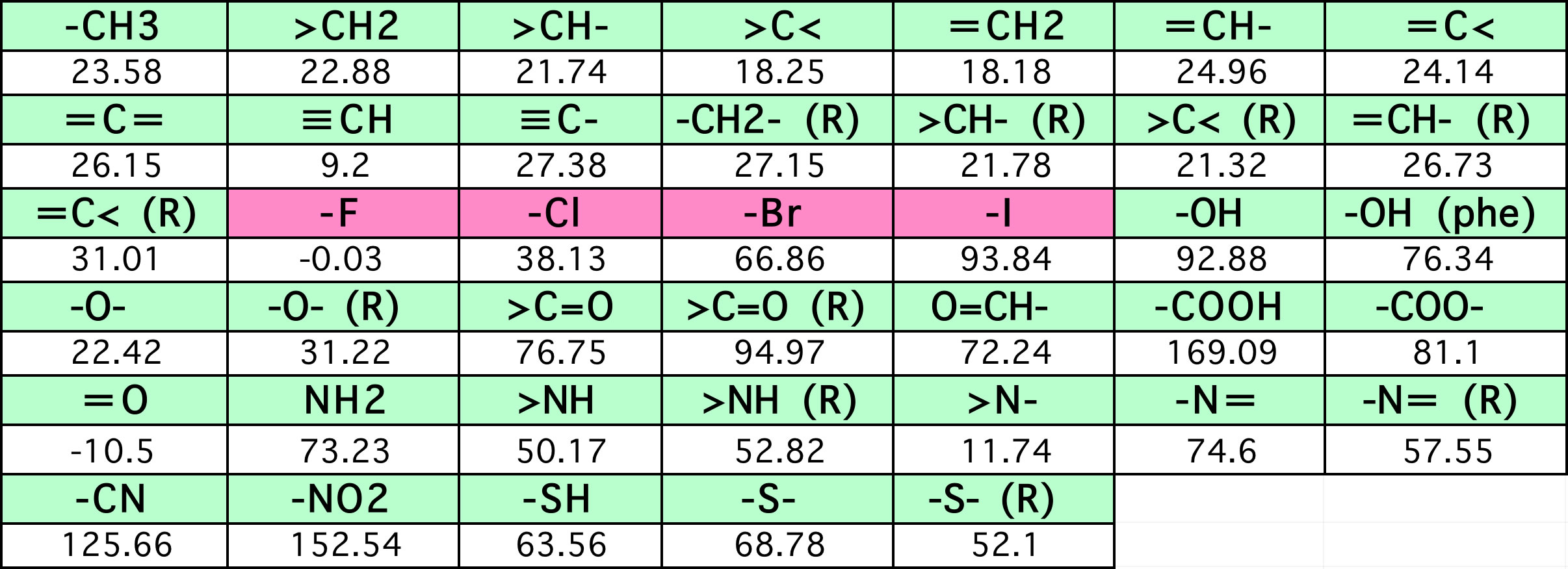
(R)がついている原子団は環状化合物に適用する。(phe)はフェノールのOHである。
JobackとReidは1987年に脂肪族と芳香族炭化水素の沸点の概算値をグループ寄与法を用いて計算する方法を提案した。沸点は分子を構成する部分構造の寄与の総和で推算される。
Tb=198.2+sigma(ni * deltabi)
Tb: 標準沸点,[K]
ni: i番目の部分構造の数
deltabi: JOBACKのi番目の部分構造の沸点に対する寄与度, [K]
この計算式は沸点が500Kを超える場合には過大評価をする傾向がある。
次の2つの多項式がこの問題を修正する。
Tb(corr)=Tb – 94.84 + 0.5577 Tb – 0.0007705 Tb2, (Tb < 700K) Tb(corr)=Tb+282.7 – 0.5209 Tb, (Tb > 700K)
しかるべき多項式を使った場合には,このモデルは絶対誤差15.5K,そして平均的な%誤差は3.2%を与える。
Joback法による沸点推算についてさらに詳しく知りたい方は、
McGRAW-Hill International Editions 1987
The Properties of GASES & LIQUIDS 4th Edition
Robert C.Reid, John M. Prausnitz, Bruce E. oling
を参照のこと
非常に簡便ではあるが、この方法の欠点は定義されていない原子団があると計算できなくなる点だ。
例えばアミド(C(=O)NH2)はケトン(>C=O)とアミン(NH2)の足しあわせにはならない。
さらに、分子を原子団に分割する際に原子団同士の結合情報が失われるという欠点を持つ。
そこでアミノ酸(RC(NH2)COOH)のようにアミンとカルボン酸が一つの炭素についている場合には、我々はこれが固体になり、多くの場合、沸点は持たず、加熱すると分解してしまうことを知っている。
しかし、原子団に分割してしまうとアミンとカルボン酸の加算因子分だけ上昇した沸点を答えとして返してしまう。
また、こうした線形式は同じ複数の官能基が導入されるごとに上昇率がだんだん下がるといった非線形性には追随できない。上のプロパンからデカンの沸点の図でも、だんだん上昇率は下がっているのがわかるだろう。
こうした、官能基間相互作用と非線形性を同時に満たす解析方法として、ニューラルネットワーク法(NN法)が使われる例も多いが、NN法は記述性は高いが、予測性が低く、また結果をJoback法のように簡単に検証することもできないので、利用度は下がっているように思える。
Pirikaの古いJAVAの物性推算法はNN法を使っている。ニューラルネットワークがどのように学習を進めていくかは、こちらのデモをご覧頂きたい。
それでは、線形回帰を使うか、非線形回帰を使うかは別として、どうやったらこのJoback法を改良できるかを考えてみよう。
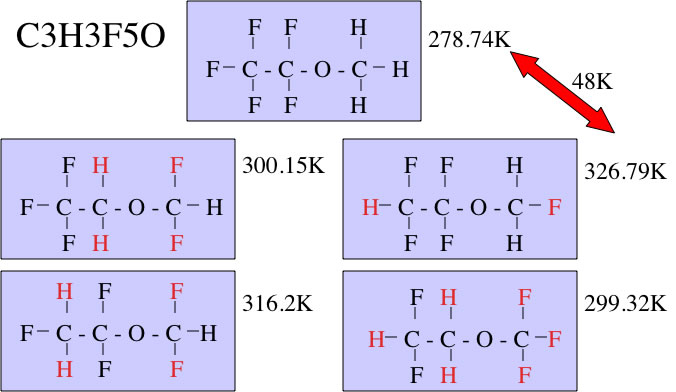
例えばこのJoback法のテーブルにはハロゲン原子は単体の4つしかない。そこで、例えばC3H3F5Oという構造をデータベースから沸点を探索してみると、沸点は48℃異なるものがあることがわかる。
Jobackのテーブルで、CH3, CH2, CH, Cの加算因子が5℃程度の違いしか与えないことから、Joback法でフロン代替の化合物を物性推算して設計することは不可能であることがわかるだろう。
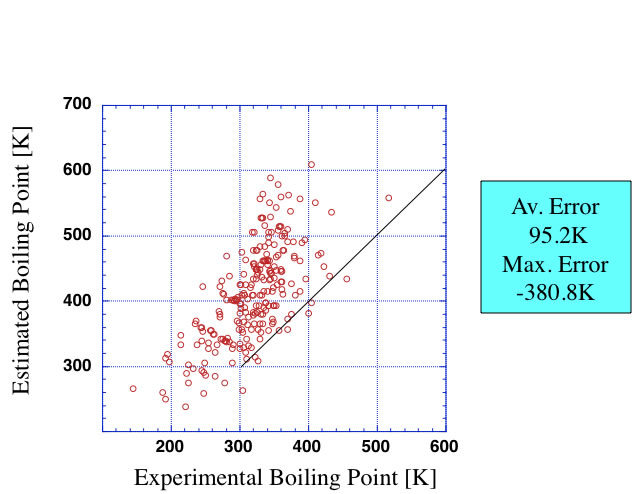
データベースからハロゲン原子を含む化合物だけを取り出して、Joback法で沸点を推算すると下のグラフのようになり、平均で95.2Kずれてしまうことがわかる。
そこで、ハロゲン原子の原子団を追加することによって推算精度の向上を図ることにする。
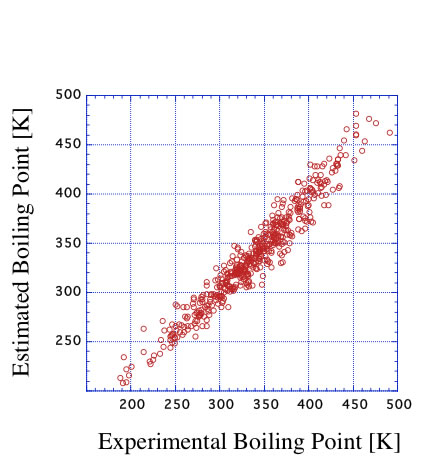
すると、推算精度は非常に向上する事がわかる。平均誤差は10.5K程度になる。
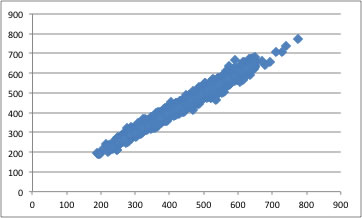
ニューラルネットワーク法を使うとさらに平均誤差は小さくなるが、ニューラルネットワークの質が悪いと予測性能は逆に非常に悪くなることがある。
それを避けるには、とにかくデータを増やすしかない。ハロゲン化合物、芳香族化合物とデータを増やすと、それにあわせ官能基の数も増え、官能基の数が増えた分、また学習させるデータを増やすというイタチごっこが延々と続くことになる。
Pirikaの最新の方法は、1万を超えるデータセットから推算式を構築したもので、官能基は167種類定義されている。その一覧はこちらを参照していただきたい。
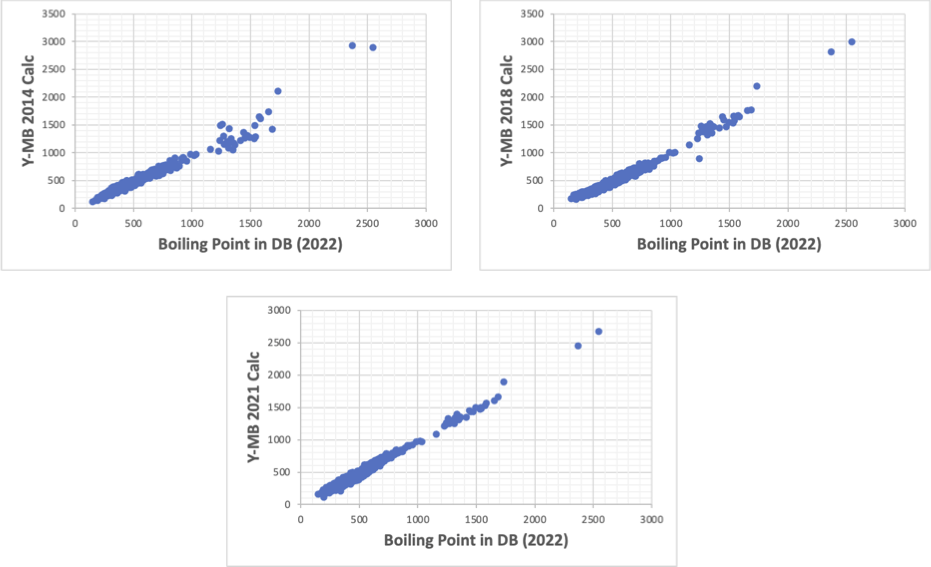
4855化合物の沸点から、このぐらいの精度で沸点を推算する式が搭載されている。
この機能はHSPiP(Hansen Solubility Parameters in Practice)というプログラムに搭載されている。
さらにこれを改良するにはどうしたら良いだろうか?
原子団寄与法の問題点のうち、非線形性についてはNN法を使えば改良できる。しかし、原子団の結合情報がなくなってしまうことに対してはNN法を使っても改良できない。
QSPR法を使い、記述子として原子団ではなく、分子軌道計算の後に、分子体積、プラス/マイナスにチャージされている表面積、ダイポールモーメントなどを入力するニューラルネットワークも開発されている。
電荷平衡法による電荷の計算も非常に有効だ。
2次元QEQ法でも説明したが、C2H5という原子団の加算因子を炭化水素化合物のみからつくるとC2H5は非常に非極性な基になり、沸点の加算値も小さくなる。
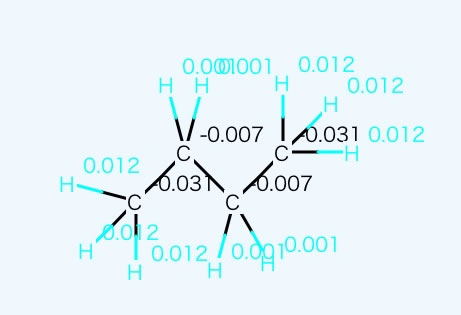
同様にC4F10も分子表面はフッ素に覆われていて、電荷もほぼ一様なので、C2F5も非極性な基で加算値もさらに小さくなる。
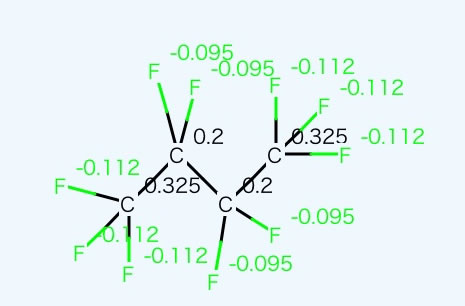
この2つが組み合わさった場合、両方共加算値が小さいので、沸点の推算値が小さめな値になってしまうが、電荷平衡法で計算すると、大きく分極していることがわかる。
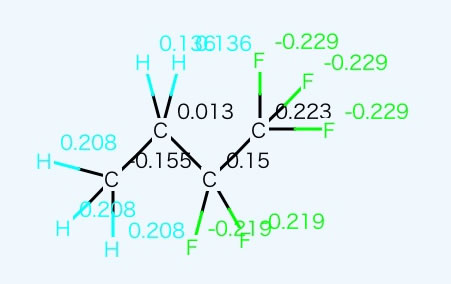
これを補正項として取り込むことが可能であれば、沸点の推算も格段に精度があがると考えられる。
2次元QEQは非常に簡単に電荷を計算できるので、将来が楽しみな技術である。
そうしたものが実用化するまでは、現実的には実験値の沸点を使うことを推奨している。化学工学で取り扱う化合物の沸点が不明なことは稀であろう。
最悪、沸点が既知の化合物とガスクロを打てば、大体の沸点は見積もれる。
C6H14のヘキサン(68℃)、3-メチルペンタン(63℃)、イソヘキサン(60℃)、2,3-ジメチルブタン(58℃)、ネオヘキサン(49℃)分子の形状効果をさらに検討してみる。
こうした化合物の分子表面積を計算し沸点に対してプロットすると下に示す図になる。一応表面積が大きくなると沸点が高くなる傾向がみられるが相関係数は0.82898とあまり高くない。
沸点では分子の運動エネルギーが分子間力に打ち勝つことが必要なので、接触面積の大きい分子はそれだけ高い温度(運動エネルギー)が必要だと考えられている。
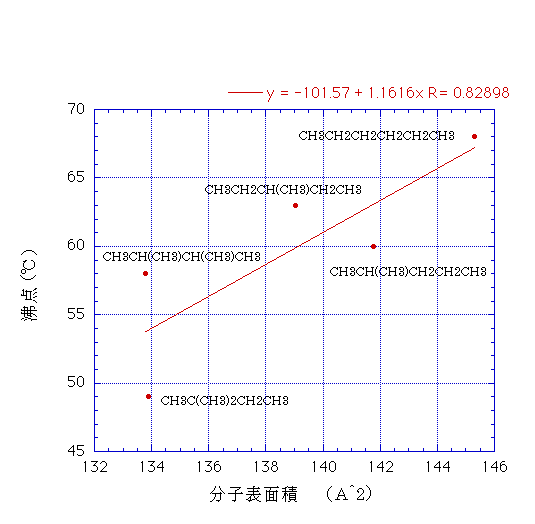
しかし、ほとんど同じ分子表面積である2,3-ジメチルブタンとネオヘキサンで沸点が9℃も異なることから、こうした表面積以外の(例えば分極の)効果などで沸点の値が変わると考えられている。
一般的には次のような事が知られている。
- molecular size become larger, boiling point become larger.
- compare with spherical structure and stick type structure, spherical structure become lower boiling point. ( because of accessible surface area? )
- hydrogen bond make boiling point raise dramatically
- Dipole moment make boiling point (maybe) raise
- Halogen atom make boiling point bring down
沸点と分子のトポロジーについては、
朝倉書店 朝倉化学講座5 構造と物性
細矢 治夫 丸山 有成 著
に詳しく書かれているのでそちらを参考にしてください。
文献(99-2-4の時点)うーーーん最近勉強不足だな。。。
Prediction of Boiling points and Critical Temperatures of Industrially Important Organic Compounds from Molecular Structure
J. Chem. Inf. Comput. Sci. 1994, 34, P947-956
Leanne M. Egolf, Matthew D. Wessel, and Peter C. Jurs
Design Institute for Physical Property Data(DIPPR)のデータベースを解析。多重線形回帰分析とニューラルネットワークを用いて298有機化合物の沸点、臨界温度を検討。
ADAPTというプログラムを使い、各分子のデスクリプタ(記述子)を発生させ計算を行っている。
Normal Boiling Points for Organic Compounds: Correlation and Prediction by a Quantitative Structure-Property Relationship
J. Chem. Inf. Comput. Sci. 1998, 38, P28-41
Alan R. Katritzky, Victor S. Lobanov, and Mati Karelson
C,H,N,O,S,F,Cl,Br,I を含む612分子の沸点を検討。AMPAC AM1 で分子軌道計算を行いその結果をCODESSAというプログラムの入力に使い、各分子のデスクリプタを発生させ計算を行っている。
Neural Network – Topological Indices Approach to the Prediction of Properties of Alkene
J. Chem. Inf. Comput. Sci. 1997, 37, P1146-1151
Shuhui Liu, Ruisheng Zhang, Mancang Liu, and Zhide Hu
トポロジカル指標をニューラルネットワークの入力値に用いてアルケン化合物の沸点、密度、屈折率を推算。シス、トランス効果を加味。
Group Contribution-Additivity and Quantum Mechanical Models for Predicting the Molar Refractions, Indices of Refraction, and Boiling Point of Fluorochemicals
J. Phys. Chem. 1995,99,P13909-13916
Thao D.Le and Jeffry G. Weers
PM3の計算により得られたPolarizabilityの値を用いて含フッ素化合物の屈折率、沸点を推算。
Spectral Moments od the Edge-Adjacency Matrix of Molecular Graphs. 2. Molecules Containing Heteroatoms and QSAR Applications
J. Chem. Inf. Comput. Sci. 1997, 37, P320-328
Ernesto Estrada
グラフ理論を用いて、58個のアルキルアライド化合物の沸点を推算。
Spectral Moments od the Edge-Adjacency Matrix of Molecular Graphs. 3. Molecules Containing Cycles
J. Chem. Inf. Comput. Sci. 1998, 38, P23-27
Ernesto Estrada
80個の環状化合物の沸点を推算。
The Detour Matrix in Chemistry
J. Chem. Inf. Comput. Sci. 1997, 37, P631-638
Nenad Trinajstic, Sonja Nikolic, and Bono Lucic
Detourマトリックス法とWienerらの方法を76のアルカン、シクロアルカン化合物で比較。
Approach to Estimation and Prediction for Normal Boiling Point(NBP) of Alkanes Based on Novel Molecular Distance-Edge (MDE) Vector, λ
J. Chem. Inf. Comput. Sci. 1998, 38, P387-394
Shushen Liu, Chenzhong Cao, and Zhiliang Li
分子中の端(Edge)の距離を用いて分子の沸点を推算。
Design of Topological Indices. Part 10. Parameters Based on Electronegativity and Covalent Radius for the Computation of Molecular Graph Descriptors for Heteroatom-Containing Molecules
J. Chem. Inf. Comput. Sci. 1998, 38, P395-401
Ovidiu Ivanciuc,Teodora Ivanciuc, and Alexandru T. Balaban
酸素や硫黄などの原子を含む185化合物についてグラフ理論を応用して沸点を推算。
Extension of Edge Connectivity Index. Relationships to Line Graph Indices and QSAR Applications
J. Chem. Inf. Comput. Sci. 1998, 38, P428-431
Ernesto Estrada, Nicolais Guevara, and Ivan Gutman
分子中の端(Edge)の結合指標を用いて沸点をはじめとする8つの物性を推算。
Polarity-Numbers of Cycle-Containing Structures
J. Chem. Inf. Comput. Sci. 1998, 38, P715-719
Istvan Lukovits and Wolfgang Linert
Wienerらによって提案されたポーラリティー数を改良し、炭化水素化合物の沸点を推算。
Correlation of Boiling Points with Molecular Structure for Chlorofluoroethanes
J. Chem. Inf. Comput. Sci. 1998, 38, P715-719
Terry S. Carlton
52のChlorofluoroethane化合物に対し6つの指標を用いて沸点を推算。
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
