2024.9.27
物性化学トップページ
表面張力の理解のために(2013.8.16)も参照してください。
沸騰の科学についてまとめました。こちらから参照してください。表面張力の温度依存性について参考になると思います。
次世代HSP技術、HSPと表面張力を参照してください。
Pirikaで提供するプログラム
2011-2024年横浜国大(YNU)で行なった授業で使ったYNU-YMBを公開した。
重原子は15まで、CHNO以外の原子は1以下。パラメータは2013年のものなので古い。JSMEの使い方はこちらを参照して欲しい。
以降、2011.6.26の古い記述。
YMBシミュレータ(HTML5 プログラム 2011.6.10 Pass Codeを持っていれば、精度高く、表面張力の温度依存性も含め計算できます。)
シス、トランス化合物はその平均値を返します。
芳香族用のパラメター、ハロゲン化合物のパラメーターは入っていません。
(分子の描き方はこちらを参照してください。)
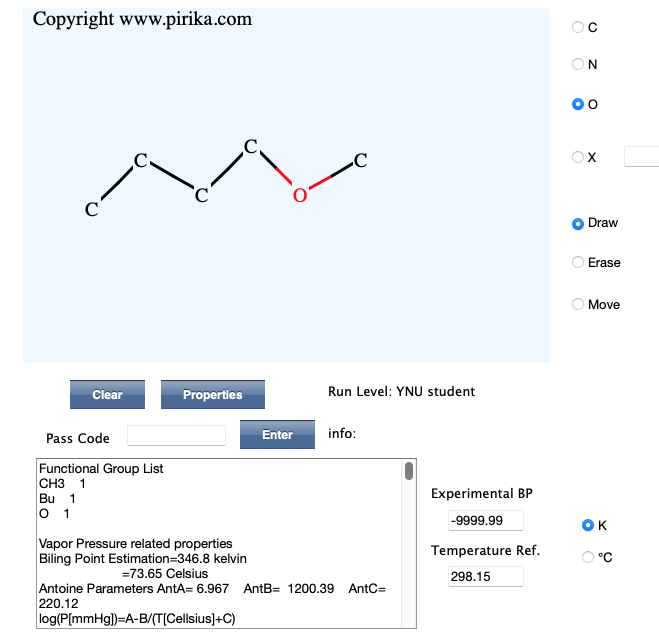
最新の推算方法は、HSPiPに搭載されている。HSPiPに搭載の商用版では、F, Cl, Br, I,S, P, B, Siが使える。芳香族も扱え、最大重原子数は120になる。(計算結果は表には出ないがクリップボードには載っている)
プログラムによってどんな原子団が使えるかはこちらで確認のこと
原理
液体表面の分子は非対称な力を受けやすい。
一般的に、我々は液体の表面と(空気や液体の蒸発した)気体のあいだの界面だけを考慮に入れる。
もし、気体や蒸気の密度が小さいなら、液体表面の分子は液体に向かって引き寄せられる。
気体や蒸気が引き寄せる力はかなり小さい。
その結果、表面には表面積を減らして、物質の塊と容器の壁と一致させようとする張力が発生する。
この力はある温度ごと、液体ごとに特徴的なものである。
この表面張力は単位長さあたりの力として定義され(一般的にはdynes/cm)、Sで表される。
これは面積あたりのエネルギー (ergs/cm2)で表されることもある。
ほとんどの有機化合物の液体は室温で、 25から40 dynes/cmの表面張力を持つが、多価アルコール化合物では65 dynes/cmになるものもある。
それに対して、水の表面張力は25°Cで72 dynes/cmにもなる。
最も一般的な表面張力Sの推算方法はMacleod-Sugden法である。
これを用いて計算するためには、パラコールと密度(もしくは、モル体積)が必要になる。
この場合表面張力の温度の依存性は密度だけから考慮される。
しかし、密度の温度依存と表面張力の温度依存は広い範囲で一致しているとは言えない。
Pirikaの方法(YMBシミュレータ)はニューラルネットワークに温度の効果も取り込んで構築されている。
推算法
Macleod-Sugden法
表面張力の推算法としては、Macleod-Sugdenが最も著名である。MacLeodは表面張力と液体密度の関係を経験的に導き出した。後にSugdenはMacLeodの式に現れる経験的な定数が、パラコールと呼ばれる構成要素の定数と同じことを示した。Sugdenの導き出した式は、
s1/4 = P (rL – r v) / M
ここで
s = 表面張力 (dynes/cm)
P = parachor(パラコール)
rL =液体密度 (g/cm^3 )
r v = 気体密度 (g/cm^3 )
M = 分子量 (g/mol)
パラコールは2つの液体のあいだの相対的な体積として視覚化でき、温度には独立であった。Quayleは広範囲の有機化合物に適用可能なパラコールを推算する包括的なレビューを提案した。ほとんどの場合、 r vは rLより十分に小さいので、無視することができる。
s = (P*rL / M )4
この式が表面張力を推算する基本的な式である。典型的な誤差は平均5%以内であるが、ものによっては30%の誤差もありうる。
このパラコールは分子屈折[RD]と相関があることが知られている。(2013.8.16)
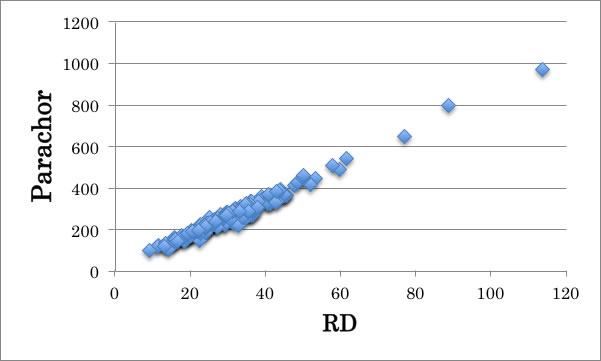
詳しくはこちらのページを参照のこと。
YMBシミュレータは液体密度をニューラルネットワーク法で推算する。
例えばCH3COOC2H5の場合、
P=214.8
M=88.107
Density=0.90063
s = (P*rL / M )^4 = (214.8*=0.90063 / 88.107 )^4 =23.24 dyne/cm
となる。実験値は23.97 dyne/cm at 20°Cであるので悪い推算ではない。
しかし、この方法は密度に対して非常に鋭敏になってしまう。
Density ばらつき -3% (0.90063 -> 0.874 ) s =20.58 dyne/cm (-14%)
Density ばらつき +3% (0.90063 -> 0.928 ) s =26.16 dyne/cm (+9%)
密度が3%変化しただけで、10%近く誤差が生じてしまう。
Macleod-Sugden法による表面張力推算についてさらに詳しく知りたい方は、
McGRAW-Hill International Editions 1987
The Properties of GASES & LIQUIDS 4th Edition
Robert C.Reid John M. Prausnitz Bruce E. oling
を参考にしてほしい。
Van Krevelenはポリマーの表面張力の推算式を構築しているが、これも密度に対して非常に鋭敏である。
Van Krevelenの表面張力推算についてさらに詳しく知りたい方は、
“Properties of Polymers” D.W. Van Krevelen
ELSEVIER SCIENCE B.V.
を参照してほしい。
原子団のパラコール
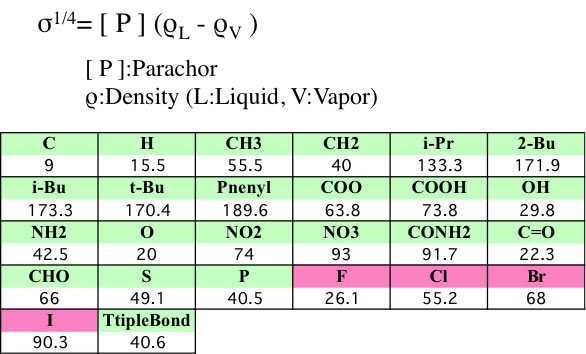
この式を使って””Chemical properties handbook, Yaws””にあるデータを検証すると以下のようになる。
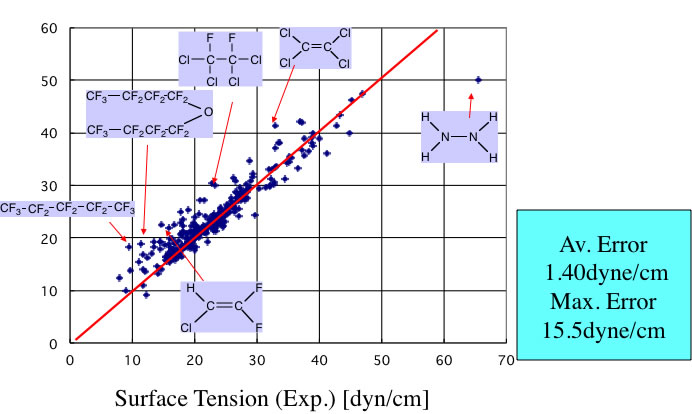
ハロゲンを含有する化合物で大きくずれる。これは、一つにはハロゲン系の化合物は密度が大きく、蒸気の密度を無視できないからというのも一つの理由であろう。
しかし、ハロゲンの原子団の定義が少ないことも一つの理由であろう。そこで原子団の拡張を行ってみる。
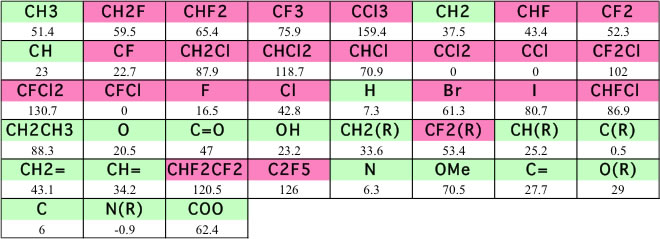
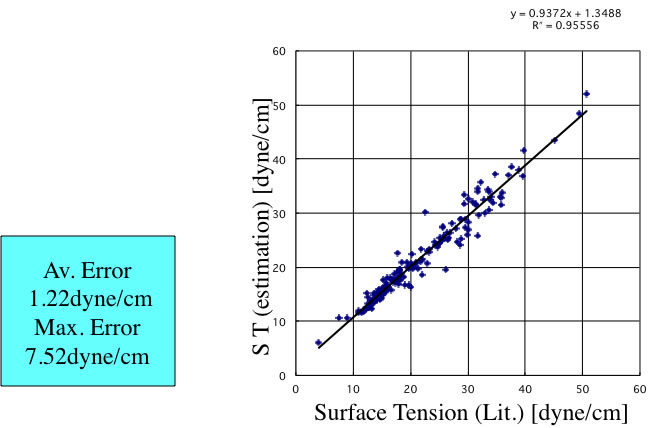
こうした原子団の拡張は有効で、精度はそれなりに向上する。さらにニューラルネットワークを用いた推算式が、YMBシミュレータに搭載されている。この精度は次のようになる。
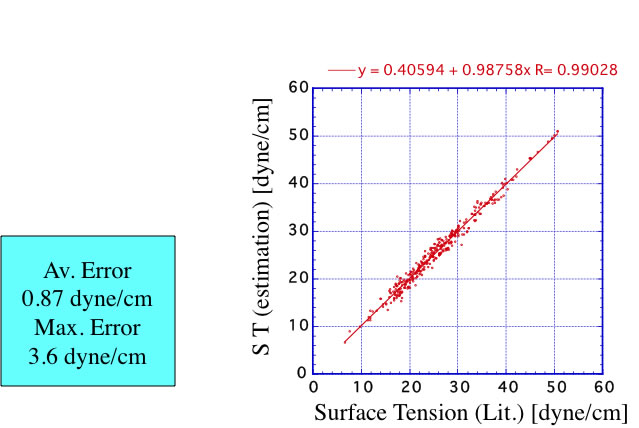
このように、室温における表面張力は原子団寄与法をベースにしたこれらの方法で推算することができる。問題となるのが、温度依存性をどうやって推算するかだ。表面張力の温度依存性を密度の変化だけで記述しようとすると、非常に大きな誤差になってしまう。
Brock-Bird法
この温度依存性をうまく取り込んでいるのが、対応状態原理の一種のBrock-Bird法だ。これは次式で表面張力を計算する。

この式を使って””Chemical properties handbook, Yaws””にあるデータを検証すると以下のようになる。
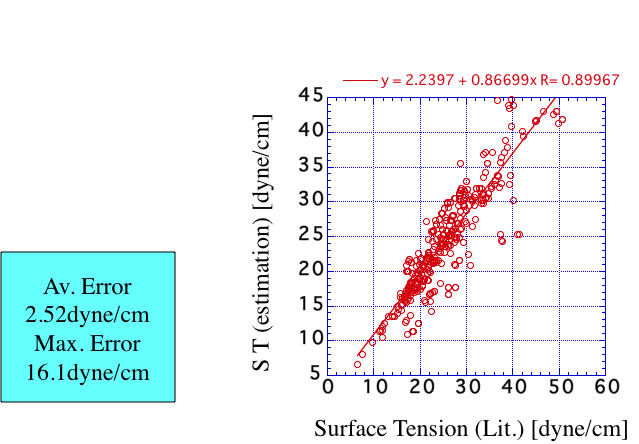
測定温度が室温以外の場合にはこちらを使うのが妥当だろう。
YMBシミュレータに搭載したのは、QSPR式で次のような精度になる。
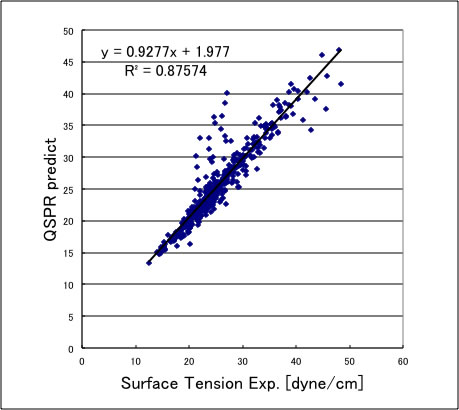
上方にずれる化合物は、カルボン酸化合物なので、これらには使うことができない。この推算式をアセトンに使うと以下のような結果になる。絶対値のずれは大きいが温度の依存性は良好に再現できている。
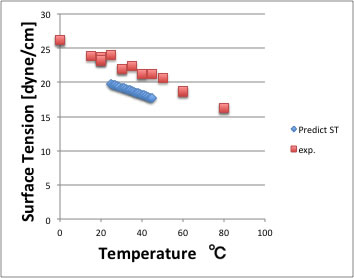
面張力の実験値は、データ集によっても比較的値がばらつく物性なので、構造のみからこの程度推算出来れば十分であろう。
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
