2024.9.16
物性化学トップページ
Pirikaで提供するプログラム
2011-2024年横浜国大(YNU)で行なった授業で使ったYNU-YMBを公開した。
重原子は15まで、CHNO以外の原子は1以下。パラメータは2013年のものなので古い。JSMEの使い方はこちらを参照して欲しい。
以降、2011.6.15の古い記述。
HTML5制限バージョン(統合化バージョン 2011.6.13)
(Pass Codeがない場合、重原子は8つまで。S, F, Clは使えない)
iPhone/ipod Touchをお使いの方はこちらのプログラムを試して頂きたい。(マウスではタッチイベントが発生しないので分子が描けない)
その他のバージョン
- Joback法ーHTML5バージョン(統合化バージョン 2011.4.16)
- YMBシミュレータ(HTML5 プログラム 2011.6.10 Pass Codeを持っているならこちらの方が精度が高い)
最新の推算方法は、HSPiPに搭載されている。HSPiPに搭載の商用版では、F, Cl, Br, I,S, P, B, Siが使える。芳香族も扱え、最大重原子数は120になる。
プログラムによってどんな原子団が使えるかはこちらで確認のこと
沸騰の科学についてまとめました。こちらから参照してください。臨界温度の理解に奴に立つと思います。
臨界温度の推算
臨界温度( Tc ), 臨界圧力 ( Pc ), 臨界体積 ( Vc ) は純物質の物性定数の中で非常に広範に用いられる物性値である。これらの臨界定数は化学工学の分野でも非常に重要だ。なぜなら多くの熱物性値は沸点と臨界定数から対応状態原理を使って推算できるからだ。そこで精度の高い臨界定数の推算は非常に重要になる。
臨界定数を推算する式はいくつか知られている。
Ambrose
Lydersen
JOBACK
Fedors
Riedel
Vetere
Klincewicz
これら全ての式で,臨界温度を推算するには標準沸点の値が必要になる。
そして,Tcの推算精度は入力した沸点の値に強く依存してしまう。
従って全く未知の化合物の場合,沸点を推算して,推算した沸点を使って臨界温度を推算することになり,誤差が2重になってしまう。
それに対してPirikaの推算式はニューラルネットワークを使って沸点を使わずに構造から直接臨界温度を推算してしまう。
臨界温度の推算では原子団寄与率のトータルと,分子量(重原子の数)などから良好に相関がとれる。
しかし,臨界温度,臨界圧力どちらの場合も,原子団ー原子団相互作用があるような分子の場合には正しい推算値を与えることができない。
そこで原子団(官能基)を2種類以上持つ化合物の推算誤差は5%近くになる。
Pirikaの推算式は原子団ー原子団相互作用だけでなく,水素結合の効果も取り込むので,従来の方法と比べても推算精度は高い。
臨界体積や臨界密度(分子量/臨界体積)の実験値はTcやPcほどは無い。
いくつかのデータ集では実験値ではなく推算値の値を収録している。
この物性値は構造にそんなに敏感ではない。しかし,この値を用いて液体密度の推算を行おうとした場合には,実験値なのか推算値なのかは大事だ。
Pirikaのニューラルネットワーク法は,分子軌道計算で最適化した分子構造の分子体積から補正係数を導き出すやり方を使っている。
推算式
臨界温度の推算はLydersenを始め様々な式が知られている。基本的な計算方法はあまり違わず、各原子団に加算因子を割り振り、沸点とで臨界温度を推算する。その中でもJobackのものが一般的(Wiki Pedia)だろう。次式で臨界温度を推算する。
Tc = Tb[0.584 + 0.965ΣΔTc – (ΣΔTc)^2 ]^-1
加算因子(Tcは一番左のもの)
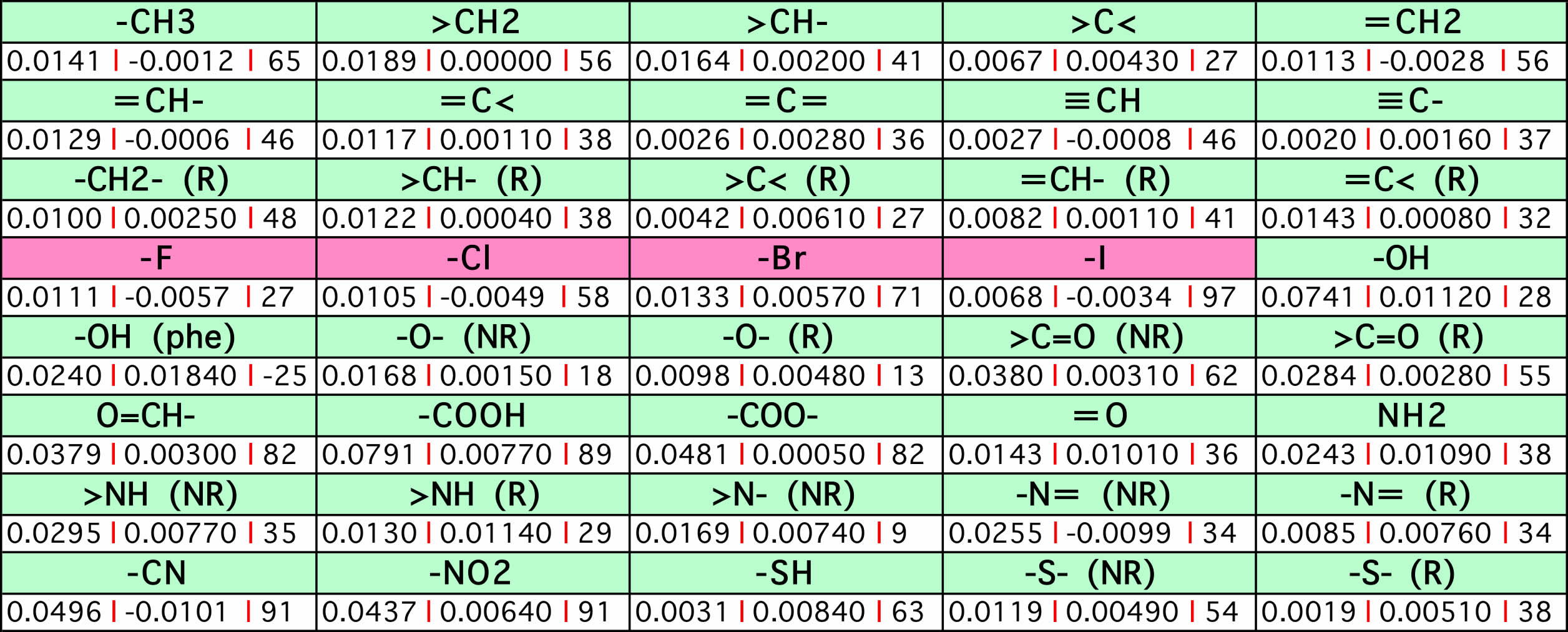
この推算精度は上に示すように、平均誤差7.2Kと非常に高い。ところが実際にこの方法が高い推算精度を与えるのは沸点が実験値を用いているからだ。
もし、沸点を推算値、例えばJoback法の沸点の推算値を用いた場合には、沸点の推算値に改良法でも平均10K程度の誤差を含む。
おおよそ、その1.5倍程度の誤差につながるので、臨界温度は平均でも15Kの誤差を持つことになる。
従って原子団を拡張して、その原子団の加算値を定義しても、予測値はそれほど良くはならない。
また、そうしたことをやろうとすると別の問題が持ち上がる。データベースとして非常に定評のあるDipper801を調べてみると、1319化合物のうち、臨界温度が実験値のものは420化合物しか無い。
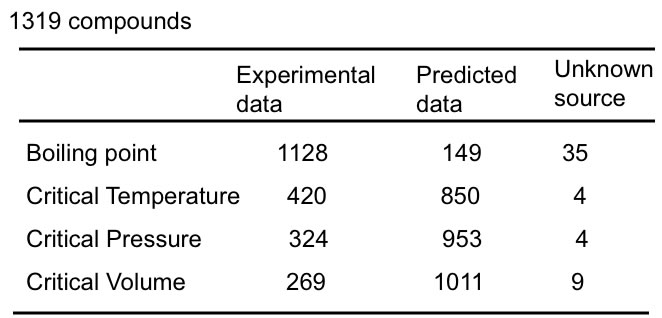
このデータから新しく決めた原子団の加算値を決めなくてはならないので、非常に誤差が大きくなってしまう。
ましてやニューラルネットワーク法のように学習データを大量に使わないと精度のでない方法を使う場合には致命的になる。
そして、この実験値が今後増えるかといえば、化合物が大きくなれば臨界温度も高くなり、測定上の問題点も増え、化合物の熱安定性も問題になり、これ以上大幅に増えることは期待できない。
それでは、どうしたらいいだろうか?
例えば、臨界温度はおよそ沸点の1.5倍だという経験則がある。そこで臨界温度が未知なら沸点*1.5で代用すればいいという考え方だ。実際にGases&Liquidsのデータベースの値で見てみよう。
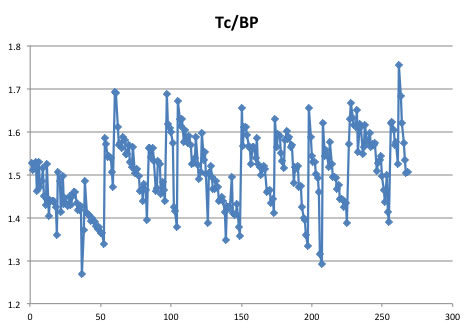
確かに平均値としてはTc/BPは1.5になると言っていいだろう。
ただし、学生にそう教えていいのは、亀の子の解っていない数学者や統計学者だけだ。
化学の先生がそう教えているのなら問題だ。何故あるものは1.7であるものは1.3なのだろうか? それを教えなければ化学の先生とは言えない。
このデータの中から、芳香族、炭化水素、オレフィンの化合物だけを抜き出して、分子の体積(HSPiPで計算した)に対してプロットしてみると、下のようなグラフになる。
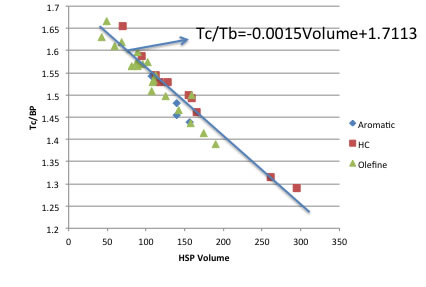
この図から明らかなように、分子体積の小さな化合物はTc/BPが1.7に近くなり、分子が大きくなるとTc/BPが小さくなる事がわかる。その体積の補正項を導入すると推算式はどのくらい改良されるだろうか?
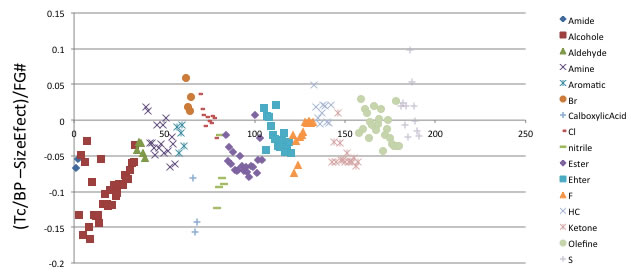
化合物の種類ごとにプロットすると上の図のようになる。多くの化合物で非常に精度良くTc/BPの値を予測することができる。約1.5倍などという統計的な数値がどれだけ意味の無いことか判ると思う。こうした処理をしてさらに合わない化合物を見るとアルコールとカルボン酸化合物で合わないことがわかる。すると、化学をやっている研究者なら、それは水素結合の効果ではないかと見当がつく。
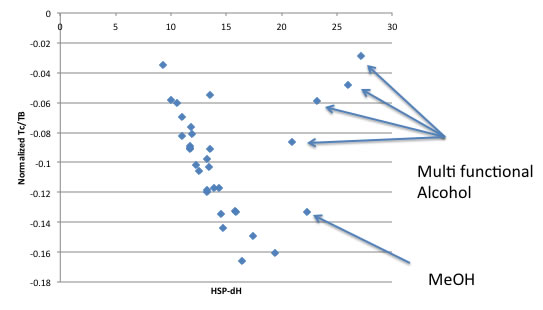
そこで、アルコールだけを取り出してさらに見てみると、2つの群があることが判る。分子中に複数のアルコールを持つ化合物と、モノ・アルコールで体積の補正を加えた後のパターンが異なる。
この事から、分子中に複数の水酸基を持つ化合物は、分子内水素結合を起こしているのではないかと見当がつく。
こうした効果を導入して推算式を構築すると、Joback法とは系列の異なった推算式が得られる。
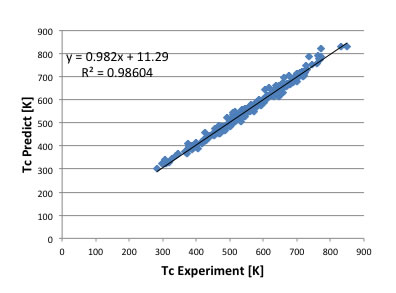
これは、原子団の定義とかは関係ないので、拡張も容易だ。
このように複数の異なった推算式を構築して新しい化合物についてはクロス・チェックをするというのは、常套手段で、その為に持っている化学の知識を総動員することができるのが化学者の化学者たる由縁だと思う。
推算式を構築する上で、利用した3つめの方法が蒸気圧法だ。
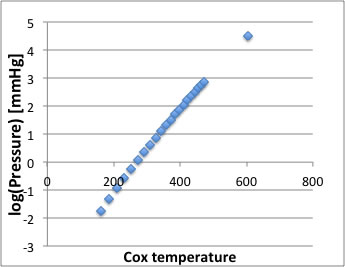
蒸気圧をCox温度に対してプロットすると、蒸気圧曲線は直線になり、その延長線上に臨界点がくる。詳しい説明はこちらにまとめたので参照して頂きたい。
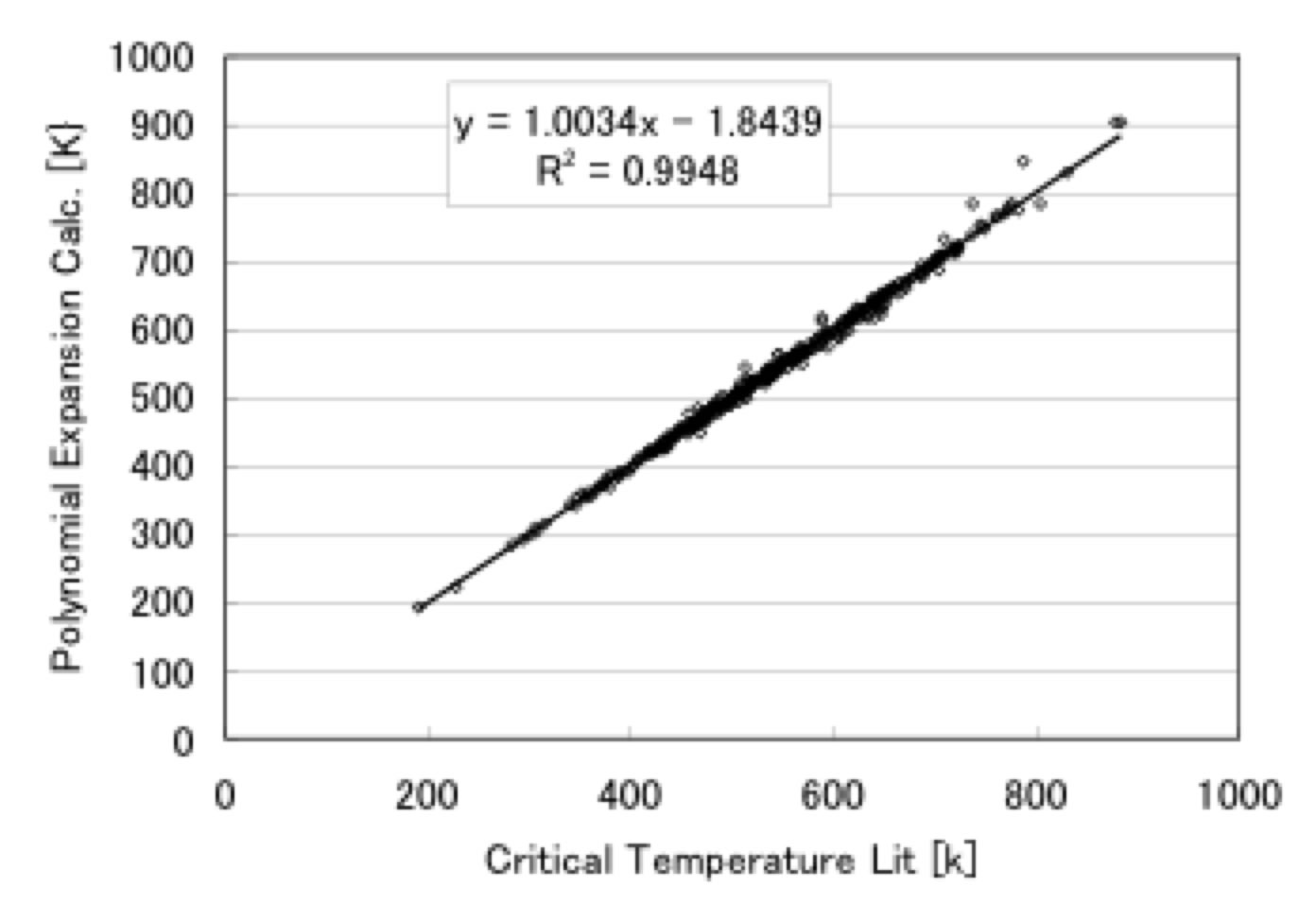
こうした方法を使っても臨界温度の推算式は構築できる。
基礎を学んだ上で市販のプロセス・シミュレータを利用するのはいいだろう。しかし中がブラックボックスでいいのなら、化学者である必要は無い。
シミュレータのオペレータ以上を目指すなら、よく理解して欲しい。
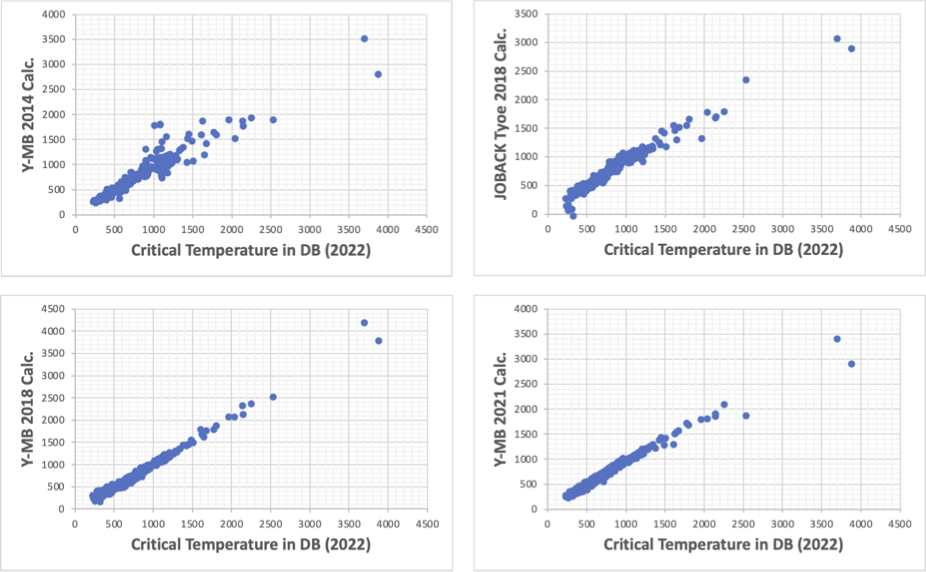
HSPiPに搭載の臨界温度推算式は改訂が繰り返されている。
臨界温度推算2022
2014,2018,2021と安定性が高くなってきている。(過学習させない取り組みが進んでいる)
物性化学トップページ
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
