2013.4.5
化学工学トップページ >
化学工学のための物性推算、シミュレーション
ある化学工学系の学会から、学会誌に寄稿してくれないかというメールを頂いた。
ニューラルネットワーク法など新規手法を用いた物性推算について書いて欲しいという事だったが、お断りした。
理由は簡単で、自分は書きたい事はPirikaのHPに皆書いてしまっているので、新たに寄稿するようなネタが無い事。
新しいネタがあったとしても、1週間もあればインターラクティブなソフトと一緒に公開できてしまう。
ページ数や紙媒体に縛られない情報発信の方を、ついつい目指してしまう事が断った理由だ。
多くの著名な先生方が執筆されるようなので、自分のでる幕でもないだろう。
たまたま、非常に面白い論文を入手した。
それを例に物性研究の実用化スピードは、世界レベルではどのくらいなのか紹介しよう。
この論文は、「拡張正則溶液モデルとWilson 式による気液平衡の相関」という論文で、山口大学工学部研究報告だ。
ネットでダウンロードできるの興味のある方は読んで見て欲しい。
簡単に要約すると、Hildebrandの溶解度パラメータを使ってWilsonの活量係数を予測する式を作り、気液平衡を推算しようというものだ。
自分は今、Hansenの溶解度パラメータをHansen先生、Abbott先生と研究しているので非常に興味がある分野の研究だ。
2013.3.18スタート
Wilson Equationというのは次のものだ。
D Gm^E /RT=-x1*ln(x1+Λ12*x2)-x2*ln(Λ21¥*x1+x2)
Λ12=(V2/V1)exp(-(λ12-λ11)/RT)
Λ21=(V1/V2)exp(-(λ21-λ22)/RT)
(λ12-λ11)、 (λ21-λ22) をウイルソン・パラメータと呼ぶ。
大文字のΛと小文字のλで混乱するので、ウイルソンのラージ・ラムダ、スモール・ラムダという言い方をする。
このウイルソン・パラメータが判れば活量係数はγは
ln γ1= -ln(x1+Λ12*x2)+x2*(Λ12 / (x1+Λ12*x2) – Λ21 / (Λ21*x1 + x2))
ln γ2= -ln(Λ21×1+x2) – x1*(Λ12 / (x1+Λ12*x2) – Λ21 / (Λ21*x1 + x2))
と計算することが出来る。活量係数が判れば、以下の式で圧力が計算できるので、気液平衡が計算できる。
P*yi = γi *xi *P^s i
P:全圧、 yi : 蒸気相のi成分のモル分率、xi : 液相のi成分のモル分率、Psi : i成分の蒸気圧、γi : i成分の活量係数
この論文では、異種分子間の分子対エネルギーを次の式を使って評価する。
λ12 = - (1 – ε12)(2/Z)(v1v2)0.5 δ1δ2
λ21 = - (1 – ε21)(2/Z)(v2v1)0.5 δ2δ1
このε12、ε21を異種分子間相互作用パラメータと呼んでいる。
Zは配位数、δがHildebrandの溶解度パラメータになる。
簡単に言ってしまえば、正則溶液モデル(Regular Solution Model: RSM)にフィティング・パラメータεを導入して拡張したという話になる。
このεは系特有のパラメータであることから、未知の溶媒ペアの気液平衡を推算しようとした場合には、実験結果からεを求めなくてはならないので、余り嬉しくない。
筆者らは系を限ればεはΔδ2に比例するとして、系ごとのεを別の論文に記載している。
これを、ハンセンの溶解度パラメータ(HSP)の技術を使って解析してみた。
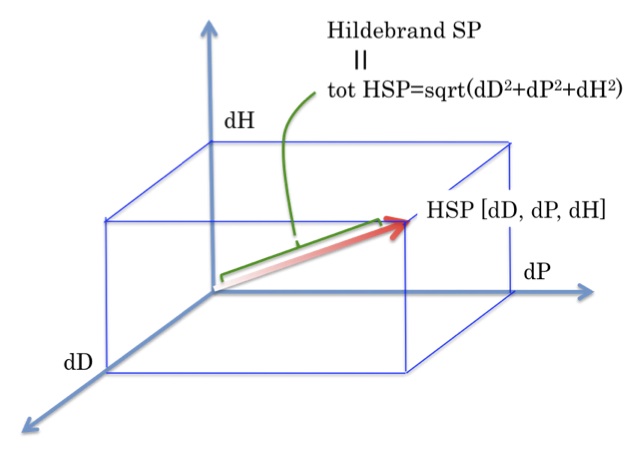
HildebrandのSP値は蒸発潜熱と分子体積からSP値= ((Hv – RT)/Volume)0.5 で計算される値だ。
データ集などにも色々値の記載がある。
あるものがあるものを溶解するかどうかをこの1次元の溶解度パラメータで評価するするのが不可能なことはHildebrand自身が認めていることで、Hansenはそれを3次元に拡張した。
dD:分散項(ファンデルワールス力に基づくエネルギー)
dP:分極項(静電相互作用、ダイポールモーメントに基づくエネルギー)
dH:水素結合項(水素結合に基づくエネルギー)
そして、この[dD, dP, dH]を3次元のベクトルと捉え、似たベクトルは似たベクトルを溶かすというのがHansenの理論だ。
このベクトルの長さはHildebrandのSP値に一致する。
従ってHSPはHildebrandのSP値を抱合し、かつ、ベクトルの向きまで含めて分子間相互作用を評価できるのでより優れた方法であるといえる。
自分はHansen先生、Abbott先生のHSPiP開発チームの一員に迎えられ、dHをさらにドナー、アクセプター(dhdo, dHac)に分割する技術、HSP値の温度依存性を解く技術を先生と共に開発した。
それを使ってこの問題を解いてみよう。
18日は関連情報を検索したり、VLEの生データを探したり、式を読み解くので終わってしまった。実際の作業は19日からだ。
3月19日
まず、(λ12-λ11)と (λ21-λ22)の値を入手する。
これは、Prediction of Ternary Vapor-Liquid Equilibria from Binary Dataという論文がネット上からダウンロードできる。
(式の幾つかが間違っているので注意が必要だ)
これを打ち込んでテーブルにするには1-2時間の時間を要するだろうが、幸い既に打ち込んだものがあった。
自分はこうしたデータはリレーショナル・データベース(RDB)を用いて管理しているので、それからテーブルを吐き出すには5分もかからない。
(HCodeというのはHansen Codeで各化合物について割り振られている。これを基準にRDBが組まれている。)
| HCode1 | HCode2 | λ12-λ11 | λ21-λ22 | Name1 | Name2 |
| 5122 | 5242 | 494.92 | -167.91 | acetone | benzene |
| 5122 | 5042 | 651.76 | -12.67 | acetone | carbon tetrachloride |
| 5122 | 5050 | -72.2 | -332.23 | acetone | chloroform |
| 5122 | 5275 | 948.29 | 234.96 | acetone | 2,3-dimethylbutane |
| 5122 | 5102 | 38.17 | 418.96 | acetone | ethyl alcohol Ethanol |
| 5122 | 5062 | -214.95 | 664.08 | acetone | methyl alcohol Methanol |
| 5122 | 5223 | 996.75 | 262.74 | acetone | pentane |
| 5122 | 5134 | 127.43 | 284.99 | acetone | isopropyl alcohol IPA 2-propanol |
このように、ウイルソン・パラメータと溶媒のリストが得られる。
次にこのテーブルに分子の情報を入れ込む。
どのようなデータを入れこむかは、先ほどの論文を参考にして、4次元のHSP値と分子体積、そして配位数Zの指標になるような分子の形状因子を入れる。
その際には4次元のHSP値と分子体積は温度の関数なので、溶媒1、溶媒2の両方の温度での値が必要になる。
自分の使っているリレーショナル・データベース、FileMaker Proはデータベースのカラムに計算値を入れる機能があるので、例えば上のテーブル1行目でアセトンの沸点をRDBから探して持ってきて、その時のHSP値と分子体積を計算したカラムを準備する。
そしてベンゼンの沸点でのアセトンのHSP値と分子体積を計算する。
(分子体積の推算にはPirikaのこちらのページを参照)
逆にベンゼンの沸点でのベンゼンのHSP値と分子体積、アセトンの沸点でのベンゼンのHSP値と分子体積を計算する。
リレーショナルDBにそのようなカラムをつけるのに1時間ぐらいかかる。
そしてウイルソン・パラメータとHSPと分子体積、分子の形状因子の入ったテーブルが手に入る。
λ12-λ11とλ21-λ22は溶媒の1と2を入れ替えた形にしてカラムを一つにまとめる。
そこまでで、正味1時間程度の作業時間になる。
得られたテーブルの構造は、λ12-λ11と
溶媒1の溶媒1の沸点での4次元HSP、分子体積 5カラム分
溶媒1の溶媒2の沸点での4次元HSP、分子体積 5カラム分
溶媒2の溶媒1の沸点での4次元HSP、分子体積 5カラム分
溶媒2の溶媒2の沸点での4次元HSP、分子体積 5カラム分
溶媒1の形状因子 2カラム分
溶媒2の形状因子 2カラム分
となる。
つまりウイルソン・パラメータを24変数から推算しようというものだ。
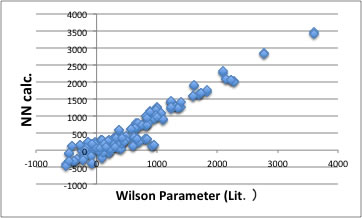
まずは、何も考えずに自作のニューラルネットワーク(NN)シミュレータで学習させてみる。
すると上のような結果が得られる。
(自分は計算にはAppleのMac Miniを使っている。6万円ぐらいのコンピュータだが、この程度のサイズの計算なら30分ぐらいで結果が得られる。)
この段階で結果が収束しないようなら諦める。
根本的に何か入力に足りないものがあるからだ。
この程度に収束するなら脈がありそうなのでさらに検討を進める。
最初にやることは、大きく外れるものを取り出してくる。
多くの場合、そのようなものは入力間違いであることが多いからだ。
また解析に使った論文をみるとウイルソン・パラータが複数記載されているものがある。
値を見てどちらを採用するかを判断する。
そのような判断をしている間に、沸点の推算式を再構築する。
自分の持っている化合物のデータベース(12000化合物)のうち、沸点のデータは7000件ぐらいある。
それから沸点の推算式を作ったものはすでにあるのだが、気液平衡を推算するような用途では無い化合物も非常に多く含まれているので、どうしても低分子側で精度が低くなってしまう。
(沸点の推算はPirikaのこちらのページを参照)
そこで自分が溶媒系に分類している化合物のうち、沸点が500K以下の化合物2881を使って沸点の推算式を再構築しておく。
(これには、化合物数が多いこと、官能基、その他の識別子で180ぐらいの変数があるので、計算に非常に時間がかかる)
料理番組ではないが、時間のかかるものは先にJobを放り込んで、最終的にプログラムを組み上げる時に全部が間に合うように作り上げるのが効率的なやりかただ。
最近のコンピュータはマルチ・コアなので並行してジョブを走らせても問題ない。
(Jobをたくさん放り込むとそれなりに排気熱がでるので、かみさんに怒られる。従って夏場には計算以外の仕事をする。書き物とか)
間違い等を修正したり、物性値を見直すのには結構時間がかかる。3月19日はここまでで終わってしまった。
3月20日は祝日なので、ゆっくり計算できる。
NNのテスト・ランではウイルソン定数を推算するのに24個の変数を使った。
次にはこの変数のどれが重要で、どの項目とどの項目が相互作用して結果に影響を与えているかを特定する作業に入る。
ニューラルネットワーク法は中身がブラックボックスになりがちでそのような解析をするのには適さない。
そこで、やはり自作のソフトで、相互作用の大きなものを抽出するソフトウエアーを利用して解析を行なってみる。
結果をみてみると、
Mol1-MCI – dHdo@BP1
Mol1-MCI – dD@BP1
Mol1-MCI – dP@BP1
が重要であることがわかる。
MCIというのはMolecular Connectivity Indexの略で分子の枝分かれ状態を記述するやり方だ。
(Pirikaのこちらのページを参照)
溶媒1のMCIが溶媒1の沸点に於けるHSP値と相互作用している事がわかる。
また、
dHdo@BP1 – dHac2@BP2 溶媒1の溶媒1の沸点における水素結合ドナーと溶媒2の溶媒2の沸点における水素結合アクセプターが相互作用していることが判る。
このような結果はHildebrandのSP値を使う限り出てこないので面白い結果だ。
この結果から24個のデータのうちどれを削り、どれを残すかを決めることが出来る。
この段階で、分子をお絵かきすると気液平衡を計算するプログラムを作る。
とは言ってもMagulesパラメータから気液平衡を計算したり、ASOG法を使って計算するルーチンはできているので、それらを流用するだけなので簡単な話だ。
1時間でできてしまう。
(ASOG法を使った気液平衡の推算はPirikaのこちらのページを参照)プログラムの名前はY-VLEという名前にする。
祭日は子どもとゆっくり遊べる貴重な時間なので、別件の大きな計算をコンピュータに放り込んで、他の仕事には反応がものすごく遅くなるようにして、強制的に人間をログオフする。
3月21日
重要な変数14個に絞って推算式をニューラルネットワークで構築する。
その間に、先の論文でやっているやり方のデータセットを構築してみる。
つまり、
λ12 = - (1 – ε12)(2/Z)(v1v2)0.5 δ1δ2
のうち、 εは未知として、(v1v2)0.5 δ1δ2を4種類を準備して、εの代わりに分子の形状因子を入れて、8種類の入力データから推算した時に収束するか?
とか、ドナー/アクセプターの相互作用を入れた時に収束するかを調べる。
3-4つジョブを放り込むとMacがうなり始める。
本命の計算が終わった段階で、昨日作ったGUIに組み込む。
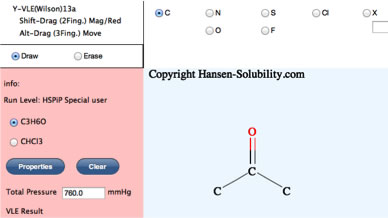
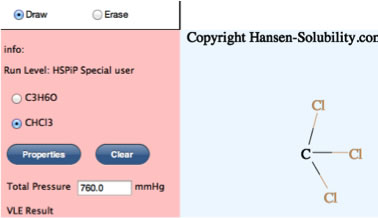
すると分子の2つの絵を書いてPropertiesボタンを押すと、分子のAntoine定数、沸点、HSP、分子体積とその温度依存性、形状因子を計算するY-VLEが出来上がる。
(Antoine定数の推算に関してはPirikaのこちらのページを参照)
沸点の計算ルーチンは昔のものをさしあたって使う。
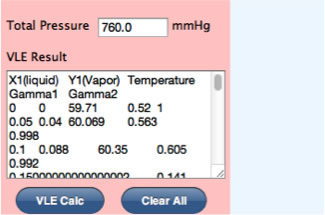
VLE Calc. ボタンを押すと、Wilsonパラメータを計算する。
結果はテキストエリアに出力されるので、全てを選択してコピーする。
それをExcelにペーストすれば、X-Y線図、活量係数などがグラフ表示できる。
アセトンークロロホルム系では活量係数が1以下になることが確認でき勇気づけられる。
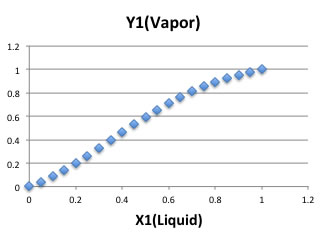
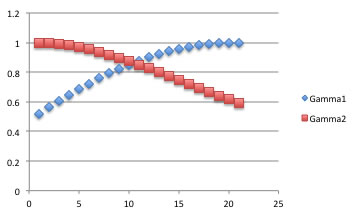
それを実験値の気液平衡データとくらべてみると
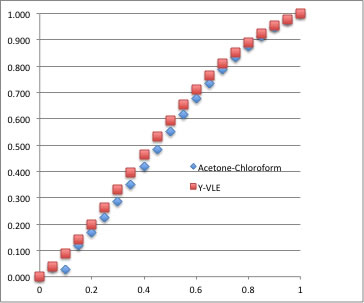
実験値を一切使わずに推算したにしてはよくあっていることが確認できる。
そして、色々な項目を変えた入力データをNNで計算し終わるたびに、幾つかのテストケースを実際にVLE計算して推算のパーフォマンスを検討する。
結果としては、最初の14変数でNNを構築したものが一番良かった。
この日、最終的に得られた推算式は、
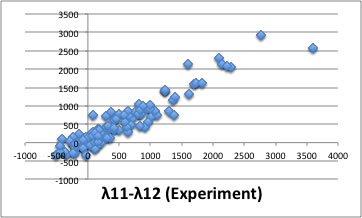
になる。
3月22日
日大の栃木先生と飲む約束をしていた。
ACSの高分子関係の雑誌のEditorから論文の査読を頼まれていたので、行き帰りの電車の中ではそれを読み、古本屋で12000円も散財してきた。
日大の栃木先生は自分がDrを取る時にお世話になった先生で、言わずと知れた気液平衡推算のASOG法の大家なので、幾つか質問をしてきた。主な疑問点は、
Λ12=V2/V1exp(-(λ12-λ11)/RT)
ウイルソンのラージ・ラムダと、スモール・ラムダで右辺にはTが入ってくるので、ラージ・ラムダは温度の関数であるはずだ。
ところがデータ集をみてみると、ラージ・ラムダの値が記載されていることが多く、しかもその温度は書かれていない。
将来プログラムを拡張しようと思い、ラージ・ラムダの値の推算という形をとった時に、温度をどうしたらいいか?が疑問点だ。
それ以外、スモール・ラムダを取ってきた今回の論文の式が間違っているような気がしたのでそれの確認だ。
その後はお決まりの栃木屋という大学のそばの中華の店でガンガン飲んで、今日も終了。
(ボトルの期限が切れる前にまた飲みに行こう)
さー、土日に全てを仕上げてしまおう。
3月23日
まず行ったのは14変数で構築したNN推算式の改良だ。
それなりに相関係数は高く、これでも十分に気液平衡を再現できてているのだが、自分の感覚では、0からマイナスの領域の推算精度をもう少しあげたい。
これは、NN法などを使って物性推算を始めた初心者が必ず陥る罠で、相関係数だけを見て議論してはダメだということがあるからだ。
つまり、推算式を構築するアルゴリズムは、重回帰も含め、誤差の自乗を最小化しようとする。
その結果として、値の大きなもの、例えば値が3000の所で、推算値が2700であったら、誤差300の自乗は90000になる。
すると値が300の所の誤差が200であってもその自乗は40000であるので、トータルの誤差を下げるには値の大きな領域の誤差を減らすほうが効率がいい事になる。
物性推算ソフトは大きな誤差ばかりに着目する。
(Antoine定数の決定法の所でもマルカート法の問題点として指摘している。)
しかし、自分は0からマイナスの領域は符号も含めて非常に重要だと考えているので、これをまず解決しよう。
自分の作ったNN解析のプログラムには、この問題を解決するアルゴリズムが搭載されているので、それを使うと大きい所の誤差の増大は多少無視してでも値の小さな所の収束を上げてくれる。
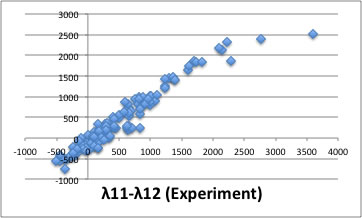
非常に効果的に改良できる事がお分かりいただけるだろう。
さらに、この結果を見ながら、どんなものの誤差が大きいかを調べる。
その際には、再び相互作用の大きなものを抽出するソフトウエアーを利用する。
すると、誤差の大きいものは、ドナー/アクセプター相互作用の大きいものであること、最初の論文の示唆する、v1δ12が重要であることが判る。そこで、それを加えた18変数でNNを構築する。
これは最終バージョンなので、NN法の持つ過学習の問題と予測性の欠如の問題を回避する機能を働かせるため、計算時間は通常の倍かかる。
(NN法の問題点に関してはこちらで説明している)
倍かかろうが、3倍かかろうが、週末は家族との時間を大事にしたいので構わない。
遊んで帰ってくると結果が出ていた。
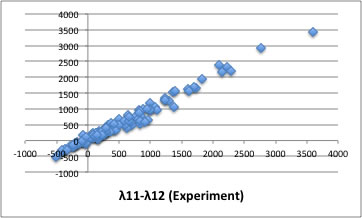
ウイルソン定数の推算式としてはいいところだろう。
その頃、沸点の推算式も出来上がっていて、
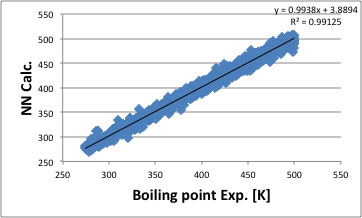
この両方をGUIソフトに組み込んで、23日は終了
3月24日
検証に移る。
実験値のVLEのデータと、分子構造のみから推算した結果とを比べてどのくらいの精度が出ているかを確認する。
これは結構時間がかかるが、子供が用があって遊んでくれないのでやってしまう。
例えばMeOH系ではこうなる。
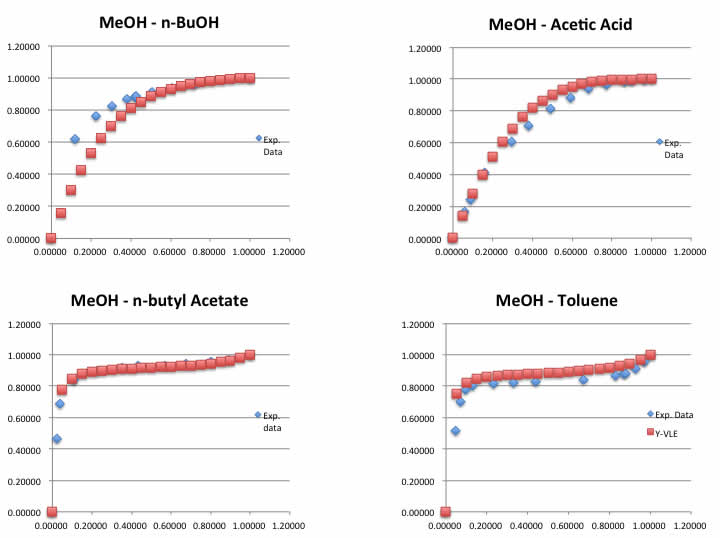
例えば、論文に書くなら、よく合うものの結果だけを書くだろう。
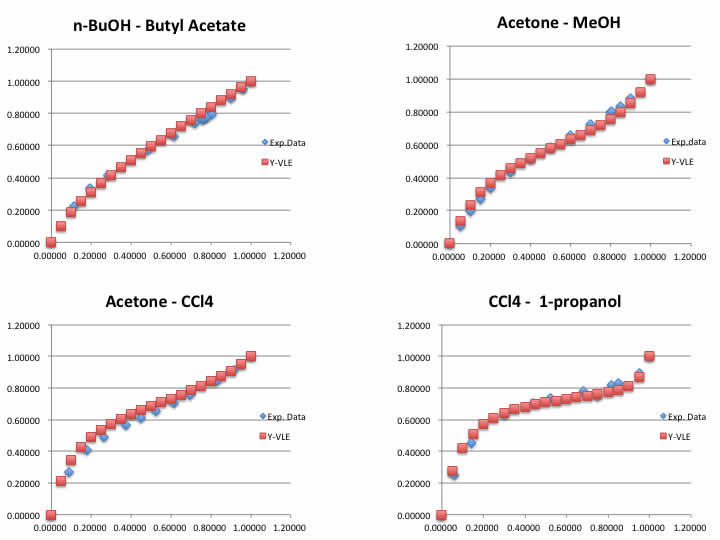
ソフトウエアーを公開しないなら、誰も検証できないので、「分子構造のみから、よく合いました」でこれでOKだろう。
誰にも文句は付けられない。
しかし、我々(Hansen先生、Abbott先生)が活量係数を知りたいのは、ハンセンの溶解度パラメータ(HSP)での混合溶媒の取り扱いをもっとエレガントにしたいからだ。
現在は混合溶媒の取り扱いは、単純に混合溶媒の体積分率だけから計算している。
それなりにはよく合うのだがさらに改良したい。
そして世界中のユーザーに使って欲しいという目的を持っている。
従ってこのモノには使ってはいけないとか、こうしたものはこういう理由で精度が低いので注意して取り扱うようにとかいう情報を提供する義務がある。
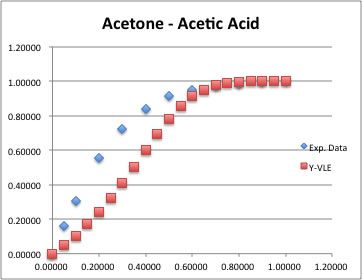
例えば、アセトン-酢酸の系では良く合っているとはとても言えない。
今回の方法は溶解度パラメータを使った方法だが、溶解度パラメータは蒸発潜熱をその基礎にしている。
(蒸発潜熱の推算にはpirikaのこちらのページを参照)
ところが、酢酸はダイマーで蒸発することが知られており、ダイマー化することで水素結合の効果が減少するため、蒸発潜熱が非常に小さくなる。
(詳しくはPirikaのこちらの記事を参照)
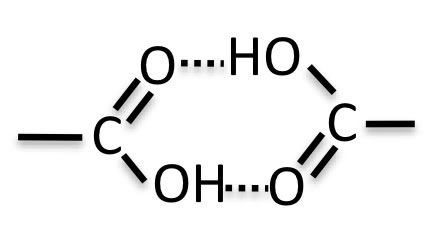
それでは、何故アセトン-酢酸の系では合わずに、MeOH-酢酸の系では合うのだろうか?
違いはアセトンは水素結合項をほとんど持たないが、メタノールは大きな水素結合項を持つ所に答えはあるのだろう。
このあたりは一般的にもよく知られていることだろうが、我々の知らない様々な特異性は他にもたくさんあるだろう。
結果を見ながら何故かを考える過程が重要だと言うのが我々の意見だ。
教育的見地からも、良く合っているものはどうでも良い。
合わないものがどうして合わないのかを教える所に意義があるように感じる。
大学でASPEN, Pro Simなどの市販のプロセス・シミュレータを授業に使っているところがある。
使い方を習ってから社会に出れば後で苦労しない、学生のアピール・ポイントになるという事なのだろうが、中身は完全にブラックボックスだ。
おそらくこのような汎用の溶媒の組み合わせは皆正しい答えを出すだろう。
(そうでなければ売れるはずがない)
すると酢酸はダイマーで飛ぶという現象を学ぶ機会を失うし、メタノールとアセトンの違いを考える機会も失う。
手抜きをすれば、その分だけ跳ね返ってくる。因果応報ってやつだ。
また、今回解析したデータの中にニトロ化合物は一つもない。
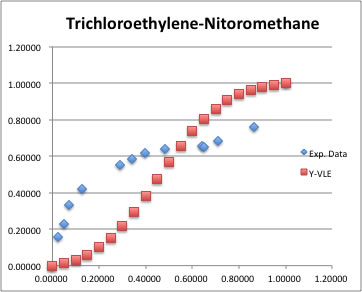
Wilsonパラメータの推算値が悪いのか、Antoine定数の推算値が悪いのかデータを拡張して検証を続けていく必要がある。
課題は残るが、分子構造のみから活量係数を予測する技術には目処がたった。
3月25日
この結果をHansen先生、Abbott先生にレポートを書いて(当然英語で)Y-VLE計算ソフトとソースコードを送付した。
すぐさま、返事が来て議論がスタートする。
一番時間がかかって、自動化できないのはこの英語のレポートを書くところかもしれない。
(当然、こうしたHPの記事を書くのも半日仕事で自動化できないのが難点だ。)
3月18日に論文を見つけ、1週間で、ソフトウエアーとレポートをが出来上がる。
我々はたった3人の(手助けする学生もいない)小さな研究グループだが、世界に伍して戦っていくには、このぐらいの研究スピードは当たり前のことだ。
タワゴト
電気電子が韓国、台湾にしてやられたのは、意思決定のスピード感の無さ。
化学も同じで、「物性研究の方向性を議論する」とか、そんな悠長な事言っている場合では無いと思う。
どう諸外国のスピードに負けない物性研究をするか?
どうやって実用レベルに持ち上げるか?
どうやって企業のニーズに応えるか?の状況にあるのだと思う。
今回は論文の解析だが、企業の方は自社の特許をこのような方法で解析され、1週間で「さらにいいもの」を作る方法を開発されてしまうことを想像してみて欲しい。
以前、東大の船津先生からお聞きした話しであるが、日本は公開特許を33万件/年、世界に公開している。
中国からは17000件/日、韓国からは55000件/日アクセスがあるそうだ。
彼らは日本の特許にアクセスして何をしているのだろうか?
日本語の勉強?
自分が横浜国大の授業で特許ネタを多用するのはこの為だ。
IT(Information technology)革命は産業革命以降の最大の生産性向上の革命と言われた。
産業革命は言わずと知れた、蒸気機関を使うことによって一人の人間の工業的生産性が飛躍的に高まった革命だ。
日本ではながらくIT=インターネット・通信と訳されていたくらいで、インターネットをを使って物を売ると楽して儲けられるよという意味に使われてきた。
今だに情報通信と訳しているくらいなので、IT企業と言えば今でもそういった意味に使われているように思える。
自分にとっては情報は化学情報で、化学情報は分子の構造式の中に蓄えられている。
その情報を自由に操れることが出来れば生産性は1000倍、1万倍になると信じている。
このようなY−VLEのシステムを、ITに長けたものが作れば1週間仕事。
自分たちのスピードレベルがどのくらいなのか問い直すきっかけになればと思う。
今までの日本の研究は将棋型だったのだと思う。
守りを固めて、相手の陣営に攻め込む。
IT時代は囲碁型、オセロ型に意識改革をしなくてはならないのだろう。 盤のどこかに脈略なく打たれる。
攻め込んだつもりがITで出口を塞がれ袋叩きになる。
オセロのように全部ひっくり返されてしまう。
電気電子の研究者は実感として感じているのではないだろうか。
おそらく、自分がこの結果を学会誌に投稿する用の原稿を書こうとしたら1ヶ月仕事になるだろう。
Wordは差し込んだ図がぐにゃぐにゃ動いて、1ページに何行、何文字の指定もMac版のWordは言うことを聞かないし。
参考文献の書き方のフォーマットはどうのこうの。
図の大きさは文字何個分でうんたらかんたら。
グラフの軸のフォーマットはこういう決まりで。。。。
そんなので1ヶ月も仕事をストップするくらいなら、そういうのに慣れた先生方に学会誌はお任せしよう。
1日がかりにはなるが英語版のページを作れば全世界から議論が舞い込んで来るのでよほど楽しみだ。
自分は数年前までは解説などを書いたりしていたが、日本人からのフィードバックはもらった事はほとんど無い。
学会誌に書いたものでも、PirikaのHPに書いたものでもフィードバックは年1件もあれば上出来だ。
日本のこうした状況だと信じられないかもしれないが、「情報を独占したければ情報を発信することだ」という一見すると矛盾する、情報学の世界一般の常識がある。
例えば今回は論文にデータは無いので、Y-VLEでもフッ素原子は入っていないが、こうしたHPを読んだ(日本以外の)研究者からフッ素を入れられないか、データはこうした論文に載っているという連絡を受ける。
今回のやり方では、こうしたファクターが抜けているので、一緒にやらないか?
分子の分割法はやはりUNIFACのものが合理的だ、この系で合わないのだけど、などなど様々な情報が集まってくる。
論文、書籍や特許から引用される。
するとさらに情報は増える。ネットの時代、情報は隠して独占するというモデルは崩壊している。
またAppleの例を挙げるまでもなく、全て自前主義は立ち行かない。
ここだけは譲れない1点を除いて他の分野の専門家と組んで仕事をする事はますます重要になるが、そうした専門家とのつながりも情報だ。
ITを利用しようとした時何が足りないだろう?
例えば今回の例のように、解析用のソフトを自前で揃えてから参入するのであれば、大手以外ではそれだけで何年もかかってスピードはかえって1/10、1/100になってしまうだろう。
先述の東大の船津先生(自分がDrを取った時の副査の先生でもある)はCACフォーラムを主催されていて、化学系の解析ソフトを配布されてもいる。
そうしたフォーラムに入会してソフトを利用させて頂き、学び、スピードアップを図るなどの施策が有効であろうが、船津先生がそういうことをやられているということも知らない(情報難民)であれば打つ手が無くなってしまう。
では、どんな化学が融合すべきなんだろうか?
Pirikaでは物性化学、高分子化学、計算機化学、化学工学そしてそれらを統合する情報化学が大事だという立場を取っている。
自分に足りないのは分析化学だろうか。30年近く前の大学のレベルで止まっている
大手企業に対してならともかく、学会は会員に対して、大局観とスピード感を持ってリードする義務があると思う。
諸外国がスピードを非常に速めているのに、日本だけ10年一昔のごとく、の施策をとっていて大丈夫なのか?
化学は日本の最後の砦だと思っているので、是非とも頑張って頂きたい。
Hansen先生からは、もっと論文書いてアカデミックなポジションを得て、学生を使ってガンガンやったほうが良いのではと助言を頂いている。
(自分の推薦状でよければ、いくらでも書いてあげると言ってくださる。)
でもHansen先生は日本のアカデミアの現状をご存じないし、スピード感もご存じない。
それにIT時代、状況は確実に変化してきている。
例えば、自分が昔から利用しているCCL(Computational Chemistry List)というWebサイトが有る。
計算機化学用のソフトウエアーがソースコードとともに公開されているので、非常にお世話になっていた。
そのサイトは、現在、ACS COMP Division がサポートを行なっている。
オンラインで世界最大の化学系データベース、ChemSpiderはイギリスのRSC( Royal Society of Chemistry)がサポートしている。
MITなどの行なっている、MOOC(Massive Open Online Course:世界中の大勢の人々が参加できるオンラインのオープン授業)は世界中から10万の受講者を集めている講座があるそうだ。
欧米のアカデミアはネット勢力との付き合い方を変える方向に確実に動いている。
PirikaがACSやAICHEからサポートされる日を夢見て、当分は現状維持を取ろうと思う。
Hansen先生には「日本は黒船が来ないと動かないから、早くノーベル賞でも取ってくれ」と言って笑っている。
今回作成した活量係数推算式はAbbott教授によってHSPiPに搭載されることになっている。
(2013.8.18、Ver.4.1に搭載されリリースされました)
Abbott教授は、ユーザーは何も知らなくても正しい結果が得られるようにソフトは作るべきだという考えをお持ちなので、使いやすいプログラムになるかもしれない。
自分は全く逆の立場で、究極のソフトは人であるので、最低限のことは学んでプログラムができる事以上の事を導き出せるようにするべきだと考えている。
毎年1回、3人で集まって開発者会議を行うのだが、Abbott教授と自分が、喧々諤々と議論を始める。
Hansen先生は笑ってみている。
するとAbbott先生の奥さんが現れ「あなたたちは仲がいいのだか、悪いのだか。Hansen先生の奥さんと買い物に行くからクレジットカードを出しなさい。あなたは荷物持ち」と割って入る。
「喧嘩ではなく議論しているだけだよ」といいながら、それでも頭を冷やしに出かける。今年も6月に行う予定だ。
2012.7.1 開発者会議の初日からこの機能の議論になった。
一部論理的なミスを指摘され、あわててAbbott教授のMacMiniを借りて再計算した。
ついでなので露点曲線も入れてグラフィック表示するようにしてみた。
それでは、Y-VLEを使って実際に計算してみよう。
そんな訳で、学会誌への投稿、講演会の講師、座談会などは皆お断りしている。異論や批判はあるだろう。HSPiPチームはそうした議論を通じてのみ科学が進歩するという立場を取っている。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
