2013.8.1
化学工学トップページ >
Solubility in Supercritical Carbon Dioxide (Ram B. Gupta, Jae-Jin Shim) CRC press. に超臨界二酸化炭素への様々な有機化合物の溶解度が示されている。
このデータに対して、ハンセンの溶解度パラメータを用いて溶解度を推算しようと(HSPiPチームのAbbott教授が)試みたが、それはうまく行かなかったそうだ。
(超臨界炭酸ガスのハンセンの溶解度パラメータについてはこちらを参照)
東北大学の研究Grが理論計算の結果と溶解性をQSARした結果を、熱物性 21[3](2007) p137-142に投稿している。
それについては2011年のYNUでの講義で説明した。
分子軌道計算の結果と相関を取るよりは、熱物性と相関を取るほうが容易に推算式を構築することが出来る。
化学工学ならでの知識を活かしてこの現象を考えてみよう。
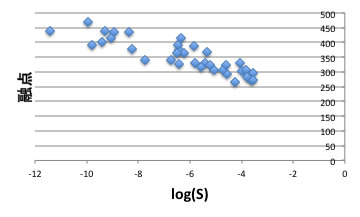
例えば化合物の融点とプロットすると、綺麗な相関がある。
すると融点が低い化合物ほど超臨界二酸化炭素へよく溶けると言える。
それは「ある化合物の表面から1分子をもぎ取るのに融点の高いものからもぎ取るのは難しそう」と考えれば納得できる。
(それにしても、例えば同じ融点400Kで100倍溶解度が異なるものがあるが…。)
試しにこの融点と溶解度の関係をGuptaの書籍の化合物に適用すると以下のようになる。
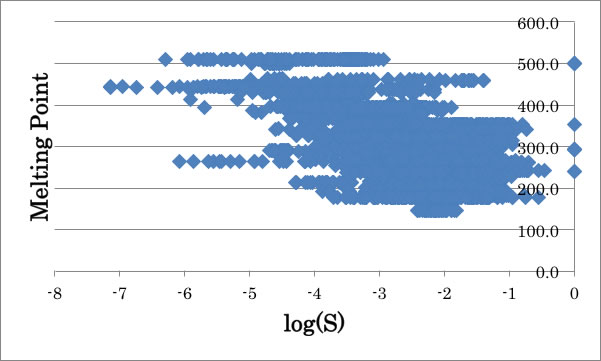
確かに大まかな相関はあるが、同じ融点でも100000倍溶解度が異なる事がある。
一番大きな違いが何かと言えば、東北大学のデータは実験値を308K、14MPaに補間し用いている。
つまり温度と圧力が同じなら化合物の溶解度はXXXXで決まると主張しているに過ぎない。
また対象の化合物も全て芳香族化合物と非常に限定された系で構築された式であるので、Guptaの400種類近い、様々な温度と圧力で測定された溶解度は再現できなくて当たり前かもしれない。
そこで、まず東北大の化合物にさらに彼らの出している特許(JPA_2000167377)の化合物を加え、YMBを用いて様々な熱物性を推算して溶解度とXXXXの相関を考える。
(XXXXが何かを考える) その後に温度と圧力の影響を考えてみよう。
YMBを使って分子の構造を描くと様々な物性値を計算する。
HSPiPに搭載されているY-MBは分子のSMILESの構造式から一括で計算することができる。
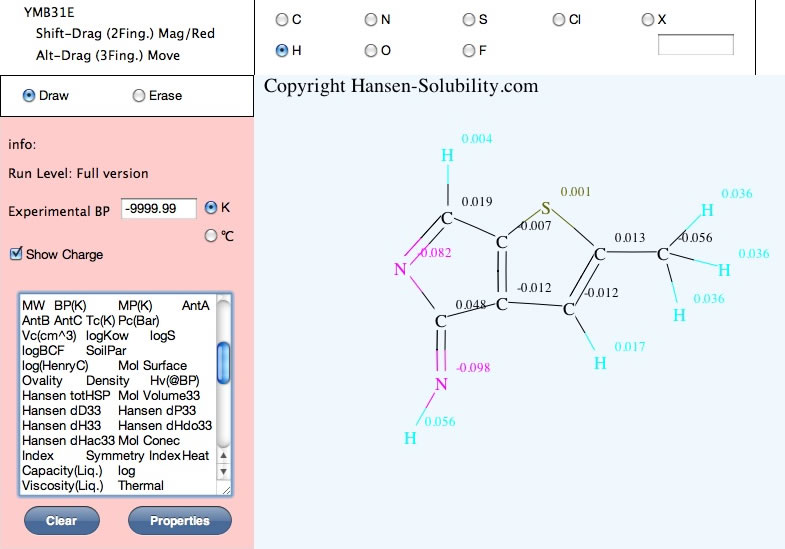
YMB12E(Chromeなどのブラウザー上で分子をお絵かきし、様々な物性を瞬間で計算するソフトウエアー 2012年授業用ソフト)
最新のYMBとVSMRの使い方はこちらを参照
企業からの訪問者はYMBではなく、HSPiPをお使いください。
各化合物の溶解度と物性値をスプレッドシートにまとめてグラフ表示してみる。
相関の高いものは次のような物性値であった。
例えば表面張力。有機化合物の表面張力が低い程良く溶解するという結果になる。
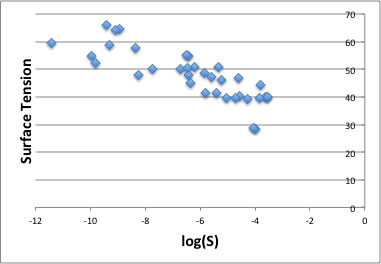
これは、超臨界炭酸ガスの表面張力が非常に小さく、超微細部への浸透・乾燥が可能であるという性質から考えて、逆に表面張力の高い化合物へは浸透しづらく溶解性も低くなっているのでないかと考えられる。
また、液滴のサイズを考えると表面張力の差が大きいと、エネルギーを下げる為に大きな球形(表面積最少)構造を取り、表面張力の差が小さいと小さな液滴になるので、このような溶解度の差が出るのではないだろうか?
また粘度と溶解度の相関をとると、粘度が低い程良く溶解する事がわかる。
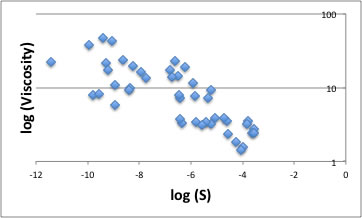
測定温度の308Kで固体の化合物は粘度は意味が無いかもしれないが、表面張力にしても粘度にしても推算値の値は、液体のまま所定の温度まで変えた時の外挿値であると理解いただきたい。
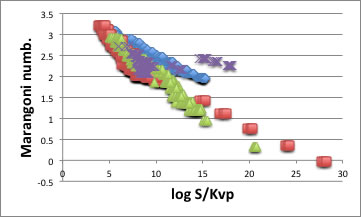
このように溶解現象が表面張力や粘度に影響を受ける場合にはマランゴニ数で整理できる可能性が高い。実際にプロットすると以下のような相関が得られる。
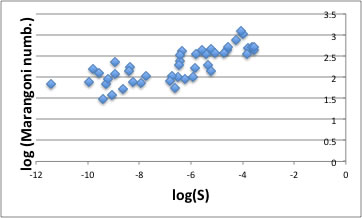
マランゴニ数と溶解度の関係
物質の表面に温度差が生じた場合、温度の高い所は表面張力が低く、温度の低い所は表面張力が高くなる。すると表面での力が釣り合うように対流がおこる。これがマランゴニ対流と呼ばれる。
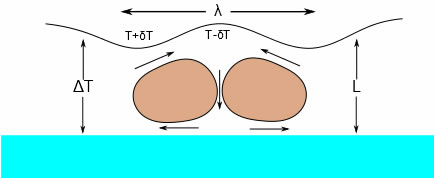
その対流の状態を決めるパラメータとして次式で表される無次元数マランゴニ数(Mg)がある。
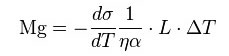
σ: surface tension, (SI units: N/m)
L: characteristic length, (SI units: m)
α: thermal diffusivity, (SI units: m²/s)
η: dynamic viscosity, (SI units: kg/(s·m))
ΔT: temperature difference, (SI units: K)
マランゴニ数の推算についてはPirikaのこちらを参照のこと。 ここでは便宜的にLとΔTを1とした時のMg値をマランゴニ数と呼ぶ。
マランゴニ数が大きいという事は、粘度が低く、表面張力の温度依存が高い、つまり対流が強い状態を示している。
その対流が大きい程、溶解度が大きい事をこの結果は示している。
最初に見いだした「溶解度は融点と相関がある」というのは融点の高いような化合物は粘度も表面張力も高いだろうから当たり前の事かもしれない。
試しに融点と表面張力の推算値同士をプロットすると次のような相関になる。
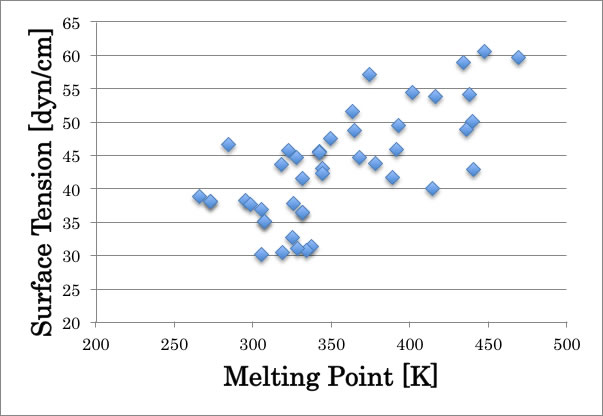
このマランゴニ数に関して日本語で検索をかけると、ほとんどすべての結果はJAXAのものだ。
宇宙空間でのマランゴニ対流の結果だ。
これは例えば地上で液体に下から熱をかけると(みそ汁の鍋を火にかけたときを思い浮かべれば良い)加熱されると液体は軽くなり上昇流がおき、表面の低温の液体は比重が重く下降流となり、熱対流がおこる。
これは液体が温度によって比重が異なるからで、重力が無ければ比重差による対流は起きない。
そこで宇宙空間ではマランゴニ対流のような表面張力の差による対流が熱対流に邪魔されずに観測する事ができる。
では、地上ではマランゴニ対流は無視できるのかというと、上の模式図のLやλ次第で、サイズがインクジェットのようなナノ・レベルになってくるとマランゴニの効果が出てくる事もある。
(YouTubeの映像、インクジェット着滴後の乾燥&コーヒーステイン現象を見て頂きたい。
コーヒーステインというのは、コーヒーの液滴が乾く時に、中央部よりも周辺部にコーヒーの濃い模様が現れる現象のことだ。
これはマランゴニ対流で説明される。)
マイクロエマルジョンのように液滴が液体に分散しているような一種の無重力状態、金属やカーボンのナノ・マテリアルが溶媒に分散している状態などではマランゴニ数で整理すると理解できる事も多々ある。
超臨界炭酸ガス中での、マランゴニ対流を検討した例は、自分は知らないが、豊田中央研究所の福嶋喜章博士の研究に非常に興味深いコメントがある。
引用させて頂くと「全体が均一な溶液系でありながら、分子の周囲の状況が常に変化し大きなゆらぎを実現している不均一な状態も同時に実現しているのが超臨界流体の特徴である。このような「ゆらぎ」により、液体と気体の長所を同時に実現出来る溶媒と言える」 といっている。
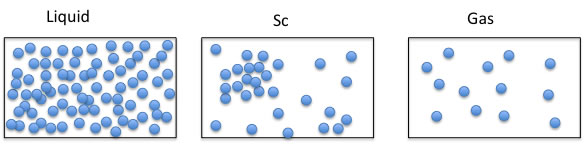
模式図を書くと上のようになるのであろうか?
液体状態では、分子同士の衝突確率は非常に高いが、分子の速度は速くなれない。
気体状態では分子の移動速度は非常に早いが衝突確率は低い。
超臨界状態では雲や霧のように集合して密度の高い部分と薄い部分が存在し、それは固定されたものは無く雲や霧のようにゆらいでいるものなのだろう。
薄い部分では分子の移動スピードは速く、濃い部分に衝突するとビリヤードのブレイクのようにはじき飛ばし、新しい部分にまた濃淡を作り出すのかもしれない。
そのような超臨界状態の中に溶質の液体がいた場合にどうなるだろうか?
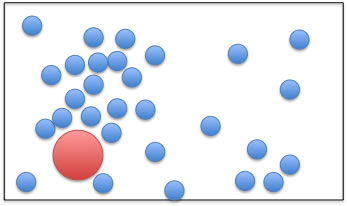
溶質の液体(赤色)が濃い部分と薄い部分に接触している2つの領域が存在すると、分子の運動エネルギーの授受にアンバランスが起き表面張力の差が生じ、溶質液滴内部にマランゴニ対流が生じるはずだ。
そしてその対流の度合いで溶解性が変わっているのではないだろうか?
それでは、ここから先はGuptaの書籍にあるデータで見て行こう。まずマランゴニ対流という対流を起こすためには測定温度で液体でなければならない。
固体でもScCO2に溶解すれば液体とも考えられるが、複雑になるので300Kで液体のものだけを対象にする。
マランゴニ数の計算には所定の温度での物性値を推算して計算するので、温度の効果は織り込み済みである。
それでは圧力についてはついてはどうであろうか?
これまで、どの論文、書籍を見ても詳細に記載されているのを見たことがないが、こと液体の超臨界炭酸ガスへの溶解に関しては非常に面白い挙動がある。
炭酸ガスの臨界点 (31.1 °C、74 bar) であるので、多くの溶解実験は温度、304.25K以上、圧力74bar以上で行われている。
しかし、Guptaの書籍にあるデータには、ものによると74bar以下の圧力での溶解度のデータが記載されている。
酢酸では、次のように圧力に対して下に凸のグラフになる。
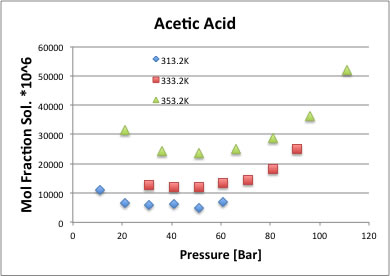
アセトンの場合にも同じように下に凸になる。
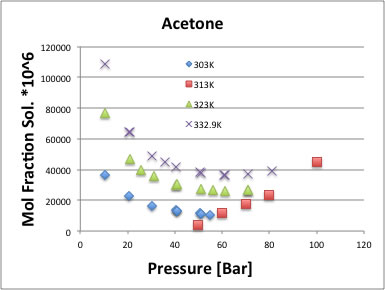
ほとんどのデータは60Bar以上の圧力で溶解度を求めており、低圧まで測定している例の方が少ないが、実験値のあるものは皆下に凸になっている。
温度が低い時ほど下に凸の最低値は低圧側にシフトする(40Bar付近)。
温度が高いほど最低値は高圧側にシフトする(70Bar付近)。
温度が高いと溶解度は上がる。それは通常の溶媒に対する溶解度と同じなので理解しやすいが、圧力に対して下に凸になる理由がわからずに2日2晩悩み続けた。
福嶋先生の言う”ゆらぎ”ではないかと密度とプロットしたりしたが無駄だった。曲率も溶質によって異なるがその理由もわからなかった。
半分くらい諦めかけた時やっとその理由が解った。
圧力が低いほど溶解度が高くなるのは、液滴からの蒸気圧が溶解度に影響を与えている。
温度が同じなら蒸気圧は一定であるが、液滴の外、ScCO2の圧力が高くなれば高くなるほど液滴から外に飛び出る分子は減る。
従ってYMBを使って溶質のAntoine定数を求め、測定温度での蒸気圧を求める。
それを測定圧力で割ったものと溶解度を(測定圧力70Bar以下のデータに対して)プロットしてみる。
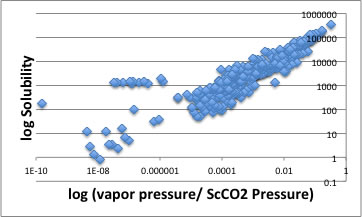
すると溶解度1000のあたりに例外がある。これらはフタル酸エステルである。これらの化合物は高分子の可塑剤に使われる化合物で沸点が非常に高く、従って蒸気圧も低い。
蒸気圧以上によく溶解するので例外になっているのだろう。
それ以外のデータに関してはおおよそ直線関係にあるので、0-70Barの範囲で圧力が増すに連れ溶解度が下がるのは液滴から蒸発しにくくなった為と理解してよさそうである。
それでは下に凸の右側で溶解度が高くなるのはどうしてだろうか?
圧力はさらに高くなるので蒸気圧による溶解性は漸減するはずである。
そこでlog SolubilityをKvp=(Vapor Pressure/ScCO2 Pressure)で割った値と、化合物の物性にどんな相関があるのかを調べてみた。(つまり、温度の効果は蒸気圧と各物性値の温度依存性でキャンセルして、圧力の効果はKvpでキャンセルして、正味の溶解性は化合物のどんな物性と相関しているのかを調べてみた。)
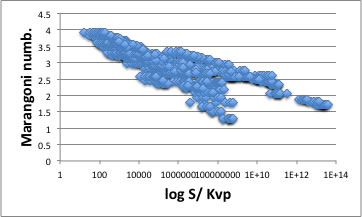
すると、最も高い相関を示した物性値はマランゴニ数であった。
よく見ると線が何本かあるように見える。そこで該当する線に溶質をグループ分けしてみる。
アルコール類
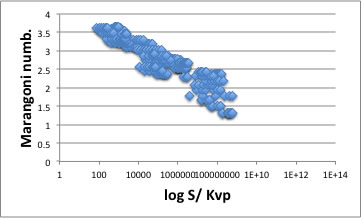
Acid類
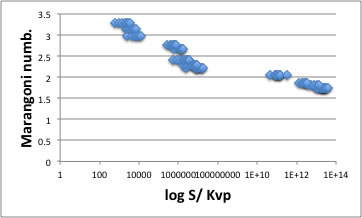
フタル酸エステルなど例外
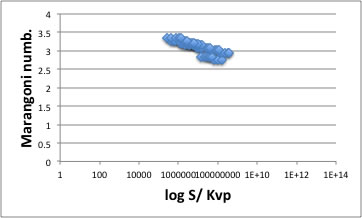
それ以外の溶質全て
重ね合わせると以下のようになる。
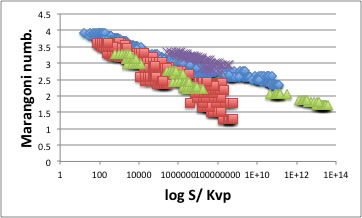
つまり、化合物の超臨界炭酸ガスへの溶解性は、温度、圧力をキャンセルすればマランゴニ数で決まっている事がわかる。
カルボン酸やアルコールのような水素結合性の化合物が線に載らない理由は、マランゴニ数の推算精度がまだ低いからなのか、本質的に読みきれていない因子があるからなのかは今のところ分からない。
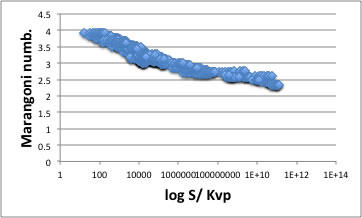
マランゴニ対流と言うからには、液体でないと対流を起こさないので、液体だけを選んできて解析したが、残りの300Kで固体の化合物の溶解度を同様に処理して見ると以下に示すように液体と同様マランゴニ数で整理できる事がわかる。
マランゴニ数は固体の場合1桁小さくなり、溶解度も小さくなるが傾向は同じである。
Benzyl alcohol (BP:478K)を例に取ると全体のイメージは次のようになると考えている。
圧力が低い領域では、蒸気圧に相当する分子が溶解している。
温度が沸点に近づくに連れ圧力が低くても溶解度は非常に高くなる。
温度が同じまま、圧力が上がってくると溶解度は下がり続ける。
それは溶質の分圧が減少することで説明される。
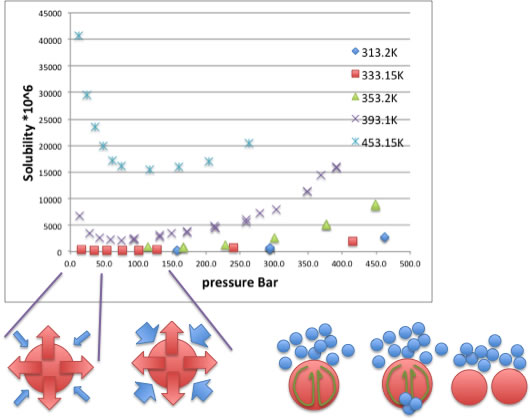
その間、液滴の中では、その時の温度での、密度、表面張力、粘度、熱伝導度、熱容量から決まるマランゴニ数に従って対流が起きている。
対流が大きいほど溶解性は高くなる。その理由として考えられるのは、圧力が高くなると対流の隙間にそって炭酸ガスが液滴に侵入して液滴を分断させ、表面積の増加が起ているのではないだろうか?
そして表面積の増加に従って溶解度が上昇する。
この考え方で、”圧力が高くなると液滴を分断”のところが確証が無い。
超臨界晶析などを行った場合には、出来る粒子径は液滴のサイズを反映していると考えられるので、そうした結果が出てくるのが楽しみだ。(データをお持ちの方がおられましたら教えてくだされば幸いです。)
超臨界抽出ではエントレーナーにエタノールを少量加えたりする。
劇的に溶解度を変える効果があるが、これは溶解度パラメータなどでは説明できない。
エタノールがあることによって表面張力が劇的にかわり、マランゴニ対流が大きく変化するのかもしれない。
以上、蒸気圧、密度、表面張力、粘度、熱伝導度、熱容量など化学工学で慣れ親しんだ物性値を使うことで、超臨界二酸化炭素への有機物の溶解現象を考えてみた。
自分の系に最適な、温度や圧力、エントレーナーの選択に様々な指針を与えるのではないかと思う。
医薬品などを超臨界晶析する場合、粒子表面の形状がその後の溶解性に影響を与える。
マランゴニ対流がきれいにかかった状態で脱溶媒和が進めば表面がつるつるの球状の粒子が得られるかもしれないが、溶解性に対しては表面積が少ない分不利かもしれない。
どんな溶媒で、どんな温度、圧力で晶析するかを考える上で重要な情報を与えてくれるだろう。
LiB用の触媒の晶析に対しても同様かもしれない。こうした重要な無次元数:マランゴニ数についてはよく勉強しておこう。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
