2018.6.20
10. 分子構造論(液体構造論)から見た蒸発現象
様々な液体分子の蒸発
身近な沸騰現象としてはキッチンを中心とした水の沸騰を思い浮かべる事が多いでしょう。しかし,家庭内であっても様々な化合物が沸騰しています。エアコンや冷蔵庫の中では,主にハロゲン化合物の冷媒が沸騰と凝縮を繰り返しています。バブルジェット・プリンターの中では,アルコール/エステル/エーテル系の化合物が沸騰しています。殺虫剤や整髪料のスプレー缶の中では液化天然ガス(LNG)が沸騰しています。カセット・コンロ用のボンベやライターの中ではブタンやイソブタンが沸騰しています。こうした水以外の化合物の蒸発・沸騰を考えて見ましょう。家庭内で起きる別の沸騰,そう,頭から湯気を出して沸騰するレベルが,お父さんとお母さんで異なるように,化合物によって蒸発・沸騰現象は異なって見えます。そうした時に大事なのは化合物によらない(お父さんであるかお母さんであるかによらない)普遍的な基準を持つ事でしょう。沸騰現象を考える前に,まずは沸騰の前段階,分子構造論から見た蒸発現象を見ていきましょう。
蒸発現象
水に限らず,ある液体があった時に,液体の中では分子が運動し,お互いがぶつかり合っています。その様子を花粉の動きで観察したのがロバート・ブラウン(1827年:ブラウン運動)です。気体と違って液体は非常に混み合っていて,少しでも動くと他の分子に衝突します。衝突によって,液相からはじき出された分子は気相に飛び出します。そうした気体が壁に衝突する事で圧力が観察されます。これが蒸気圧です。液体の温度を高くしていくと,分子の運動が激しくなり,気相に飛び出る分子も多くなります。この蒸気圧が大気圧と等しくなった点を標準沸点と定義します。そこで,高い圧力のかかる深海では水は100℃では沸騰しませんし,大気圧の低い高山でラーメンを煮ても(水は100℃以下で沸騰するので)生煮えになってしまいます。怒りっぽくなっているお母さんを「低気圧が来ているから注意しよう」という表現を使うのはここから来ているのかもしれません。
温度を変化させた時に,蒸気圧がいくつになるかを示す,様々な蒸気圧式が開発されています。古くは1850年に発表されたClausius-Clapeyron式,1888年に発表されたAntoine式,1923年に発表されたCox線図などです。さらに,拡張Antoine式, 5定数蒸気圧式とどんどん複雑化して行っていますが,複雑化していくにつれ化合物特有の定数に意味は無くなっていき,単なるフィティング・パラメータになっていきます。Wagner式はファンデルワールスの状態方程式の精度を高める為に第2ビリアル係数を組み込んだ式で、汎用溶媒の蒸気圧式として使われる事は多くありません。基本としては,定数の物理化学的な意味合いが明確な最初の3式を押さえるのが大事になります。
① Clausius‐Clapeyron式 1850年
ln(Pvp)=A-B/T B=ΔHv/RΔZv
② Antoine式 1888年
log(Pvp)=A-B/(T[℃]+C)
③Cox線図 1923年
log(Pvp)= A- B/( T[℃]+230)
④ Extended Antoine Equation
log(P[bar])=A-B/(T[K]+C-273.15)+0.43429Xn+EX6+FX12
⑤ 5定数蒸気圧式
log P = A + B/T + C*logT+DT+ET2
⑥ Wagner Equation
ln Pvpr = (aτ + bτ1.5 + cτ3 + dτ6 )/Tr (τ=1-Tr)
①-③の式は,ほぼ同じ形の式である事が解ると思います。Clausius-Clapeyron式では,温度の補正項は無く,Antoine式では化合物特有の定数(Antoine C定数),Cox線図では230という定数で,温度項を補正しています。
定数BはClausius-Clapeyron式で定義されているように, B=ΔHv/RΔZvでΔHv:蒸発潜熱(単位はKJ/mol, モルあたりのエネルギーである事に注意してください),R:気体定数,ΔZv:圧縮係数の差(狭い範囲で一定)ですので,定数 Bは蒸発潜熱のみの関数になります。
温度の補正項
先ほど温度の補正項として,Antoine式では化合物特有の定数(Antoine C定数),Cox線図では230を使うと書きましたが,Cox線図で用いる230という値は,炭化水素化合物の平均値の値になります。炭化水素以外では値が異なってきますが,この補正項の意味合いを考えて見ましょう。例として極性の異なる,n-Butanol, Ethyl Ether, Diethyl Amine, Diethyl Sulfide, N,N-Dimethyl acetoamide, Heptaneの6化合物(表1)を選んでみます。これらの化合物の蒸気圧を温度に対してプロットすると図1に示すように,化合物特有の曲線を示します。
表1. 化合物のAntoine定数と蒸発潜熱

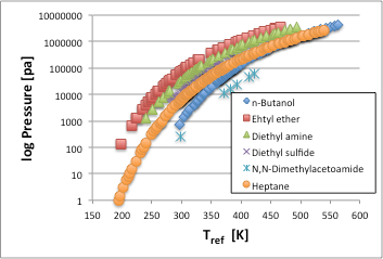
図1. 化合物特有の蒸気圧曲線
この横軸を,Antoine式に従って,温度から1/(Tref[℃]+Antoine C)に変換してみると,図2のように各曲線はみな直線になります。つまり,温度の補正項は,蒸気圧曲線を蒸気圧直線に変える為に導入されたパラメータである事がわかります。
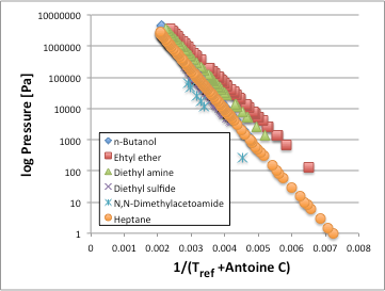
図2. 温度の補正項を加えた蒸気圧直線
アルコールやアミド化合物など極性の高い化合物は,Antoine C定数が小さくなります。これは,1/(Tref[℃]+Antoine C)で見た時に,ある化合物に同じ温度を与えても,極性化合物はAntoine Cが小さい分,分母が小さくなることを示しています。蒸気圧に対してはこの項はマイナスで作用しますので,極性化合物は同じ温度をかけても,分母が小さくマイナスに作用して蒸気圧が低くなる事を示しています。つまり,極性化合物は分子間力が高く,分子会合を起こしやすく,蒸気圧曲線の曲率が高くなり,曲率を解消するための補正項がAntoine C定数だという事がわかります。この効果は極性だけで決まるのでは無く,分子が大きくなれば,その分会合性が高まるので,Antoine C定数も小さくなります。
蒸気圧直線の傾き
それでは,図2の蒸気圧直線で,各直線の傾きは何を示しているのでしょうか?
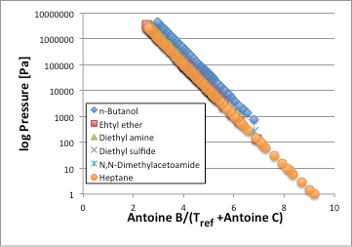
図3. 換算温度と蒸気圧直線
横軸をさらにAntoine B/(Tref[℃]+Antoine C)に変換してみると,図3のように各直線はアルコールでは少しずれますがほぼ完全に一致します。この事は,換算温度(Antoine B/(Tref[℃]+Antoine C))が一定であれば,化合物の種類によらず蒸気圧は一定になる事,換算温度の変化に対する蒸気圧の変化も化合物の種類によらず一定になる事を示しています。
このAntoine Bと沸点における蒸発潜熱(J/mol)はClausius-Clapeyron式の定義にもありますように高い相関があります。(図4)
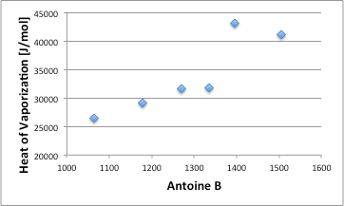
図4. Antoine B定数と蒸発潜熱(J/mol)の関係
つまり,分子にとっての温度は,Antoine B/(Tref[℃]+Antoine C)であって,地球(人間)の基準温度25℃は何の意味もないという事です。極性溶媒が高い分子間力を持ち,それを撃ち壊すには高い蒸発潜熱を必要とし,会合を壊すのに多くのエネルギーを必要とするとしても,換算温度Antoine B/(Tref[℃]+Antoine C)で見れば,液相から気相に飛び出し,壁と衝突して圧力として観測される値は一定になる事を示しています。沸点が高いという表現は,地球(人間)の基準温度25℃よりも高いだけで,沸点を換算温度で見ればどの化合物でも同じである事を示しています。
蒸発潜熱
蒸発潜熱とは液体を気体に変化させる為に必要な熱量のことです。この蒸発潜熱の値は気化させる温度,圧力に依存し,例えば水の場合,飽和蒸気圧(32hPa),25℃における蒸発潜熱は2442KJ/kgですが,1気圧100℃における蒸発潜熱は2257KJ/Kgと1割近く減少します。標準沸点では液体の蒸気圧は1気圧となり,沸点では液体が残っている間には加えた熱量は液体の温度上昇には使われず,蒸発のみに使われますので,安定的に蒸発潜熱を測定できます。そこで,蒸発潜熱の実測値は沸点のものが一番高精度になります。蒸発潜熱の単位はKJ/Kg,もしくはKJ/molを使います。化学系ではKJ/molを使う事が多いのですが,熱を仕事に変えるような分野ではKJ/Kgを使う事が多いようです。蒸発の分野では,蒸気圧式ではKJ/molとして扱いますが,水を蒸発させてタービンを回す仕事に変える時にはKJ/Kgで扱うので注意が必要です。この蒸発潜熱(KJ/mol)と化合物の沸点の間には有名な関係式,Trouton’s Rule(トルートンの通則:1884年)があります。
ΔHvap=88*Tboiling
沸点では,気相と液相が平衡にあるので,1molあたりの蒸発ギブスエネルギーはゼロになります。ギブスエネルギーの定義,G=H-TSから沸点では(G/Tbp)=(H/Tbp) – S=0となります。
そこで,Trouton’s Ruleに従う液体の蒸発エントロピーは88J/(mol・K)になります。そこで沸点と沸点における蒸発潜熱を様々な化合物に対してプロットすると,図5に示すように,ほぼ炭化水素化合物(HC)の直線とほぼ同じになります。
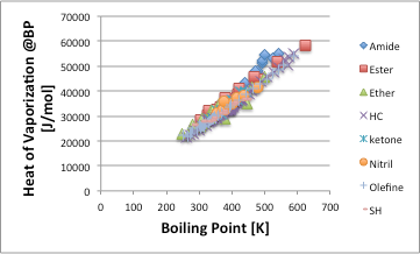
図5. Trouton’s Ruleに従う溶媒群の沸点と蒸発潜熱の関係
分子の大きさや官能基の種類に関わらず,蒸発のエントロピーが一定になるというのは不思議に思えるかもしれません。これは,つまり,分子が大きくなったり,極性の官能基が導入されて蒸発潜熱が高くなると,それにつれて沸点も高くなるので,その比率は何時も同じ88J/(mol・K)になるという事を示しています。このような比例関係にある溶媒群をHildebrandは正則溶液(1929年)と名付けました。
水やアルコールなど水素結合を作る化合物は,水素結合の秩序だった構造を持つ為,エントロピーが低く(乱雑さが小さい),気体という乱雑な状態になるには余分なエントロピーが必要になる為88J/(mol・K)より大きなエネルギーを必要とします。
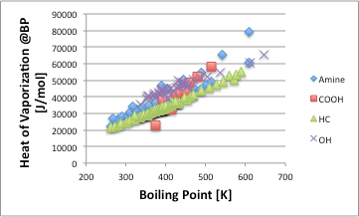
図6. 非正則溶液の沸点と蒸発潜熱の関係
そこで,図6に示すように炭化水素化合物(HC)のラインよりも高い蒸発潜熱の値を示すようになります。特異的なのがカルボン酸を含む化合物で,分子が小さなカルボン酸化合物は,分子間水素結合(ダイマー)を作って蒸発します。極性基がある意味中和されているので,非常に蒸発しやすい化合物になっていますが,系中にほんの少量でも水が存在するとダイマーが解離するので物性が大きく変化します。完全に無水の氷酢酸は,冬場には凍ってしましますが,お酢が凍らないのはその為です。正則溶液とそうでないものを分けて考えるには,分子の大きさや官能基の種類だけでは十分ではありません。弱い相互作用でも,分子中に複数の官能基を持つ場合には正則溶液からは外れる溶媒になります。水素結合が3次元的に広がりを持つかであるとか,ドナー・アクセプター相互作用,電荷移動相互作用,π-πスタッキングの相互作用、疎水場相互作用など分子間には様々な相互作用が働きます。それらを全て分離して個々の分子間力に分割することは容易ではありませんが,分子間力のトータルは,蒸発潜熱などの実測値として観察されます。
この熱量が潜熱と呼ばれている理由ですが、熱を加えているのに温度が変わらず、見かけ上消えてしまった熱量だからです。そこで気体が液体に戻るときには潜熱と同じ量の顕熱が回収されます。これをうまく使ったのがヒートテックなどに使われる暖かい下着です。皮膚からは常に水蒸気が発散されています。水蒸気は気体なので潜熱を持っています。そこで、肌着の皮膚に接する面で液化させてあげれば、顕熱が回収できます。液化された水は繊維の毛管現象で下着の外側に運ばれ、そこで蒸発または液体として滞留します。肌着自体の断熱性が高ければ肌着の外側で蒸発潜熱が奪われても体感気温的には問題ないのです。非常にクレバーな商品のように思うかもしれませんが、化学工学でも古くから使っている技術です。スーパーコンピュータのヒートシンクや石油のパイプラインの加熱、最近ではビル室内の廃熱処理に使われるヒート・パイプがそれです。金属のパイプに温度域に合わせた低沸点媒体を少量詰め、毛管現象を促す金属の網を入れ、封じたパイプです。その一端を熱源に接するとパイプの中で蒸発が起き、熱源から蒸発潜熱を奪います。その気体がパイプのもう一方の端で冷やされると液化して顕熱を与えます。液体は毛管現象で熱源に戻る,を繰り返します。ヒートテックと同じですね。
人間は汗や皮膚からの水分の蒸発で体温をコントロールする生き物です。ヒートテックが暖かく感じない人は、もしかしたら乾燥肌で水分の蒸発が少ないのかもしれません。
ちなみに、いわゆる汗は毛根の下にある汗腺から出るもので、毛の生えていない部分からは出ません。従って手の平からは汗は出ません。透明のポリエチ製の手袋をしていると曇ってくるのがわかります。そこで水分が蒸発しているのは確かだとわかります。しかし無味無臭の脂っ気なしの水です。毛根から出る汗は皮脂腺から出る脂質分やにおい成分を含んでいます。そうすると不思議に思いませんか? あの犯罪捜査で使われる指紋の事です。手のひらからは水しか出ていないなら、指紋がついても蒸発したら何も残らないはずです。実はその通りなのです。手のひらからは脂質分は出ないのですが、手、特に指は人間の器官の中で一番良く動いて、髪の毛を触ったり鼻をなでたりするので脂質分が付着してそれが指紋として残るのだそうです。そこで、指紋の形だけでなく、脂質分を調べると女性用、男性用の化粧品の成分が検出されたりするので年代やら,かなり人物像が絞り込まれるそうなので気をつけましょう。(何を?)さらに脱線すると犬は、あれだけ見事な毛皮を着ているのに汗をかきません。そこで一緒に運動をした後、長い舌を出して息をする事によって体温を調整しています。息苦しいからではありません。間違っても運動の後のサウナに犬をお誘いするのはやめましょう。
Antoine A定数の解釈
Antoine B=蒸気圧直線の傾き,Antoine C=蒸気圧曲線の曲率と比べ,Antoine A定数の物理化学的意味づけは難しいものがあります。Antoineの蒸気圧式の定義から,蒸気圧が1mmHgであるときの温度をT1mmHgとすると,
log(Pressure)=log(1)=0=Antoine A – Antoine B /(T1mmHg + Antoine C)
となるので,Antoine A = Antoine B /(T1mmHg + Antoine C)となります。
このT1mmHgが分子の基準温度になり、温度に対する感度がAntoine BとAntoine Cで決定されるのです。一般的に,化合物の融点を正確に予測することは非常に困難です。単に分子間力の問題だけでなく,分子の形状や,パッキングのしやすさなどが大きく影響するからです。同様の理由で溶媒の3重点(固体,液体,気体が共存して熱力学的平衡状態にある温度と圧力)を予測するのも非常に困難です。それに対して,分子の運動エネルギーが1mmHgの蒸気圧に相当する温度T1mmHgが,蒸気圧の実測値数点から得られるAntoine定数から決定できるのは,非常に有用ですし,この点は3重点に近い値であると考えられます。後に述べる対応状態原理は,その基点を臨界点に置きますが,臨界点の性状は気体に近くなります。液体の物性を考察する場合には,(T1mmHg, 1mmHg)を基点に考える方がより合理的と言えます。
蒸気圧式の適用範囲
蒸気圧式は実測の温度,圧力の複数の実験点からフィティングによって決定される為,適用範囲が実験点の温度範囲として示されるのが普通です。ところが,あたかも物理定数かのように,温度範囲を示さずに使われる事も多いので注意が必要です。沸点近傍までの低圧の実験値から作成されたAntoine定数と高圧の実験値から作られたAntoine定数では,値は別物になると考えた方が良いです。特に極性化合物では「Antoine C定数を決定する曲線の曲率」をとる範囲が変わるので値が大きく変化します。沸点以上臨界温度以下の蒸気圧に限っては,Coxの線図法(温度目盛りを線図によって決定)の方が高精度になる場合が多いようです。こうした線図法はコンピュータが発達する以前はノモグラム法として化学工学の領域では多用されてきました。こうした技術が失われるのは残念としか言いようがありません。Cox線図法については筆者のHP,
https://www.pirika.com/JP/ChemEng/Cox-VP.html,
で詳しく説明していますので,興味のある読者は参照していただきたいと思います。
Antoine 定数の決定法
Antoine定数の決定法は多くの場合、修正マルカート法という非線形のフィティング法で決定されます。式の形自体が非線形な式なので、実は解は無数にあります。例えば著名な便覧に記載されているデータを表の2,3にお示ししましょう。
表2 便覧に記載のAntoine定数
| 化合物 | Antoine A | Antoine B | Antoine C |
| o-ブロモトルエン | 6.90265 | 1510.203 | 194.016 |
| m-ブロモトルエン | 9.69527 | 3794.253 | 374.001 |
| p-ブロモトルエン | 9.57616 | 3799.420 | 383.762 |
表3 便覧に記載の圧力と温度
| mmHg | 1 | 5 | 10 | 20 | 60 | 200 | 400 | 760 | |
| o-BT | ℃ | 24.40 | 49.70 | 62.30 | 76.00 | 100.00 | 133.60 | 157.30 | 181.80 |
| m-BT | ℃ | 14.80 | 50.80 | 64.00 | 78.10 | 104.10 | 138.00 | 160.00 | 183.70 |
| p-BT | ℃ | 10.30 | 47.50 | 61.10 | 75.20 | 102.30 | 137.40 | 160.20 | 184.50 |
違いはo-,m-,p-体の違いだけですが、o-体だけAntoine定数の値が大きく異なります。蒸気圧の値に特段違いはありません。つまり、同程度な精度の解は無数にあり、便覧やデータ集に記載されたAntoine定数は単なるフィティング・パラメータで物理化学的な意味は無いという事です。それを避ける為には初期値を工夫し、誤差の取り方を含め最適な解析ソフトを開発する必要があります。詳しい事にご興味があれば筆者のHPを参照頂ければと思います。私の開発したAntoine定数は、フィティングの精度よりも物理化学的意味合いを重視した値になっているので、単純に正確な蒸気圧を知りたい場合には使うべきではありません。蒸気圧のデータがあれば,物理化学的に意味のあるAntoine定数を決定するWebアプリが,筆者のHPに置いてあるので使って見ていただきたいと思います。
様々なデータソースからAntoine定数を収集する際に気をつけなくてはならない事があります。同じAntoine定数であっても、式の形が複数あります。
log (P) = A – B /(T+C) P: mmHg, T: [℃]
を私は採用していますが、logではなくLn(自然対数)、PがmmHgでなくKPa、Tが℃でなくKelvin単位などのデータが混在しているので、必ず沸点を入れて計算し、大気圧になるか確認する事が大事になります。
私の使っているmmHgは、今では誰も使っていないと思いますが、ご容赦ください。1800年代までさかのぼる、化学の歴史を踏まえて、構造—物性値-式を検討しているので,なかなか変える事ができません。人間の脳はAIと違ってすぐに切り替わるものではありませんので。
様々な物性値の感温性
液体の様々な熱力学的物性値は、温度に対する関数として得られます。蒸発潜熱、蒸気圧だけでなく、密度、表面張力、粘度、熱伝導率や比熱なども温度の関数となります。こうした物性値の感温性についても考えてみましょう。様々な化合物の表面張力は20℃(もしくは25℃)の値が代表値としてデータ集に記載されています。そして、例えば、水の表面張力は20℃で72.74(mN/m)で、n-ヘプタンの表面張力は20℃で20.86(mN/m)と記載されています。水は極性溶媒で、非極性溶媒のn-ヘプタンは表面張力が低いという言い方をよくします。しかし、蒸気圧曲線の所で述べましたように、極性溶媒にとっての20℃は十分な運動エネルギーを得られない寒い環境で、非極性溶媒のn-ヘプタンにとって20℃は十分運動できる暖かい環境であるという事を忘れてはいけません。南国育ちの人が、寒いシベリアでは十分に運動できないようなものです。ちなみに北方系の人間は鼻が高く、南方系の人間は鼻が低いのは鼻が熱交換器の役割を果たしているからだという説があります。つまり、冷たい空気を暖めてから肺に入れる為に進化の過程で鼻が高くなったのだと。「キリンが高いところにある葉っぱを食べる為に首が長くなった」に匹敵するような俗説ですが、何となくサイエンスぽいのと事実としてそのような傾向があることから、「こんな事を知っている自分は鼻が高い」と語り継がれてきたのではないでしょうか。
表面張力の感温性
表面張力は温度の上昇とともに値が小さくなり、臨界温度(Tc)に近づくにつれ値がゼロになる物性値です(図7)。例えば20℃での表面張力を比べると、アミド>アルコール=スルフィド>炭化水素=アミン>エーテルの順に大きくなります。大まかには極性の順になっていますが、硫黄の入ったスルフィドがアルコールと同じ表面張力なのは受け入れがたいデータではないでしょうか?これは元素の周期律表の第2周期以降の原子では一般的な事ですが、原子核に含まれるプラスに荷電された陽子がK殻、L殻の電子によってシールドされ、M殻以降の電子が分極を起こす事によって引き起こされると考えられています。同じ理由で,臭素,ヨウ素などが入った化合物は表面張力が高いという特徴があります。そこで,表面張力が高い事を極性溶媒の指標にするのは間違っています。ちなみにスルフィド化合物は、蒸発潜熱を沸点で割った蒸発のエントロピーは87.0 J/(mol・K)となりますので、立派な正則溶液であるといえます。
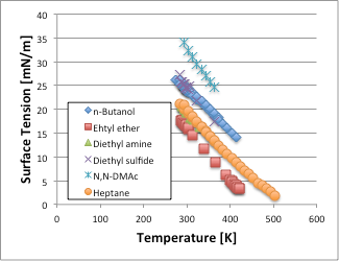
図7. 有機化合物の表面張力–温度依存性
それでは、この表面張力を、換算温度Antoine B / (Tref[℃] + Antoine C)に対してプロットしてみましょう(図8)。換算温度が4以下(温度としては高い)では、有機化合物の種類にはよらずに換算温度が決まれば表面張力が決まります。換算温度が同じという事は、液相から飛び出る分子の運動エネルギーが同じという(同じ圧力を与える)条件下では、表面張力も同じになるという事を示しています。ところが、換算温度が4以上になると2本の曲線に分かれていきます。ヘプタンとブタノールは同じ換算温度で表面張力が低いグループになり、それ以外の化合物は換算温度に対して同一の表面張力を与えるグループに所属します。
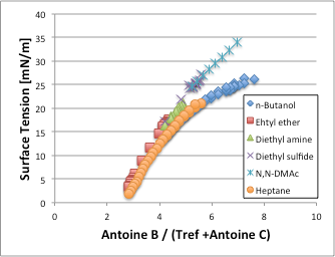
図8. 表面張力–換算温度依存性
ブタノールの挙動に関しては界面活性剤がアルキル基の疎水場相互作用によってミセルを作る事を考えると理解しやすいと思います。ブタノールはある換算温度以下(温度は高い)ではランダムに存在していますが、温度が下がってくるにつれ、アルキル基を液滴の外側に向け(空気層の方が疎水性が高い為)、アルコール基を液滴の内側に向けて配向し始めます。液滴の外からみると、液滴の表面にはアルキル基のみが見えるのはヘプタンと同じであるのでヘプタンとブタノールが同じグループに属してしまうのです。分子の形状や配向力を検討するには表面張力は最適な物性値であると言えます。
沸騰現象で言えば、最初の沸騰核の生成と粗面の関係、泡の大きさなどを決める大事な指標ですし、インクジェットプリンターのノズルから沸騰によって飛び出す液滴の径も、ノズル径と表面張力で決まります。
また、マランゴニ対流という非常に興味深い対流も表面張力の差によって引き起こされます。身近な例では、ワインをグラスに注いだときにワインとグラスの接触した所で見られる、「ワインの涙」がマランゴニ対流によるものです。グラスの端でエタノールが蒸発し、水分比率が高くなると表面張力が高くなり、対流が起き、涙のようなものが形成されます。水が蒸発しただけでも温度が下がり表面張力が下がるので対流が起こるので、例えばコーヒーを垂らし乾燥させると、コーヒーの粉がその対流に乗って液滴の端に集まる、コーヒーステインという模様を作ります。密度差対流と区別する為に、重力の無い宇宙空間での測定が、ISSの「きぼう」で行われているのでご存知の方も多いかもしれません。沸点、表面張力の異なる混合溶媒を蒸発させる時には考慮に入れる必要があるかも知れません。
粘度の感温性
次に液体の粘度を見てみましょう。粘度も表面張力と同じで温度が上昇していくと、値が小さくなる物性値です(図9)。ただし、表面張力と異なり、温度が臨界温度に達しても値はゼロにはなりません。この粘度を、換算温度Antoine B/(Tref[℃]+Antoine C)に対してプロットしてみましょう(図10)。するとアルコール以外はきれいに1本の直線に乗る事がわかります。つまり、換算温度が同じであれば、分子の運動エネルギーも同じになり、その時の粘度も同じになるということです。換算温度に対する感温性も化合物によって違いはありません。唯一異なる挙動を取るアルコールは、同じ換算温度では粘度が非常に高くなります。これは強い水素結合によって見かけ上の分子体積が大きくなるためです。こうした粘度の換算温度依存性を調べる事によって、水素結合が3次元性なのか、2次元性なのか、ダイマー性なのかを知る事ができるので非常に重宝する指標となります。
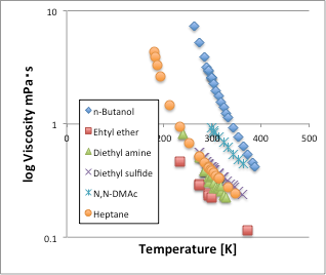
図9. 有機化合物の粘度-温度依存性
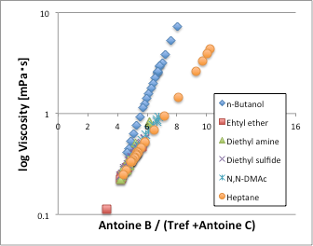
図10. 粘度–換算温度依存性
粘度は,流れの乱流度を表す,レイノルズ数を決める重要な物性値です。このレイノルズ数については次章に譲るとして,別の観点から粘度と蒸発を見てみましょう。塗料は,顔料,ポリマーそして溶媒の組み合わせで作られています。塗料を塗る際の大事な特性として,液だれをしないというのがあります。これは垂直な壁に塗料を塗った時に重力で塗料が下の方に垂れてきてしまう現象です。これを防ぐには,塗料の粘度を高くすればいいのですが,すると今度は,薄く塗れない,塗った時にハケの筋が残るという問題が生じます。そこで,塗料の設計では,せん断をかけた時(刷毛でかき混ぜている時)はサラサラしていて,静止した時には粘度が上昇して固化するチキソ性をうまく活用します。チクソトロピーとはゲルのような塑性固体と,ゾルのような非ニュートン液体の中間的な物質が示す性質です。そして,塗装が終わった段階で,粘度が低く沸点も低い貧溶媒が先に蒸発し,系の粘度がさらに高くなり,ポリマーをよく溶解する高沸点溶媒がゆっくり蒸発することによって液だれせず,表面が緻密なポリマー層に覆われた塗膜が形成されます。複数のポリマーを使う場合には,蒸発をコントロールすることによって,ポリマーの組成が表面から傾斜する機能性塗膜を形成する事ができます。
密度の感温性
液体の密度とはどのような物性値でしょうか? 通常は容積が一定のメスフラスコなどに液体を入れ、その重さを測定して密度を得ます。分子論的に言えば、分子量を分子体積で割った値が密度になります。多くの場合、液体は温度が高くなると密度が小さくなります。すなわち、温度が高くなると、分子体積が大きくなります。分子体積が大きくなるというのはどういう事でしょうか? 炭素—炭素の結合や炭素-水素の結合が長くなって、分子が巨大化する? そんな事はありません。分子の運動が激しくなって、分子同士の衝突が多くなり、平均的な分子間距離が長くなるため見かけ上の分子体積が大きくなります。空気との衝突を避けるため完全な真空状態に1molの液体を入れれば、気体になると1モルの液体は0℃で約22.4リットルになって1気圧の圧力になります。液体には圧力をかけても体積はほとんど変わらない為,水の液体は0℃,1気圧まで加圧しても約18mlですが、同じ0℃,1気圧でも気体なら22.4リットルになります。
逆に,室温で気体の化合物を液体窒素で冷却して液化させることを考えましょう。容器をまず真空に引き,液体窒素につけます。バルブを開いてガスを導入して容器を液体で満たします。容器に入った化合物の質量はわかりますし,容器の容積もわかるので液体窒素の温度での密度は計算できます。そしてバルブを閉じて室温に戻した時に容積も中に入っている質量も変わらないので,液体窒素の温度でも室温でも密度は変わらないことになります。
これが、密度が関わる物性値の感温性を理解する事が難しくなる原因です。
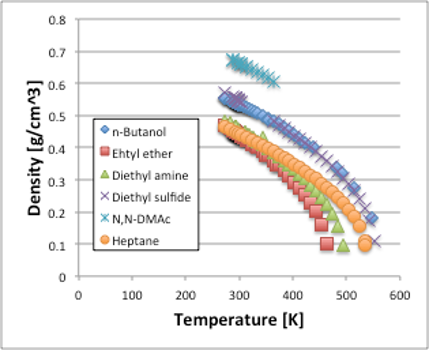
図11. 密度の温度依存性
実際の液体を例に、密度の温度依存性を見てみましょう(図11)。温度が高くなるにつれ、密度が低下していくのがおわかりいただけると思います。化合物の傾向としてはアミド化合物が一番密度が高く、アルコールとスルフィド化合物がそれに続き、炭化水素、アミン、エーテルと表面張力と同じ傾向になります。アルコールとスルフィド化合物の曲線がほぼ一致するのも表面張力の場合と同じです。事実,表面張力の推算式の中には,Macleod-Sugden法というパラコールと液体,気体の密度を結びつけた式があるくらいで,傾向が似てくるのは当たり前とも言えます。表面張力との違いは,温度が高くなるにつれ,密度は急に小さくなることです。そして表面張力は臨界温度ではゼロになりますが,密度の場合は臨界密度(MW/臨界体積)になり,ゼロにはならないことです。そこで,Macleod-Sugden法では表面張力の感温性は(特に温度の高い領域では)正しく評価できません。
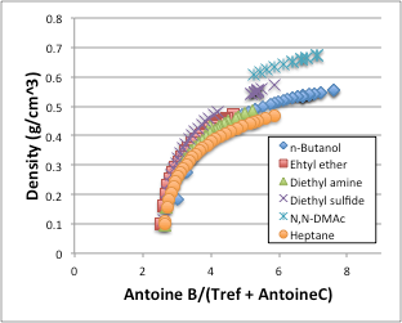
図12. 密度と換算温度の関係
蒸気圧を一定にする換算温度を利用しても,密度の感温性が化合物ごとに異なってしまう事は図12からも明らかでしょう。この事については,次章で臨界点からも考察してみましょう。
沸騰現象の中で敢えて密度の感温性を取り上げているのは、密度差による対流が重要だからです。地球の温暖化で北極の氷が溶けているのはご存知でしょう。またハリケーンや台風が年々強烈化しているのも実感として認識しているのでは無いでしょうか? 黒潮の蛇行なども含めて異常現象の大元は北極の氷が溶けた事であるという理論があります。海の水は電解質が溶けているので融点降下で0℃では凍りませが、北極での気温では海水は凍ります。水が凍ったときには塩分は含まれませんので、氷の下の海水は塩分濃度が高くなります。そして海表面に近いほど強く冷却されます。そこで、塩分濃度が高く冷たい海水は比重が重くなり沈んで行きます。これが北極を起点とした深層海流になります。大西洋を通り、太平洋の北に達すころ海表面に出てきて暖められた暖流となって戻っていきます。およそ2000年かけて地球を一周すると言われています。最近はこれをくみ上げてペットボトルに入れて売っているので聞いた事があるでしょう。「地球規模の熱循環の起点は北極の濃い塩分濃度の海水が沈み込むことにある」とすると、北極の氷が溶けるという事は何を意味するでしょうか? 薄い塩分濃度の海水は比重が軽く、沈み込む力が弱くなるという事です。薄い塩分濃度の海水は、翌年の冬には、融点降下が少なくなるので凍りやすくなり、見かけ上の氷の面積の減少は小さくなりますが、文字通り、水面下で起こっている事は深層海流の流れが弱まる事を意味しています。するとそれにつれて赤道付近の熱は行き場がなくなり、蒸発潜熱を奪って気化して、暖かい空気は比重が軽くなって上昇気流になり、台風やハリケーンの形で熱を北に循環させる事になります。水が運ぶ熱量と空気が運ぶ熱量は桁違いですから、強烈に頻繁に起きるようになる。これはあくまでも一つの解釈で真実ではないかもしれませんが、「液体、気体の比重差」による熱循環は沸騰の際の泡の浮力にも関わってくる大事な概念なので敢えてここで紹介させていただきます。
ちなみに、富山沖の深層海流は水深800mぐらいです。マッコウクジラが潜る深さは最大3000メートルですので、余裕で深層の水を飲む事ができますが、不思議に思った事は無いでしょうか? 魚は体内に浮き袋を持っているので、浮き沈みは浮き袋の大きさで調整できます。クジラはほ乳類なので浮き袋を持っていません。どうやって浮力を調整しているのでしょうか? 実は、マッコウクジラの頭には脳油器官という特殊な器官があって、そこにワックス状の脳油が詰まっています。そこに海水を流して冷やすと固体の状態に近づくため比重が高くなり沈んでいきます。浮上したいときには、血流(ほ乳類なので血液は暖かい)を流して比重を下げるのです。意思の力で比重を変えられるとは、すごい生物ですね。自分も体重計に乗るときに「意思の力で」、と思っても残念ながらいくら空気に体する比重を変えても体重は変えられません。。。
相対蒸発速度(RER)
塗料やインクの分野では、顔料(染料)、ポリマーと溶剤を使って美しいコーティングを行います。最近は環境を守る観点から水系のエマルジョン塗料も多くなってきていますが、耐久性の観点から、まだまだ溶剤系の塗料が多く使われます。ただ、例えばアメリカでは発行部数が1500部以上の新聞のうち95%が大豆油を使ったインクを使っています。新聞紙は家庭内にあり、子供やペットが舐めたりする、揚げ物の油を吸わせるなどに使われる事があるためとされていますが、日本ではどうなのでしょうか?
大豆油は、リノール酸(約50%)、オレイン酸(20%強)、パルミチン酸(約10%)、リノレン酸(約10%)、ステアリン酸(約5%)の脂肪酸混合物で、分子量が大きく蒸発しにくい溶媒です。インクを紙や木材に塗るときには、溶剤は紙の繊維などに吸収されていくのでそれでも乾いていきますが、金属やプラスティックの塗装には高沸点溶媒は使えません。こうした塗料やインクなどに使われる毒性の低い、いわゆる環境に優しい(オゾン層破壊、地球温暖化)溶媒は、多くの場合、相対蒸発速度(RER: Relative Evaporation Rate)の値が付記されています。液体の蒸発速度は単位時間、単位面積あたりの蒸発重量で測定し、通常25℃における酢酸ブチルの蒸発速度との比で表します。
液体を蒸発させるときには、液体の上の空間が閉じられていれば、飽和蒸気圧分だけ蒸発した後に、見かけ上、蒸発は止まります(液相から気相へ蒸発する速度と、気相から液相に戻る速度が同じ、平衡状態に達する)。オープンな環境で試験したとしても風速(飽和蒸気圧分の気体分子を流し去る)などの影響を受けて試験結果が大きく変わる事があります。
寒中水泳や熱いお風呂に入る時の事を考えてみましょう。入ってじっとしていればすぐに体表面に接する水は体温近くになりますが、水を撹拌したらとてもじゃないですが入っていられません。銭湯で子供が湯船に飛び込んだりするのは迷惑な話です。そこで、スキューバー・ダイビングでは熱伝導性の悪いゴムのスーツに水を入れたウエットスーツを使います。撹拌されても体表面の水の層がはがれないようにする為です。また、液体は蒸発する際に蒸発潜熱を奪うので、液体の温度は低下し、蒸気圧も低くなってしまいます。冬場の寒い時期に風が吹くと温度以上に寒く感じるのは、暖まった体表の空気が飛ばされる直接皮膚が冷却されるだけでは無く、皮膚から水分が蒸発し蒸発潜熱を奪う事にも起因しています。みぞれまじりの雨で衣服が濡れて強い風が吹いたら最悪です。
皮膚から水分が蒸発した結果、乾燥肌になるので、水の蒸発を押さえる為にワセリンを塗ります。ちなみに、冬場に食べごろを迎えるつるつる光った赤いリンゴ。このリンゴの表面のワックスは果物が乾かないように自然に分泌されるものです。見かけがよくなるので、人工的なワックスを塗ったリンゴも市場に出回っていますが。。。
話をもとに戻しましょう。蒸発速度です。蒸発に関する熱力学的な物性値のプレーヤーを確認しておきましょう。
ある基材の上に基材と同じ(25℃)温度の液体を垂らします。そこに一定の温度、湿度の一定速の気流を流します。液体は25℃の温度に相当する飽和蒸気圧分蒸発します。すると液体は蒸発した分、蒸発潜熱を奪われ温度が下がります。基材の熱容量が十分大きければ、基材の温度は変わらないので基材から液体に向かって熱が移動します。(フーリエの法則)その熱の移動のしやすさは液体の熱伝導率で決まります。液体表面の冷えた液体が内部と入れ替わるのには表面張力や粘度が影響するでしょう。ある熱量が与えられたときに(蒸発潜熱を奪われたときに)どれだけ温度が上がるか(下がるか)を決めるのは比熱です。また、蒸発速度は重量の減少速度なので、液体の分子量も必要になるかもしれません。
相対蒸発速度(RER)と熱力学的なプレーヤーの物性値が十分にある液体109種類について考察してみましょう。まず、すぐに思いつくのが,「沸点が低いものは蒸発しやすい」。確かにその傾向はあるので、確認してみましょう。図13に示すように傾向としては正しいのですが十分な精度とは言えません。
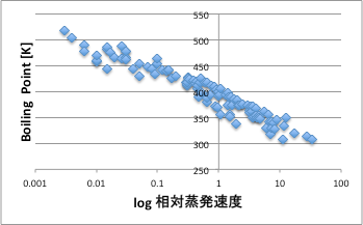
図13 log RERと沸点の関係
どこで間違ったのかというと、沸点の蒸気圧は760mmHgでどの液体も同じなのですが、沸点と測定温度の25℃の間隔は液体によって異なる事です。そして、25℃から沸点までの蒸気圧曲線も液体によって特有の曲線になるので、RERを沸点から予測するのは困難である事がわかります。
そこで、各液体のAntoine定数から25℃での蒸気圧を計算し、RERに対してプロットしてみます(図14)。
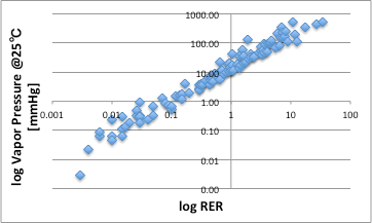
図14 log RERと25℃における蒸気圧の関係
大まかには良いのですが、一部の液体で、蒸気圧が高いのにRERが低い(直線で上ぶれ)している液体があります。蒸気圧が高いのに蒸発速度が遅いのは、蒸発潜熱を奪って液体が冷却されているからでは無いかと考え蒸発潜熱(J/g)に対してプロットしてみます。
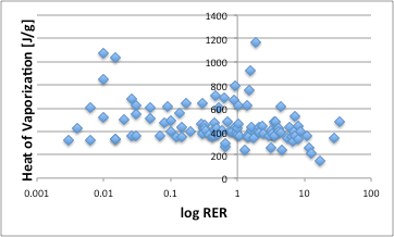
図15. log RERと25℃における蒸発潜熱(J/g)の関係
ところが、相対蒸発速度と蒸発潜熱(J/g)には全く相関が無い事がわかります(図15)。どこで間違ったのかというと、蒸発潜熱の単位です。蒸発速度は重量減少の速度なので、蒸発潜熱をJ/gで考えたのですが、実は図16に示しますように相対蒸発速度は蒸発潜熱のJ/molと高い相関があります。
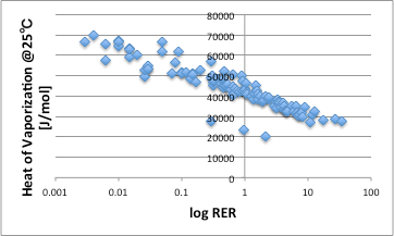
図16. log RERと25℃における蒸発潜熱(J/mol)の関係
線から大きく外れる3点は、分子量の小さいカルボン酸化合物で、分子間水素結合でダイマーを作り、気相中でもダイマーを形成しているのでこのような結果になります。
Antoineの蒸気圧式で、Antoine B定数は蒸発潜熱(KJ/mol)と相関がある事を示しました。従って、RERが蒸気圧と高い相関があるという事は、とりもなおさず、RERはモル単位の蒸発潜熱と高い相関がある事は自明の事だった訳です。ただし,Antoineの蒸気圧式で使っている蒸発潜熱は沸点における蒸発潜熱です。25℃における蒸発潜熱は,沸点の蒸発潜熱に25℃から沸点までの温度差に液体のモル比熱をかけた熱量を足せば良いので、比熱の単位もモルで扱わなければなりません。RERに対してモル比熱をプロットすると、図17のような相関が得られ、液体を暖めるのにより多くの熱量が必要な液体は蒸発させにくい傾向があることがわかります。
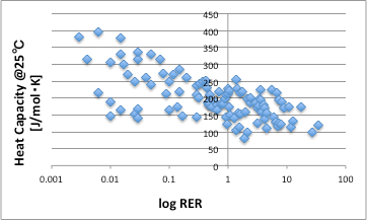
図17. log RERと25℃におけるモル比熱の関係
この比熱の単位をJ/g・Kで取ってしまうと、多くの液体で比熱は、図18に示すように、おおよそ2ぐらいになり、比熱は蒸発速度には影響しないと解釈が異なってしまいます。
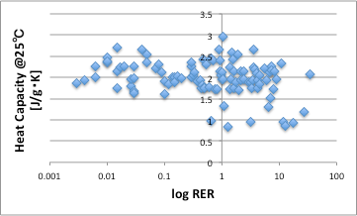
図18. log RERと25℃における重量単位の比熱の関係
蒸発がグラムでは無くモルに支配されているという意味では、Antoineの蒸気圧式では、モル蒸発潜熱、モル比熱の効果は既に組み込まれているので、図14で直線より上ぶれする液体の説明にはなりません。グラフには示しませんが、表面張力が高い液体は蒸発しにくい、粘度が高い液体は蒸発しにくい傾向はありますが、同じように上ぶれする液体の説明にはなりません。
熱伝導率はどうかというと、これも重量比熱と同様で、ほぼすべての液体で、150mW/mK程度となり、蒸発速度とは相関がありません。熱伝導率は、単位面積、単位厚み当たりの係数なので、次元的には体積になり、モル単位で効いている蒸発とは相関が低くなります。
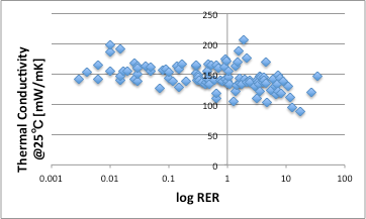
図19. log RERと25℃における熱伝導率の関係
図14で直線より上ぶれする液体の説明できるプレーヤーは居なくなってしまいました。
そこで思い出して頂きたいのですが、25℃、1気圧という測定条件の意味です。これは地球基準の値であって分子の基準点では無いという事です。そこで、RERに対して換算温度Antoine B/(25[℃]+Antoine C)をプロットしてみましょう。
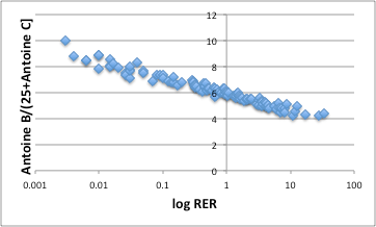
図20. log RERと25℃の換算温度
図に示すように、非常にきれいな相関が得られます。25℃での蒸気圧をプロットした図14は縦軸がlogプロットであった事を考えると著しい精度の向上がはかられた事になります。
この事は、地球基準の25℃、1気圧で考えていても蒸発速度はわからないけど、T1mmHg、1mmHgという分子基準で考えれば、どんな液体でも蒸発速度は同じである事を示しています。
ここで、読者にお願いしたい事があります。
ここまでモルで考えてきて、はっきり解釈できた蒸発現象であるのに、何故蒸発速度自体は重量の減少速度なのか?という問題です。筆者の力量ではどうしてもその部分の説明がつきません。新しい解釈をもとに、研究を押し進めてくれる若手研究員が続いてくれる事を願ってやみません。
それでは、もう一つの分子基準を考えてみましょう。分子の状態を考えたときに3つの基準点が考えられます。一つは分子が運動を全くしない絶対0度。これは宇宙基準ともいえます。次に3重点。これは測定や推算が難しいので、T1mmHg、1mmHgを代用しています。最後は臨界点。臨界点では臨界温度(Tc)、臨界圧力(Pc)と分子間力がちょうど釣り合って、液体でもない、気体でもない分子状態になりますので、古くから分子の基準点として利用されてきました。そこで、25℃の蒸気圧が臨界圧力からどれだけ離れているかを示す還元圧力を相対蒸発速度に対してプロットしてみましょう。
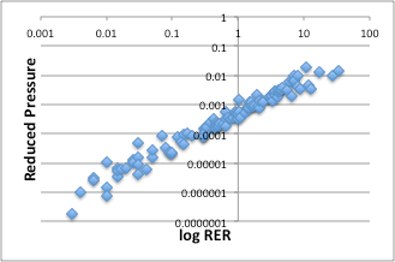
図21. log RERと還元圧力の関係
予想されたように、基準点を(T1mmHg、1mmHg)から、(Tc、Pc)に変更しても、同じようにRERが説明できる事がわかります(図21)。
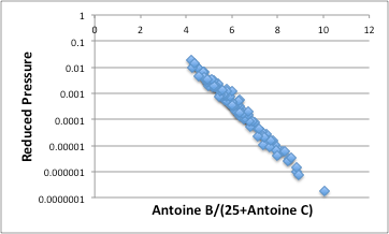
図22. 換算温度と還元圧力の関係
そして、図22から換算温度と還元圧力については非常にきれいな関係がある事が確認できます。
蒸発現象はどちらの基準点を使っても大差はありませんが、低温の液体を考えるなら、(T1mmHg、1mmHg)を使い、気体を考えるなら、(Tc、Pc)を使うのが合理的では無いかと私は思っています。
何故、化学工学や伝熱工学では物性値の単位をモル・ベースでは無く、重量ベースで考えてきたのでしょうか? それは考え方の基本が水ベースだったからです。水は高々分子量が18で窒素分子の28よりも小さいのに、沸点は100℃です。蒸発潜熱を沸点で割った値は109ですので正則溶液からも外れるのは他のアルコール化合物と同じですが、重量ベースの蒸発潜熱は2444J/gとアルコールなどと比べても倍の値になります。熱伝導率は25℃で607mW/mKと今回検討した液体の3倍近い値になります。モル比熱は75.358 J/mol・Kなので小さめの値になりますが、分子量が小さい分、重量比熱は4.187 J/g・Kと通常の液体の倍近い値になります。その割に粘度は低く0.89mPa・sと通常の溶媒並みです。このような不思議な液体をベースに拡張をしてきたので、不思議さが際立つ重量ベースで考えてきたのでしょう。伝熱の分野では熱伝導率は重要なファクターになります。この物性値はモル・ベースではありません。単位面積、単位厚み当たりの係数になるので、それに密度が加われば重量ベースになります。そこで、比熱なども重量ベース、蒸発潜熱も重量ベースで理論が組まれて行ったのでしょう。熱と仕事を考える上でも重量ベースで考える方が有利です。蒸発というモル・ベースの事象が絡まなければ、それはそれで合理的です。しかし蒸発が絡んでくると、水の不思議さから外れれば外れるほど(水素結合性の少ない液体ほど)理論が合わなくなって行く事が予想されます。Antoine定数のところでも触れましたが、非線形の式は解が複数存在する可能性があります。本来蒸発に関係する比熱の単位をJ/g・Kにとり相関がなくなったぶん、比熱の係数を下げ、それを補う形で、他の物性値の係数を高くして全体を調整し精度の高い式を構築する事は可能です。ただし、データ数が少ない場合は。しかし、その係数の値を信じて分子設計をすると、とんでもない結果になり、また係数を微調整する、を繰り返す事になります。今回のように100系を超えるデータがあった場合には、おそらく普通の統計解析ソフトでは解析不能になるでしょう。
ちなみに,分子基準の(T1mmHg、1mmHg)や(Tc、Pc)を使っても、水のRER=0.4は線の上に完全に乗ります。いわゆる筋の良い解釈をすることは,囲碁や将棋のように多くの解が存在する問題を解く上で非常に有利になります。
ここまでは、液体の物性の話でした。大気圧の下、有機化合物が標準沸点に達しても沸騰は起きません。液相から飛び出す分子と、気相から戻る分子が平衡に達し、その温度での分子の運動エネルギーが壁に衝突して観測される圧力が大気圧に等しくなっただけです。沸騰とは液相中に蒸気の泡ができ、それが成長していく現象なのでこれまでの液体中心の考え方では理解が進みません。分子の基準点としては(T1mmHg、1mmHg)と(Tc、Pc)のちょうど中間の領域の話になると思うので、次章では臨界点基準の熱物性を考えてみましょう。
化学工学はITに見捨てられた分野とかいう自虐的な言い方がありました。流れの解析用のソフトなどはずいぶん進歩しましたが,昔からある有限要素法が,高速化,大容量化したのでメッシュが細かくなっただけなので,ITの進歩という感じはあまりしません。何故ITに見捨てられたのかと言えば上記のような難しい問題が内在していたからです。最新のAIならどうなるでしょうか? 自動的にモル・ベースを重量ベースに変えて式を組み立てて行くくらいのAIが出現するのはそう遠く無い事でしょう。Antoine BをKJ/Kgベースに変えて,空間の圧力ではなく,空間中の重量を予測する3パラメータを決定する式ぐらい簡単に作るかもしれません。筆者は、かれこれ20年間ニューラルネットワークを使った物性研究をやってきて得られた結論は、精度が高い,中がブラックボックスのニューラルネットワークより、中身が見える精度の低いニューラルネットワークの方が大事というものでした。その発想で定めたAntoine定数が蒸発現象の解釈に,たまたま役に立ったということです。これは既に過去の話で,現在は,次の時代に向けてAIをどう教育したら自律的に化学-化学工学-式の組み立て-逆設計をこなしていかれるのかに焦点は移っていています。そうした時代に若手研究者の卵が何を学び社会へ巣立っていくべきか,学生と考える機会を提供いただいている横浜国大には感謝しております。
