2018.12.29
情報化学+教育 > 情報化学 > PLS(Partial Least Squares)法
PLS(Partial Least Squares)法は計量経済学者であったHerman WoldとSvante Woldによって開発された新しいモデリングの方法です。
主成分分析と似ていますが、プログラム的には大きく異なっています。
特に化合物のスペクトル・データのように説明変数が膨大になる時や説明変数間に相関がある(共線性)場合に効果を発揮します。
最近のMaterials Informaticsなどでは、RDKitなどを用いて膨大な化合物情報が得られるようになりました。./RDKit.html
例えば「化合物の水への溶解度を推算するのに、1000を超える化合物情報(FP: Finger Print 指紋)を用いて機械学習を行って予測を行う」などが行われています。
そうしたモデリングを行う際に、PLS回帰法やニューラルネットワーク法が使われています。
PLS法自体は統計解析パッケージに搭載されていますし、Pythonなどで簡単に試してみることができますが、如何せん情報が非常に限られていて手軽に試せるような状況では無いように思えます。
(情報が限られているという意味は、例えば統計解析用の書籍には主成分分析がほとんどでPLSは余り記載が無い。Webでは情報がありすぎて具体的にどう良いかが見えてこない。)
ブラウザー上でPLSを計算するプログラムを作ったので、それを元にPLS法の使い方を学んでみましょう。
プログラムのタネ本は、「Excel VBAによる化学プログラミング、佐藤寿邦・佐藤洋子共著 培風館 2002年」です。
ここに記載のVBのプログラムをJavaScriptに変換しました。
慣れてきたら次の書籍で深く学べば良いでしょう。
- ケモメトリックス 化学パターン認識と多蛮量解析 宮下芳勝・佐々木慎一著 共立出版 平成6年
- 化学者のための多変量解析 ケモメトリクス入門 尾崎幸洋・字国明史・赤井俊雄/著 講談社サイエンティフィク 2002年
- ケモインフォマティックス 予測と設計のための化学情報学 J.Gasteiger・T.Engel 編 船津公人 監訳 船津 公人 ・佐藤 寛子 ・増井 秀行 訳 平成17年
線形重回帰、主成分回帰、PLS回帰どれにも共通して言えることは、化合物の物性と分子構造との関係を解析したいということでしょう。
(場合によっては、プロセスと効率など分子では無いものも含まれますが。)
知りたいものを目的変数(y)と呼びます。
知りたいものの性質を表すものを説明変数(x)と呼び、これらは複数あることがあります。
そこで、
y=function(X1・・Xn)
の関係を定量的に知りたい時に回帰計算を行います。
ある目的変数を高くしたい(低くしたい)時に、説明変数をどのように動かしたら良いかを定量的に知りたい時と考えれば良いでしょう。
(それ以外、毒があるない、燃える燃えない、甘い苦いなどを区別するのに定性的に区分するという時にも主成分分析、PLS解析は使われますが、重回帰法という時には定量的な解析を指すと自分は考えています。)
主成分回帰とPLS回帰は比較的似ています。
どちらも、説明変数がスペクトルデータのように膨大であったり、実験データ数よりも説明変数の方が多いケースに使うのは有効です。
説明変数の次元数を下げるとか言います。
もう一つ大事な点は、説明変数間の相関が高い(共線性のある)データが存在する場合、重回帰法では正しいモデリングができませんが、主成分回帰とPLS回帰では正しくモデリングできるなどの違いがあります。
主成分回帰とPLS回帰の違いというのは、(素人である自分には説明が難しいのですが)主成分分析は逆行列を求めなくてはならない手間が大きいです。
行列が大きくなってくるとPLSの方が有利になります。
逆にPLSには無く主成分分析にある特徴は何かあるのでしょうか?
難しい事は説明できませんが、主成分分析なら、エクセルが使える程度で予測値まで計算できる事はメリットかも知れません。
スペクトル解析
習うより慣れろで実際にやってみましょう。
まずはプログラムがきちんと動作しているかの確認のためスペクトルデータの解析を行ってみましょう。
例題は種本に載っていたガソリン類の近赤外スペクトルとオクタン価の関係です。
下記のデータをコピーして表計算ソフトにペーストしておきます。
このデータは、1−36水準の近赤外のスペクトルデータと第2列目にはオクタン価が入ったテーブルになります。
つまり、目的変数はオクタン価、説明変数はスペクトル値となります。
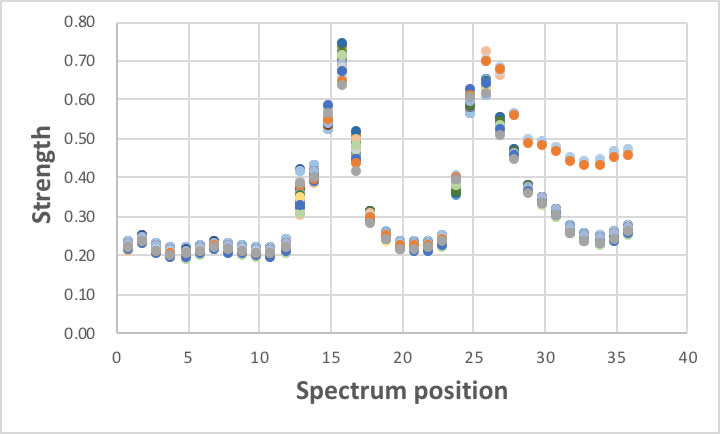
全部で57種類のガソリンの36箇所での吸収強度を図に表すと上記のようになります。
ほとんどのガソリンでスペクトルはほぼ一致するので、図中に57本の線があるようには思えません。
この微妙な差からガソリンのオクタン価を定量的に当てると言うのが最初の例題です。
先ほど取り出したスペクトルデータをPLS計算ソフトの上のテキストエリアにペーストします。

NP値を指定してCalc. PLSボタンを押すとほぼ瞬間に計算結果が下のテキストエリアに表示されます。
この結果を全て選択してコピー、そして適当なテキストエディターに貼り付けておきます。
この出力結果の見方を覚えましょう。
コンピュータのプログラミングに長けているものが見たら直ぐに分かると思いますが、この出力とスペクトル値があればオクタン価を予測するPLS式を簡単に組み立てることができます。
プログラミング作法は別にどこかで説明しましょう。
ここではPLS解析結果のうち大事な項目について詳しく見ていきます。
まず、ここではNP:コンポーネントの数を10と指定しました。
PLSの解析法は、簡単に言えば目的変数Yと説明変数Xの関係を直接求めずに潜在変数を介してモデリングを行います。
最初のモデリングでYの残差がFだったとすると、その残差分をモデリングして徐々に残差を減らしていきます。
その繰り返し計算を何回行うかをNPとして指定します。
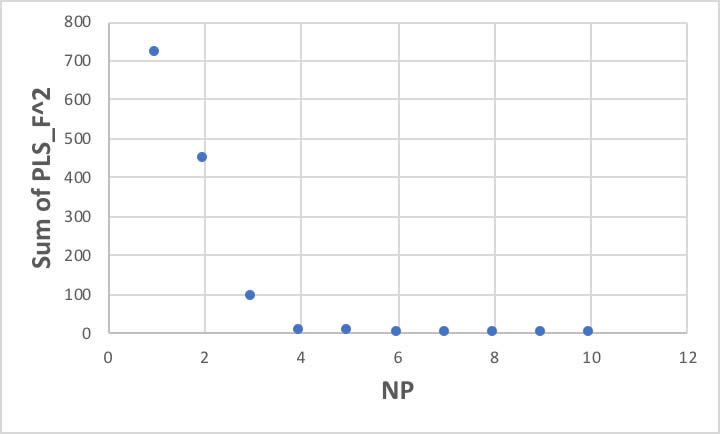
NP値が増えるにつれて、残差項の自乗和は上図のように下がってきます。
NP=4であれば、ほぼ問題ない精度でモデリングできていると考えられます。
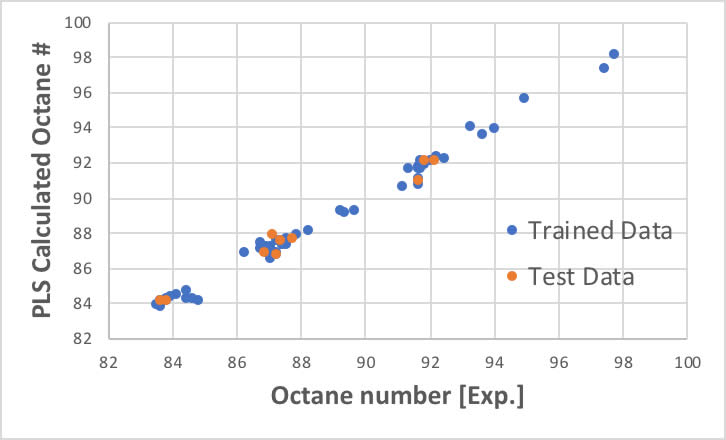
そこで、NP=4で計算した訓練データの比較と、訓練に使わなかったデータの予測性能を検証した結果を上図に示しました。
スペクトルデータだけからオクタン価が予測できると言っても過言ではないことが分かるでしょう。
ただし、Web版では予測機能は搭載していません。必要な情報は吐きだされているので、自分で組んでみましょう。(企業とかで手間を惜しむ場合はPro版を考えてみてください。)
具体的に言えば、PLS_W[i][j]とPLS_P[i][j]、PLS_Q[j]は出力に含まれます。
PLS_Wは荷重行列(Weight Matrix), PLS_Pはローディング、PLS_Qは校正ベクトル(Calibration Vector)と呼ばれます。
後は予測用のスペクトルデータPLS_XP[][]があれば次式でオクタン価予測値(PLS_YP[])が予測データセット数(PLS_MP)だけ求まります。
for(let k=1;k<=PLS_MP;k++){//予測データの数だけループを回る。
for(let j=1;j<=PLS_NP;j++){//ここで、NP回分だけループを回る。
PLS_TP[j]=0.0;
for(let i=1;i<=PLS_PW;i++){
PLS_TP[j]=PLS_TP[j]+PLS_XP[k][i]*PLS_W[i][j];
}
for(let i=1;i<=PLS_PW;i++){
PLS_XP[k][i]=PLS_XP[k][i]-PLS_TP[j]*PLS_P[i][j];
}
PLS_YP[k]=PLS_YP[k]+PLS_TP[j]*PLS_Q[j];//NP回分足し合わされる
}
}この式の意味が理解できれば、自分で作ったPLSの結果を計算するWebアプリを幾つでもHPにおくことができると言うことになります。
石油会社では、高機能性ガソリンとして、ハイ・オクタン価のガソリン販売に力を入れています。
2020年、これが大嘘だと発覚しました。
大元のタンクは共通で、売るときだけ美辞麗句を並べ立て高く販売していました。
ガソリン自体は様々なオクタン価の成分からなる混合物です。
オクタン価とはn-ヘプタンを0、イソオクタン(2,2,4-Trimethylpentane)を100とした時のガソリンの燃焼効率を表す指標です。
基本的には同じ炭素数の化合物なら枝分かれが多いほどオクタン価は高くなります。
直鎖状の炭化水素化合物は水蒸気リフォーミングなどを通じてオクタン価をあげる操作が行われます。
そうしてリフォーミングされたガソリンはどのくらいのオクタン価になったか、どうしたらわかるでしょうか?
そのような時に、少量抜き出して近赤外スペクトルを測定し、目標とするオクタン価に達していたら反応を終了するといったプロセス管理にPLS解析法が使え得ます。
オクタン価自体は分子のトポロジーの問題としても興味深いので別途取り上げます。
このオクタン価の問題をPLSで解いた例は、佐々木先生の「ケモメトリクス」の著書の中にも取り上げられています。
そこでは、43種類の無鉛ガソリンの近赤外スペクトル700点の吸光度をデジタル化して用いているので、PLSならではの例題になっています。(生データは記載されていないので試すことはできませんが)
逆に言うと、今回の例題の36ポイントでの吸光度程度では、PLSの良さを発揮できません。
線形重回帰でも下図のように計算できてしまいます。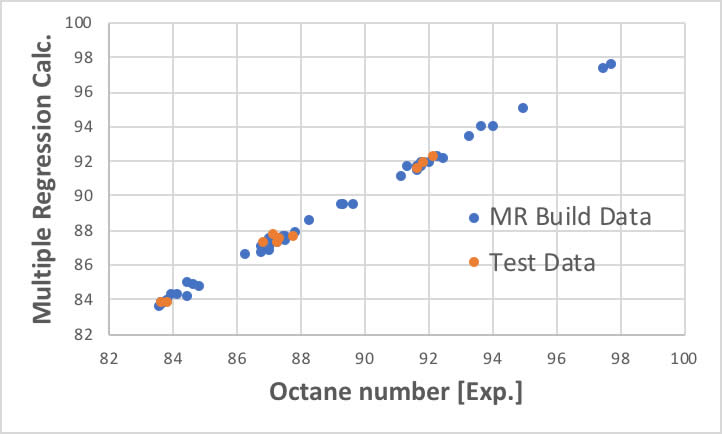
逆にどうすれば、700データポイントから、36データポイントを選び出すことができたのでしょうか?
やり方は記載されていませんが、おそらくGA-PLS(遺伝的アルゴリズムを用いた変数選択PLS)などを用いて、精度を下げることなく、700個から36個を選択したのではないかと思います。
PLS法は本来、共線性のデータがあっても影響を受けにくい解析方法です。
しかし、NPが増えてくると影響を受け出すので、結果に影響を与えない列や共線性のあるデータはなるべく除いてから計算する方が良いのです。
そうしたことを可能にするGA-PLS法は、東京大学の船津先生や、明治大学の金子先生が得意とする解析方法です。
先ほどから共線性と言う言葉が何度か出てきています。
参考図書を読めばちゃんとした定義も含め詳しく説明されていますが、自分にはいまいちピンときません。具体例で計算してしてみましょう。
石鹸製造プロセス
次の例はパソコンデータ分析入門 回帰分析編(技術評論社、小幡卓+堀合啓ー著)にあった例題です。
ある石鹸工場で一月にどれだけスチームを使うか、その時の製造条件などと共に2年分が記録されています。
石鹸というのは油脂を加水分解して脂肪酸とグリセリンに分離します。油脂は温度が低くなると固化してしまうのでスチームで温めなくてはなりません。
気温やら風速など色々なデータが収録されています。
下のデータをコピーして表計算ソフトにペーストしておきましょう。
早速PLSを計算してみましょう。
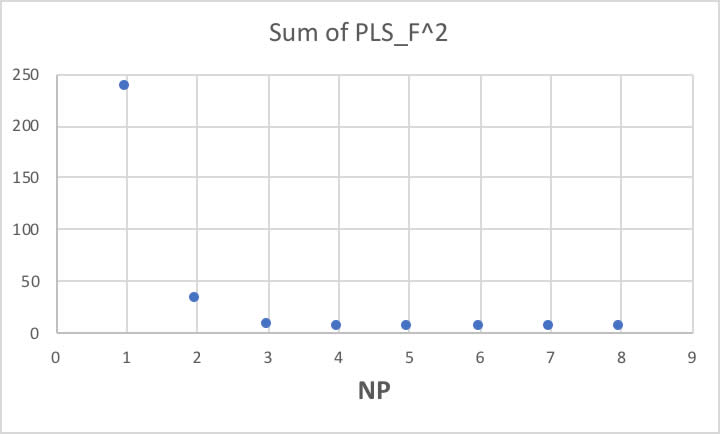
NP=4あたりで精度は一定になるので、NP=4で打ち切ることにします。
その時のモデルは以下のような精度になります。
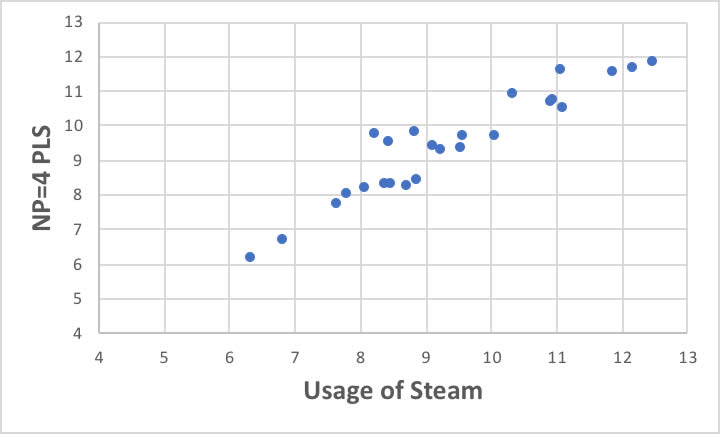
オクタン価の場合と比べてあまり収束性は良くありません。
この問題に対して、与えられた列全てを使って重回帰法で計算をやってみましょう。
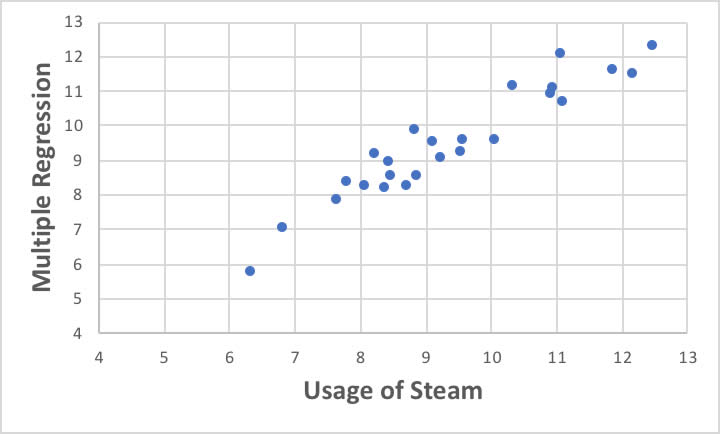
ほぼ似たような精度で、スチームの使用量が計算できます。
それでは、No1の他の条件は同じのまま、風速だけ0.2刻みで増やした時の、PLSと重回帰計算の予測値を比べてみましょう。
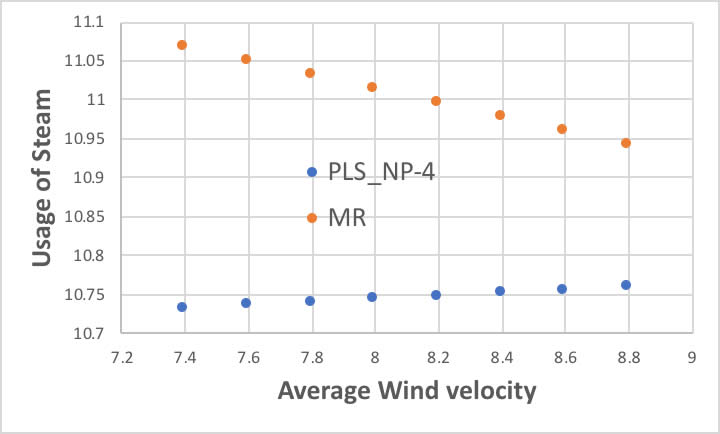
重回帰計算(MR)では風速が早くなるとスチームの使用量は減るのに、PLS回帰ではわずかであるがスチームの使用量は増えると予測します。
どうしてこのような違いが起きるのでしょうか? これが共線性の問題です。
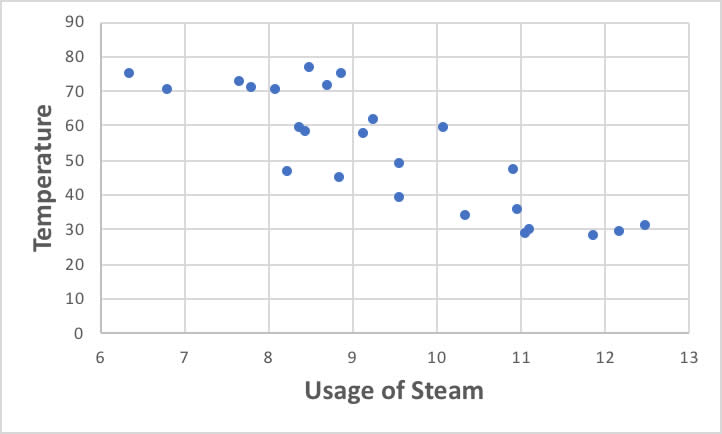
もともと、気温が下がるとスチームの使用量は増えることは上図を見なくても納得できるでしょう。
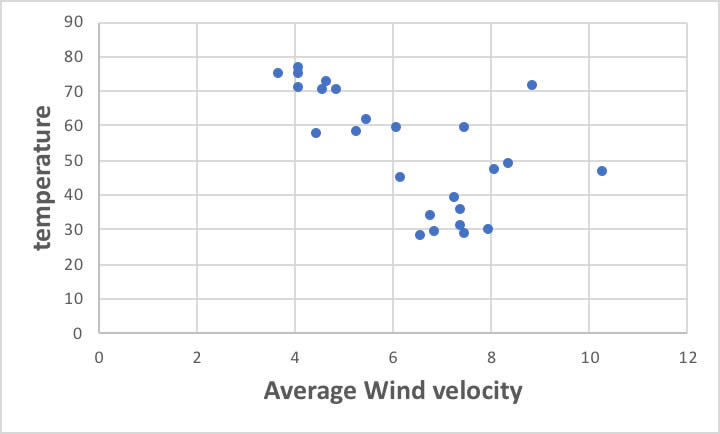
しかし、当たり前の事ながら、冬場は気温が低く風速も早いのです。
このように説明変数間に相関があるような場合を「共線性がある」と言います。
重回帰式の係数は次のようになります。
スチームの使用量=・・・・・・-0.089167839816838*風速
-0.0825515068788824*気温+・・・・+4.38023018565945 風速の係数は符号がマイナスなので風速が早くなるとスチームの使用量はより減ってしまいます。
通常であれば、風速が早い時は(冬場で)気温が低いのです。
気温の重回帰係数もマイナスなので、気温が低いと言うことはマイナス分が小さくなるのでスチームの使用量は増えます。
つまり、風速が早いということと気温が低いということは逆相関であって共線性があります。
そこで重回帰係数は不安定になるので正しくスチーム使用量を予測できなくなります。
脂肪酸量とグセリン量にも正の相関が存在します。
このような問題に対してはPLS法を使った方が解の安定性は高まるとされています。
ただし、この程度の説明変数量であるなら、変数選択重回帰法を取れば良いです。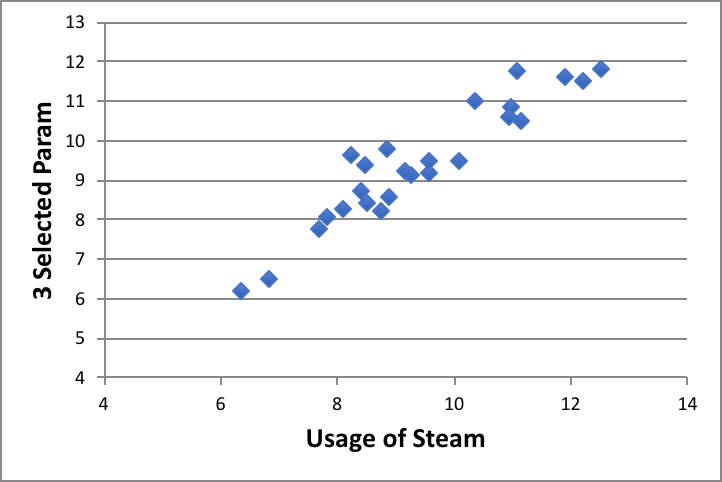
スチームの使用量に対して8説明変数が上げられていましたが、実際には3変数を選択しただけでも上図のように相関が取れてしまいます。
3変数まで減らしてしまえば、風速と気温のような共線性のある項目は選ばれることは少なくなります。
予測式を作る際の多くの間違いは精度を上げすぎるところにあると思います。
NP値を上げすぎる、説明変数を使いすぎる。
見かけは精度が高くなったように見えるかもしれないが、Trainデータに対する記述性が高くなることと、Testデータに対する予測性能が高いこととは別問題です。
PLS法に頼るだけでなく、説明変数の意味をきちんと理解して取捨選択する化学者の能力が大事なのは言うまでもありません。
AIには常識はありません。冬は寒くて風が強い事を教えないのであれば、その分ビッグデータを与えないと正しい答えにたどり着けません。
水への溶解度解析
RDKitとPLS法を用いた成果のうち最も著名なのは化合物の水への溶解度の例でしょう。
RDKitをダウンロードするとTrainとTestのsdf・データが含まれているのですぐに試してみることができます。
Pythonから扱うのであれば、sdfファイルを直接変換すれば良いでしょう。
Pirikaのソフトウエアーを利用するなら、solubility.test.sdfは気をつける必要があります。
このテキストファイルは改行コードが\r\nになっていることと、ファイルの途中でSmiles, SMILESの大文字小文字が混在するので、少し修正しないとSmilesのテーブルは得られません。
しかし、一旦Smilesのテーブルさえできてしまえば、それからRDKitを使って識別子を吐き出させ、PLSで予測式を作成し、以下のような図を作成するのには、5分とかかりません。
2019.1.9:分子結合インデックスの計算に誤りがありました。
本来、Chiパラメータは水素原子は計算に含めないはずです。
Smilesの構造から3次元分子を作る際に水素を付加させていました。
RDKitでは水素の有る無しで計算結果が変わってしまいます。
似たような検討は大学などでも行なっています。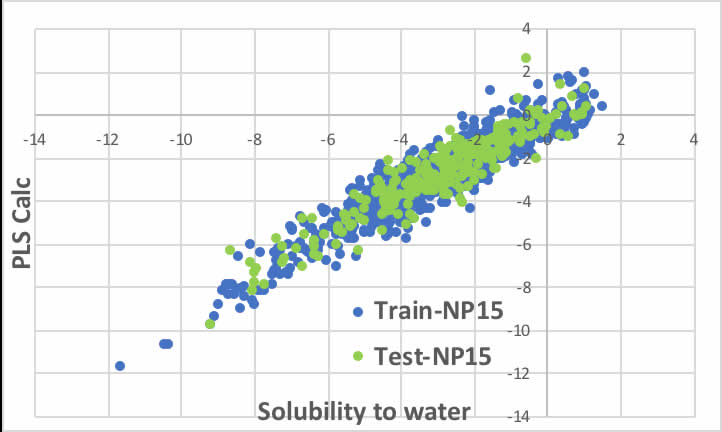
大学での計算例は、RDKitのFP:Finger Printなどを使っているようですが、結果はほとんど違いがないように思えます。
(RDKitの吐き出す識別子はPro版を使っているので117種、PLSの計算もPro版を使っているので予測値も簡単に計算できますが、必要な情報は吐き出されているので、誰でも同じことは検証できるでしょう。企業の研究者など手間を節約したい場合は、Pro版の利用を考えて頂きたいと思います。)
水への溶解度(g/100cc水)のlogをとったものなので、予測値が2違うという事は、100倍溶解度が異なるということで、これを見て十分な精度と言えるかどうかは議論の余地が残るでしょう。
さらにデータ数が増えた時にどうなるか?こちらで解説を行なっています。
こうした例題を通じてさらに深くPLSを使ってみたいのなら、先に上げた参考文献をよく読むことをお勧めします。
PLS法は新しい解析方法なので、どんな問題に適用しても論文化できると間違った風潮があるような気がします。
スペクトル解析など説明変数が非常に多い系を除けば、大抵の問題は、やはり30年前の古い技術、変数選択重回帰法でも解けてしまいます。
変数選択の時に共線性のデータを除外するプログラムなど非常に簡単に書けるでしょう。
SMILESの構造式と水への溶解度のペアがたくさんあったとする。
AIが勝手にRDKitで計算し、分子軌道計算し、自動的に説明変数を集める。
ネット上にある全ての水への溶解度のデータに適合する予測式をPLSや変数選択重回帰法を使ってAIが作成してしまう。
そんな時代は来るのでしょうか?
コンピュータの中で自己対戦を繰り返し、目的とする数式の性能アップを計るのはコンピュータの一番得意とする分野です。
特にPLSを使ったものは自動化しやすいので人間の研究者もうかうかはしていられません。
MAGICIAN養成講座の大事なポイントです。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
