有機化合物の水への溶解度 – http://www.pirika.com/wp/

2021.5.28改定(2013.9.24)

情報化学+教育 > 情報化学 > 水への溶解度を予測するQSPR式の構築法

有機化合物の水への溶解度を計算する方法については物性化学で紹介しました。

ここでは、そうした計算式を構築する時に情報化学をどう駆使していくかを学びましょう。

有機化合物の水への溶解性は、特に医薬品の分野で重要です。

Pirikaでは物性を推算する時に、分子を原子団に分割して、官能基の数、官能基の結合情報から物性を推算することが多いです。この原子団寄与法を用いた水への溶解度の推算式作成法に関してはこちらにまとました。

推算の基本は重回帰法です。
これを有機化合物の水への溶解性を例題に説明しましょう。

まず、この重回帰法を復習しておきましょう。

有機化合物の水への溶解度が分子中の官能基の数で表す事ができるとしましょう。
例えば炭素数が６個の化合物の、水への溶解度の場合、次のようなテーブルを作る事ができます。

水への溶解度が官能基の数(#)だけで決まっているとすると
logS=a*CH3#+b*CH2#+c*CH+d*OH#+e*O#+f*C=O#+g
という式が成り立つと仮定します。

すると

-2.875=a*2+b*4+c*0+d*0+e*0+f*0+g  (1)
-2.746=a*3+b*2+c*1+d*0+e*0+f*0+g  (2)
-0.231=a*1+b*5+c*0+d*1+e*0+f*0+g  (3)
・・・・・・・

という方程式を８つ作る事ができます。

このような式の組み合わせを連立方程式と呼びます。

通常は変数消去法という方法を使って順番に変数を消去します。

例えば式(1)から(２)を引くと、定数のgが消去された新しい式が作成されます（この場合はd, e, fも消去されてしまいます）。

(1)から(3)を引くともう一つa,b,c,d,e,fのみからなる式が作成できます。

その二つの新しい式のfの係数が等しくなるように式の両辺に定数を掛けて式の引き算を行うと係数fを持たない式が一つできます。

このような変数消去法を繰り返すとa,b,c,d,e,f,gが求まります。

変数消去法で変数を求めるには変数の数以上の式が必要になります。

この変数消去法は中学生レベルの解法ですが、高校生で行列と逆行列を習うともう少し簡単になります。（大学の講義で、この話をしたら、「僕たちの世代は”行列”はやっていません」と言われてしまいました。ゆとり世代。。。。）

これらの式を行列で表現すると以下のようになります。

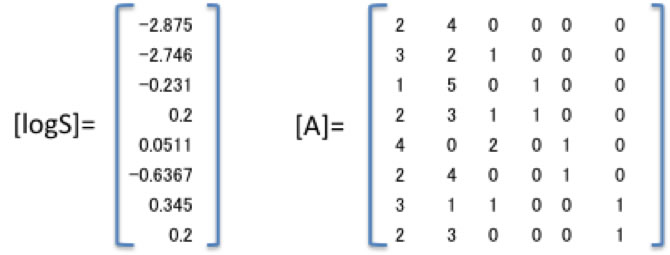
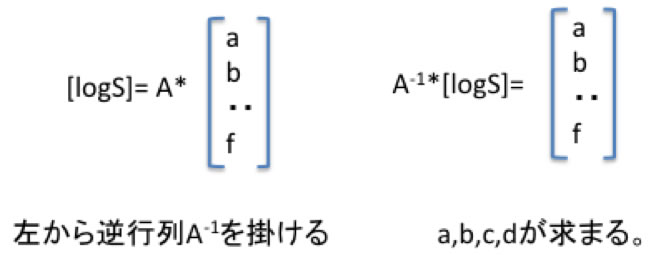
つまり、A行列の逆行列が求まれば簡単にa,b,c,d,e,fが求まります。

逆行列が求まる条件として、m*n行列でm<=nという条件がつくのは変数消去法と同じです。

このa,b,c,d,e,fの事を重回帰係数と呼びます。

こうした重回帰計算はExcelなどにも搭載されているので自分で計算した事もあるかもしれません。
（大学の講義では、PCを持ってくるように言っています。しかし、彼らのExcelに分析ツールが入っていた事は無いので、誰も重回帰計算などやっていないのでしょう。）

実際に係数を求めてみると、

logS=-0.9557*CH3#+-0.3452*CH2#+0.5624*CH#+2.1846*OH#+2.3691*O#+2.7378*C=O#+0.3332

となりました。

この重回帰係数が得られると、例えばOH基、エーテル基、ケトン基は係数がプラスで大きいので、logSを大きくする事が定量的に解ります。

CH3やCH2は水への溶解性をさげる事が定量的に解ります。

課題：ケトンの重回帰係数がアルコールより大きくなる合理的な理由を考えてみましょう。

次に、テーブルに無い化合物について予測してみましょう。

それほど悪くはない予測性能を示す事が解ります。

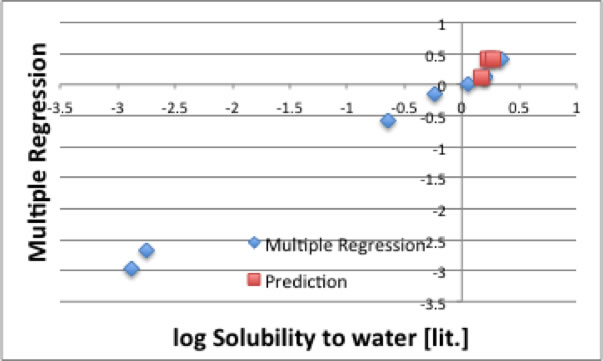
しかし、

同じく炭素数が６で官能基を複数持つものを予測してみると非常におかしな値になる事も解ります。

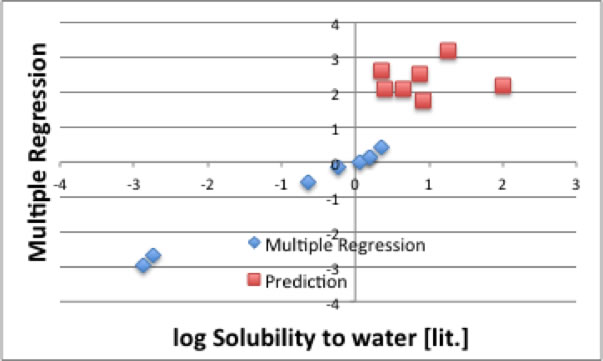
これには２つの原因が混じっています。

最初の問題は外挿性の問題です。

最初に立てた重回帰係数は、
OH基の係数：2.1846、
エーテル基の係数：2.3691、
ケトン基の係数：2.7378
です。

つまり、ケトン基が一番logSを大きくする効果を持っていると計算されました。

ところが、ケトン基を２つ持っている2,5-HexanedioneのlogSは1.253です。
つまり式を立てる時にケトン基の最大数は１であり、ケトン基が2つの時は外挿になってしまうので推算精度が低くなったと考えられます。

この問題に対しては方程式の数を増やすしかありません。

重回帰計算は原子団ごとの相互作用を完全に無視するというのがもう一つの原因です。

式を立てる時にはOH基とエーテル基を両方持つ化合物が入っていません。

これは外挿の問題でもあるので方程式を増やせば外挿ではなくなります。

ところが、データをいくら増やしても、例えば分子中にカルボン酸基とアミノ基を持つ化合物、アミノ酸が特異的な溶解性を持つ事は重回帰法では正しく認識させる事はできません。

平均的なカルボン酸基の重回帰係数と平均的なアミノ基の重回帰係数で計算された答えを返します。

これを回避する為にはHC(NH2)COOH基を定義するしかありません。

このように方程式と官能基を増やしながら溶解性の予測式を作成していきます。

それでは、溶解度のデータがたくさんあればExcelの重回帰計算と合わせれば精度の高い推算式を作成できるでしょうか？

例えば典型的な溶媒600種類を集めたデータベースの化合物の水への溶解度を検討してみました。

データベースには432の溶解度のデータがありました。

そしてそのデータに対して官能基を168種類、分子の形状因子を3種類定義したテーブルを作成します。

このデータに対して重回帰法で官能基に対する重回帰係数を求めてみます。結果は次のようになりました。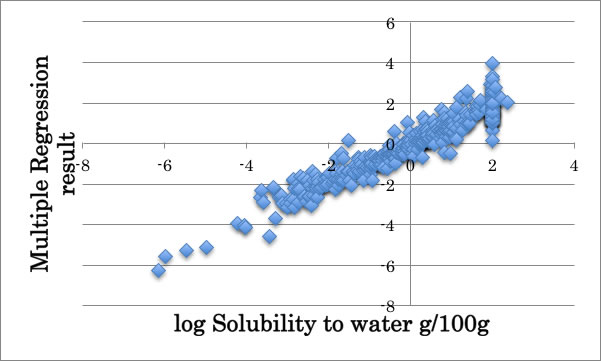

一見して明らかなように、logSが２付近で誤差が非常に大きくなります。

このような結果になる原因は、通常、100％水溶性の化合物は水100ｇに対して∞溶解してしまいますが、データ値としては100ｇの水に対して100ｇ溶解する、つまりlogSは2で実験は打ち切られてしまうからです。

Excelなどの解析ソフトを使ってそのデータを使って解析すると必ずこのような計算結果になってしまいます。

例えば引火点などでも、110℃以上の場合には測定されず、>110℃と表記されているものがあります。

屈折率では、1.2以下などという記載もあります。

データベースの種類にもよりますが、データベース中のカラムには属性を設定しなくてならない事が多く、データがテキストであるのか数値であるかを事前に設定しなくてはなりません。

数値カラムにテキストを入力する事はできないので、>110℃の場合110という数値が一人歩きしている場合が多くあります。

蒸発潜熱の場合、最小値は０です。
従って蒸発潜熱をベースにしたハンセンの溶解度パラメータのうち分極項(dP)や水素結合項(dH)は０以下にはなりません。

しかし通常の解析ソフトでは非極性の官能基の重回帰係数はマイナスになり、答えが負になってしまう事があります。

そのような限界値を持つ物性値は通常の重回帰のソフトウエアーでは解析できません。
化学の問題であって、数学の問題では無いからです。

簡単に説明すれば、例えばある化合物のlogSの計算値が４だった場合、実験値のlogSは２.0であるので、誤差は(2.0-4.0)/2.0,つまり-100%の誤差があると考えてしまいます。

その誤差を最小二乗法で最小にしようと働くので、計算値（誤差の自乗は100*100）を小さくするように重回帰係数に補正をかけて行きます。

そこで、logS=2.0近辺（つまり水への溶解度が非常に大きな化合物群で）重回帰係数は意味をなさなくなります。

また、測定限界の問題もある。昔のデータでは溶解度の測定データは10mg/100mlが限度でしたが、機器分析の発展でさらに低濃度の測定が可能になってきています。

10mg/100mlが実は0.01mg/100mlであった場合、logSでは値が1000倍（logSにして3）異なります。

その誤差を最小二乗法で最小にしようとするとやはり重回帰係数は大きな矛盾を持ってしまう事になります。

そこでlogSの推算式を構築しようと思った場合にはこうした事への対応ができるソフトウエアーの利用が不可欠になります。

こうした分野はケモメトリックス（化学計量学）と呼ばれる分野です。
化学的な情報は一般的には化合物の構造に蓄えられています。

その情報を引き出し、解析を行うには、一般的な解析ソフトではかえって本質を見失ってしまう事もあります。

そこで、[化学者の、化学者による、化学者の為のソフトウエアー]の開発が不可欠になるというのが私の立場です。
2021.5.28
MAGICIAN養成講座に参加している学生が、GROVE解析ツールを作成してくれました。それを用いて水への溶解性を推算する式を作成すると次のようになります(https://www.pirika.com/Education/JP/ChemoInfo/GroupContribution.html)。

「ある限界を超えた場合に誤差を誤差と見なさない」というアルゴリズムを加えた重回帰法の自作のプログラムを使って先ほどのデータを解析すると、以下のようになります。

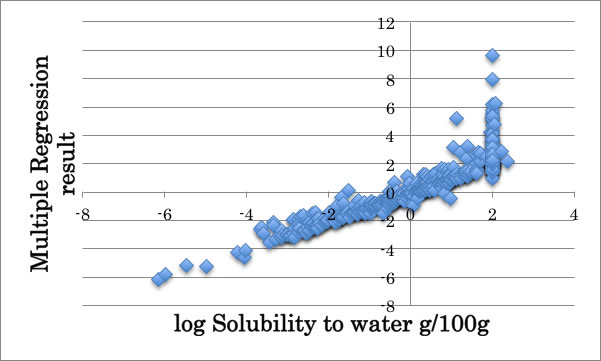
実験値が２以上のものについては、２以上であれば値が幾つでも誤差はないと判断するのでこのような結果になります。

課題：情報系の学生は、どのようなプログラム上の処理をすれば、このような計算ができるか考えてみましょう。

実験系の学生は、入力データにどのような小細工をすると同じような結果が得られるか考えてみましょう。

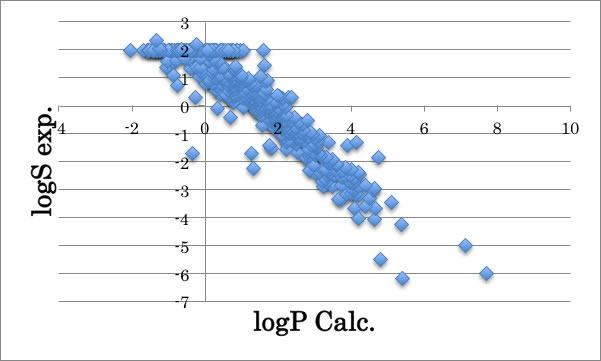
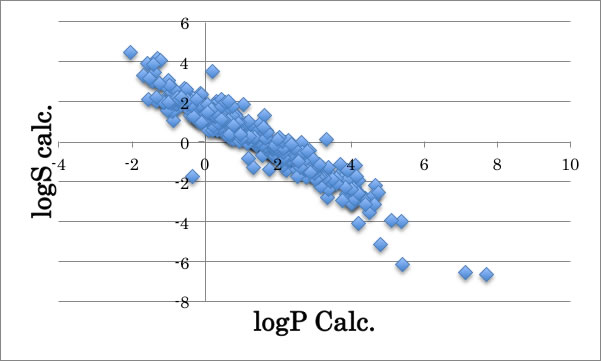
logP（オクタノール・水分配比率）の計算値とlogSの実験値をプロットすると上図のようになり、比較的高い相関がある事が知られています。

そこで、おおよそのlogSの値を予測したい場合にはlogPの値が使えることがわかります。

それにしてもlogS>2の領域の推算をlogPから行うのは無理そうなことは明らかでしょう。

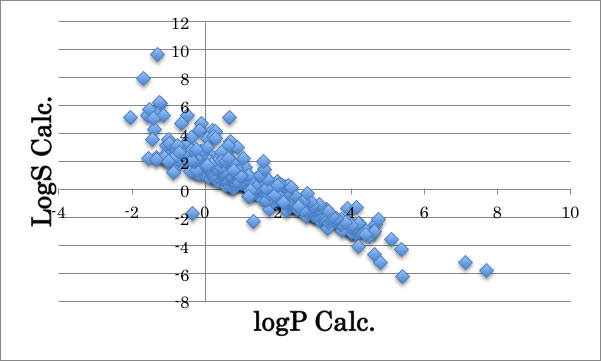
ところが、logS＞2.0を誤差と見なさないとういうアルゴリズムで計算したlogSとlogPの計算値をプロットすると上図のようにlogS>2.0の領域で大きく改良されるのが解るでしょう。

また、研究によっては良く溶解する化合物の精度を高めたい場合と、溶けにくい化合物の精度を高めたい場合があります。

通常の統計解析用のソフトウエアーでは「ある注目している領域の精度を高める」などという機能はついていないものがほとんどです。

例えば水に良く溶ける領域で精度を高め、logPとの相関を検討すると次のようになります。

左上の領域が改善され、その分右下の領域が悪くなる事が解るでしょう。

課題：ある領域の精度を上げる方法を、プログラムの作成上、もしくは入力データの処理から考えてみましょう。

それでは、こうしたアルゴリズムによって重回帰係数はどのように変化するのか見ておきましょう。

No	Functional Group	Normal MR	Max limit2	MaL2P
1	CH3	-0.533	-0.523	-0.515
2	CH2	-0.240	-0.273	-0.571
3	CH	-0.184	-0.224	-0.576
27	OH	1.670	2.027	1.584
30	O	1.519	1.588	1.265
32	C:O	1.815	2.046	1.357

普通に重回帰(Normal MR)をしたものを最初のカラム、logS>2以上を誤差と見なさない(Max limit2)を２番目のカラム、logS>2を設定し、かつ。溶解度の高い領域での精度を上げた場合(MaL2P)を３番目のカラムに示してあります。

CH3の重回帰係数はほとんど変わりませんが、MaL2P でCH2やCHの重回帰係数はマイナスが大きくなっています。

これは、溶解度の高い領域の化合物中のCH２、CHが正しい値を返すようにしたため、このような値になっています。

この係数を用いて、逆に溶解度が低い炭化水素を計算すると精度が低くなってしまいます。

アルコール、エーテル、ケトンを比べるとNormal MRではケトン、アルコール、エーテルの順になるが、MaL2Pではアルコール、ケトン、エーテルの順になり、納得しやすいでしょう。

Max limit2でlogS>2以上を誤差と見なさないと、アルコールとケトンはエーテルに比べ大きな値になります。

どの答えが正しいのか？　良く質問される。

それは重回帰式をどう使いたいのか次第なのですが、なかなか理解してもらえません。

しかし、重回帰計算をExcelでやっている限り答えは１つ（正確には、原点を通るというオプションがあるので、２つ）しか出てきません。

Mathematicaを使おうが他の統計解析ソフトを使おうが、それらは化学的物性値の特性をどこまで考慮してくれているかは常に気に留めておきましょう。

そして入力をどう工夫すれば目的の推算式が手に入るか頭を働かせましょう。

またもう一つ大事な事は、大きく外れる化合物がどんなもので、データの入力間違いが無いか、データの単位が間違っていないか？　他のデータ値が無いかをチェックしましょう。

次に、前述したアミノ酸のような官能基を複数持つ化合物の水への溶解度を考えてみましょう。

課題：ある官能基とある官能基が相互作用して溶解度が大きく変化する現象があるとした時に、プログラム上どう工夫をすれば、入力データ上どう工夫をすれば官能基のペアを特定できるか、考えてみましょう。

最初のテーブルに２級の水酸基も付け加えて拡張します。

これを、通常の重回帰法をつかって計算します。
logS=-0.641*CH3-0.143*CH2+0.430*CH+0.669*OH +0.775*2OH +1.159*O +1.471*C=O +0.186

結果を図示すると以下のようになります。

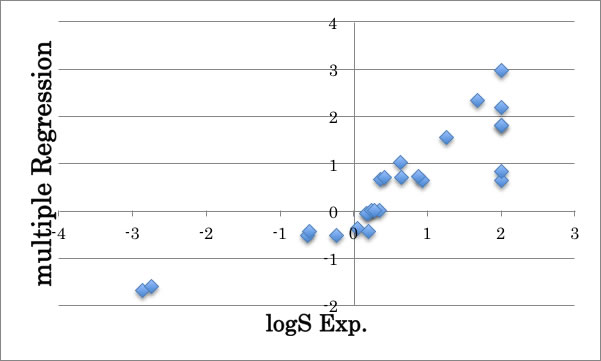
官能基の相互作用があるとして、OHとエーテル、２級OHとエーテル、エーテルとケトンの３種類を試しに使ってみます。

重回帰係数は以下のように求まる。
logS=-0.724*CH3-0.198*CH2+0.501*CH+1.033*OH+0.629*2OH+1.393*O+1.73*C=O -0.333*OH*O+0.249*2OH*O -0.596*O*C=O+0.218

１級OHとエーテル酸素を掛けたOH*Oの係数はマイナスで溶解度を下げるが、２級OHとエーテル酸素を掛けた２OH*Oの係数はプラスなので溶解度を上げる事がわかります。

ここで使った３種類は水溶性の高い官能基なので、この補正項はlogS=2あたりの精度を（平均的に）改善する事が下図から明らかでしょう。

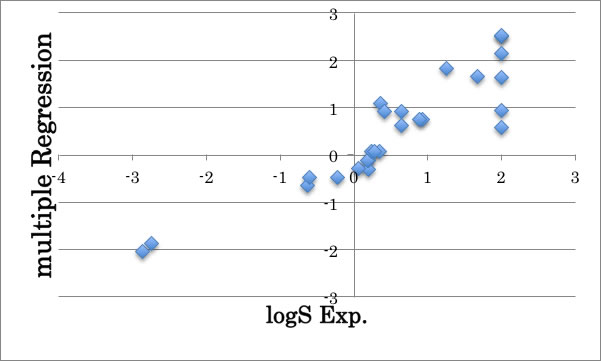
課題：現在Pirikaで使われる原子団は167種類定義されています。
官能基間相互作用は同じ官能基同士を含めれば、167*167種類存在します。
連立方程式を解く為には変数の数よりも式の数が多い必要があるので、官能基間相互作用は全てを入れる事はできません。

また連立方程式の中にその組み合わせが一つもないものもあるので、全ての組み合わせを評価する必要もありません。

どのような合理的選択方法があるか考えてみましょう。

この官能基間の相互作用を加味した重回帰計算を自動で行わせてみます。

OH	2.94	OH*OH	-0.55
2_OH	2.33
O	2.08	O*O	-0.30
C:O	2.43	C:O*C:O	-0.69

比較的低分子の溶媒の計算では、プログラムが選択した相互作用項の１例は上の表のようになります。

OH基が1つの時は、1*2.94 – 1*1*0.55 だけlogSを増加させます。
しかし、OH基が2つになると、2*2.94 – 2*2*0.55、
3つになると、3*2.94 – 3*3*0.55 となります。

OH１つあたりの溶解性は、分子が大きく、官能基が増えるにつれ減少して行くとプログラムが判断している事がわかります。

この効果はある意味、非線形性を導入したといういい方もできます。

しかし、同時に次のような相互作用項も求まるので、非常に有用です。

O*C2F5	-2.36		CH2*2_OH	-0.91
iso_Bu*C:O	0.46		CH:*O	-0.30

医薬品などにフッ素などのハロゲン原子を導入した時に溶解性がどう変わるのか定量的に評価する事が可能になります。

多くの研究では、水への溶解性は、そのままに、かつ、オクタノール・水分配比率を上げたいなどと、一見すると矛盾する答えを探したい場合が多いです。

現象が全て線形現象で、重回帰計算をすれば求まってしまうなら話は簡単です。

２つの線を描きその交点を求めるだけになります。

しかし、分子中にある原子団ペアがあった時に特異的に片方の物性値が変わり、もう一方に影響を与えないペアを見いだせば、ほかでは出せない特徴を設計する事ができます。

そこで、こううした非線形性や相互作用を定量的に扱う技術が非常に重要になります。

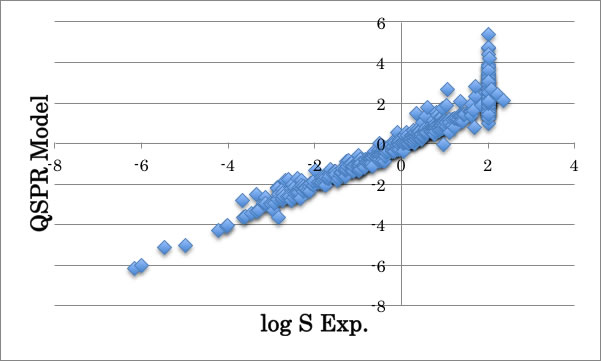
官能基間の相互作用を加味し、logS>2以上を無視すると指定して構築した最終のQSPR式の結果は上に示すような図になりました。

次に大事になるのは、
このモデル式でズレているのはどのような化合物かを特定し、どんな未知の力が働いているから結果がこうなったのか？を考える事です。

そうしたことを一つ一つ積み重ねる事によって溶解現象の本質に迫る事が可能になります。
その際にはlogSだけを見ていては駄目で、logP（オクタノール・水分配比率）、ヘンリー定数など様々な角度からの検討が必須でしょう。

課題：今回は溶解度をg/100gで評価したが、mol/100gで評価したらどうなるでしょうか？　

ここで解析したような比較的低分子の溶媒の場合には余り差が出ないでしょうが、医薬品の溶解度などでは入力データの工夫として重要なハンドリングです。

通常の溶解度で、100g溶質/100g水はlogS=2になるので、上限値の設定は容易でした。

しかし、溶解度をmolで扱うと、この部分の取り扱いが非常に難しくなります。

ここでは、logS<2となるグループでのlog molS の最大値と、logS>=2となるグループのlog molSの最小値から、しきい値は-0.17と設定し、上限界ありの重回帰計算を行ってみます。

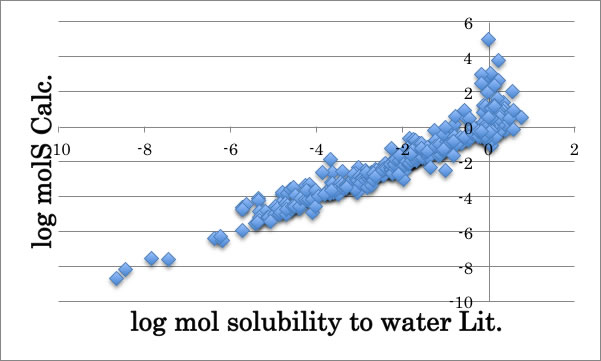
重回帰係数のテーブルを埋め、単純な重回帰係数との違いを議論しましょう。

	NMR	ML（-0.17）AE
CH3	-0.568
CH2	-0.235
CH	-0.174
OH	1.688
O	1.506
C:O	1.807

最近のMaterials Informatics(MI)ではRDKitを使って分子の識別子を生成させることが多くなってきています。RDKitを使った水への溶解度の推算式構築に関してはこちらをお読みください。最初143個のデータから推算式を作りました。

そのデータが1000個になるとこのようになります。
EPAのTESTには4000個を超えるデータが入っています。

推算式を構築する。より大きなデータセットに適用する。合わない。データ拡張。
それを延々と繰り返しているだけのような気がします。

目的を絞り、ドローンのようなマイクロ・AIを多数作るのも大事な方針だと思います。

水への溶解度を解析する方法論的には、ほとんどがPLSかPCAになってしまっていますが、試したところどちらもほとんど同じような結果しか与えてくれません。詳しくは、PLSとPCAのページで確認してください。

私がMAGICIAN養成講座で教えている事は、このページに書いてあるような機能を実装したような、「化学者の、化学者による、化学者のための」ソフトウエアーを作成していかないと本質が見えてこないという事です。

GROVE解析ツールを用いたlogKowの推算のページも参照してください。