2024.7
解析例トップ >
次世代HSP技術 >
2017年のHSP50周年記念公演の際に、私は、dD項の分割とdH項の分割を提案した。しかし、
HSP距離＝sqrt(4*(dD1-dD2)2+(dP1-dP2)2+(dH1-dH2)2)
と言ったような、全ての系に使えるシンプルなHSP距離は作れなかった。
そこで、一般ユーザー向けではないが、MIで使う用の(GUIなど考えない）HSP距離の式をデータ駆動型で導いてしまえ、ということに取り組んだ。（今年の横浜国大の授業を最後に、大学関係からは隠遁する。そして終了後の最初の取り組みで２週間ぐらいかかった。）
2017年の時点で分かっていたことは、dDをdDvdwとdDfgに分割すると距離の式でdDの前の4というファクターが要らなくなるということだ。
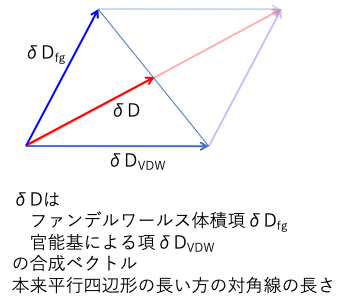
新しい距離の式は=sqrt((dDvdw1-dDvdw2)2+(dDfg1-dDfg2)2+(dP1-dP2)2+(dH1-dH2)2)となる
dDvdwは分子の大きさに依存する項であるので、例えばポリマーの溶解性にはあまり必要ない。ポリマーはユニット・セルのファンデルワールスの大きさはあるが、実際の大きさは意味がないので
(dDvdw1-dDvdw2)2はなくても精度が出ることは確認した。
距離の式=sqrt((dDfg1-dDfg2)2+(dP1-dP2)2+(dH1-dH2)2)
dD関係で3種類の式が作れる。
また、dH関係に関しては、AbrahamのAcid, Baseを元にdHacid, dHbaseを定義していた。しかし距離の式への落とし込みが難しかった。
結局、HSPiPに搭載されたのは、(dHacid1-dHacid2)2 + (dHbase1 – dHbbsae2)2というEuclid Typeの距離の式だけだった。（探索がClassic Hansenのみなのでかなり変な答えを返す）
例えばカルボン酸はダイマーを作る。
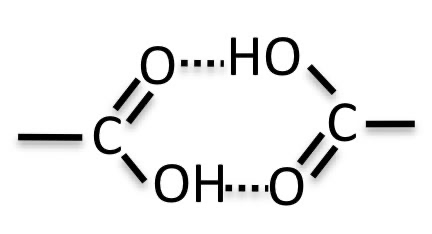
カルボキシル基は、dHacidとdHbaseの両方の値を持っているので、一種の塩である。
弱酸の塩に強酸を入れると交換が起きる。
それを表現するのが、Beerbowerの式で、次の式になる。
coeff*(dHacid1 – dHacid2) * (dHbase1 – dHbase2)
溶質のdHacid2, dHbase2に対して、溶媒のdHacid1, dHbase2のどちらかが大きければ式がマイナスになり、距離が短くなる。
しかし場合によるとルートの中がマイナスになってしまう。
取り扱いが難しいので使われていなかった。
極性項という意味で、ドナー/アクセプターはdPまで含むのか、どうか。それは今後の課題であるが、今回はdP項だけは一つにした。
dH項は６タイプ検討した。
dHのみ、
dHacid, debase
dHacLa, dHbaLa(分子中で最も大きいdHacid, debaseを持つ官能基の値）
yED, yEA (YamamotoのElectron Donor, Electron Acceptor: HSP50で発表)
yEDLa, yEALa (分子中で最も大きいyED, yEAを持つ官能基の値）
Laを使うのは、例えばカルボン酸のpKaは分子のサイズにはよらずにほぼ一定になる。
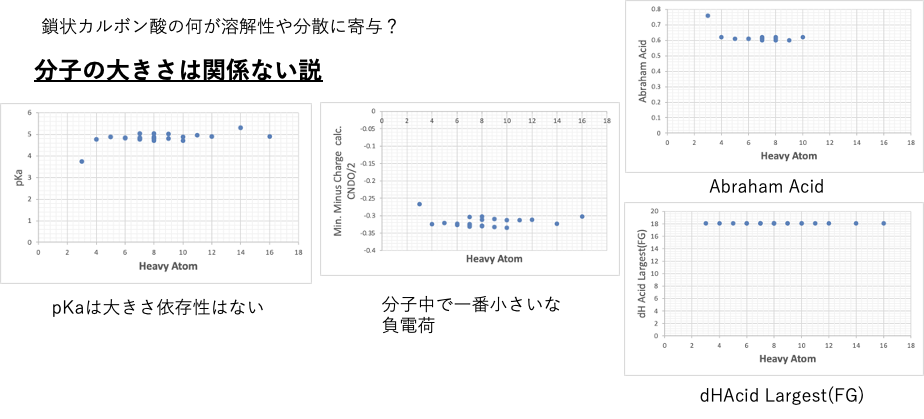
そのような物性が溶解性に影響を与えるなら、dHacLaを使った式の時にパーフォマンスが高くなる。
dD３タイプ、dH6タイプ、Euclid Type、Beerbower Typeを片っ端に評価するWebアプリを作成した。MIユーザーには提供を始めた。詳しい話はPirikaNews202407を参照してほしい。
例題として、HSPiPに付属しているe-Bookの量子ドットのデータを用いる。
（量子ドットについては、ビデオ・チュートリアルも作ってある。）
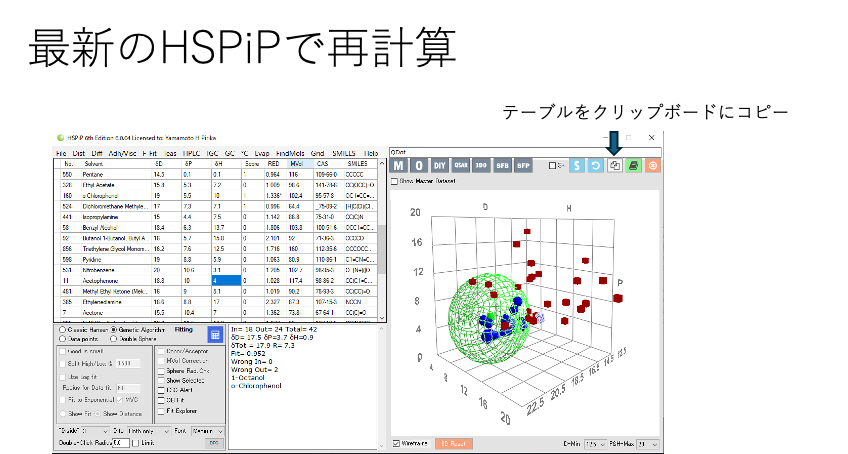
QDot.hsdxをHSPiPに読み込む。
左側のテーブルをクリップボードにコピーしエクセルなどに貼り付ける。
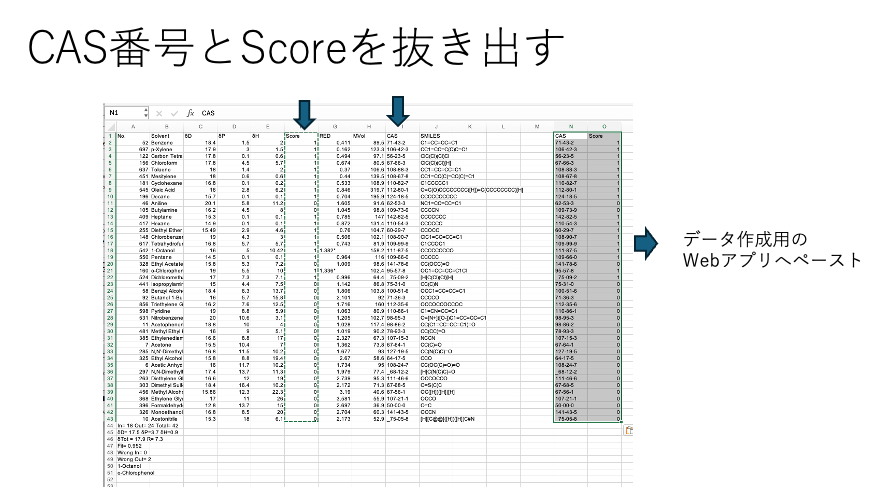
CAS番号とScoreを抜き出し、データ作成用のWebアプリにペーストする。
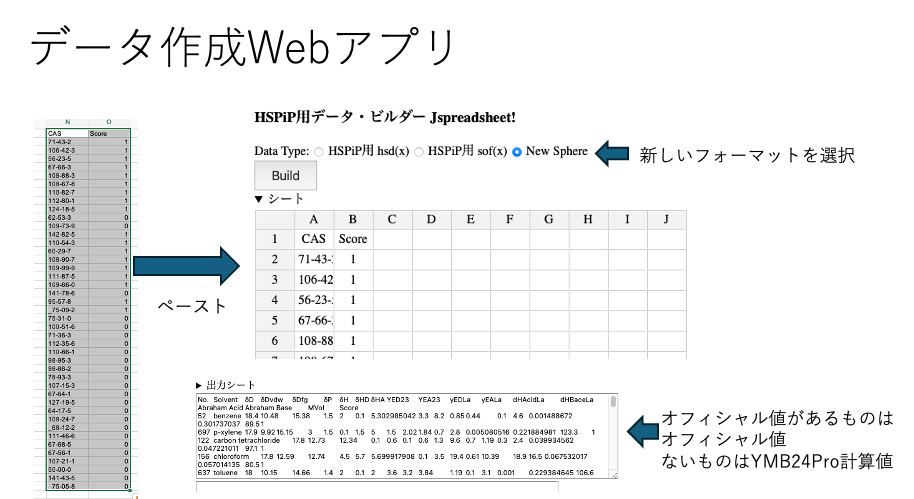
Webアプリでは新しいフォーマットを選択する。
アプリはオフィシャル値のあるものはそれを使い、無いものはYMB24Proの計算値を使い入力データを作成する。
新データフォーマットはタブ区切りのテキスト・データなので取り扱いは容易だ。
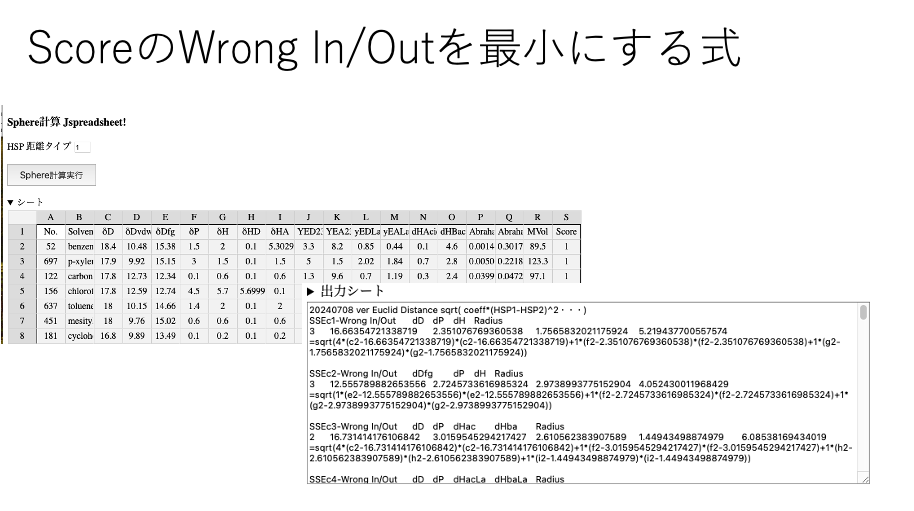
あとはScoreのWrong In/Outを最小にする式を作成するWebアプリにデータを流し込むだけだ。
全ての組み合わせの33式でWrong In/Outを最小にするパラメータを決定した。式の一部は以下のようになる。
Euclid Type
1: sqrt(4.0*(dD1-dD2)^2+(dP1-dP2)^2+(dH1-dH2)^2)
3: sqrt( 4.0*(dD1-dD2)^2+(dP1-dP2)^2+(dHacid1-dHacid2)^2+(dHbase1-dHbase2)^2)
13: sqrt((dDvdw1-dDvdw2)^2+(dDfg1-dDfg2)^2+(dP1-dP2)^2+(dH1-dH2)^2)
14: sqrt((dDvdw1-dDvdw2)^2+(dDfg1-dDfg2)^2+(dP1-dP2)^2+(dHacid1-dHacid2)^2+(dHbase1-dHbase2)^2)
2: sqrt((dDfg1-dDfg2)^2+(dP1-dP2)^2+(dH1-dH2)^2)
5: sqrt((dDfg1-dDfg2)^2+(dP1-dP2)^2+(dHacid1-dHacid2)^2+(dHbase1-dHbase2)^2)
Beerbower Type
19: 4.0*(dD1-dD2)^2+(dP1-dP2)^2+coeff*(dHacid1-dHacid2)*(dHbase1-dHbase2)
29: (dDvdw1-dDvdw2)^2+(dDfg1-dDfg2)^2+(dP1-dP2)^2+coeff*(dHacid1-dHacid2)*(dHbase1-dHbase2)
21: (dDfg1-dDfg2)^2+(dP1-dP2)^2+coeff*(dHacid1-dHacid2)*(dHbase1-dHbase2)
23: 4.0*(dD1-dD2)^2+(dP1-dP2)^2+coeff*(Y-ED1-Y-ED2)*(Y-EA1-Y-EA2)31: (dDvdw1-dDvdw2)^2+(dDfg1-dDfg2)^2+(dP1-dP2)^2+coeff*(Y-ED1-Y-ED2)*(Y-EA1-Y-EA2)
Beerbower式は式や半径がマイナスになることがあるのでsqrtは取らない。
3次元以上が多いので、溶解球とその半径という概念は使わない。式と閾値になる。
Wrong In/Outを最小にする式は次のようになる。
Euclid Type式
14：SQRT((dDvdw-13.98)^2+ (dDfg-16.9)^2+ (dP-2.7)^2+ (dHacid-2.7)^2+ (dHbase-1.39)^2) Wrong In/Out 1
Beerbower Type式
25：(dDfg-14.6)^2+ (dP-2.2)^2+ 0.0978*(yED-9.04)*(yEA-6.37) Wrong In/Out 0
量子ドットの表面は修飾されている割に、dHacid/dHbaseやyED/yEAが効果が高いあたりは興味深い。
こうしたデータ駆動型の研究は、唯一無二の理論式を作るものではない。
Wrong In/Outが小さい方が良いモデルとも言えない。
一般的なHSPiPユーザーに提供しているアプリでもない。
この系に特化して何が起きているのかを考察するために行う。
MIst用の特別なツールである。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください