2024.12.23
情報化学+教育 > MAGICIAN 養成講座 >
HSPの解析例トップ > 次世代HSP技術 >
pirika.comで化学 > 化学全般 > 高分子化学 >
電子線レジストポリマーのGs(100eVあたりの主鎖切断数）予測に関してはブログにもかいた。現像液の設計に関しては、「QSphere：量的な問題を解く」で解説した。
半導体用レジストポリマーの現像液設計（溶かさない溶媒設計）というv-tubeのビデオもある。
MOOCにも大学で行った講義を置いてある。大学での講義は簡単に言ってしまえば、次のようなポリマーがあったとき、100eVの電子線で何個の結合が切断されるか予測式を作ってみよう、というものだ。2011年の授業で話をした。
赤文字の会社は横浜国大の学生が就職している会社だ。将来そんな会社に就職してレジストポリマーの設計をやるとしたら？その時に覚えていた方が良い技術を勉強した。
今回は、エステル系に限り、さらにポリマーハンドブックからポリマーを継ぎ足し解析してみる。各ポリマーのポリマーSmilesの構造式を用意した。ポリマーSmilesを分子のお絵かきソフトJSMEで得る方法はこちらから。
ここまで準備できたら、後はYMB24Pro4MIにjobを投げ込むだけだ。YMB24Pro4MIはWebアプリを独立実行型(EXE)にしたものだ。Mac版、Windows版、Linux版がある。YPB-24を選択すると次の画面になる。
Data TypeはYPB24Proを選択する。Polymer Smilesで作成した４列を入力の部分にペーストし、計算実行ボタンを押す。Polymer Smilesを１つづつ解析し、ハンセンの溶解度パラメータ(HSP)を含め様々な物性値を推算する。この物性値を使ってMI計算を行う。
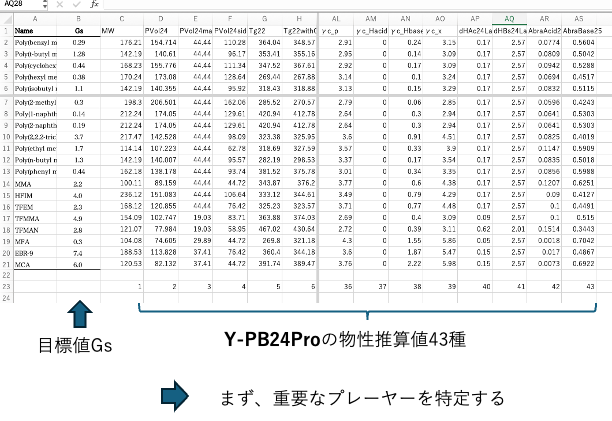
Pirikaで使うツールは１列目名前などで、２列目には目的変数、教師データを入れる。ここでは２列目がGsになる。その後ろに説明変数43種類が付け加わったテーブルが瞬間で作成できる。
これができたら、まず、メジャープレーヤーを特定する。
YMB24Pro4MIで拡張相関係数計算ツールを選択する。
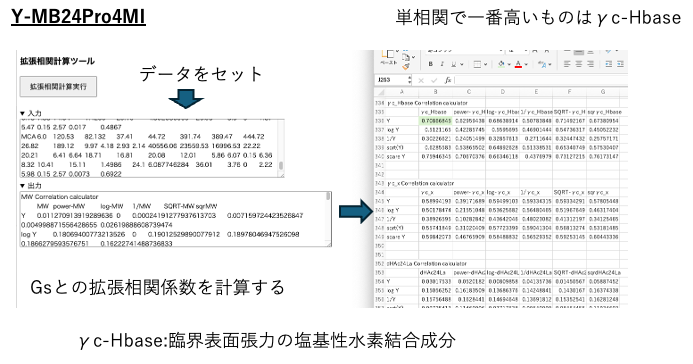
これは、Gsと43種の説明変数の単相関を計算する。その時に変数の、logをとったり、1/X, sqrt(X)などを計算したうえでの相関係数を出力する。ここで最も高い相関係数となったものは、γc-Hbase:臨界表面張力の塩基性水素結合成分であった。Y-PB24Proでは臨界表面張力(γc)をHSPと同じように分散項(γc d)、分極項(γc p)、水素結合項(γch)に分割する。この水素結合項を更に酸性成分/塩基性成分に分けたものだ。これは、接触角を推算できるように新たに付け加えられた物性値である。
メジャープレーヤーが特定できたら、次は重相関を検討する。
YMB24Pro4MIで変数選択重回帰法を選択する。
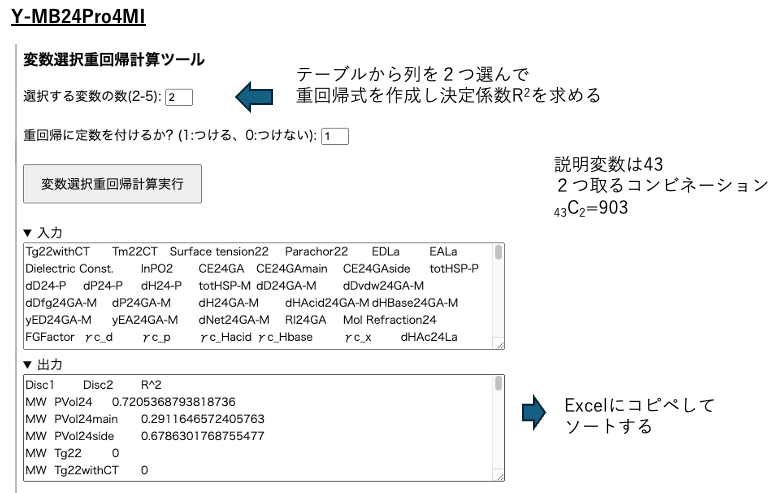
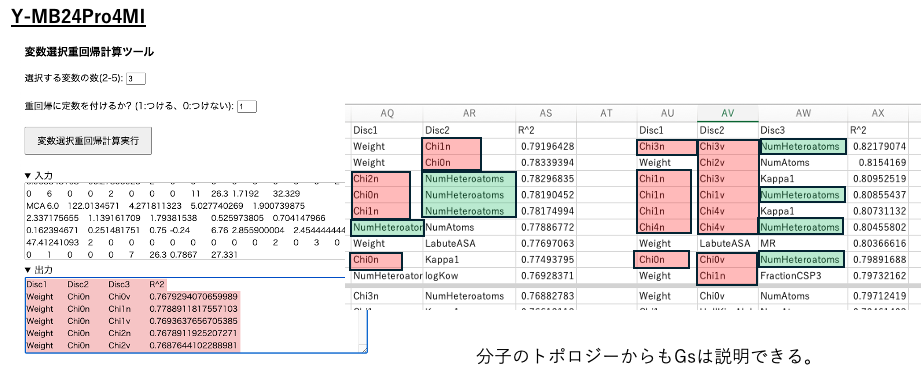
説明変数は43種類あるので、2種類の列を選ぶには43C2で903種類ある。この903個の組み合わせを全て重回帰計算する。そして決定係数R2と共に出力する。ソートはされていないので、エクセルに戻してExcelで大きい順に並び替えをする。
同じように変数を３つ選んで変数選択重回帰を行う。列数は5つまで選べるが、CPUの性能、メモリーの量次第でとても時間がかかったりする。2-3ぐらいが妥当なところだろう。
R2が大きい順に並び替えられていると、どんな列を選んだらGsの大きさを記述できるか定量的に理解することができる。
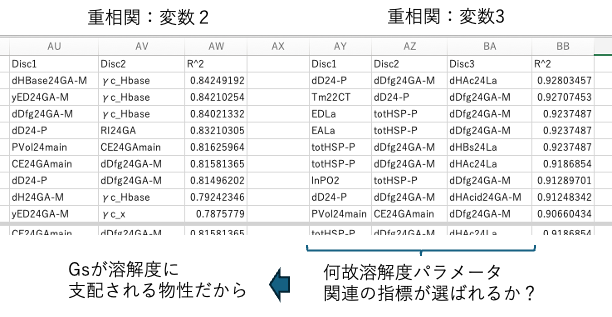
特に変数を3つ選んだ時には、溶解度パラメータ関連の変数が多く選択される。この事はGsが溶解度パラメータに支配されていることを示している。これは一見すると意外だ。レジストポリマーを現像する時の溶媒選択にはHSPはとても良く使われている。しかし、電子線を当てて結合を切断している時に溶解度パラメータはどう効いているのだろうか？
そこで、YMB24Pro4MIで重回帰法を選択して、まずはGsの文献値と重回帰計算値を比較してみる。
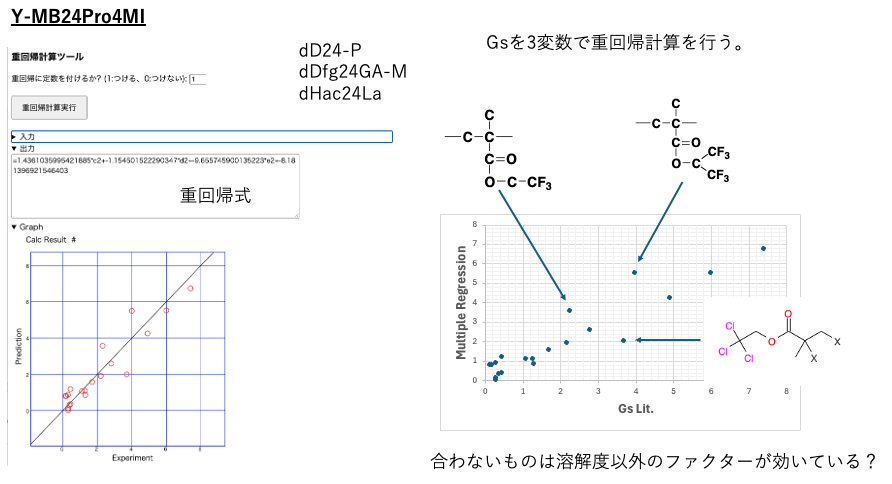
３つほど大きく外れるハロゲン系のポリマーがある。これは溶解度パラメータ以外のファクターが効いているのかもしれない。しかし残りのポリマーはとても良く溶解度パラメータで記述できている。
溶解度パラメータは次式で評価することができる。
溶解度パラメータ=(凝集エネルギー(Cohesive Energy)/Unit Volume)0.5
そこでY-PB24Proの吐き出す物性値のうちCohesive Energyの推算値とGsを比較してみる。大きく外れるものが3つあるので単相関は大きくないが、他はかなりきれいな相関がある。
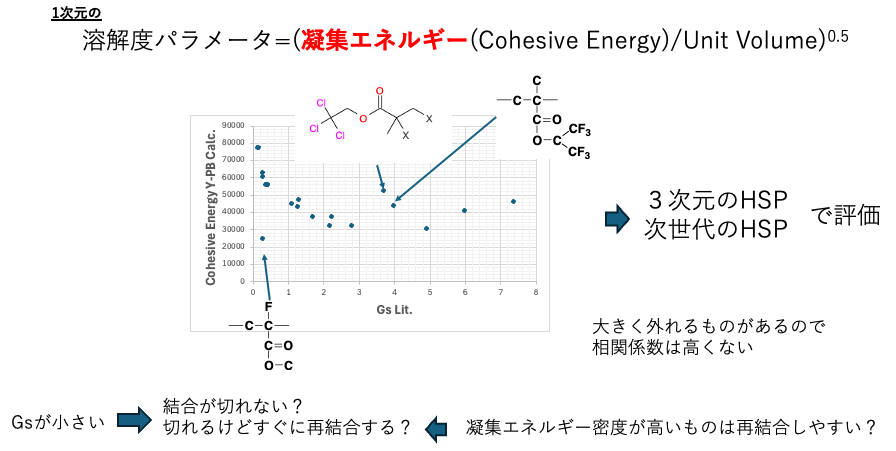
凝集エネルギーとGsがこのような相関があるということは、凝集エネルギーが高いポリマーは電子線で結合が切れないか、切断されてもすぐに再結合してしまう事を示唆している。この場合のSP値は1次元のSP値になる。そこで、これを3次元(n次元）のハンセン溶解度パラメータで評価する。
次世代HSPのSphere計算用のデータフォーマットを作成するにはYPB24ProでNew Sphere計算用のラヂオボタンを選び実行する。
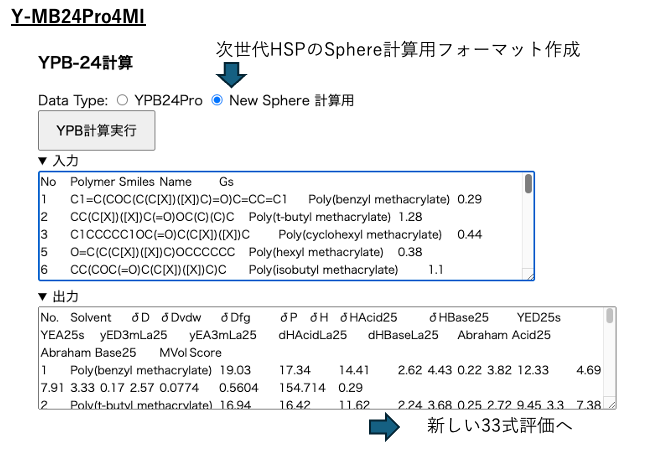
得られた出力をエクセルに戻しておく。
新距離の33式計算ツールは、YMB24Pro4MIの中にあるように記載してあるが、別のソフトウエアーになっている。これは計算がとても重く、計算時間がとても長くなってしまったので、別にした。並列計算を行うようにWorkerを利用して高速化を図っている。
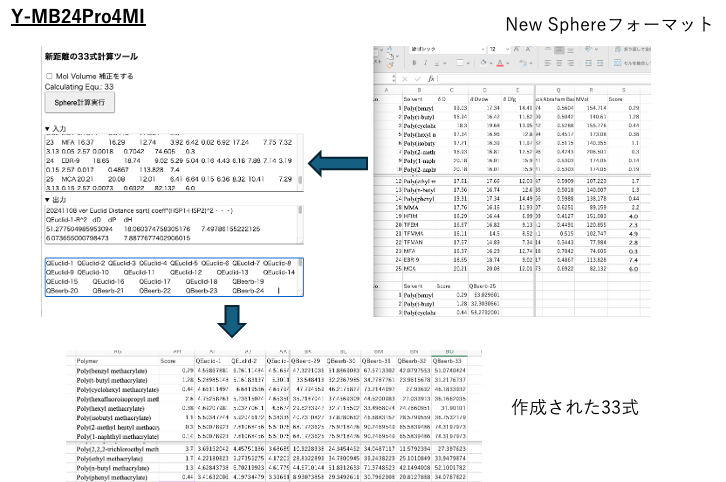
New Sphereフォーマットのデータを33式計算ツールにペーストし計算を実行する。
計算が終わるまで5分ぐらい待つ。
待っている間に、ハンセンの溶解度パラメータ(HSP)の距離について確認しておこう。
HSPは3次元のベクトルで表すことができる。変な係数４が付くが、3次元空間にプロットすると空間中の位置がわかる。そして、ハンセン先生が基本を作られた、Sphere法が球の中心を定める。この球の中心とベクトルの終点との距離をHSP距離と呼ぶ。当然、4次元以上のSphereは球にはならないので、式の内側、外側という定義になる。
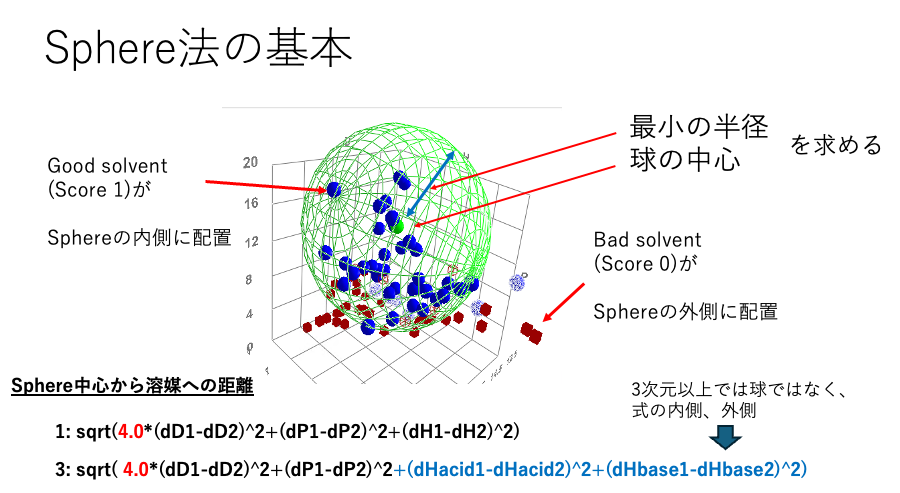
このSphere中心からのベクトル距離と物性値の間には明確な相関が存在する場合がある。
私は次の関係を唱えている。
HSPベクトルが似ている(空間上の似た位置にいる）ものは、似た性質を持つことがある。そしてその性質は中心からのスカラー距離が大きくなるに連れ弱まる。
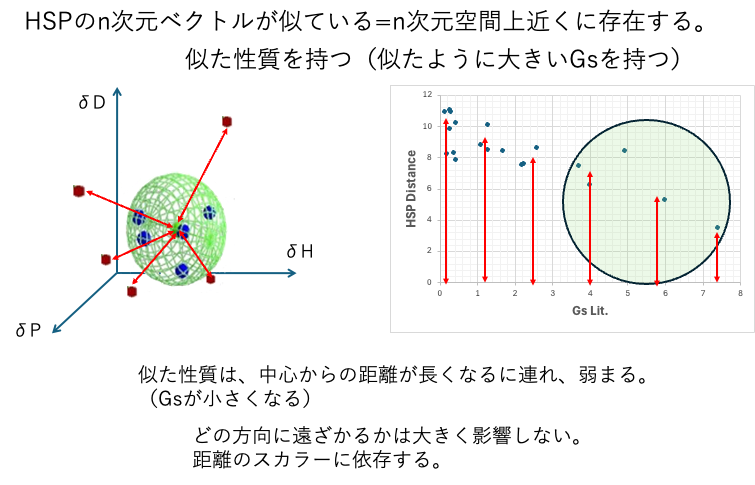
例えばポリマーの溶解の時には、良溶媒が集まって球(Sphere)を作ることもある。しかし、良いとか悪いというのは、研究者の主観である。都合の悪いものが集まることもある。
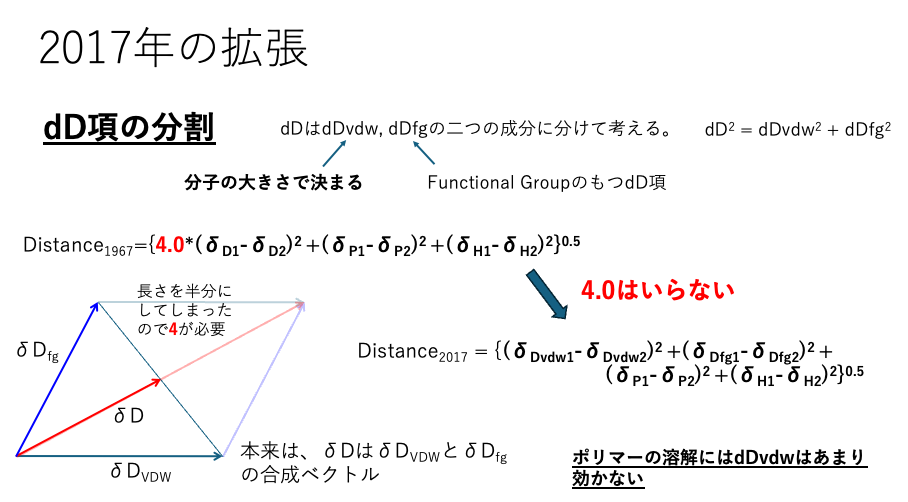
このSphere法を、私（山本博志）が2017年に拡張した。まず、dD項の分割だ。オリジナルのSphere法の距離の式にはdDの差分の前に４というファクターがある。
熱力学的にこの４の意味を説明できないので、常に攻撃の対象になった。
例えば、希ガスは、分子同士の相互作用は無いと考えて良い。しかし、希ガスであっても、沸点はあるし蒸発潜熱も持つ。そこで、分子で大きさを持つものは、分子の大きさに応じた、ベースのSP値を持つとする。これをdDvdwと呼ぶ。オリジナルのHSPはベースを直鎖炭化水素に置いた。しかし直鎖炭化水素であっても、分子の大きさに加え、CH2の相互作用は存在する。それを官能基の相互作用としてdDfgと呼ぶ。本来この合成ベクトルがdDであったのだが、この長さを半分にしてしまったので、４という係数が必要になる。dDvdwとdDfgにした場合には係数はいらなくなる。
次に、水素結合項を分割した。以前からdH項はdHdo,dHac項（プロトンドナー、アクセプター）に分割されていた。ただし、酸、アルコール、アミンの活性水素を持っている化合物以外はdH項は全てdHacに割り振られた。カルボン酸、アルコール、アミンは酸でもあり、塩基でもある両性に分類される。
そこで、dHを分割する効果は殆どなかった。
2017年HSPの50周年記念講演会で私は、ブレンステッド酸／塩基ではなく、ルイス酸/塩基としての指標yED, yEAを導入した。（yamamoto Electron Donor/Acceptor）
この値は分子のSmilesの構造式から計算で算出できる。（HSPiPには搭載されていない。YMB24Pro4MI独自の機能だ）
HSPが、ナノ粒子のような金属を含むような系に利用されるにつれて、ブレンステッド酸での評価では好ましい結果を得られなくなってきた。HSPは基本的には、平均場理論で計算される。そこでアルコールは分子が大きくなるに連れ、水素結合項は小さくなる。しかし、分散現象がカルボン酸のpKaに依存する場合、pKaは分子の大きさとはほぼ関係ない（ギ酸だけ異常になる）。そこで分子中で最大の(Largest)ブレンステッド酸／塩基、ルイス酸/塩基の官能基だけを考慮する式も導入した。
また、弱酸/弱塩基の塩に対して、強酸、強塩基を入れると交換反応が起こることが知られている。それを表現するためには、Euclidタイプのタイプの式では不十分で、Beerbowerの提案した式を使った方が良い場合がある。この全てを評価すると33式になる。
HSPiPに搭載されているのは1式と3式だけでアルゴリズムは少し古い。
今回は全面的に書き直してYMB24Pro4MIに搭載した。
実際にどの式がどのような相関になるのかセレクターでチェックして確認してほしい。
ｄDの分割の効果を確認すると次のようになる。
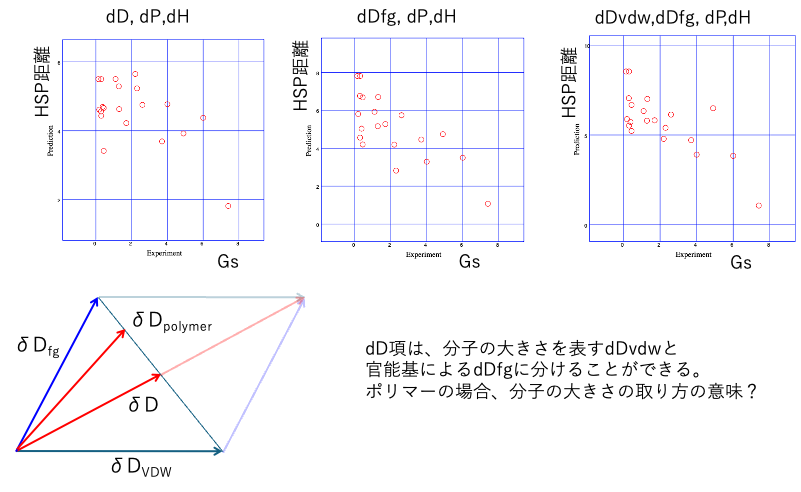
標準の[dD,dP,dH]ではHSp距離とGSの間の相関は低い。dDfgとdDvdw,dDfgどちらを取るかは意見の分かれるところかもしれない。
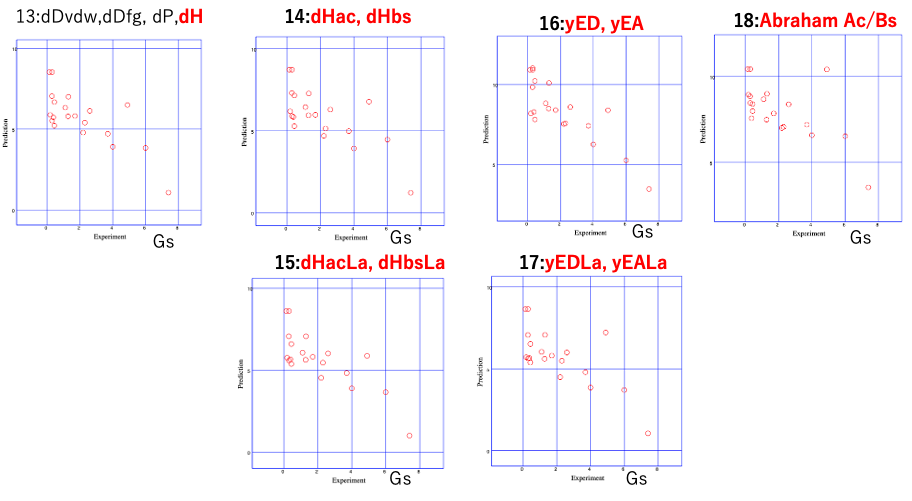
dHの分割に関しては、私なら16式か15式を取る。
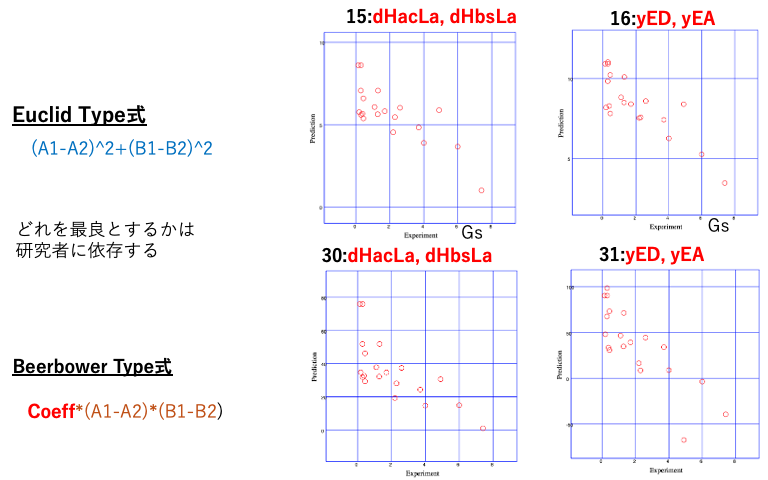
Euclidを選ぶかBeerbower、どちらを選ぶかと言われれば、悩ましいが16式を選ぶだろう。
電子線レジストポリマーの設計に関しては、昔KAISTで講演を行ったことがある。
その時には多田宰先生の論文を示したうえで、分子軌道計算以外にもHSPを使った解析もありうることを示した。
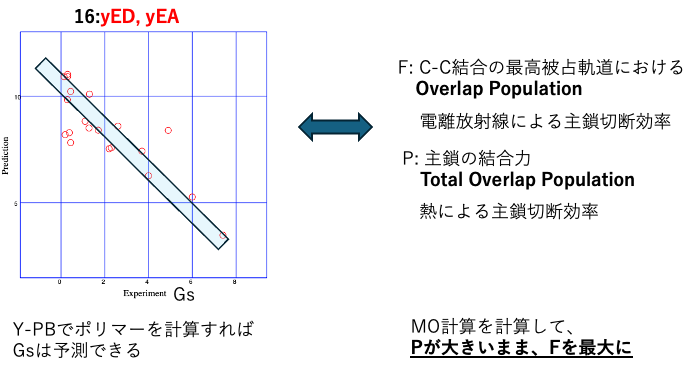
それから20年も経つと、こんな事は簡単に試すことができる。
YMB24Pro4MIツールのCNDO-QeQ計算ツールを選択する。
polymer Smilesの[X]を[H]に置き換え計算を実行する。
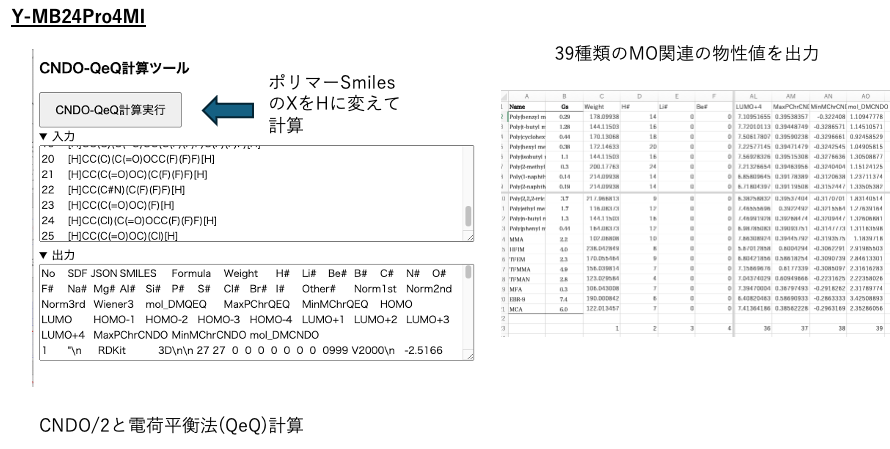
39種類のMO関連の物性値が得られる。
このテーブルを使って変数選択の重回帰を行う。
ダイポールモーメントや最小負電荷を使えば、決定係数0.89でGsを計算できる。
RDKit計算ツールを使えば同じく39種類のトポロジカルな物性値が得られる。
つまり、polymer Smilesがあれば、1Stopで多面的な評価を瞬間で行うことができる。
大事なのはこの点である。コンピュータの計算だけで、レジストポリマーを設計しようとした場合、(私の25年以上の経験から)どんなに決定係数が高い相関が得られたところで、所詮、データ数はビッグデータではない。データが増えた時に推算結果と合わなくなる可能性はとても高い。だからといってビッグデータ、ビッグデータと騒ぐなら、計算機屋さんとして失格の烙印を押される。華々しく論文は書いたけど、消えてしまう事が非常に多い。
その中で25年以上、この領域の研究者として企業で生き残れてきたのは、こっそり、こうした多面評価を行い、どんな列をどんな数使っても、結論は変わらないと自信を持てるまでいじくり倒して来たからだ。
MIと言えば分子軌道計算一択なんという研究者も多い。
MO計算はどんなポリマーも計算できるし、化学のこと知らなくても何となくデータは集まってデータサイエンスぽいことが直ぐにできる。まー、あと25年生き残れることを祈っている。
おまけに
こうしたポリマーは実は単独で使われることは少ない。例えばコポリマーにした時のGsの値が書籍に記載されている。
こうなってくると、pirikaはとても優位に立てる。
私は元々高分子屋だし、重合シミュレータ(POSEIDON)も開発している。
そこで、任意のモノマーの任意の組成での重合のシーケンス解析が可能になる。
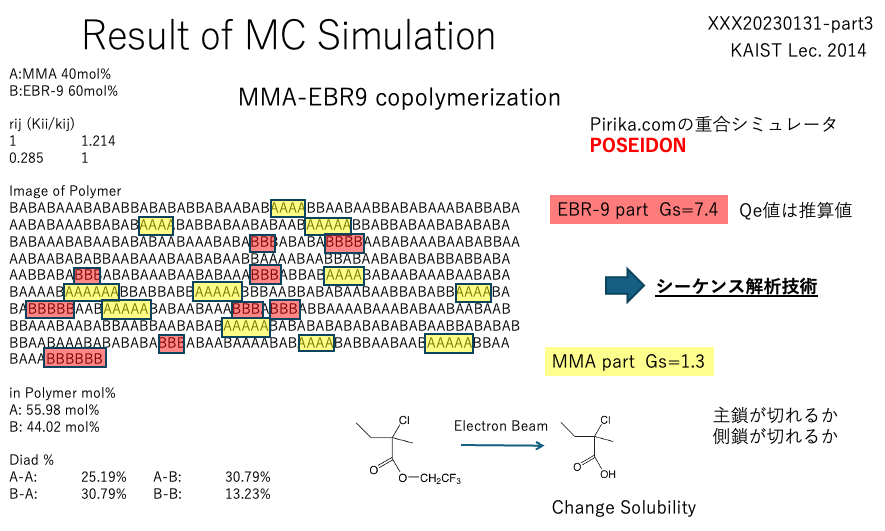
シーケンス解析をするためには、モノマーの反応性比やQe値が必要になる。
分子構造からQe値を予測するプログラム、実験をした結果からQe値を決定するプログラム。40年以上書き続けた化学系のプログラムを持つのが私の強みだ。
こうしたポリマー用のツール群はまた別途まとめ上げようと思う。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。