2025.1.27
情報化学+教育 > YMB Pro for MI >
注意:HSPiPに搭載の機能ではありません
21017年の拡張
HSP50周年記念講演会で次世代HSP2として水素結合項の分割にルイスの酸塩基を利用し始めた。2023年のドイツでのワークショップでも発表したように、無機物などの分散を評価する時はyamamotoのED、EAが有効だ。yEDとyEAは分子のSmiles構造式から推算する事ができる。
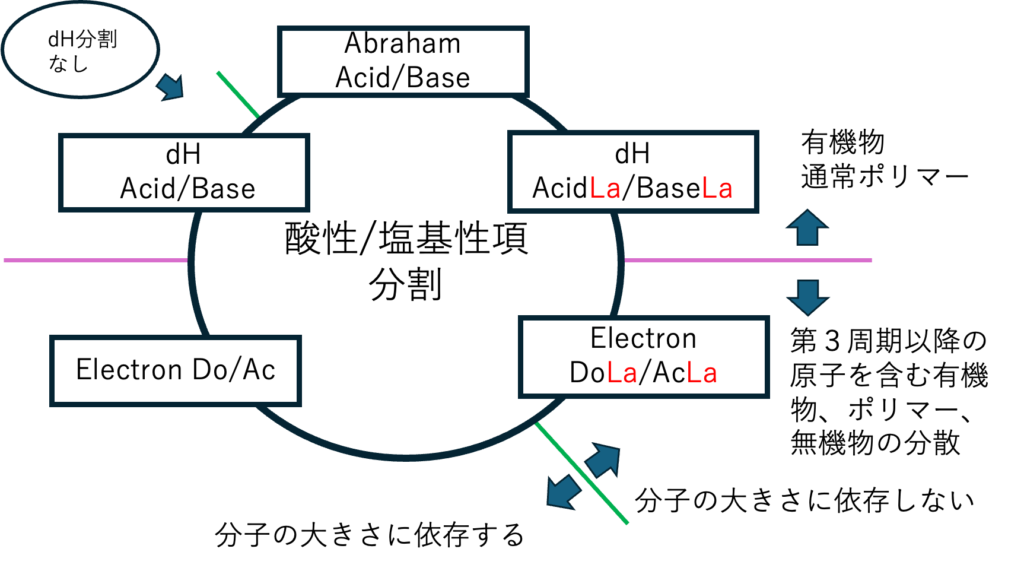
溶解度パラメータにED(Electron Donor), EA(Electron Acceptor)を持ち込んだのは私が初めてだと思っていた。Abraham教授のAcid/BaseからdHacid, dHbase分割を開発したのも私だ。
yED,yEAは次世代ハンセンの溶解度パラメータ(HSP2)の目玉としている。
このYMB Pro for MIでも使い方を、様々な例題を使って解説している。
この計算には時間がかかる。計算を待っている間に、本棚の本をペラペラ眺めていた。
1991年の書籍。
Acid-Base Interactions: Relevance to Adhesion Science and Technology
Frederick M. Fowkes (1915-1990)

ガックリだー。なぜ気が付かなかったのだろう?
18式ではHSPのうち分散項(δd)とDN(ドナー数), AN(アクセプター数)の線形式で溶媒の種類によって変わる物性値の推算式が作れるとある。
まー、35年遅れなら、悔しいとか、そんなレベルでもない。
ある意味、僕が開発を進めている、YMB25Pro4MIの正当性が保証されたようなものでもある。私の式では、Fowkesの式と異なりδPの項が残っているが、取り敢えず何か極性を示すパラメータで、δD、δP、ED, EAの評価をしてみる。
誘電率を計算してみる
MO計算は基本、真空中の1分子の話だ。でも誘電体モデルとか言って、ある指定した誘電率の空間中での計算を行う事ができる。
では、溶媒の誘電率はどうしたら推算できるだろうか?
基本的には極性の高い溶媒は誘電率が高い。しかし極性って何だろう?ダイポールモーメントか? しかし完全に対称な化合物、N#C-C#Nはダイポールはゼロになる。
これまでに何度も誘電率の予測のQSAR式にトライしてきたがあまり上手くいっていない。分子の3次元構造とその集合体がうまく表現できていなかった。
データの作成法、距離の式の求め方を説明
書いて説明するのは難しいのでV-tubeを作った。
動画の説明
次世代のハンセンの溶解度パラメータ(HSP2)では、多面性評価を行います。分散項を2つに分割し、水素結合項も5パターンに分割します。 しかし、やることは簡単です。化合物のCAS#と解析したい物性値をExcelの上に準備します。CAS#をコピーしYMB24Pro4MIを使いデータ変換します。 CAS番号からSMILESの構造式、名称などをDB検索し入力データを作ります。このデータを使ってNew Sphere用のデータセットを作成します。今回はYMB25Proを使って推算値の拡張HSPデータを使います。 これを一旦Excelに戻し、再びコピーし、距離の式計算アプリで最適距離の式を求めます。5コアを使って並列で計算を行います。 この距離の式は、使った物性値と距離の式が最も高い相関になるように係数が算出されます。 距離の式をエクセルに戻し、結果をビュワーにペーストすれば、各式がどのようなパーフォマンスになるかを調べることができます。 YMB24Pro4MIはこうした計算に必要なツールを全て含んだパッケージです。
誘電率と距離の式
実際に計算してグラフを描いてみると、とても相関が低かった。
これは典型的なケースで、誘電率をlogを取る事にする。(物性値の最小と最大が2けた変わるようなものはlogをとった方が良い場合が多い)
CAS番号と物性値があれば285溶媒のlog(誘電率)の計算は10分程度で終わる。(ビデオでは計算は端折っている)
そして、HSP距離と誘電率の関係はすぐに確かめる事ができる。
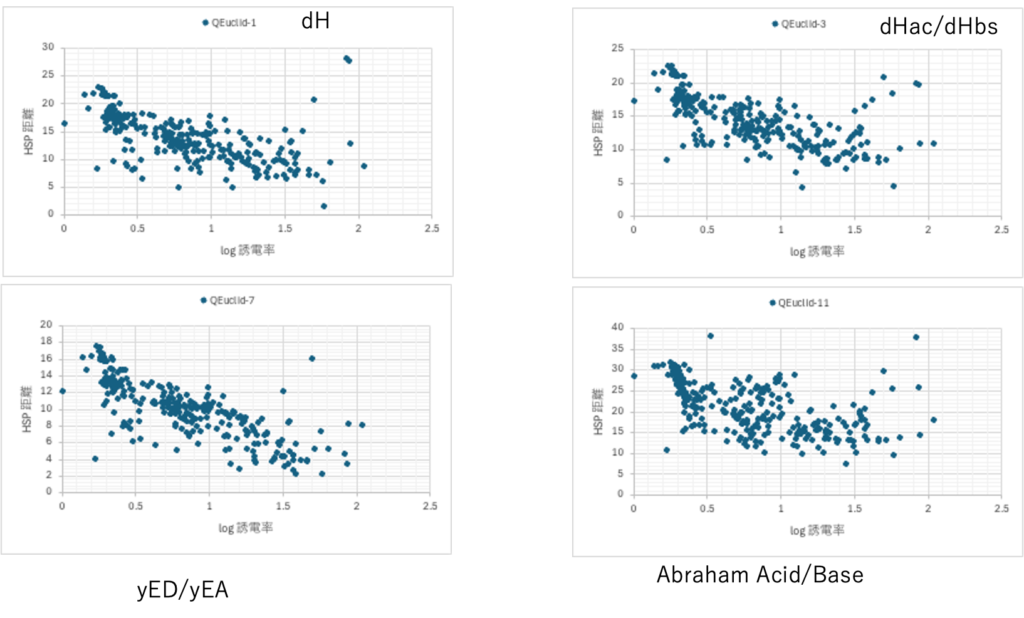
溶媒のCAS#と誘電率のデータあれば、グラフまで辿り着くのに10分とかからない。そして拡張HSP2と誘電率にはどのような関係があるのか数式で表現できる。
どの溶媒が大きく外れるのかデータをクリックすれば表示される。それが何故かを考察する事ができる。
もう暫くすれば、CASと誘電率をネットから集めてこいってChatGPTに頼めばすぐに一覧表を作ってくれる時代になる。私もCAS検索はChatGPTに頼んでいる。
HSP距離との相関まで全部やってくれるだろう。
原料を一番よく溶かし、反応速度が高くなるように誘電率の高い溶媒を設計して!って頼む時代。タイパが高くていい時代になったものだ。
暇な人間は何をするか
まー、俳句を作るとか。短歌を読むとか。
僕は、そうした心配はする必要は無さそうだ。
Fowkes(1915-1990)の本に書いてあった(18)式
P = P0 +α・DN + β・AN + γ・δd
これがあったところで、普通の人は何もできない。
ところが、YMB25pro4MIのツール群を使えば、(溶媒のCAS#と誘電率は持っているとして)1分もあれば検証できる。オリジナルでは範囲を限定していたのに、いつの間にか式だけが一人歩きしていることもある。
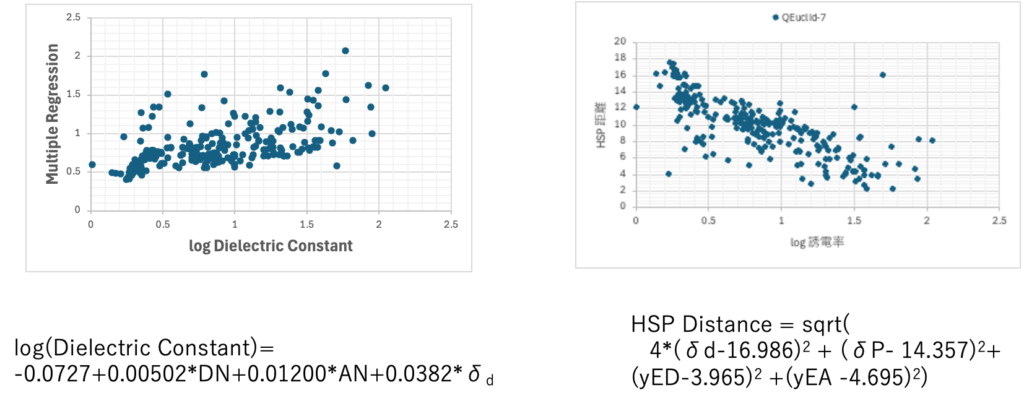
瞬間で P0 +α・DN + β・AN + γ・δdの係数を決めることができる。HSP距離法との違いを考える事ができる。(18)式はリニアなのでDNもANも大きくなればなるほど誘電率は大きくなる。HSPの距離は、dD=16.986,dP=14.357, yED=3.965, yEA=4.695の時ゼロになる。つまり誘電率は最大になる。その点からの距離だけで誘電率が決まると言っている。4つのパラメータのどの方向へ遠ざかるかは関係ない。解釈は随分違う。
すると次から次へと疑問が湧いてくる。どんなものが合わないでそれはなぜか? 考える。なんとタイパの悪い人生だ。
結局、暇な隠遁生活を送らないためには、タイパの悪い、「AIに解析しろって命令する人がいないようなつまらない事」に興味を持つしかないわけか。自信あるな。忘れ去られたような古い本にはいくらでもネタが転がっている。
グラフをじーっと見れば、拡張HSP2を使ったものの方がちょっと精度が高そうにも見える。でも35年の時差を考えると、これではダメだ。
そこで、やることは上に外れるもの、下に外れるものを抽出してその理由を考える。
例えば、25度で気体のものは合っていないものが多い。カルボン酸化合物はダイマーを作っているのだろう。合わない。カーボネート系のものもあまり良くない。パラメータが悪いのか。足りないものを補正項として式に入れる。
誘電率とは何か?
その本質を自分が納得できるのが楽しいのでやっている。
ニッチな領域に勝手に興味を持つAIが開発され、ブラックボックスで答え出してくれても嬉しくも何ともない。自分が知らないだけで、誘電率なんてとっくの昔に解決済みかもしれないし。
日本人の研究者はタイパが重要なので、こんなページには目もくれなくてよい。
隠遁してから暇つぶしに読んでくれれば良い。
隠遁生活悪くはないが、論文とかが取れないのだけは痛い。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください
