2025.2.1
情報化学+教育 > YMB Pro for MI >
注意:HSPiPに搭載の機能ではありません
遷移エネルギーET(30)
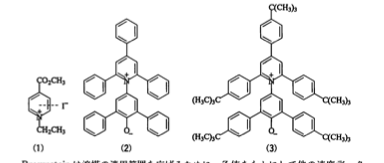
極性分子の電荷移動型の電子遷移に伴う紫外可視吸収帯は溶媒極性に大きく依存している。遷移エネルギーET(30)が様々な溶媒について決定されている。

溶媒(262種)のCAS番号とET(30)の値は準備してあるとする。
HSP距離の33式
次世代HSP2では、分散項の分割、dH項の分割を行い、HSP距離の式が33種類になってしまった。どの式が物性を一番良く記述できているかわからないので、全部の式を作り結果を解釈していく。ここでは特にdHの分割が問題になる。
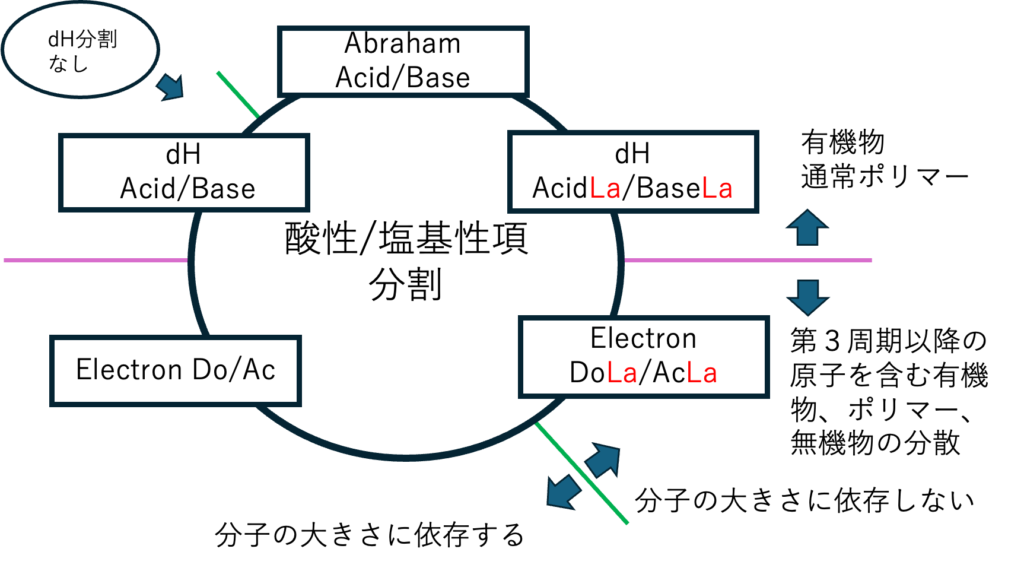
教科書(有機化学反応と溶媒)に書いてあった、ET(30)とアクセプター数の関係から考えて、yED, yEAを使った分割がとても有効でないか?と期待できる。

New Sphere計算用のデータフォーマット作成
CAS番号(もしくは溶媒のSMILES構造式)とET(30)の値があれば、HSP距離の33式はすぐに求まる。ビデオを参照して欲しい。
HSP距離の式
HSP距離の式というのは、たとえば溶媒のHSPとポリマーのHSPがあったときに、そのHSPがどのくらい離れているのかを計算する式のことだ。一番基本の距離の式はHansen先生の作られた、次式になる。
HSP distance =(4.0*(dD1-dD2)2+(dP1-dP2)2+(dH1-dH2)2)0.5
詳細は距離の詳細を参照して欲しい
ここではET(30)は実数なので、HSP距離とET(30)が最も高い相関になるようにSphereの中心を求める。
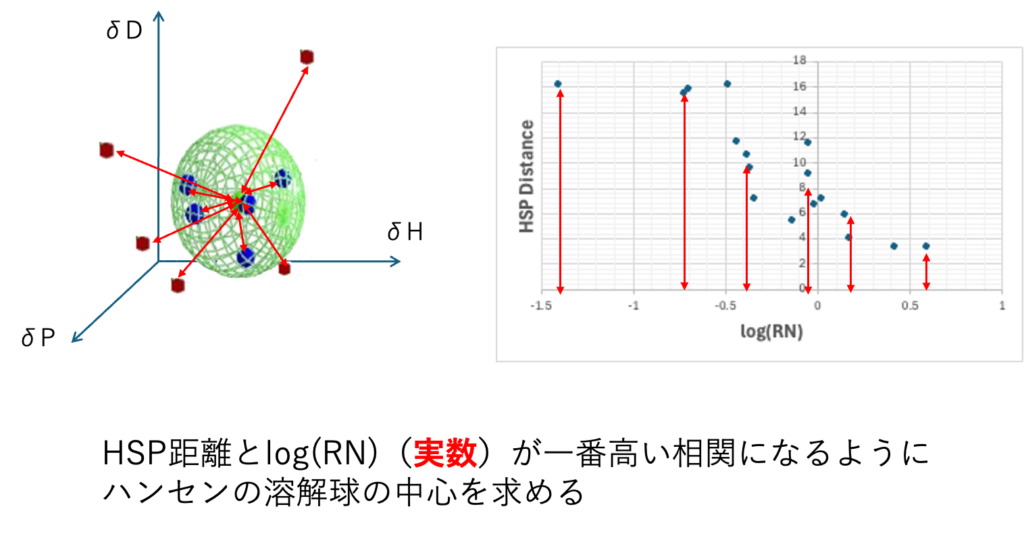
33式の結果を見る
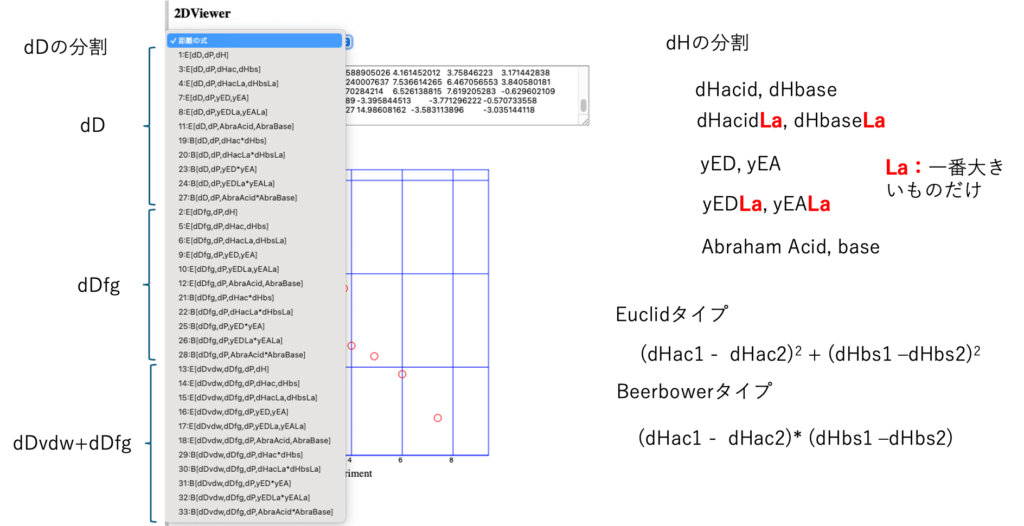
YMB25Pro4MIの中にもビュアーがあるので直ぐに式のパーフォマンスをチェックできる。
HSPが進歩しない理由
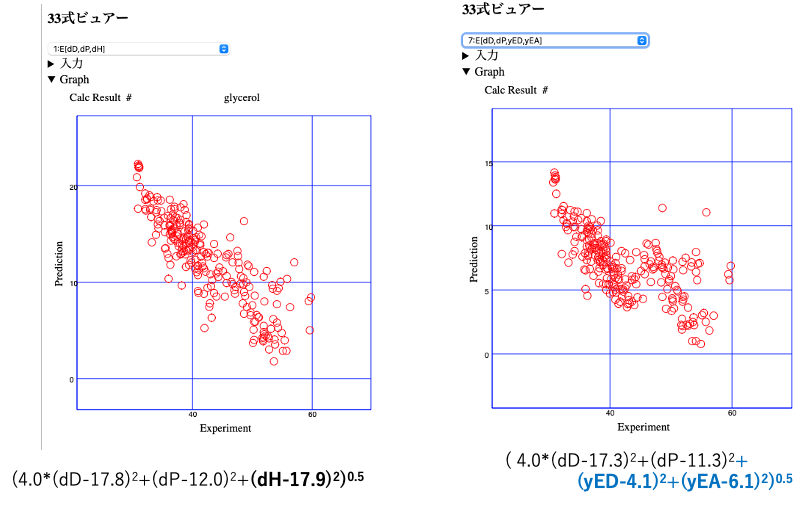
HSPをHansen先生と開発している自分が言うのは何だが、クラッシクHSPはパーフォーマンスが高すぎる。左図で見るようにHSP距離が短くなるとET(30)が大きくなる。
HSPが[dD, dP, dH]=[17.8, 12.0, 17.9]の時にHSP距離が0になる。つまりその時が最大のET(30)となる。yED, yEAを導入した右図では相関係数はとても悪くなる。
一生懸命考えても、やればやるほど悪くなる。
自分も、ET(30)とアクセプター数(AN)のグラフを見ていなかったら、ここで止めていたかもしれない。
合わないものを何故合わないのか考えるクセをつける
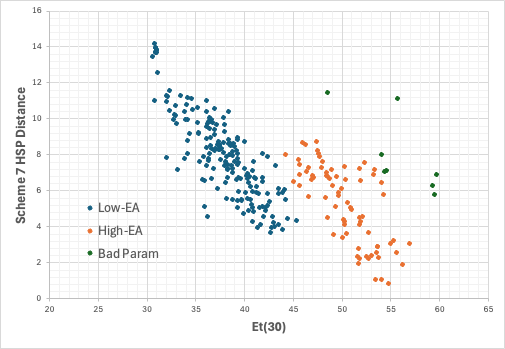
この場合は、簡単だ、ET(30)が45以上(オレンジ)と以下(ブルー)で、機構が異なるのだ。幾つかの大きく外れるものは、私の作ったyED/yEA推算ルーチンの出来が悪いからだろう。
誘電率の高い溶媒も、極性が高い
溶解度パラメータにドナー数、アクセプター数を導入。僕が初めてでは無かった。残念!でも書いたように、誘電率という物性はHSP距離であらわすときにyED/yEAを導入するとパーフォマンスは高くなる。
また、普通に考えて、極性が高い物質は誘電率も高い。(この時もクラッシクHansenのパーフォマンスの高さが光るが)
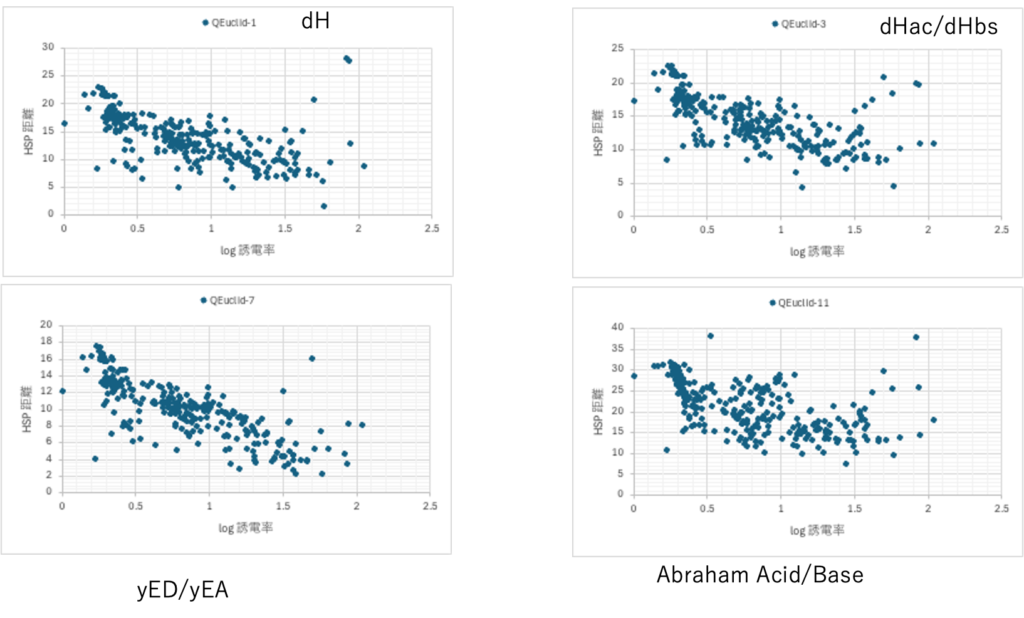
誘電率とET(30)は相関がある。
溶媒分子の双極性と分極率による溶媒極性は,静電相互作用の理論に基 づいて比誘電率を用いて Kirkwoodパラメーター(ε-1)I(2ε+1) で表現することもできる。
これを知っていれば、すぐに検証することができる。
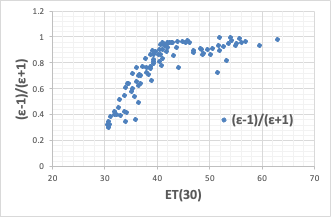
すると、すぐに不思議なことに気づくだろう。ET(30)が45以上と以下で、機構が異なるのだ。
ET(30)=45のギャップ
何故こんなところにギャップがあるのだろうか?
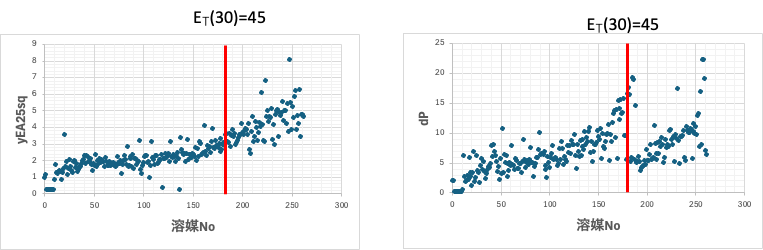
データをよく見るとすぐに気がつく。溶媒をET(30)でソートしてNew Sphereの項目とグラフを作ってみる。ET(30)=45の溶媒は180番目の溶媒だ。それ以上の溶媒はyEAが大きく、dPが小さいという特徴を持つ。具体的にはアルコールやフェノール系の化合物だ。
元々、HSPの理論の中でも、dPとdHの成分わけは難しい。アルコール基は水素結合もするし、分極もしている。しかし、どちらかというと水素結合の方に大きな値が割り振られdPが小さくなる。
極性という1つのパラメータで見てしまうと、クラッシクHansenの距離の式が精度良く見える。dPとdHは整合性あるようにパラメータ化されているので、矛盾なく見える。
ET(30)はyEAと単相関が高い
その事実を無視してクラッシク・ハンセンを使い続けるのも一つの方法であろう。
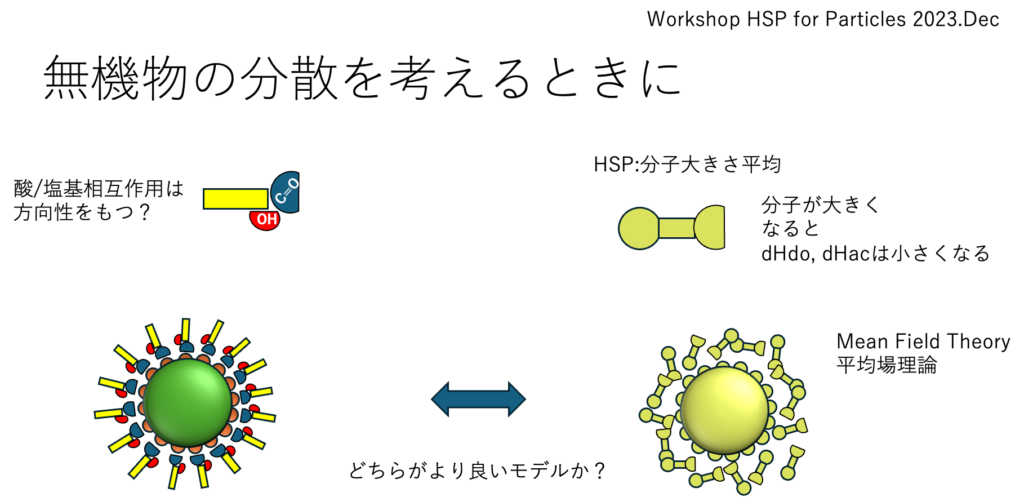
しかし、無機物の分散安定性などになってくると、どうしてもdHだけでは精度は出なくなる。ET(30)の本質が溶質に対するドナー/アクセプター数であるなら、最適設計は距離の式にyED, yEAを含むものを使い、場合分けをした方が理解しやすくなる。
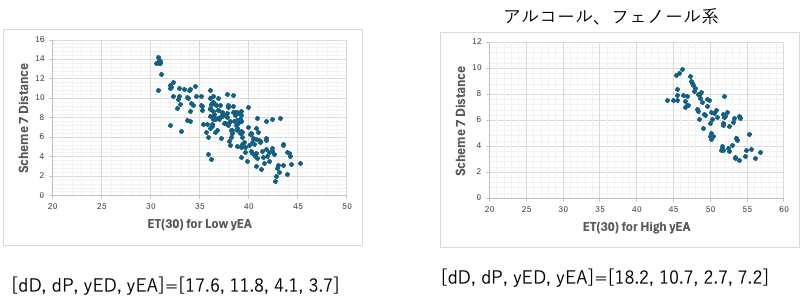
クラシック・ハンセンは性能が高すぎる
YMB25Pro4MIを使えば簡単に試せるので、トライして欲しい。いい暇つぶしになる。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください
