薬でもハートでも、溶かすには距離が大事なのは説明するまでもない。
問題は、重要度が軸によって異なる事だ。
他の2つが一致していても、残りの1つが何倍も重要だったりする。
ハンセンの溶解度パラメータは、[δD,δP,δH]をベクトルと捉え、ハンセン空間での距離を計算して、距離の短いもの同志は溶解しやすいと考える。
ここで敢えて、”ハンセン空間”と断ったのは、ユークリッド空間では無いからだ。
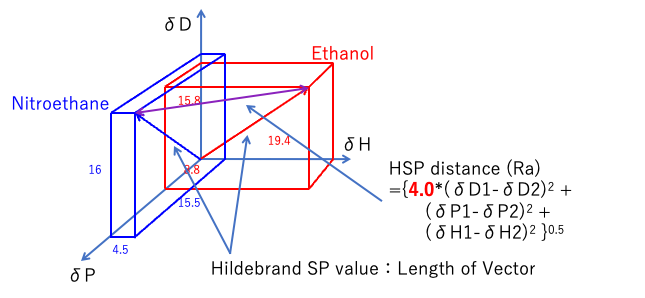
HSP ディスタンスの分散項(δD)の差分の前に4.0という係数がついている。
そこで、ハンセン空間では、δD軸に関して２倍引き伸ばしてあげないと、ハンセンの溶解球は、球ではなく、ラクビーボールになってしまう。
このことは、実務的にはHSPはとても役に立つが、訳のわからないパラメータ4.0が入っているので理論的には意味がないと言われてもいた。
この問題に関しては、2017年のHSP50周年、記念講演会で新しいHSP2を使えば解決することを示した。近いうちに発表になるHSPiP ver.6では重要なポイントになるので、敢えて説明しておこう。
ハンセン溶解度パラメータ、分散項(δD)に関する考察
希ガスが非常に弱い分子間力なのは誰も異存ないだろう。
その分子量と沸点の関係を見てみよう。
ヘリウム、ネオン、アルゴン…と分子量が大きくなるにつれ沸点が高くなる。
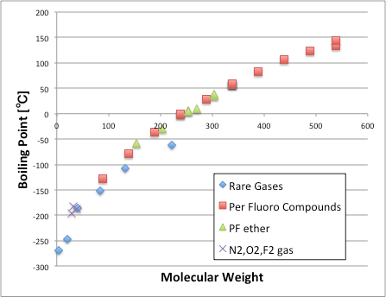
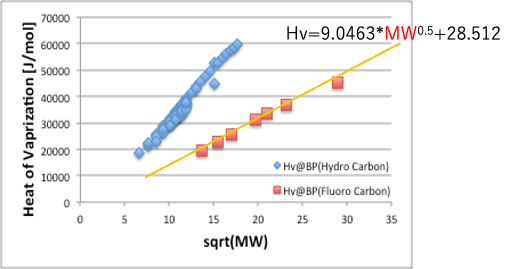
そこに、パーフルオロ化合物やパーフルオロ・エーテル化合物の分子量と沸点を加えると、これも曲線に乗るのがわかる。
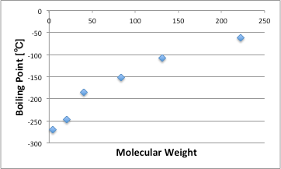
つまり、化合物には、分子量（分子体積）だけに依存した、ベースになる分子間力があるということだ。
分子量を持てば必ず持つ、弱いVDWの力になる。
この結果から考えると、PTFEというフッ素ポリマーは、（他のものと分子間相互作用を持たない）希ガスのポリマーとも考える事ができる。
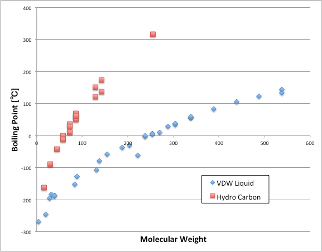
そこに、鎖状の炭化水素をプロットすると赤四角で示したようになる。
ハンセンの溶解度パラメータの理論では、鎖状の炭化水素はδD(分散項)だけをもち、δP、δHはゼロになる。
しかし、この炭化水素のδD(分散項)は、希ガスなどの分子量による弱いVDWの力よりも、さらに大きな分子間力を持つ。（そこで、その力を断ち切るのに高い温度が必要になる。）
溶解度パラメータの定義式は次のようなる。
δ=((Hv – RT)/Volume)0.5 Hv: Heat of Vaporization,蒸発潜熱
Troutonの通則というのがあり、沸点における蒸発潜熱を沸点で割った値は正則溶液では一定になる。そこで、軸変換をしてみる。
縦軸にHvを取り、横軸を分子量のルートを取ると、フッ素化合物の曲線は直線になる。
そこで、ベース部分のHvは,
9.0463*MW0.5+28.512と表す事ができる。
この蒸発潜熱を分子体積で割ったもののルート取れば、弱いVDWに相当する溶解度パラメータを得る事ができる。
それを、δDvdwと定義する。
δDvdw=((9.0463*MW0.5+28.512)/(MVol))0.5
どんな分子でも、分子量(MW)は簡単に手に入るし、分子体積(MVol)はY-MBで簡単に計算できる。
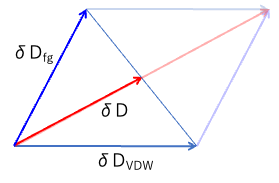
炭化水素は、δDvdwに加えて、分子の持つ官能基に依存する分子間力を持つと考える。その分の溶解度パラメータをδDfgと定義する。
δD2 = δDvdw2 + δDfg2
δDは元々のHSPなのでデータがある。 δDvdwは簡単に計算できるので、δDfgも簡単に求まる。
HSP50では距離の式として次のものを提案した。
Distance1967={4.0*(δD1-δD2)2 +(δP1-δP2)2 +(δH1-δH2)2}0.5
Distance2017 = {(δDvdw1-δDvdw2)2 +(δDfg1-δDfg2)2 +(δP1-δP2)2 +(δH1-δH2)2}0.5
これまでの、4.0は無くなり、4次元のユークリッド距離になった。
つまり、本来のδDは菱形の対角線にならなくてはいけないのに、その半分にしてしまったので、倍してあげないと合わない。（ルートの中で扱う時には4倍）
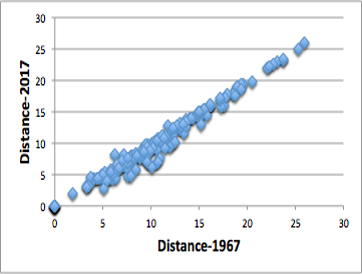
この新しい距離を用いて、HSPiPの中にあるポリマーの溶解性のデータに適用してみた。
ハンセン先生が1967年に提案した式にはマジックナンバー4.0が必要で、polymer 88 solvent同士の距離を全て計算した。
それと今回作成した式で計算した距離を比較すると、右図のように非常に高い相関を示した。
この距離の式を使って、例題を解析したときに、間違ってハンセンの溶解球の外にでた良溶媒と、間違ってハンセンの溶解球の中に入った貧溶媒の数を調べたところ、全ての系で改善されている事がわかった。
この結果から、δDを分割して新しい距離の式を使わない理由は、ただ一つになる。
つまり、4次元データをビジュアルに表現する方法がないという事だった。
これに関して、主成分解析(PCA)で次元縮退させた例をブログにあげてあるので、そちらも参照していただきたい。
やっと、このパラメータ利用の目処がついたので、ver. 6に向けて開発を急ごうと思う。
ちなみに、この新しいセットを用いた時の最も大事な成果を紹介しておこう。
シリコーンオイルも、フッ素オイルもとても疎水的で、水には溶解しない。
そして、HSPはとても似ているのに、溶けあわない。
| Name | dD | dP | dH | 1967 Distance |
| Dimethoxydimethylsilane | 12.82 | 3.19 | 4.03 | 2.04 |
| 1,1,2,2,2-Pentafluoroethyl 2,2,3,3,3-pentafluoropropyl ether | 12 | 3.59 | 2.88 |
| dDvdw | dDfg | dP | dH | 2017 Distance |
| 9.88 | 8.16 | 3.19 | 4.03 | 8.5 |
| 12 | 0.02 | 3.59 | 2.88 |
ところが、新しい距離の式で見ると、8.5となり、なぜ溶け合わないか明確に判るだろう。