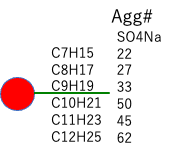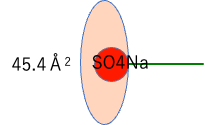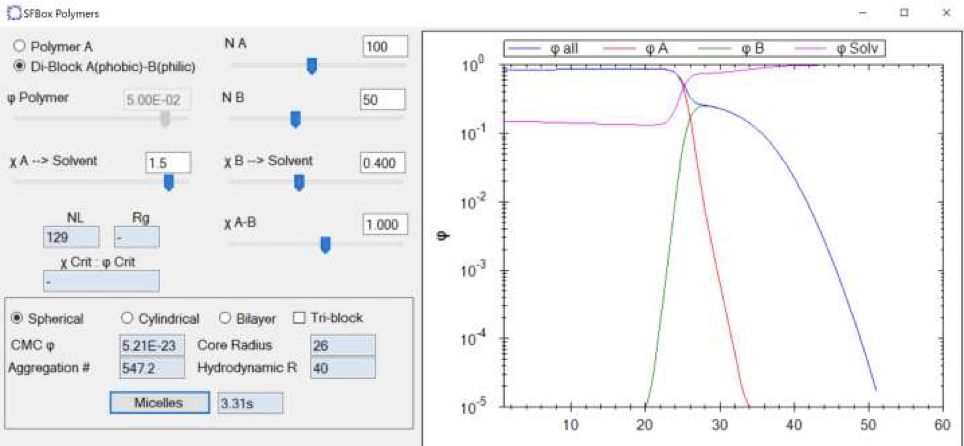
HSPiPのSFBoxを使うと、「臨界ミセル濃度（CMC）、Aggregation #、Core Radius、およびHydrodynamic Radiusの計算値も得られる。」とe-Bookにあった。
SFBoxは確かHSPiP ver.5.3から導入された機能だ。真面目に翻訳して初めて気がついた。CMCとAggregation#が分かると色々なことができる。
そこで、界面活性剤に関して既にわかっていることをまとめておこう。
その前に次の公式は思い出しておこう。
球の体積の公式は？
球の表面積の公式は？
球の体積(V)が与えられたとき球の表面積の値は？
球の断面積の値は？
臨界ミセル濃度(CMC)
界面活性剤がある濃度(CMC)を超えるとミセルを形成し始める。
そして様々な物性はCMCを境に急激に変わる。
界面活性剤が何個集まってミセルを作るか？ をAggregation #という。
ここまでは、教科書にも書いてあるだろう。
まず、Aggregation #を考えてみよう。
それでは、このミセルが球であったとして球の体積を求めてみよう。
どうやれば球の体積がわかるだろうか？
そう、界面活性剤の疎水基の体積とAggregation #を掛け算してあげれば良い。
疎水基の体積は、とりあえず、対応するSmilesの構造式からHSPiPのY-MBを使って分子体積を計算する。
| Mol Volume | SO4Na-Agg# | Micelle-Volume | Micelle-radius | Micelle-Surface | Surface/Agg# | |
| C6H13 | 120.0 | 17 | 2040.3 | 7.869 | 777.8 | 45.6 |
| C7H15 | 136.7 | 22 | ||||
| C8H17 | 153.4 | 27 | ||||
| C9H19 | 169.2 | 33 | ||||
| C10H21 | 185.9 | 50 | ||||
| C11H23 | 202.6 | 45 | ||||
| C12H25 | 219.3 | 62 |
疎水基が大きくなるにつれ、Aggregation #も大きくなる。その二つをかけたミセル体積も大きくなるだろう。
その時のミセルの半径も簡単に求まるだろう。
(4/3)Πr3が分子体積になるので、
r=power(Vol*3/(4*3.14),(1/3))
になる。
半径がrの球の表面積は4Πr2なので、rが求まっていれば、ミセルの表面積もすぐに計算できる。
そのミセルの表面積をAggregation #で割ってあげれば、一つの親水基がカバーする面積が求まる。
さー、テーブルを埋めてみよう。
親水基のしめる表面積は45.4Å2となり、疎水場の大きさとは全く関係ない一定の値になる。
つまり塩に水和している水の量は一定ということだ。
親水基の部分を変えるとどうなるだろうか？ Aggregation #は次のテーブルのようになる。
| Volume | COONa | COOK | COOCs | SO4Na | SO3Na | NH3Cl | NMe3Cl | NMe3Br | PyrBr | PyrCl | |
| C7H15 | 136.7 | 20 | 22 | ||||||||
| C8H17 | 153.4 | 27 | 28 | 20 | |||||||
| C9H19 | 169.2 | 33 | |||||||||
| C10H21 | 185.9 | 50 | 51 | 39 | |||||||
| C11H23 | 202.6 | 50 | 45 | 42 | |||||||
| C12H25 | 219.3 | 50 | 62 | 54 | 56 | 47 | 54 | 46 | 19 | ||
| C13H27 | 235.1 | ||||||||||
| C14H29 | 251.8 | 80 | 55 | 66 | 72 | 79 | |||||
| C15H31 | 268.5 | ||||||||||
| C16H33 | 285.2 | 100 | 81 | 92 | |||||||
| C12Ph | 281.6 | 17 | |||||||||
| C6H13 | 120.0 | 17 | 3 |
各親水基の水和面積を求めてみよう。
| 水和面積 | |
| SO4Na | 45.4 |
| COOK | |
| COONa | |
| SO3Na | |
| NH3Cl | |
| NM23Cl | |
| NMe3Br | |
| Pyridine-Br | |
| Pyridine-Cl | 65.9 |
| Phenyl-SO3Na | 80.8 |
計算してみれば、簡単にわかるように、SO4NaからPyridine-Brまで、親水基の構造が変わっても、水和面積はほぼ同じになる。
その水和面積になるように、水分子を配置させると、14個ぐらいの水が配位して居る事になる。
HSPiP中のY-MBの作者としては「Y-MBでは界面活性剤のように塩が含まれるとHSPが計算できない」と言われるのは心外だ。そこの部分は水と同じHSPとしておいても全く問題ない。せいぜい、水和面積に依存した値にしておけば良い。
そして、疎水場のHSPと体積から、界面活性剤の平均値としてのHSPは計算で出せる。
しかし、そんな平均値など全く意味を持たないので、出力しないだけだ。
ここの部分の面白さは、水の電子供与性、電子受容性だ。それが水和構造を作るのであって、HSPが作るのでは無い。
もう一つ非常に重要な点は、芳香族についた塩(Phenyl-SO3Na)は非常に大きな水和面積を持つという事だ。この事は、芳香属性のアルコール（フェノール）についても言えることだ。
（ポリオキシエチレン：PEG系の界面活性剤も同じように解析するととても面白い。リクエストが多ければ公開しよう。）
それでは、フェノールにはどのくらい束縛水があるのだろうか？
これについては、後半で解析する。
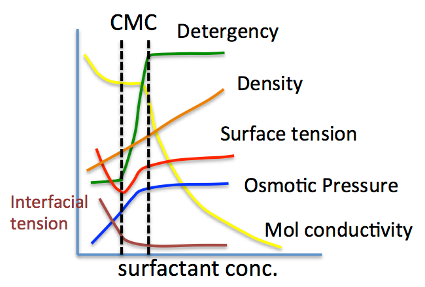
それでは、CMC(臨界ミセル濃度）とは何か？を考えてみよう。
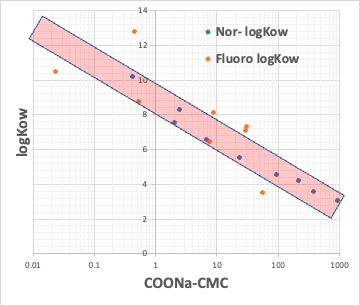
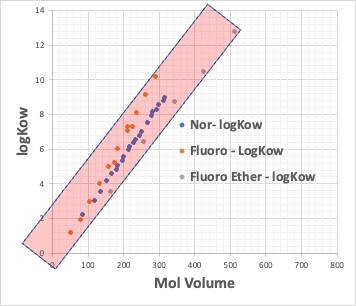
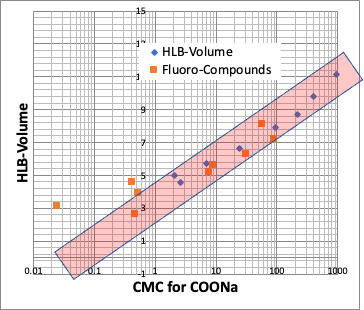
例えば、カルボン酸のNa塩のCMCとカルボン酸の疎水場(COONaを取り去った残りの部分）のlogKow(オクタノール/水分配比率）とをプロットしてみる。
Kow=17.4とするとオクタノール層に17.4, 水へ1、分配する
疎水場が普通の炭化水素と、フッ素化合物のものがあるが、どちらであっても、CMCとlogKowは逆相関がある。
logKowとMol Volumeには正の相関があることが知られている。
そこで、CMCに対して、疎水場の分子体積をプロットすると、フッ素系、炭化水素系に関わらず非常に高い逆相関が得られる。
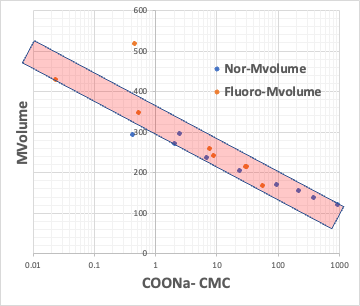
CMCが小さいということは、低い濃度でミセルを作る。それは疎水場の分子体積が大きい時に起こる事になる。
つまり、疎水場の分子体積が決まれば、CMCが決まり、Aggregation #も決まる事を意味している。
芳香属性で無い親水基なら、構造が変わっても関係ない。
ちなみに、界面活性剤の評価値として、HLB(Hydrophile-Lipophile Balance)というものがある。著名なのは、Griffin法で、次のように計算する。
HLB=20*親水部の式量の総和/分子量
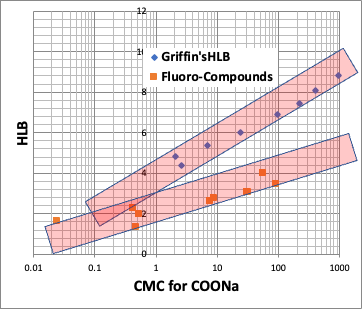
このHLBとCMCは高い相関があることが知られている。
フッ素系の界面活性剤は分子量が大きくなるので、炭化水素系とは異なる線になる。
分子体積ベースにすると、炭化水素系、フッ素系の違いは無くなる。
そこで、pirikaが提案する、HLBは次のようになる。
pirika HLB = 20*親水部の式量の総和/疎水場の分子体積
つまり、HLBも疎水場の分子体積だけで決まると言える。
このように、界面活性剤はHSPiPに搭載されているY-MBを使って疎水場の分子体積を計算すれば、CMC, Aggregation #, HLBが計算できてしまう。
SFBoxとの整合性が非常に楽しみなところだ。
それでは、さらに疎水性相互作用を考えてみよう。
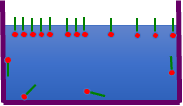
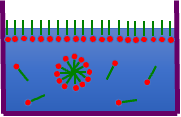
親水性の部位と疎水性の部位を持つ分子は、疎水性の部分が疎水性相互作用で集合してミセルを作ると教科書は教えてくれる。
しかし、データ集を見ていると、炭素鎖が６以下ではミセルを作ることは無いようだ。
（枝分かれのない）アルキル基が（６つぐらいある）と鎖と鎖が揃いはじめ、多くの界面活性剤はC12以上で疎水性相互作用が顕著になると言われている。
その疎水性相互作用はどのように定量化できるのだろうか？
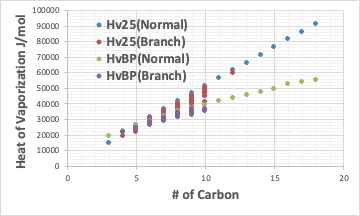
直鎖状の炭化水素の炭素数に対して蒸発潜熱をプロットするとこのようになる。
25℃での蒸発潜熱と沸点での蒸発潜熱を示してある。基本的には25℃での蒸発潜熱は（沸点が25℃以下でなければ）沸点の蒸発潜熱より大きい。それは25℃から沸点まで温めるエネルギーが余分に必要だからだ。
非常に興味深いのは、Hv25(Normal)は炭素数に関してほぼ直線になることだ。
HvBP(Normal)は炭素数が大きくなると蒸発潜熱の増加率が減ってくるので曲線になる。
また、同じ単素数であっても枝分かれが増えて、分子が球形になってくると蒸発潜熱は小さくなる。
そのような場合には、Troutonの通則（沸点に対して沸点における蒸発潜熱をプロットすると直線になる）に従いプロットしてみるのが有効だ。
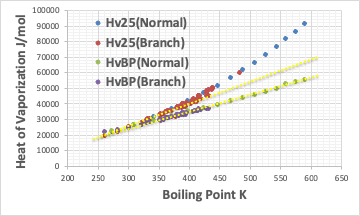
このように、HvBPは直鎖であろうと分岐型であろうと一つの直線に乗る。
それに対して、Hv25はC9以下では直線に乗るが、それ以上では明らかな屈曲点が存在する。これが、疎水性相互作用を打ち壊すのに必要な余分なエネルギーになる。
それが短いアルキル鎖ではほとんどないため、ミセルを作れないと考えられる。
このように、本来は疎水場の分子体積だけではなく、分子の形状（分岐）なども考慮に入れなくてはならないが、疎水性相互作用がある程度わかってくる。
後半に続く。