2時間の映画を10分に縮めて見るような忙しい学生が、片手間でできるもんではないので、やめとけって授業では話した。
そのうちAIがプログラムなんて書いてくれるだろうし。
グローバルで活躍するには、英語が必須って、大学院の授業を英語にしたのはいいけど、先生も学生も慣れないで、授業としてはどんどんレベルが下がる。
その間に、DEEP Lとかが進歩して、グローバル化に英語なんて必要ないって言う時代が来てしまう。
プログラムだってそうなるだろう。
プログラミング教育で一番大事なのは、
アルゴリズムに則った考え方ができるか?
例外を網羅できるか?
だと思う。
細かいテクニックは、その都度やっていけば良い。
アルゴリズムって何だろう?
整理された考え方って事だろうか。
何故、整理しなくてはならないのかというと、AIはとてつもなく馬鹿で、常識が無いからだ。
人間が人間に考え方を伝えるなら、常識を働かせることを期待する。
研究室で、先生が修士の学生に指示するようなものだ。
だけど、学部生なら少ない常識に合わせて濃い説明をしなければ同じ動作は期待できない。
AI相手では幼稚園生にも満たない常識しかないと言う前提に立つ必要がある。
例えば化合物の分子量を計算することを考えてみよう。
C6H14と言う化合物があったとする。
高校生ぐらいの化学の常識があれば、周期律表から原子量を持ってきて、
MW(C6H14) = 12*C#+1*H#
と計算できる。
ところが、AIにはそもそも原子とか重さとか言う常識が無い。そこで、C(炭素)はCl(塩素)、Ca(カルシュウム)、Cr(クロム), Co(コバルト), Cu(銅)Cd, Cs,Ceとは違うことを教えなくてはならない。
具体的にCの右隣に何かアルファベットの小文字があるかどうかを調べさせなくてはならない。
数字だったら炭素と判断していいかと言うと、Cが1の時は記載しない(CH4, CHCl2Fみたいな)事を考慮しなければならない。
Hについても、Hg(水銀)やHf, Hoと区別しなくてはならない。
そうなってくると、うん、化学の知識なんて、いちいちアルゴリズム作るよりも、ビッグデータを与えて、幼稚園生から大学院生レベルになるまでディープ・ラーニングさせてしまえって事になる。
これがどんどん進んでくれば、英語をDEEP Lに任せるように、化学や薬学もAIに任せる時代がそのうち来るだろう。
だから、忙しい学生がわざわざ、プログラミングなんて学ぶ必要はない。
もし、
アルゴリズムに則った考え方ができるか?
例外を網羅できるか?
に興味があるなら、プログラミングを学ぶのはとても意味があると思う。
例えば、分子体積を計算することを考えよう。
分子量は、そのグラム数取ってくれば1モルの数の分子になる。そこで、密度(g/cm3)がわかれば、MW(g/mol)/密度(g/cm3)=分子体積(cm3/mol)が得られる。
それでは、密度のBig DataがあればDeep Learningで分子体積の計算機が作れるか?を考えてみよう。
例えば、炭素と水素だけからできている化合物がある。
鎖状炭化水素、環状炭化水素、オレフィン、環状オレフィン、芳香族化合物が相当する。
この分子体積の一覧を作って、分子の原子団との関係を調べる。
(どんな原子団があったら、分子体積がどうなるか?)
最近のExcelに搭載されている回帰計算では変数の数は13個ぐらいまでしか計算できない。しかし、RやPythonが使えるなら簡単に回帰係数が求まるだろう。
そうすれば分子量の時と同じように、計算式は求まる。
分子体積= 28.65*CH3# + 15.84*CH2# + 3.29*CH# -13.51*C# ・・・・・
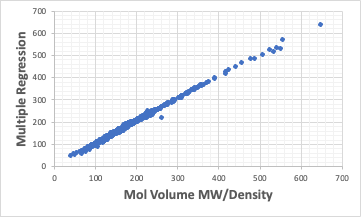
一点だけおかしなデータがあるが、分子が決まり、それを原子団に分割すれば分子体積は計算できる事になる。
この程度で十分なら、プログラミングなど学ぶ必要はない。ソフトの使い方を学ぶだけで良い。
プログラミングを学んで欲しいのは、ここで疑問を持つ人材だ。
分子量は良い。1つの原子に1つの原子量だから、回帰式に疑問はない。
分子体積は、回帰係数が1つに決まるものなのだろうか?
例えば、4級炭素の係数が、-13.51になっている。
4級炭素と言えども、原子の大きさは持っているわけで、それが分子の中に入ったときに体積が小さくなるとはどういう意味を持つのか?
欲しいのは、数理統計的結果では無い。回帰の係数を負にしないと言う制限をかけた時には、各原子団の係数は幾つになって、トータルの精度はどのくらい悪くなるのか?
その精度の低下が軽微なら、回帰の係数は負にしたくないと言うケースは化学的にはある。
例えば、溶解度パラメータは分子体積あたりの蒸発潜熱のルートで計算される。
原子団あたりの溶解度パラメータを求める時には負の値は困る。
先程の分子体積の計算結果を一部拡大すると次のようになる。
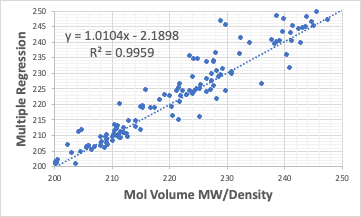
同じものをGROVE法で計算してみる。(GROVE法はpirika研究会に参加していた学生にプログラムの勉強で作ってもらったものだ)
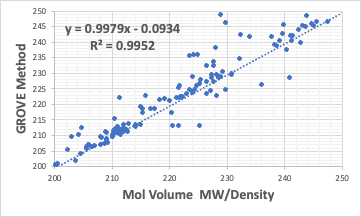
R2は通常の重回帰計算と比べ、0.9959から0.9952 へ低下する。
しかし、Xの係数は1.0104から0.9979、切片は-2.1898から-0.0934とY=Xに近くなる。
またグラフを見ると、通常の重回帰はY=Xの上下に均等にバラけている。GROVE法では線に乗るものはなるべく線に乗り、離れるものは大きく離れている(あまりはっきりしないかもしれないが)。どのようにプログラミングしたらそのような結果が得られるだろうか?
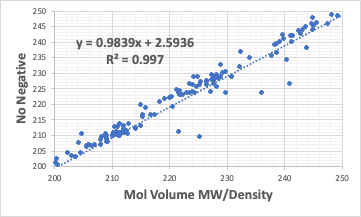
さらに係数を負にしないと言う制限をつけると上図のようになる。
R2は0.997ととても高くなり、平均的に良くあっている。
(どうプログラミングしたらそんな制限が実現できるだろうか?)
すると、前のやり方で大きくずれるのは、4級炭素に負の値が割り振られていたからとも考えられる。
このように、自分でプログラムが書けると言うことは、様々な可能性に対して定量的に検証を行うことが可能になると言うことだ。
結果として、各原子団に割り振られる係数は、すぐに5-6種類ぐらいに増える。
そうした値をベースに色々思考する。
通常の重回帰ソフトを使うなら、いつも答えは一つだ。(逆行列法を使うなら)Rを使おうがPythonを使おうが同じ答えしか出せない。
分子体積では、大して面白いことへは繋がらないが、薬や触媒の設計になると、原子団の見方が決定的に変わったりする。
AIのBig Data解析は中身がBlack Boxになる。
でも、自分が感じる何故だろうに対して自分で解析ツールを作って計算してみれば何故そうなったかが分かってくる。(なぜ4級炭素に負を割り振らないと上のような結果になるか考えて見れば良い練習になる)
この、係数を負にしないという機能は、まだGROVEには搭載されていない。
もし、そんな事をきっちりやりたい学生がpirika研究会に入ってきたら、その辺りからリスタートかな。
ちなみに分子体積に関しては、数理統計の研究者には多分わからない難しい事が含まれる。
例えば分子が大きくなると、融点が室温以上になる。つまり25度での密度は固体の密度になる。しかし温度を上げれば、密度自体小さくなる。どうしよう?
逆に25度で気体の化合物の密度はどうだろう?
圧力をかければ液化できる。そうした25度の液体密度はそのまま使って良いだろうか?
特に気体に関してはBig Dataなんて無い。小さい分子だけだ。
こうした化学者の知見を入れ込んだBlack Boxでない予測式をAIアシストで作成すれば、「普通の人は、僕らが作ったAIシステムのユーザーに徹すれば良い」=「プログラミングなんて必要ない」が実証されるのだろう。
プログラマーが寝ないで頑張っている間に、ゆっくりと映画を2時間観ながら待っていれば良い。
