引火性ありなし、アレルギー性あるなしなどの○✖️判定は、ロジスティック回帰を使うと教科書にはある。pirika研究会で開発した解析ツールMIRAIを使った場合の○✖️判定結果の見方を解説しておこう。
MIRAI(Multiple Index Regression for AI)のP(Power)を使うかG(Gauss)を使うか悩むが、取り敢えずMIRAI-Gを使う。
解析したデータセットは、179個の○✖️がある。(107個のX、72個の◯)
説明変数は87種類。
こうした説明変数の種類が多く、データ数に限りがあるようなケースに、MIRAIは効果を発揮する。
まず行うことは説明変数をグループ分けすることだ。
例えばアルカリ金属は全部一つのグループに入れる。とか。アルコール類は1級、2級、3級、フェノール性のOHを1つのグループに入れてしまう。とか。
ここでは、14グループに分けた。
目的変数は、◯は1、Xは0として、解析をスタートする。
5万サイクルぐらい計算すると結果が落ち着く。
するとMIRAIは、ある説明変数の組みに対して、予測値を返す。
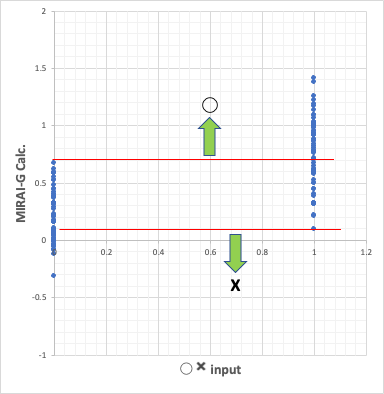
X(0)のもののMIRAI-Gの計算値は、-0.31〜0.67になる。
そこで、MIRAI-Gの計算値が0.67以上なら結果は◯(1)であると予測される。(緑の上矢印)
72個の◯の内、57%が0.67以上になる。
◯(1)のもののMIRAI-Gの計算値は、0.093〜1.41になる。
そこで、MIRAI-Gの計算値が0.093以下なら結果はX(0)であると予測される。(緑の下矢印)
107個のXの内、51%が0.093以下になる。
赤線の間の、0.093〜0.67の間に計算値が来た時には判定がつかなくなる。
そういう見方では半分ぐらいは判定がつかなくなる。
そこで、0.5で区切ってみる。
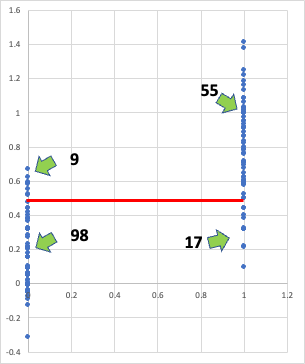
計算値が0.5を超えた場合、55*100/(55+9)で86%の確率で◯(1)であると予測される。
計算値が0.5以下の場合、98*100/(98+17)で85%の確率でX(0)であると予測される。
計算値が0.5以上か以下かで85%程度の確率で○✖️判定できるので、それなりに良い判定になる。
何故、曖昧領域が出てくるか?
今回解析したデータのうち、MIRAI-Gの計算値が全く同じ(説明変数が全く同じ、ほぼ同じ)であるにも関わらず、結果が◯の場合とXの場合があるので、85%以上の確率にはならない。
昔行った計算で、引火点のあるなしを予測した時に実際にあったことだが。
燃えないとされていたものが、実際には比重が重く、着火源のあたりに居ないため燃えないと判定されていたことがある。攪拌したら燃えたのだ。
安定性の○✖️判定で、◯だと判定されたものが、実は見えない内部で分離していた事もあるかもしれない。
同じ実験を5回再現実験して、◯が3回、Xが2回であるかもしれない。(元々不安定)
Aさんがやった実験とBさんがやった実験で結果が異なるのはよくある事だ。
特に化学の領域は、不確定要素が多いので、100%はほぼあり得ない。
そこで、不確定なら不確定と言ってくれないと困る。
ニューラルネットワークのDeep Learningだかで、ブラックボックスだけど○✖️判定を教師データに従って100%分離したなんていうのは全く意味のない結果だ。
MIRAI-Gの計算値が小さいのに、◯であったものはよく調べてみるべきだ。
もしかしたら、◯だと思っていたものが入力ミスかもしれない。
しかし、何か不明の原因で(例えば攪拌とか)◯になる要因があって、それを見つけたら大発見につながる可能性もある。
逆に計算値が大きいのにXであったものもよく調べてみると良い。
いわゆる計算機屋はこうした結果だけをとやかくいう事はできる。
でも、化学者だけが、解釈を与えることができる。
現象をよく知っている者の方が圧倒的に強い。
計算をやりっぱなしにしない事だ。
