2021.5.5
情報化学+教育 > 情報化学 > 原子団寄与法の基礎
ここでは、一番単純で、昔からある原子団寄与法という物性推算法と、その根底にある重回帰法をまとめ直しておきます。
それは、今(2021.4-)、MAGICIAN養成講座に参加している学生と、新しい解析用のツール、GROVEを作成しているからです。
GROVEというのは Gene-based Regression Offering Valuable Equations の略です。
学生に教える都合上、この連休は重回帰法の基礎を勉強し直すことにしました。
種本は、
エンジニアのための実践データ解析、藤井宏行著、東京化学同人
です。
最近、データ・サイエンスとかが大流行りした(もう過去形??)こともあり、化学系の学生も慣れない統計を勉強しなければならなくなりました。そして、どこもかしこも、[あやめの分類(./SOMdoubutu.html)と、有機物の水への溶解をPLSなどを使って解析を繰り返しています。
この種本は、東京化学同人が出しているだけあって、化学系のデータを解析することに主眼が置かれています。
まだ、浮かれていない2005年に出版されているのも良いです。(古すぎず、新し過ぎず、入手可能)
題材は何にしようか悩んだ末、敢えて現在の潮流に逆行して原子団寄与法を取り上げます。
最近のMaterials Informatics(MI)などでは、[RDkit(https://www.pirika.com/Education/JP/ChemoInfo/RDKit.html)を使ってフィンガー・プリント(指紋)を吐き出させて解析とか、分子軌道計算(MO計算)結果を使って解析などが多いです。
原子団寄与法を取り上げるのは、現在でも広く使われている、Joback法物性推算を開発したJoback先生と私は友人で、今でも色々議論しながら研究を進めている関係だからです。もう一つには、私は元々は実験系の高分子合成の研究者でした。そうした私がカルフォニア工科大学のGoddard教授の元に留学して、計算機科学を学んだ際に、Directorの一人に「高分子物性に興味があるなら、Van Krevelenの Properties of Polymersの重回帰解析は、しっかり学ぶように」と指導されたからです。
それでは、まずJoback法による有機化合物の沸点推算に関して考えてみましょう。
有機化合物の沸点推算
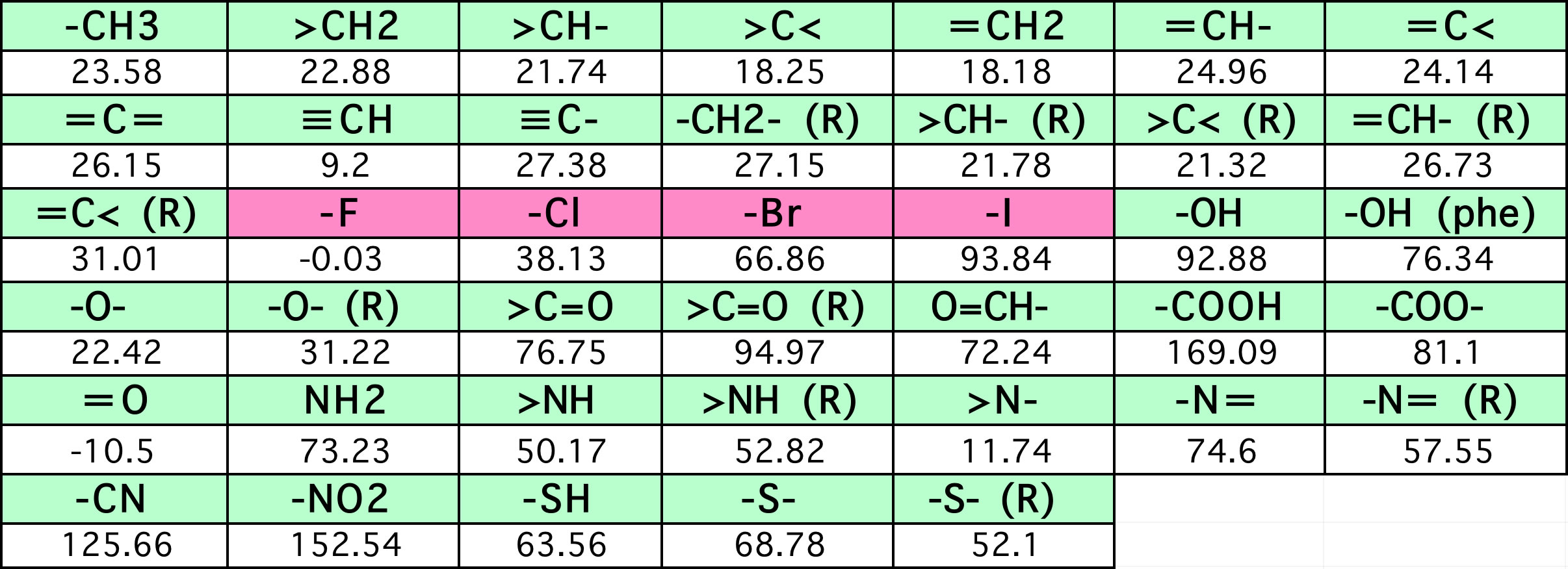
沸点=198.2+Σ(原子団の数 * 表中の係数)
Joback先生は沸点推算用の原子団パラメータを1984年にMITの学位論文に発表されています。 分子中の原子団を数え上げれば、その分子の沸点を予測することができます。
Joback先生との蛇足(▶︎をクリックして開く)
Joaback先生と奥様を我が家に招待して、明け方まで議論したことがあります。実はJoaback先生と私は同じ年でした。学生時代に使っていた大型コンピュータは、パンチカードでプログラムを読み込ませるものだったのも同じです。
その頃から急速にパーソナル・コンピュータが実用的になって、私も先生も夢中になったのも同じでした。
Joback先生は、コンピュータを利用して、系統的に解析を行った研究者として著名となったのですが、それ以前にもLydersen先生は1955年に原子団寄与法の係数を発表されています。
1955年では流石にコンピュータの利用は無理でしたでしょう。では、どうやって係数を定めていったのでしょうか?
次のテーブルをExcelなどの表計算ソフトに貼り付けておきましょう。
これは、原子団としては、CH3, CH2, CH, Cだけから構成されている飽和炭化水素の沸点を集めたものです。このテーブルを用いて原子団の沸点に及ぼす寄与率を求める練習をしてみましょう。
テーブル中の最初の19個の化合物は枝分かれのない炭化水素になります。
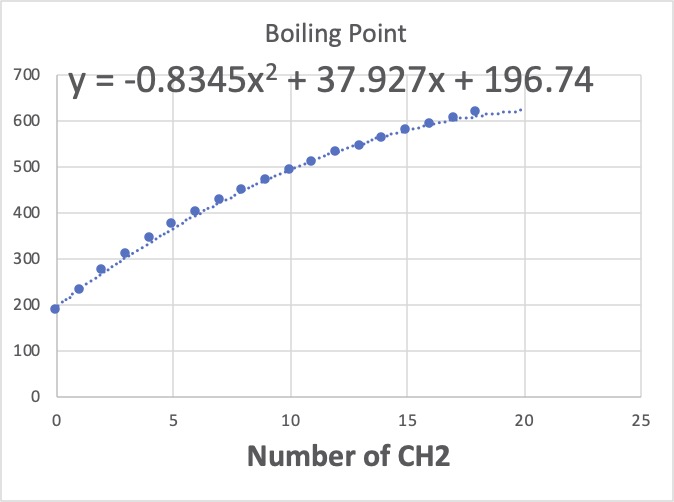
これらは、CH, Cの数は皆同じで0になります。CH3は全て2個で、CH2の数だけが変わります。これをグラフに描いてみましょう。
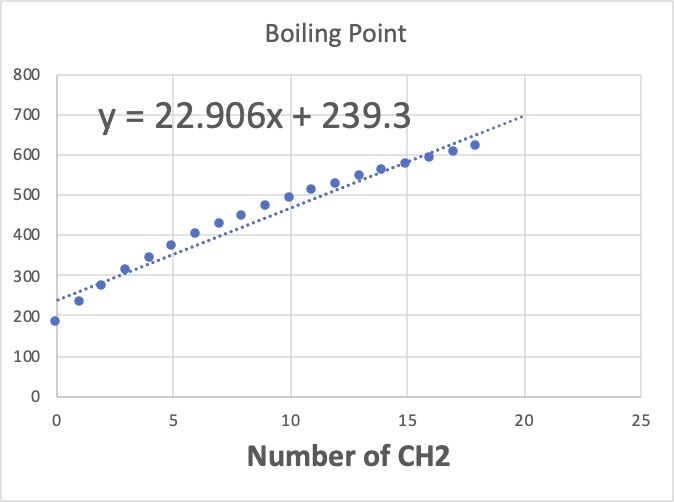
このグラフの意味することは、CH2が1つ増えると、沸点は平均22.906℃高くなることを示しています。Jobackの加算値は22.88なのでとても近いですね。
Jobackの定数項は198.2なのが、ここでは239.3なので悪くありません。
コンピュータのないLydersenの時代には、このようにグラフなどを利用しながら、寄与率を決定して行ったのでしょう。
では、次に、実際にCH3の加算値を決定してみましょう。
例えば、エタン(CH3-CH3)はCH3のみからできているので、CH3の加算値を決定することができます。
すると、すぐにでも困ったことになります。
定数項が0であれば、CH3の係数は沸点(184.5K)を2で割った値になります。
しかし、定数項がいくつであっても、(184.5-定数項)/2がCH3の寄与率になるので1つには定まりません。
2行目から19行目のノルマル・アルカンではCH2の係数は22.906と求まっていますが、CH3の数はどれも2なのでCH3の係数はやはり不定になってしまいます。
そこで、CH3の数が増減して、他のCH2, CH, Cの数が一定の化合物を探してみます。
| CH3 | CH2 | CH | C | Boiling Point (K) |
|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 184.5 |
| 3 | 0 | 1 | 0 | 261.3 |
| 4 | 0 | 2 | 0 | 331.2 |
| 5 | 0 | 3 | 0 | 386.6 |
すると、当たり前のことですが、CH3の数が変わる(大きくなる)ということは、手が3本、4本の原子団が増えるということで、独立にCH3だけの数を変えることはできません。
そこで、Lydersenの時代の頃の原子団寄与法ではCH3の加算値はCH2と同じにしているものが多いのです。UNIFACなどの気液平衡(VLE)などの計算用のソフトでもCH3をCH2として扱います。
もう少し、進歩した形として、連立方程式にして解く事も可能は可能です。
| CH3 | CH2 | CH | C | Boiling Point (K) |
|---|---|---|---|---|
| 4 | 3 | 0 | 1 | 380 |
| 3 | 3 | 1 | 0 | 366.6 |
| – | – | – | – | – |
| 6 | 0 | 2 | 1 | 414.7 |
ただし、61個の連立方程式をコンピュータもなく解くのは難しかったのではないかと思います。
今の時代であれば、原子団の数を増やしたところで、非常に簡単に重回帰計算を行うことが可能です。
しかし、そんな時代だからこそ寄与率の意味を良く考え直す必要があります。
グラフ法で解こうが、重回帰法で解こうが、データの母集団をどう捉えるのか?
それが、最も重要なポイントです。
逆にいえば、ビッグデータ、ビッグデータとやたらとデータを増やすことが正しいことなのか考え直す必要があるということです。
CH2が8以下ではCH2の加算値は、32.408と先ほどと比べると大きな値になります。
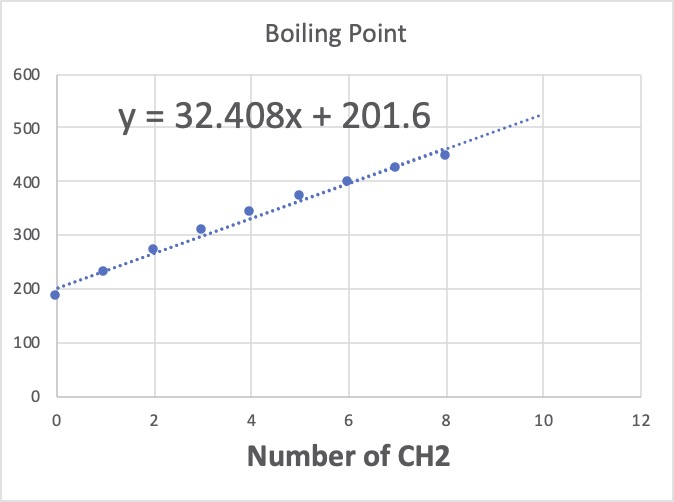
逆にCH2を10以上にすると、加算値は15.842と小さくなります。
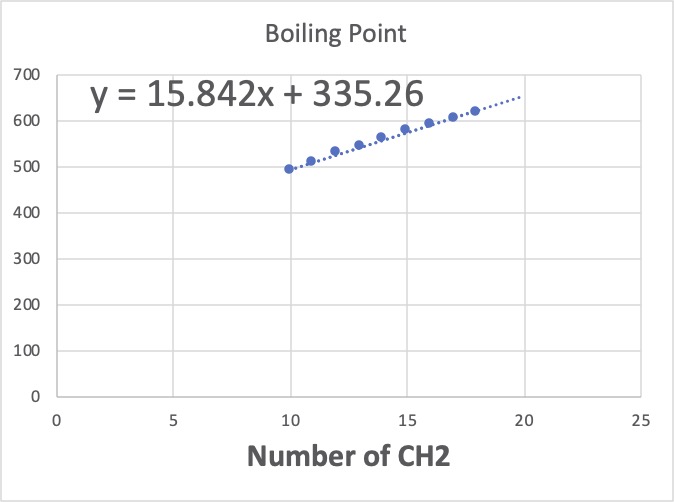
自分が使いたい領域がどこかで範囲を考えるものであって、オールマイティーなモデルを探すのは、ごく一部の研究者に任せれば良いということです。
多項式の非線形性を導入すれば、領域に関係なくモデルが成立しそうに誘惑されるかもしれません。
それがノルマル・アルカンだけではなく、枝分かれ構造を持つもの、芳香族が入ったもの、酸素や窒素などのヘテロ原子が入った場合、ハロゲンが入った場合などでも、ここで定めた非線形式が成立する保証は全くありません。
それら複雑な非線形性が組み合わさって、中身がブラックボックスになってしまったAIを作りたいのであれば、インスタグラムにある35億枚の写真を学習させるように、PubChemにある化合物の精度の高い沸点のデータを集めて解析すればいいでしょう。何億個集まるでしょうか?
重回帰法の問題の第一は、母集団によって解析結果が大きく変わるということです。
まず最初の教訓は、「先に母集団を決めよう」です。
グリーン・ソルベントの物性推算
グリーン・ソルベントと呼ぶ場合には、どうも2つの意味が混じっているような気がします。
一つには、今まで人間が食料として摂取してきた化合物は毒性が低い。つまり、エステル、カルボン酸、アルコール、エーテル結合だけからなる溶媒などは、一般に毒性が低く、微生物によって分解されやすく環境負荷が低いのでグリーン・ソルベントと呼ばれてもいます。
グリーン・ソルベントの毒性などに関しては、pirikaのこちらにまとめてあります(/GreenSolvents.html)。
本来の、グリーン・ソルベントの意味では、持続可能性も含め、例えば大豆油のように石油に頼らず入手できて、環境負荷が低いものを指すべきかもしれません。
(かと言って、肥料や農薬はどうなのでしょう?)
そうした生物由来の原料は混合物であることが多いので、物性推算には馴染みません。
そこで、ここでの母集団としては、環境負荷が低い単一構造のグリーン・ソルベントを母集団にすることにします。
ネットを検索すると様々なカタログがダウンロードできます。
そのカタログに載っているデータを母集団にすることにします。
私が、この連休で重回帰法を勉強し直している理由の一つが共線性の問題です。
入力された「説明変数間に高い相関がある場合には共線性の問題」が出てくるので、重回帰法では解けない。その場合には主成分分析やPLS解析を行うと教科書は教えてくれます。
ところが、どうも、自作(とは言っても、昔の書籍に記載のプログラムを書き直したもの)のものではあまり明確な不具合は無かったのでうまく説明できませんでした。
新しく、学生の作っているGROVE解析ソフトで、顕著にこの問題が出てきて、初めて「共線性はやばい」と実感したので書き留めておきましょう。
重回帰法における共線性の問題
「説明変数間に高い相関がある場合には共線性の問題」が出てくると言われても、化学者にはなかなか意味不明でしょう。
まず、もう少し具体的な例題で共線性の概念を把握してみましょう。
先程の例題であった沸点のテーブルです。
| CH3 | CH2 | CH | C | Boiling Point (K) |
|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 184.5 |
| 3 | 0 | 1 | 0 | 261.3 |
| 4 | 0 | 2 | 0 | 331.2 |
| 5 | 0 | 3 | 0 | 386.6 |
これを連立方程式にすると、値が皆ゼロのCH2列、4級炭素Cの列は除いて次のようになります。
2*a1+0*a3 +const. =184.5
3*a1+1*a3 +const. =261.3
4*a1+2*a3 +const. =331.2
5*a1+3*a3 +const. =386.6変数が2個で式が4つあるので連立方程式は解けそうな気がします。
しかし、後ろの式から前の式を引き算すると出てくる式は、a1+a3の式だけで、変数消去はできません。
右辺の定数は異なりますが、平均値の67.4としても、a1=67.4 – a3となり、値は不定になります。
a1+a3 =76.8
a1+a3 =69.9
a1+a3 =55.4当たり前のことですが、逆行列も求まらないので、通常の重回帰を行うと、a1+a3=67.4となる無数の組み合わせの中のどれか適当な値が入ってきます。
イメージ的に言うと次のようになります。
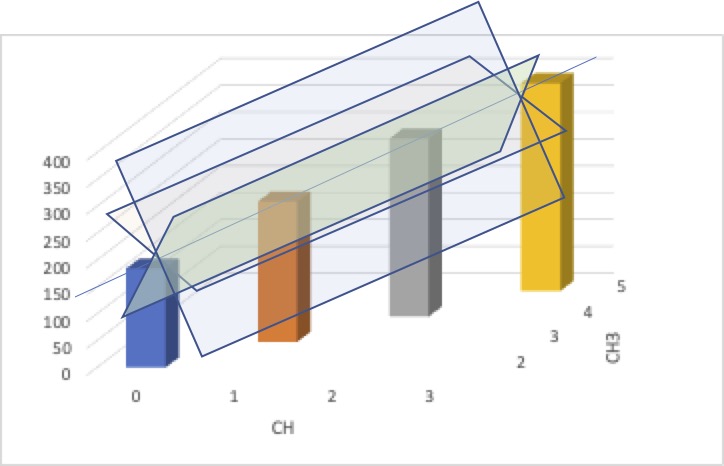
この4つのデータポイントは、縦軸を沸点、横軸をCH3の数、CHの数として3次元プロットすると、ほぼ直線に載ってしまうと言うことです。
そして、そして、その直線を含む平面は幾つでも仮定できてしまい、一つには決まらないと言うのが共線性の問題です。
主成分分析を使うと共線性の問題が回避できることがあるのは、通常のX,Y,Z,・・・軸から新たな軸を作成するときに、今回の軸を採用すれば、軸を一つ削減した効果となるからです。
説明変数間に極めて高い相関がある。
ある2つの説明変数の線形和が、別の線形和とほぼ等しい。
共線性となる条件ですが、「極めて」とか「ほぼ」とかなんとも曖昧な表現になります。
まー、難しいことは兎も角、中学で習った変数消去法で連立方程式を解こうとしたり、こまめにグラフを書いてみることです。
重回帰係数がおかしな値になったり、解が不安定になったりする場合には共線性を疑う。
これが2番目の教訓です。
何故、すぐにGreen Solvents(GS)の物性推算に行かなかったかというと、GSの官能基をJOBACK法の原子団に分割して物性推算を行なったところ、共線性の問題で値が不安定になる原子団が3組あったからです。
特に思いもよらなかったのが、CH=_RとC=_Rが共線関係にあったことです。
(_Rは環の中にある原子団です。)
データの中にあったものは、全てCH=C_Rの形で環の中に入っていて、CH=CH_Rとか、C=C_Rの形のものはひとつもなかったので共線関係になっていました。
通常の広い範囲の溶媒群では原子団の多様性が確保されていたものが、GSと狭い範囲に限られてしまったためにこの問題が出てきたということです。
それでは、GSに戻り、物性を予測してみましょう。 ここでの原子団は共線性を回避するために合体させた原子団としています。
オリジナルのデータは私が集められるだけ集めたものです。
最初の教訓:母集団の問題もあります。
自分が興味のある領域の溶媒を強化したり、データが正しいか確認したり、化合物の追加、削除、データの改訂などを行いましょう。
場合によっては原子団の削除や追加も必要かもしれません。
こうしたことを行えば、狭い領域かもしれませんが、グリーン・ソルベントに関して、自分だけを助けてくれるようなAIアシストを構築することができます。
次のグリーン・ソルベントの物性データと構造識別子をコピーして表計算ソフトにペーストしておきましょう。
原子団寄与法の係数は物性値ごとに決定することになります。
Excelに搭載されている回帰計算では変数は16個までなので、今回のサイズになると計算できません。授業で使っているYSBや新開発のGROVEなどを使って解析していくことになります。(もちろんPythonやRを使った解析でも良いですが。)
まず、水への溶解度から始めましょう。
全ての溶媒について、水への溶解度のデータがあるわけでは無いので、データのあるものでテーブルを作ります。
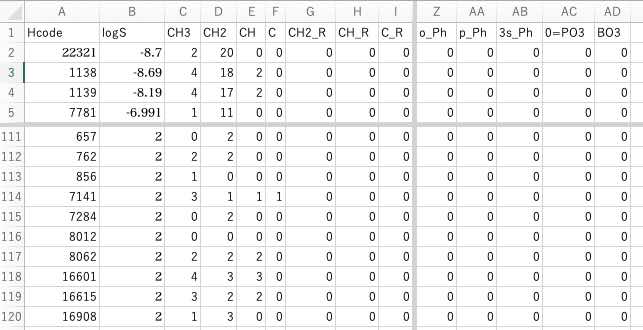
2列目に目的変数のlogS(log Solubility to water g/100g Water)を入れます。
C列目からどの原子団を何個持っているかの列になります。
このテーブルを重回帰解析すると、各原子団の係数は次のように求まります。
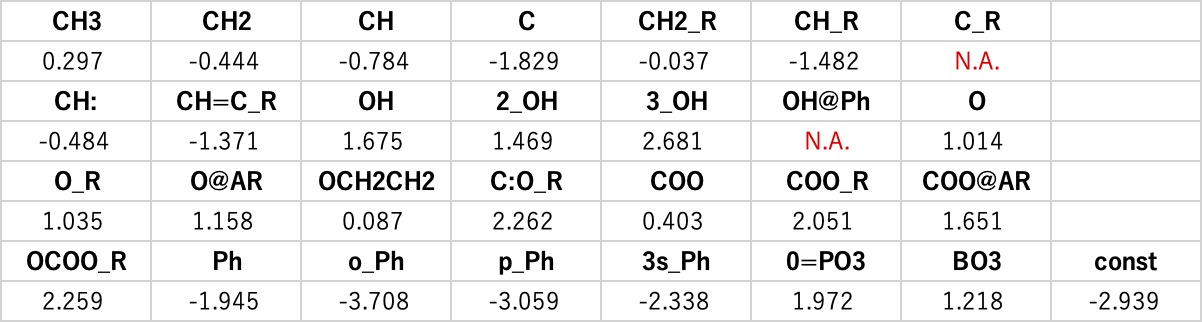
C_R(環状の4級炭素、OH@Ph(芳香属性の水酸基)はデータが一つもないので係数が求まりません。
それ以外の原子団は表のように係数が求まります。
試したことは無いので、確実なことは言えませんが、どんな統計解析用ソフトで計算しても同じ結果が得られると思います。
それは、どの方法を用いたところで、ソフトの内部的には行列の逆行列を求めて係数を決定するので、Rを使おうがPythonを使おうが答えは変わり得ないということです。
この係数が得られてしまえば、計算したい化合物、例えばCH3OCH2CH3であればCH3が2個、CH2が1個、Oが1つなので各係数と個数を掛け合わせ定数を足せば水への溶解度を予測することができます。
1級水酸基、2級水酸基、3級水酸基で水への溶解性がどう変わるか考えることができます。
このように重回帰法で求めた原子団の寄与率は「一つに決まり、意味合いもはっきりしている」と思いがちですが、それは間違いです。
母集団が異なれば、原子団の寄与率は異なります。
しかし同じ母集団であっても、解析目的によって原子団の寄与率は異なって当然なのです。
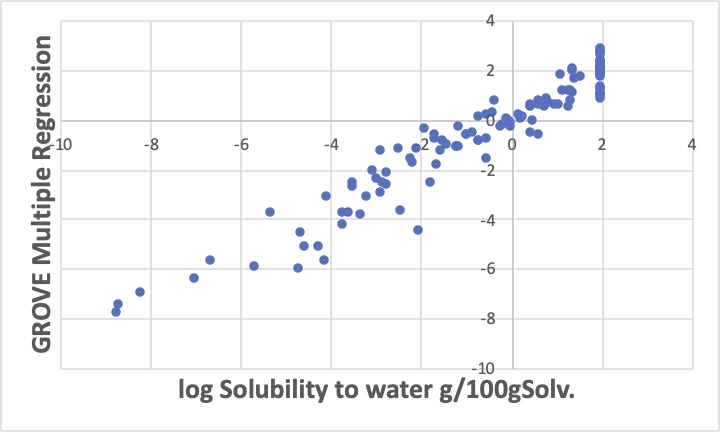
先程のテーブルの係数を用いて重回帰計算をするとこのような結果になります。そこで、水への溶解度のデータのないグリーン・ソルベントがあった時に、その原子団の数を数えて重回帰係数を掛け合わせれば、このグラフ程度の誤差は出てしまうかもしれませんが、予測値が求まります。
ところがGROVE解析ツールでオプションを変えて重回帰係数を求めると、母集団は同じでも全く異なった結果になります。
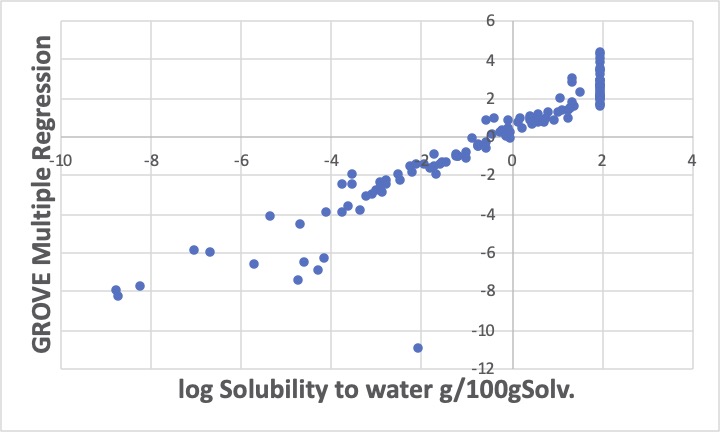
log水への溶解度が-2ぐらいの化合物の予測値が-10以下と非常に大きく外れます。
前のグラフでは、悪めではありますが、他にも悪いものが多く、データのクレンジング](https://www.pirika.com/Education/JP/MAGICIAN/Examples/No5.html)(悪いデータを削ぎ落とす)は難しいです。
log水への溶解度が2と言うことは、水100gに溶質が100g溶けると言うことで、通常100g/100gで自由混合ということで実験は打ち切られます。最初のグラフで、log水への溶解度が2あたりの予測値は0.78から2.78になります。gに直すと、6g/100g水から602g/100g水です。本来自由混合である化合物が6gしか水に溶けないと予測されてしまいます。
従って本来、自由混合なので親水性と判断される原子団の重回帰係数が過小評価されていることになります。
2番目のグラフではそれが大きく修正されているのがおわかりいただけるでしょう。
全体的にY=Xの直線上によく乗っていますが、外れるものは大きく外れています。
従って、重回帰係数は一義的に決まるものはなく、解析目的に合わせて変わっていくものです。
GROVE解析ツールで四種類のオプションを試したところ、テーブルにある原子団の重回帰係数は次のようにばらけたものになります。(値が1違うということは、logでは10倍違うことに注意してください。)
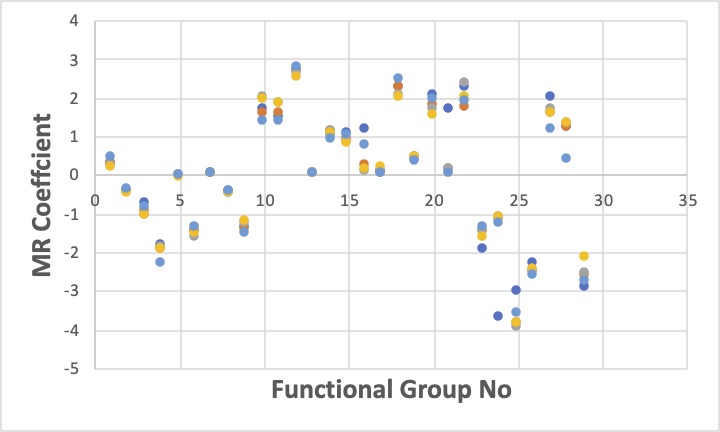
どれが、正しいのでは無く、目的によって使い分けて行くモノなのです。
通常の重回帰ソフトしか選択肢が無いのであれば、迷う必要は無いのでシンプルな生き方が可能です。
教訓:目的に合わせた重回帰係数を使う。
次に原子団寄与法の問題点は、「定義されていない原子団は使えない」に尽きます。
この水への溶解度のデータの場合、C_R(環状の4級炭素)、OH@Ph(芳香属性の水酸基)はデータが一つもないので係数が求まりません。
そのような時どうするか?
例えば、C_R(環状の4級炭素)を鎖状の4級炭素のパラメータを代用する、芳香属性の水酸基のパラメータを1級OH基のパラメータで代用する事などはよく行います。また、ひたすらデータを探すのも大事です。グリーン・ソルベントだけから探すからデータが無いので、パラメータを決めるためだけにグリーンでなくてもテーブルに溶媒を継ぎ足すのは悪く無いでしょう。
ここでは、別のやり方で欠損データを補ってみましょう。
重回帰法である目的変数を予測する時には、目的変数と(複数の)説明変数のテーブルを用意します。原子団寄与法では原子団がいくつあるかを説明変数に使いました。
説明変数として、RDKitの吐き出すトポロジカルな識別子を使う、分子軌道計算して計算値を識別子に使うでも構わないのです。
先程のGSのテーブルの原子団の後ろにRDKitの厳選識別子を加えてあります。
この識別子を用いて水への溶解度を予測する式を作成します。
するとRDKitで計算できる化合物(Smilesの分子構造式から計算する)であればどんな化合物でも予測値を得ることができます。
つまり、C_R(環状の4級炭素)、OH@Ph(芳香属性の水酸基)を持つ化合物であっても、予測値は得ることができてしまいます。その予測値を使って、C_R(環状の4級炭素)、OH@Ph(芳香属性の水酸基)の重回帰係数を仮決めしておきます。何時かデータ値が出た時に差し替えれば良いのです。(とは言っても中々やらない怠惰な性格ですが。。。)
早速やってみましょう。
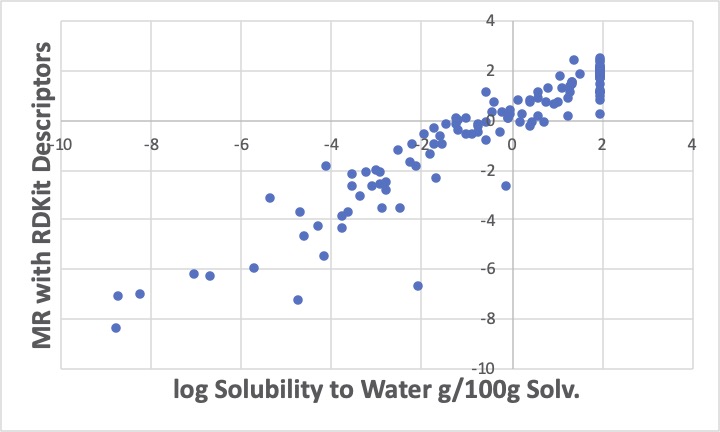
原子団のテールをRDKitの識別子に変更して重回帰計算をすると、余り上手く推算できていないようです。RDKitの出力した識別子を厳選したと言いましたが、他の識別子を使う、Finger Printを全部使いPLSやPCA解析するのも一つの手かもしれませんが、ここではGROVE解析ツールを使って解析してみます。
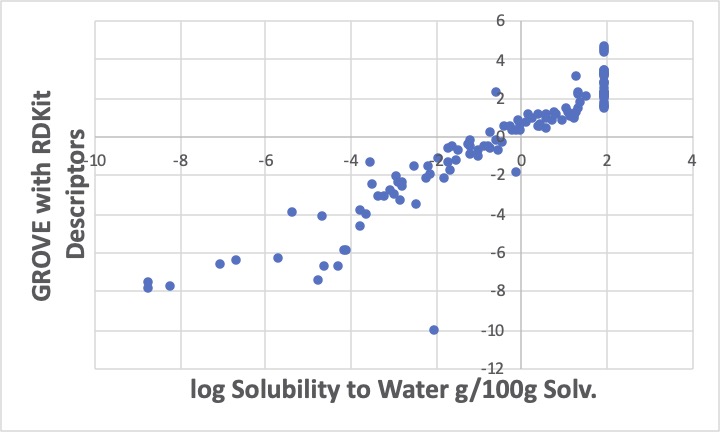
このように、logSが-2から0の間に3つほど大きく外れる化合物があり、Y=Xの線から遊離してきます。その分、他のデータはY=Xの線に乗ってきます。
この重回帰係数を用いて、C_R(環状の4級炭素)、OH@Ph(芳香属性の水酸基)を持つ化合物の水への溶解度を予測し、原子団ベースで、また、GROVE解析すれば、未知のパラメータを決定できるということです。
本来の
データを見直す。
データを増やす。
努力をするのはもちろんですが、GROVE解析ツールなどを利用すると、そうした作業も非常に効率化できるのは確かなようです。
最後に蛇足ですが、通常の重回帰法で計算される重回帰係数とGROVEのものと比較すると次のようになります。
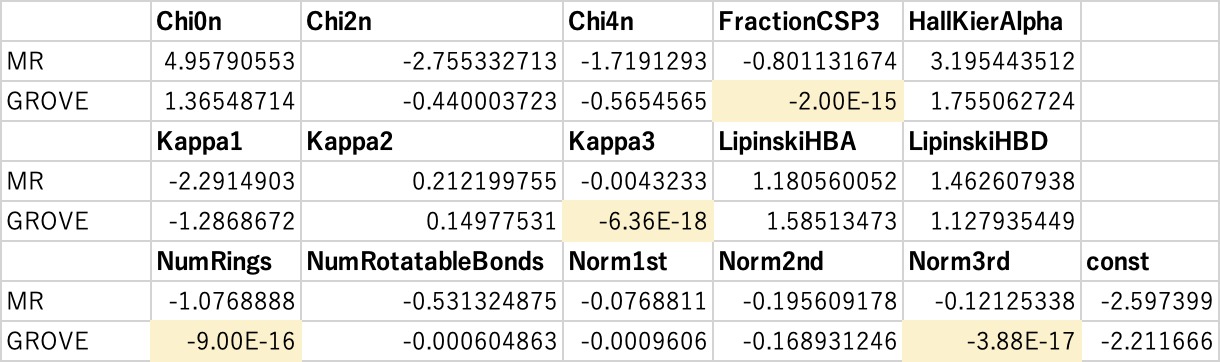
GROVE解析では、役に立っていない識別子の係数をどんどんゼロにしてしまいます。
この場合だと、4つの識別子はいらないと判断されました。
データのクレンジングができ、かつ、識別子の刈り込みもできる解析ツールとして、GROVEは面白いツールに育ちつつあります。
情報化学+教育 > 情報化学 > 原子団寄与法の基礎
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
