2014.08.01
情報化学+教育 > 情報化学 > ハロメタンのNMR・ケミカルシフト
Pirikaのサイトでは、重回帰(MR)法、ニューラルネットワーク(NN)法、遺伝的アルゴリズム(GA)法を使ったデータ解析法を自作のプログラムを作成して利用しています。
それらがどういう意味を持つのかハロメタンの13C-NMRのケミカルシフトを例に解説しましょう。
メタンの4つの水素原子をハロゲン原子(F,Cl,Br,I)に変えて得られるハロメタンはメタンを含めて70種類存在します。ハロメタンの13C-NMR化学シフトはハロゲン原子数に対して非線型な関係を示すことが知られています。
元データは、共立出版の「ケモメトリックス」化学パターン認識と多変量解析、宮下芳勝、佐々木慎一から持ってきました。
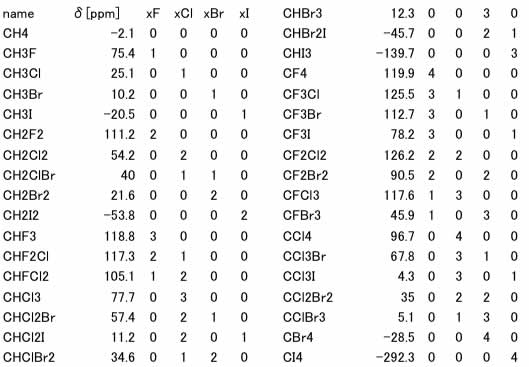
まず、ハロメタンの化学シフトとハロゲン原子数のテーブルを作成します。
そしてこのデータを元に予測式を作成します。
予測性能検証用のデータセットとしては次のものを使います。

重回帰法 (MR:Multiple Regression)
重回帰法はExcelにも搭載されており簡単に使えます。係数の意味合いも明確なので、様々な分野で使われています。
自作の解析用ソフトYSBhttps://www.pirika.com/Education/JP/MOOC/VSMR.htmlを用いて重回帰計算を行った所、
Chemica Shift = 29.6156*#F+14.5516*#Cl+-10.8588*#Br+-67.8264*#I+35.5578
となりました。
予測式を作るのに使ったデータセットでは、
Max Error=56.6ppm
Ave. Error=14.2ppm
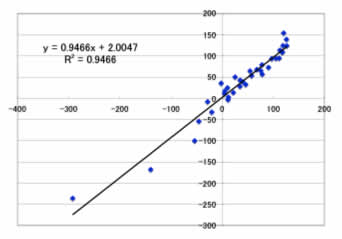
予測用のデータセットでは、
Max Error=30.3ppm
Ave. Error=17.7ppm

となりました。
PLS法(PLS: Partial Least Squares)
種本の「ケモメトリックス」では、QPLS法(Quadratic Partial Least Squares)による解析を行っています。
線形重回帰は、説明変数の間に相関を持つ場合(共線性)には適用できないので、PLS法を用います。PLS法の説明はこちら
PLS法に2次関数を導入したのがQPLS法です。
Chemical Shift = 33.5+40.7*#F+15.8*#Cl-11*#Br-49.9*#I-4*#F*#F-0.6*#Cl*#Cl-0.3*#Br*#Br-6*#I*#I-3.1*#F*#Cl+2.2*#F*#Br+9.8*#F*#I+0.8*#Cl*#Br-3.8*#Cl*#I-2.7*#Br*#I
最初の4つの項は重回帰と同じですが、その後ろに10個の相互作用項がつきます。
その相互作用の中に、#F*#Fなどが入るので非線形の回帰式になります。
Max Error=36.5ppm
Ave. Error=11.1ppm
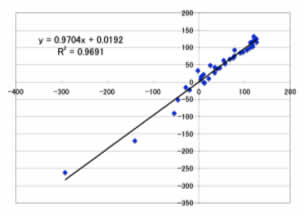
予測用のデータセットでは、
Max Error=22.4ppm
Ave. Error=11.7ppm
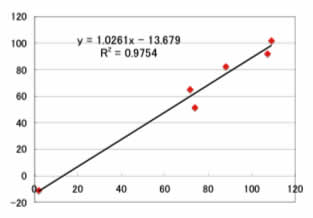
このように、線形の重回帰と比べれば改良されている事が判ります。
ニューラルネットワーク(NN)法(自作プログラム)
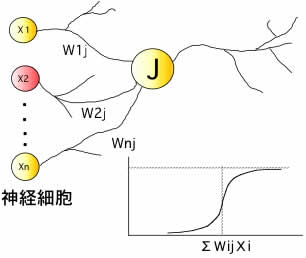
人間の脳を模した機械学習法のニューラルネットワーク法を用いると,
Max Error=6.5ppm
Ave. Error=2.2ppm
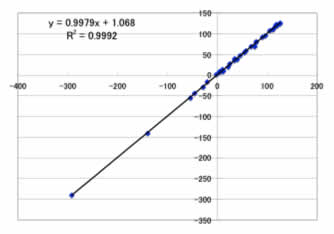
予測用のデータセットでは、
Max Error=3.3ppm
Ave. Error=1.9ppm
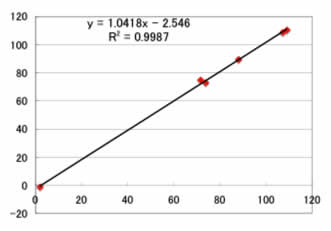
と非常に高い予測性能を発揮できますが、NN法は過学習などの問題点もあり使いこなしが非常に難しい解析法です。
また、式がブラックボックス化し情報の流れを追うのが難しいのも問題点です。
私は、ニューラルネットワークの学習過程に忘却効果を導入する、再構築学習法(../MAGICIAN/Examples/No6b.html)を使う事によってこの問題を回避しています。
多項式展開(PEM-現在はMIRAI法と呼んでいる)法(自作のソフトウエアー)
重回帰に非線形を導入する。
非線形性として、パワー関数(指数関数)、ガウス関数が選べます。
Chemical Shift=-302.46+43.844*
1.692*(EXP(-1*POWER((#F*0.323+-1.000),2)/POWER(1.375,2))+0.993)*
1.378*(EXP(-1*POWER((#Cl*0.164+-1.896),2)/POWER(0.995,2))+0.975)*
1.650*(EXP(-1*POWER((#Br*-0.184+0.064),2)/POWER(1.032,2))+0.846)*
1.505*(EXP(-1*POWER((#I*-0.326+-0.139),2)/POWER(1.875,2))+-0.540)
例えばガウス関数を選択すると上記のような予測式が得られます。
一つのガウス型関数は5つの変数を決めなくてはならないので、説明変数の数が増えてくると決定に非常に時間がかかるという欠点を持ちます。
Max Error=42.9ppm
Ave. Error=8.8ppm
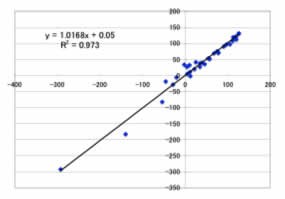
予測用のデータセットでは、
Max Error=14.1ppm
Ave. Error=5.0ppmとなりQPLSより予測性能は高くなります。
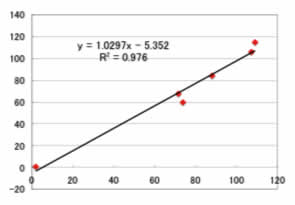
この方法の特徴は、フィードフォワード・タイプの変形ニューラルネットワーク法(../MAGICIAN/Examples/No6c.html)である事です。
方法論をまとめると、
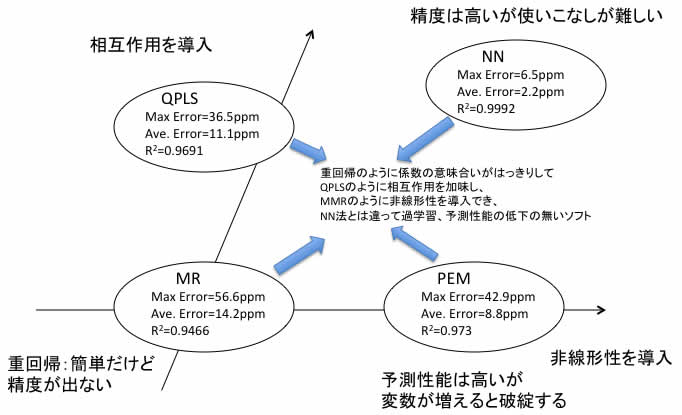
となります。
ここで、何故PEMでガウス型関数を用いたのかを説明しておきましょう。
3つの原子を固定して、残りをH, F, Cl, Br, Iと変化させ、ケミカルシフトをプロットするとFのところで山状になる事が下図からわかります。
ごのような上に凸の現象を記述するのにはガウス型関数が適していて、精度が高くなるのでしょう。
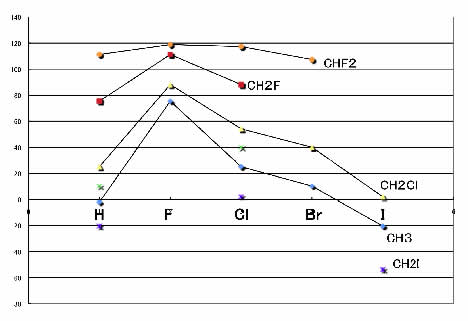
つまり、相互作用だ、非線形性だのと言う前に、物性推算式を作る前には、現象を良く考える事が重要なのです。
闇雲にやればできるなら、化学者がやる必要は無く、数学者、統計学者がやれば良いのです。
学生にはNN法やPEM法の解析ツールは提供していません。
解析ツールをいじくるよりも、先に「現象をよく考える」癖をつけてもらうためです。
YSBを用いた解析
授業で使っているYSB解析ソフトのクロスタームを導きだす機能はQPLSに近いです。
このYSBを用いてこの現象を解析してみましょう。
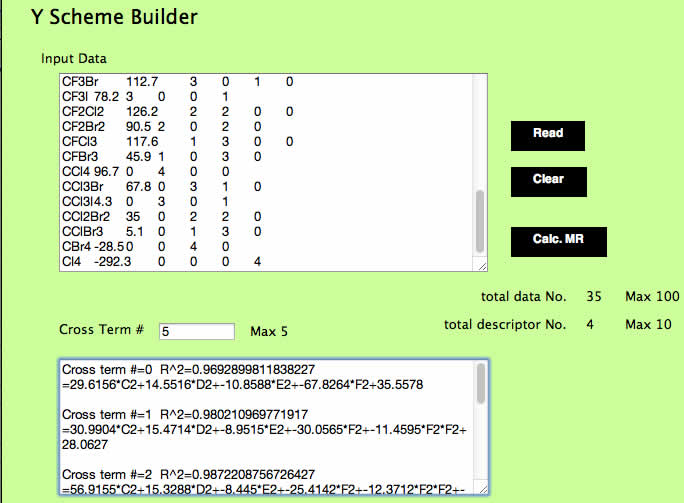
テーブルをコピーし、YSBのInput DataにペーストしてReadボタンを押します。
そしてCross Term #に5を入れてCalc. MRボタンを押します。
すると通常の重回帰(Cross Term=0)に加え、相関係数のR^2を高くするクロスタームを1から順に5つ選択した場合のモデル式を吐き出します。
ここでは、Cross Term#2の式をコピーし、表計算ソフトの2行目に貼付けてみてください。

選ばれたクロスタームはF2F2(ヨウ素ヨウ素)とC2*C2(フッ素*フッ素)の2つとなります。
式を構築したデータセットでは
Max Error=27.3ppm
Ave. Error=9.3ppm
予測データセットでは
Max Error=18.8ppm
Ave. Error=5.9ppm
となり、QPLSより精度は良くなります。
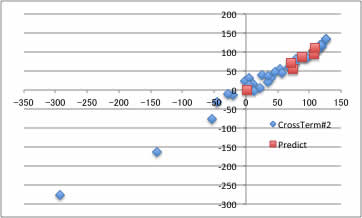
そこで、テーブルに、I*IとF*Fのカラムを継ぎ足し、再びYSBで計算を行います。

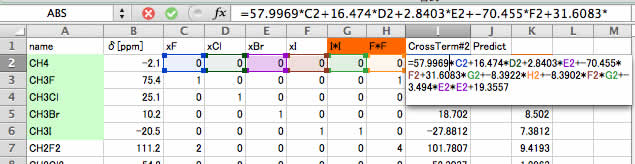
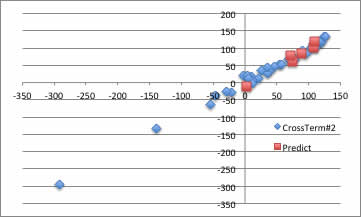
すると、次に選ばれたクロスタームは、F2*G2(ヨウ素*ヨウ素*ヨウ素)とE2*E2(臭素*臭素)となります。
式を構築したデータセットでは
Max Error=21.5ppm
Ave. Error=6.9ppm
予測データセットでは
Max Error=13.4ppm
Ave. Error=8.2ppm
このように、YSBをうまく使えば、予測式の構造は非常に明瞭なまま、非線形項を導入できる事がわかります。
課題:
Chemical Shift=a*F#+b*Cl#+c*Br#+d*I#+e*I#*I#+f*F#*F#+g*I#*I#*I#+h*Br#*Br#
aからhの係数を求めてください。
このように、物性推算式を構築しようとするのなら、現象を良く見つめる事が第1。
そして、式の意味合いを良く考え、ブラックボックス化しない事が第2。
そして本質を捕まえた上で、論文や特許に記載するモデル式は戦略的にどれを選ぶかを決めて行けばいいと思います。
相関係数だけを見て良い式だと判断するのは大間違いです。
情報化学+教育 > 情報化学 > ハロメタンのNMR・ケミカルシフト
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
