2003年頃の記事
情報化学+教育 > 情報化学 > 知識の獲得 > 過学習と予測性の欠如
ニューラルネットワーク法を用いて機械学習する際に良くであう問題、 過学習と予測性の欠如
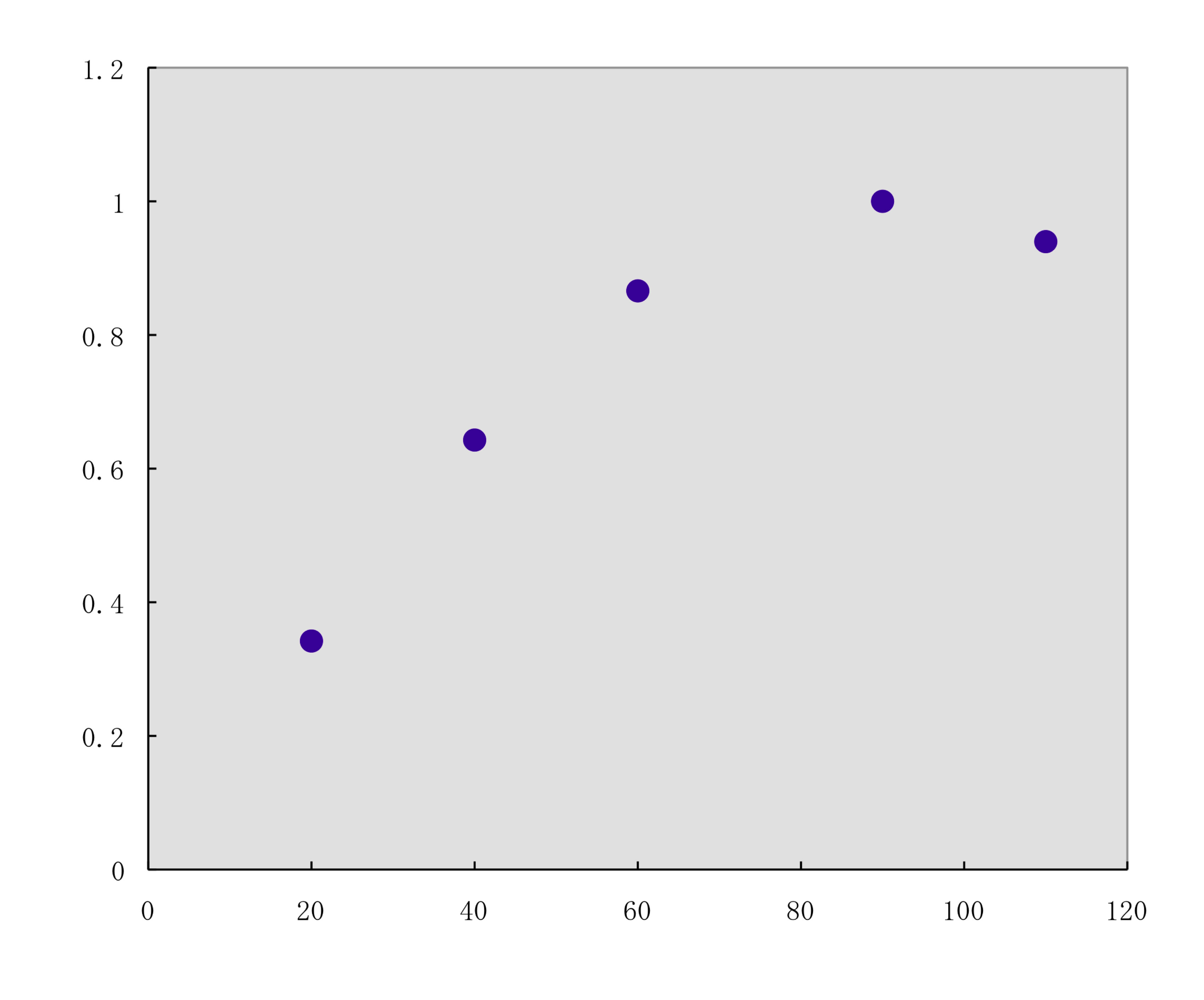
例えば、下の図のようなX−Y関係のデータポイントがあったとします。
化学系の研究者が最も一般的に用いる解析方法は、(重)回帰計算でしょう。
これは最小二乗法とも呼ばれる技術です。
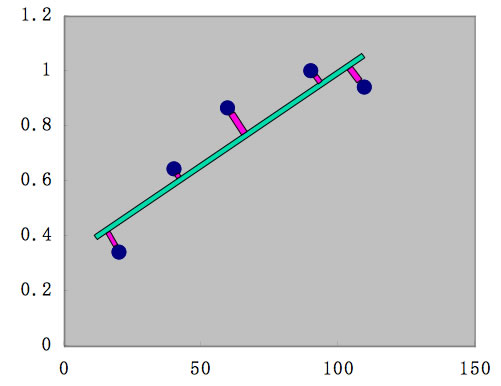
重回帰計算を簡単に説明すれば、下の図に示すように、緑色の直線、Y=aX+bを仮定して、この直線からの誤差の2乗が最低になるaとbの組を見つける計算です。
計算自体は非常に簡単で、Excelなどの表計算ソフトにもその機能が搭載されています。
多くの場合、化学の現象を扱うのはこの重回帰計算で十分です。
しかし、計算によっては非線形性を導入しなくてはならない場合があります。
実は、上の図の青い点は下に示すようにSinカーブの一部でした。
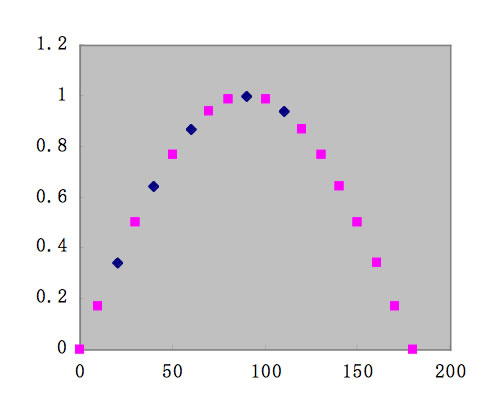
これを正しく扱いたい場合には、非線形回帰計算を行う必要があります。
そこで、先ほどの重回帰計算と同様に、
f(y)= A1* / [1+exp(-(B1*X1+B2*1))+
A2* / [1+exp(-(B3*X1+B4*1))+
A3* / [1+exp(-(B5*X1+B6*1))
という曲線を仮定して、誤差が最小になるA1-A3, B1-B6の組を見つけます。
曲線としてどんな曲線を仮定するは各人の自由ですが、ニューラルネットワーク法の多くはこのシグモイド関数を用います。
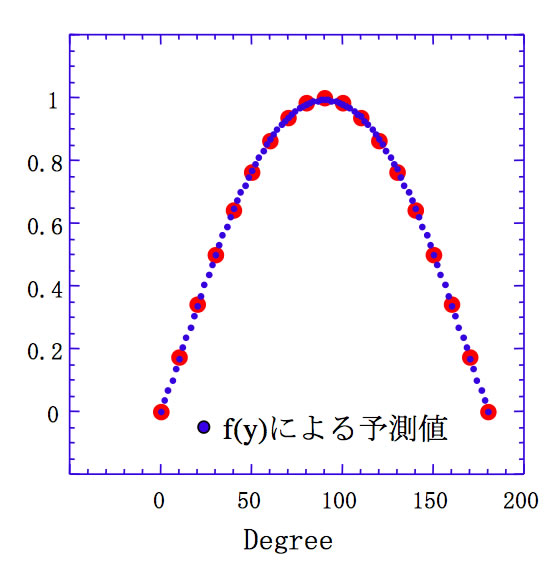
例えば、
A1= -2.14 B1=-1.84 B2=0.30
A2= -1.01 B3=0.04 B4=0.31
A3=2.11 B5=-1.87 B6=1.57
だとすると、上図に示すように良好にSinカーブを再現します。
これを、数学的に表すと、
- Algorithm
- 1. Since sin(-x) = -sin(x), we need only to consider positive x.
- 2. if x < 2^-27 (hx<0x3e400000 0), return x with inexact if x!=0.
- 3. sin(x) is approximated by a polynomial of degree 13 on
- [0,pi/4]
- sin(x) ~ x + S1x^3 + … + S6x^13
- where
- |sin(x)
- – (1+S1x^2 +S2x^4 +S3x^6 +S4x^8 +S5x^10 +S6x^12 )| <= 2^-58
- | x |
- 4. sin(x+y) = sin(x) + sin'(x’)*y
- ~ sin(x) + (1-xx/2)y
- For better accuracy, let
- r = x^3 *(S2+x^2 *(S3+x^2 *(S4+x^2 *(S5+x^2 *S6))))
- then
- sin(x) = x^3 + (S1*x^2 + (x *(r-y/2)+y))
*/
と級数展開になり、化学系の自分にはお手上げになります。
この、
f(y)= A1* / [1+exp(-(B1*X1+B2*1))+
A2* / [1+exp(-(B3*X1+B4*1))+
A3* / [1+exp(-(B5*X1+B6*1))
を模式的に書くと、生体の神経細胞(ニューロン)がつながったような図になる。
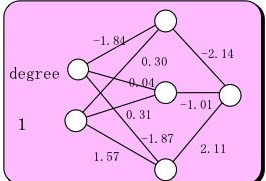
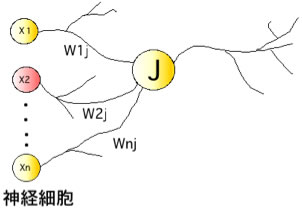
式中の変数、A1-A3, B1-B6は模式図中でニューロンを同士の結合の強さとして表す事ができます。
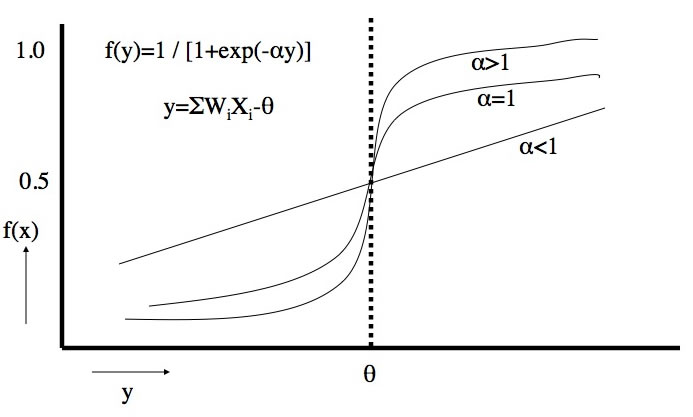
また、f(y)=A1* / [1+exp(-(B1*X1+B2*1))という関数は、シグモイド関数と呼ばれ、αの値によって、ある閾値θで急に値が変わる関数になります。
これは、生物の刺激ー応答曲線に似ているため、ニューラルネットワーク法と呼ばれています。
(全くもって取ってつけたようなネーミングで、当時は書籍が生物のコーナーに置いてあ離ました。)
前振りが長くなったが、過学習です。
コンピュータは人間と違い、飽きることを知らないので、命令すれば一晩中でも、1年でも学習を続けます。
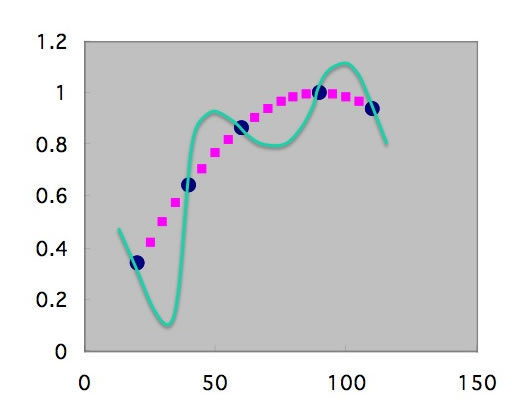
すると、本来欲しい点はピンクの点であるのに、最終的には学習した点をなめらかにつなぐ緑の線を答えとして提案します。
学習に使ったデータでは相関係数R=1.000、”おおー、ものすごく良くモデルを再現できる式が構築できた”と喜んで論文に投稿する事になります。
でも、上のグラフを見れば明らかなように、学習した近傍以外は非常に悪い答えを返すモデルです。
これなら、重回帰のほうがまだまし、っていうレベルです。
このように単純な系では、間違いはすぐにわかりますが、複雑な系では、過学習が起きたかどうかは非常に分かりにくいのです。
このような、過学習は、学習のデータポイントが少ない、NNの中間ニューロン数が多すぎるときに起こりやすいです。
そこで、ピンクの点も含めて学習させてしまうことを考えます。
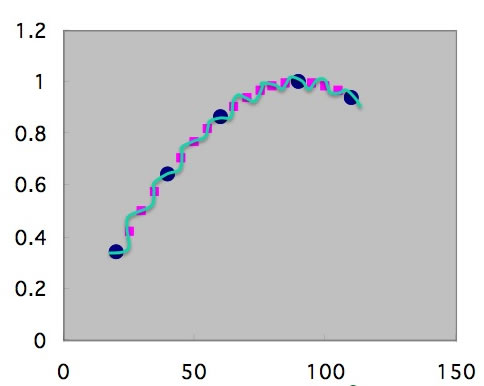
このようにデータ数が増えてくれば大きくハズレる曲線は取りようがなくなります。
これが、機械学習にはビッグ・データが必要という事につながります。
中間層のニューロン数は
f(y)= A1* / [1+exp(-(B1*X1+B2*1))+
A2* / [1+exp(-(B3*X1+B4*1))+
A3* / [1+exp(-(B5*X1+B6*1))
という式で、何個シグモイド関数を足し算して、この現象を表現しよううとしているかを表しています。
当然ニューロン数を増やせば複雑な現象にも追随できますが、その分、過学習という、やっかいも背負いこむ事になります。
こうした、中間層のニューロン数の最適化とデータポイントの数、これが考慮されずにニューラルネットワークを組んでも、無駄になります。
それを評価するのに赤池情報量基準(AIC)というものも知られていますが、難しすぎて自分には理解出来できていません。
それに、化学の現象はそれ以前に多くの、誤差、あやふやさを含んでいます。
古い資料であるがこちらを参考にしてください。あややなデータをもとにニューラルネットワーク法で推算式を組むとどうなるかを示してあります。
次に予測性の欠如の問題です。
先程のSinカーブの学習で、Sinの頂点までしか学習しなかったとします。
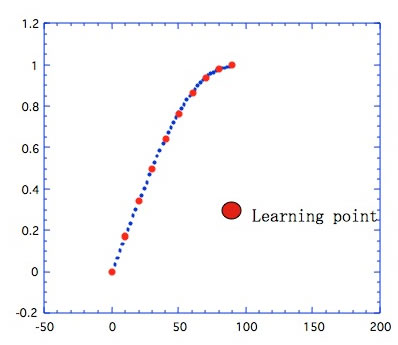
そうした場合は、学習した内側については、中間ニューロンの数が適当であれば、青い点が示すように良好に予測することができます。
これは、”内挿問題に対する予測性”は高いという言い方をします。
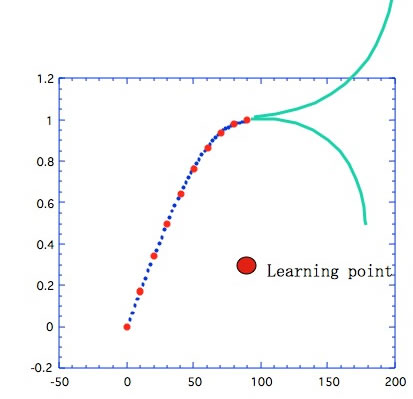
しかし、θが90を超えた先がどこに行くのかはNNには判りません。(実に人間にも解りませんが)
したがって1点でもよいから90度以上のデータを入れる必要があります。
これは実は先程の過学習よりも、よっぽどたちが悪い事です。
例えば、化合物の官能基を定義して沸点を推算するNNを構築しようとします。
ある官能基、例えば水酸基を持つ化合物の沸点のデータが水酸基が1,2,3個もつ化合物の沸点データがあり、NNに取り込んだとしましょう。
その場合は分子中に水酸基を4つもつものは、”外挿” 問題になり、予測性は高くないだろうと見当がつきます。
ところが、カルボン酸を1-2個もつ化合物、アミノ基を1-2個持つ化合物をNNに組み込んでも、分子中に、カルボン酸とアミノ基を両方もつアミノ酸をNNに組み込んでいなければ、これはやはり外挿になってしまいます。
こうした”組み合わせ”外挿はどれだけあるのかは、一般的に言えないし、非常にむずかしい問題です。
また、アミノ酸のように、ひとつの炭素にカルボキシル基とアミノ基が付いている場合、遠く離れて付いている場合でも物性値は大きく異なります。
従って、NNで物性推算式を構築した場合には、どのような母集団からNNを構築したのかが非常に重要な問題になります。
これに関しては、別の章で扱おうと思います。
Pirikaで構築した化合物の熱物性推算のNNはこれらのことを考慮に入れたNNを作り、公開しているので、世界中からのアクセスがあり、長い間にわたって高く評価されているのでしょう。
情報化学+教育 > 情報化学 > 知識の獲得 > 過学習と予測性の欠如
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
