2021.11.18
情報化学+教育 > MAGICIAN 養成講座 > 配合処方設計トップ > インクの配合処方設計
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
解析したいデータの例 No.1
JPA 2017197765 住友化学株式会社
インク組成物およびそれを用いて製造した光電変換素子
【課題】高い短絡電流密度が得ることができる2種の溶媒を含むインク組成物を提供する
【解決手段】 P型半導体材料と、N型半導体材料と、第一溶媒及び第二溶媒を含む2種以上の溶媒とを含むインク組成物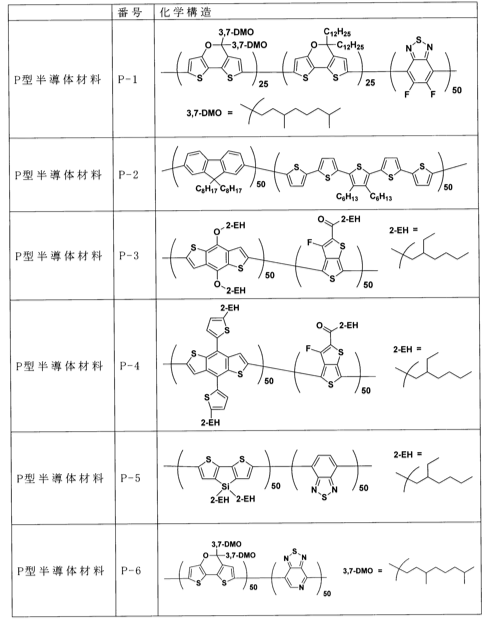
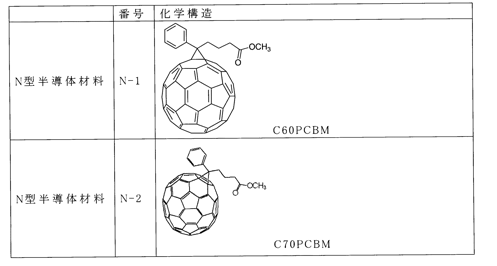
簡単に言えば、2種類のP, N半導体材料と溶媒を使って高い短絡電流密度を得たい、ということだ。
MIRAIには、誤差の取り方として、絶対誤差最小法(MAE)と最小二乗法(RMSE)の2種類が実装されている。
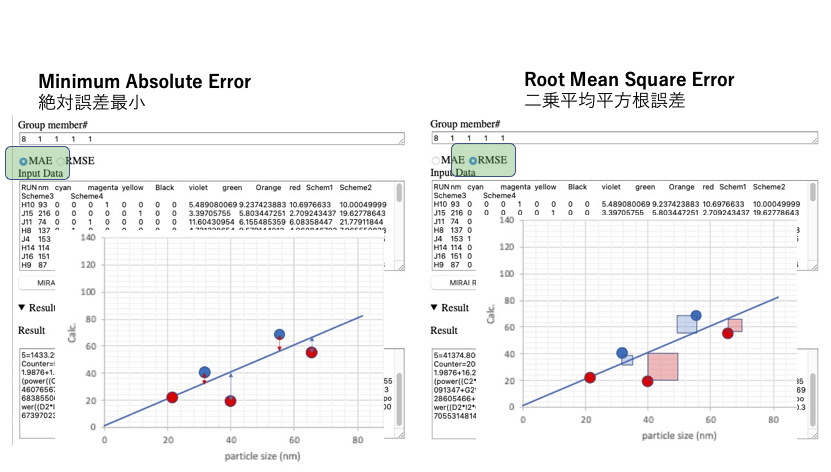
絶対誤差最小(MAE)を使うと、教師値と計算値の差の絶対値の総和を一番小さくしようと係数を定める。
すると、大きく外れるものはさらに外れ、他のものはどんどん直線に乗って来る。
入力間違いなど、怪しいデータを特定するときはとても有用である。
二乗平均平方根誤差(RMSE)を使うと大きな誤差を持つものを直線に近づけようとする。
小さな誤差を各点に割り振る。小さな誤差は2乗すると、とても小さくなり影響を与えなくなる。
通常の重回帰法は線形の最小二乗法になる。我々が開発しているGROVE法は線形で、絶対誤差最小法(MAE)と最小二乗法(RMSE)の2種類が実装されている。
この4種類の計算方法を比較してみよう。
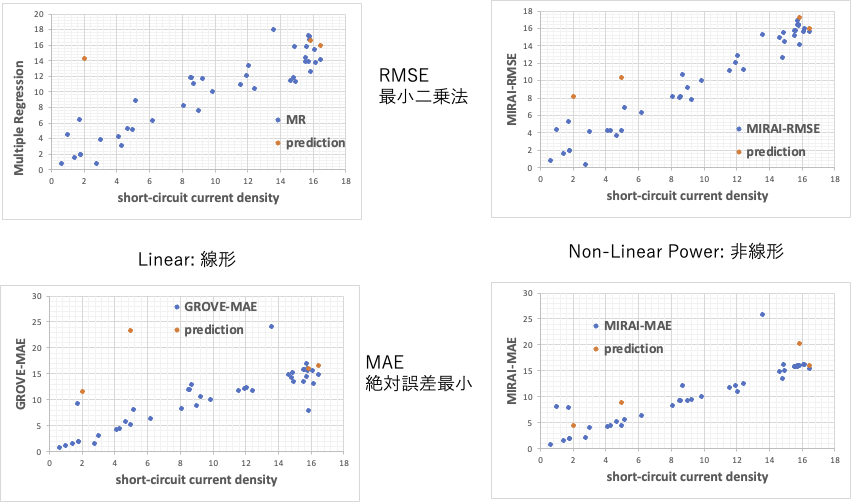
結果は非常に興味深い。絶対誤差最小法(MAE)の良いところが顕著に現れている。MIRAI法では4点ほど直線から外れる実験値があるが、他の実験データはとても良く直線に乗っている。GROVE法の線形回帰では外れるものが少し多くなる。
MIRAI-MAE=-0.711109708223613-1.9876+0.914100684455723*(POWER((C2*0.00139897779593369+D2*1.57286316326747+E2*0.459316763374167+F2*0.79208455297553+G2*0.416176033699134+H2*0.447101019803588+I2*1.18033013431262+1),-1.62322625599862)*POWER((J2*0.0141784947633641+K2*0.993413127403586+1),-0.197140814993588)*POWER((L2*0.712496600184694+M2*0.881951650719454+N2*0.857219822755202+O2*0.821396312322113+P2*0.874954323895292+Q2*0.876600285579374+R2*0.867819971929876+1),0.575503903570339)*POWER((S2*0.0660964156326232+T2*0.0589194116085574+U2*0.0761915385170714+V2*-0.067319122439351+W2*0.741296029168544+X2*0.584062650266498+Y2*1.4576390997673+Z2*0.756084846147299+AA2*0.68948901417174+AB2*1.13603652182674+AC2*0.72105108834501+AD2*0.679551754957941+1),0.39254413281453))
GROVE-MAE=19.5223853419192*C2+-1.1119987829629*D2+13.635889662213*E2+-33.1946528438729*F2+3.51214997788269*G2+3.01568949280795*H2+0.210431876492443*I2+-0.628346493842915*J2+-3.2134680487993*K2+0.0286425420396013*L2+-0.0559166550934589*M2+0.0251388725421847*N2+0.0321425563660525*O2+0.0115214405412037*P2+0.0163200308203588*Q2+0.221313871117952*R2+0.100613329541453*S2+-0.154906793667875*T2+0.0805114577484695*U2+-0.748286233122035*V2+0.870984166183338*W2+0.998102078873355*X2+1.80246152793306*Y2+1.55592764186324*Z2+1.7618094722351*AA2+2.16674683164456*AB2+1.68029239693249*AC2+0.997186452783814*AD2+0.104280213979893計算式をエクセルにペーストしてグラフを描き確認してみよう。
最小二乗法を使うと、全ての実験データをなるべく線から離れないように配置するように係数を求める。
通常の重回帰法とMIRAIのRMSE法は同じようなグラフを与える。
しかし、実際には、通常の重回帰法はこの系には使えない。
Multiple Regression=-9836.46508789062*C2+-9858.54162597656*D2+13104.0600585937*E2+-9884.50512695312*F2+-4925.63067626953*G2+-50816.1842041015*H2+-50818.9707946777*I2+45890.2221679687*J2+45884.8028564453*K2+-229.908722877502*L2+-0.48481382895261*M2+-0.465665870346128*N2+-229.905220985412*O2+-0.467298852279782*P2+-0.470624756067991*Q2+-0.292389723472297*R2+-229.836722373962*S2+-1.01680781599134*T2+-0.398298868909478*U2+-1.61014114879071*V2+0.234977908432483*W2+-0.592713546007871*X2+1.16497739963233*Y2+0.910294277593493*Z2+0.899858851917088*AA2+2.21961855888366*AB2+1.33116338774561*AC2+0.298248179256916*AD2+-40913.7219238281塗料の配合処方でも説明した。重回帰係数が、-9836とか13104とか大きくなると、処方が」少し変わっただけで結果がとんでもなく大きく変動してしまう。
例えば、適当なP-1の量を0.5から」0.4に変えてみよう。結果は100倍ぐらい変わるだろう。MIRAI法やGROVE法ではほとんど影響ない。
そこで、実験データが少ない、非線形性がある、識別子が多い配合問題に対して、解析ツールを重回帰法しか持たない場合には、解析がお手上げになる。
MIRAI-RMSE=-6.24098259691519-1.9876+0.0290997780996556*(POWER((C2*0.79961601373615+D2*-0.333783413199201+E2*0.485909140176266+F2*0.635411236356317+G2*0.146744396313107+H2*0.113057540797912+I2*-0.141671856971961+1),1.26047602045767)*POWER((J2*0.0647186619502536+K2*-0.2336706808163+1),0.573046338397967)*POWER((L2*0.446243593708213+M2*0.394040306635662+N2*0.412339305024572+O2*0.45711578001346+P2*0.406529561446594+Q2*0.407905851800118+R2*0.363945286858518+1),1.56674101529224)*POWER((S2*0.311648720079908+T2*1.08165537325029+U2*10.0045442065987+V2*0.270924450988719+W2*14.2685499106683+X2*8.34051502003881+Y2*21.7253204533158+Z2*12.2756278866944+AA2*13.0995716768295+AB2*53.6416820031627+AC2*16.4042590463573+AD2*10.6801109239021+1),0.122155998621232))MIRAI法は指数関数の掛け算で物性を予測する式を作成する。今回は、P型半導体、N型半導体、第一溶媒、第二溶媒の4グループに分割した。
その影響をグループごとに見てみよう。
G-P=POWER((C2*0.00140344242566633+D2*1.5733663100677+E2*0.459314152899126+F2*0.791907632723531+G2*0.414921506791787+H2*0.447101019803588+I2*1.18077252036854+1),-1.62324615257733)
G-N=POWER((J2*0.0141643272016091+K2*0.99346603458404+1),-0.19698481440908)
G-S1=POWER((L2*0.712633416087653+M2*0.881951650719454+N2*0.857219822755202+O2*0.821528407786171+P2*0.874954323895292+Q2*0.8765977441452+R2*0.868343433314093+1),0.575503903570339)
G-S2=POWER((S2*0.0665252673754605+T2*0.0589073575565699+U2*0.0757826281133001+V2*-0.0673197887365997+W2*0.740515459060242+X2*0.584206427350649+Y2*1.45760970755326+Z2*0.754530058934956+AA2*0.689499274125841+AB2*1.13569141761498+AC2*0.722610422103112+AD2*0.679265342375855+1),0.392539583705509)グループのメンバーの少ないG-Nで説明しよう。
G-N=POWER((J2*0.01416+K2*0.993466+1),-0.19698)
(J2*0.01416+K2*0.993466+1)の部分を指数関数の底と呼ぶ。
カラムJは、N-1半導体の使用量が入る。カラムKにはN-1半導体の使用量が入る。
半導体の量が同じ量であっても、係数が70倍も違う。そこで括弧の中身は変わるが、指数が-0.19698なのが大事だ。
指数がマイナスの時には、減少関数になるが、値が小さい時には緩やかな減少となる。そこでPower関数としては最小値0.872、最大値0.997と大きくは変動しない。
パワー関数に分けて考える。
それぞれのグループの、パワー関数の変換後のグラフは次のようになる。
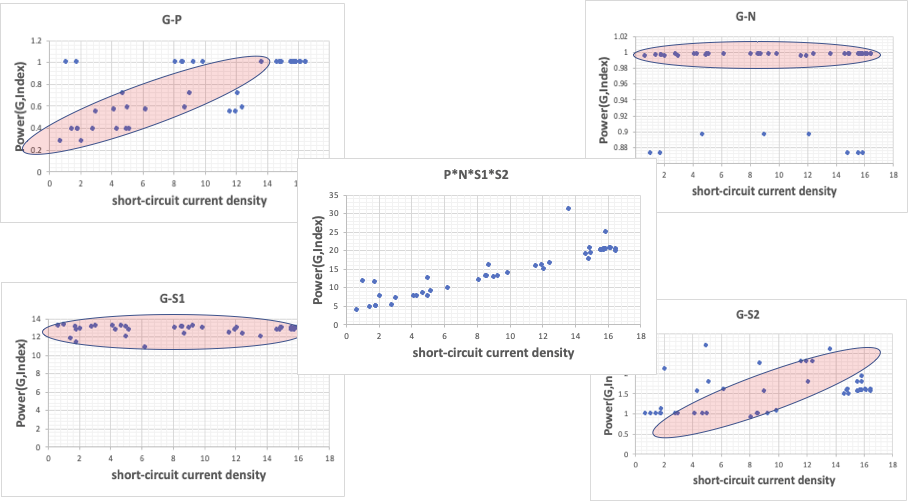
そして、4つのパワー関数をかけたものは中央のグラフのように、短絡電流密度と非常に高い相関となる。
この時、パワー関数の掛け算なのがMIRAIの特徴になる。
足し算では、全体を4分割する取り方は無限に存在する。そして、さらにその中身を分割する。解を一つに決められないし、グループごとの相互作用は表現できない。
このように解析することによって、実験I-13の予測値が大きく乖離するのは何故かを考えることができる。
グループ溶媒2の値が大きいことがこの結果につながっている。
それでは、こうした推算式ができたら次に行う応用をやってみよう。
コンピュータによる組成設計
例えば、実験 I-10を改良して、さらに高い短絡電流密度を得ることを考えてみよう。
P型半導体とN型半導体の種類と量は固定にして、溶媒1と溶媒2の量を変えることを考える。
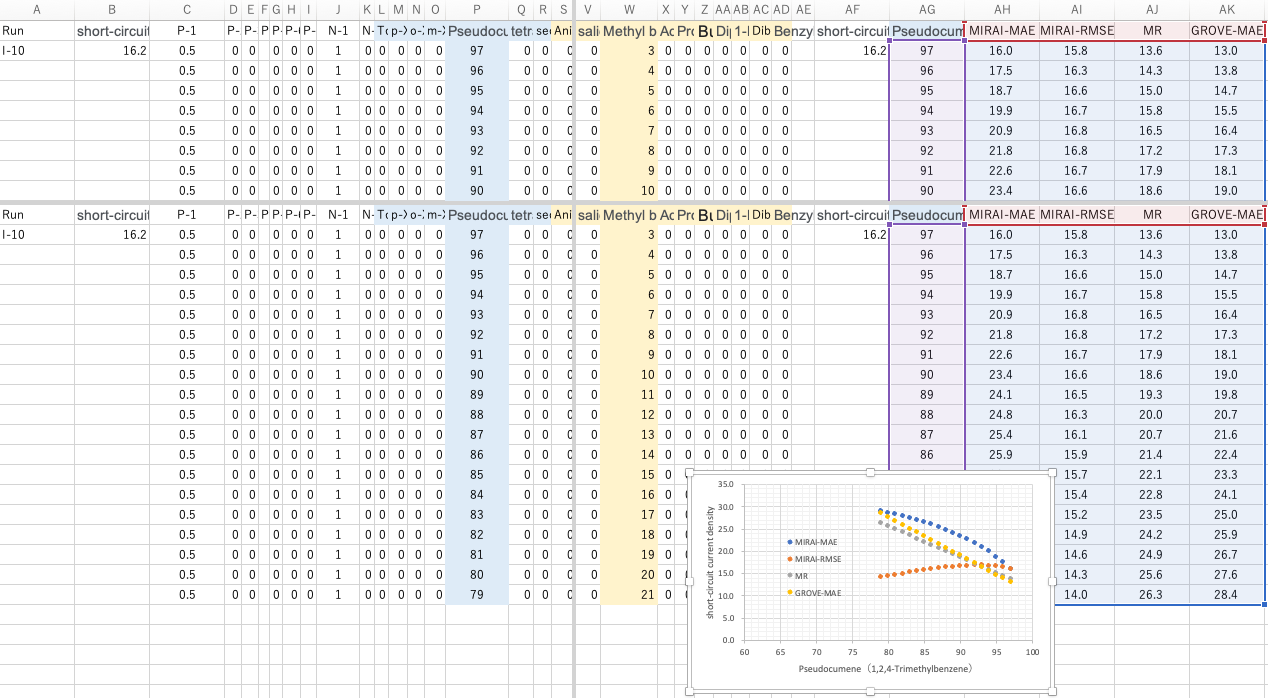
他の部分は共通にして、Pseudocumeneの量を97から1ずつ減らし、Methyl benzoateを3から1ずつ増やし全体の量は変えない。
我々は推算式をすでに持っているので、各溶媒組成の時の短絡電流密度を推算することができる。それをPseudocumeneの量に対してプロットしてみる。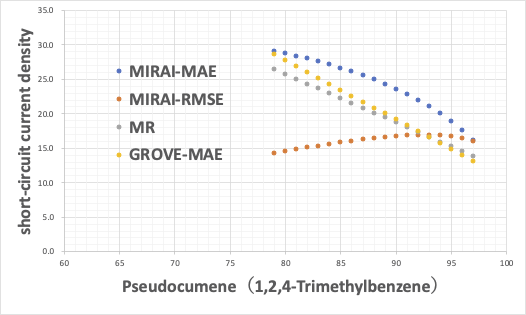
これは、先程のI-13が乖離する理由をちゃんと考えた場合と、そうでない場合とで解釈が逆転するだろう。
解釈がきちんとできていなくても、明日やる実験をこののように決めて、試してみたらこうなった。その結果をMIRAI式にフィードバックして次の実験を決めていく。そうする事で最適値にたどり着くのは非常に速くなる。
私の解釈では、MIRAI-RMSEの上に凸になるのが正しく、他の3つは間違っていると考えている。ランダム・フォレストで多数決とは異なる意見になる。とは言っても試しようがないが。
解析したいデータの例 No.2
Patent WO2011/034019 日立化成
印刷法用インクおよびそれに用いられる金属ナノ粒子、並びに配線、回路基盤、半導体パッケージ
Cu及び/又はCuOを含む金属ナノ粒子を含む印刷法用インク。
分散剤などの添加剤を使用せずに良好な分散性と継時的な分散安定性。
1次粒子の体積平均粒径 D(nm)の金属ナノ粒子と分散媒を含み、
金属ナノ粒子同士の平均粒子間距離L(nm )が、1.6≦L/D≦3.5の関係を満足すれば、
分散剤無しで分散性に優れる印刷法 用インクが得られる
分散媒がハンセン溶解度パラメータにおける極性項が11MPa0 . 5 以上の 有機極性溶媒
これまでと同様に通常の重回帰法、MIRAI法で分散性を表すモデル式を作成する。
実験データは全てモデル式の作成に用いた。
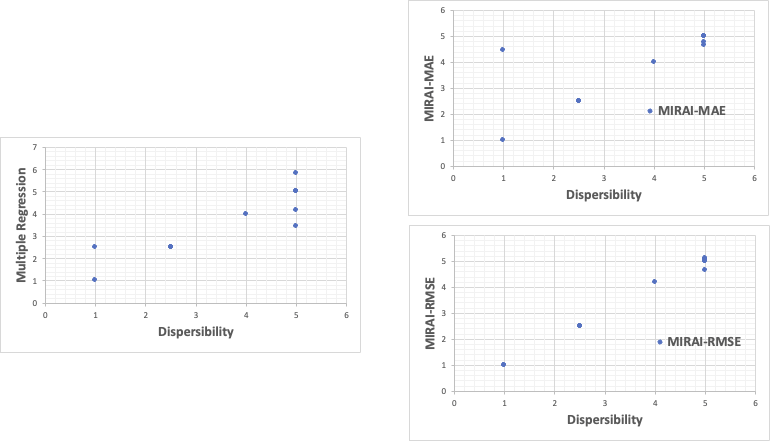
通常の重回帰法ではあまり精度が出なかった。これはMIRAIの計算結果から考えて非線形性がある為と考えることができる。
MIRAI-MAEで大きく外れる実験CE-13はE-13とL/Dの値が違うだけである。
L/Dの取り扱いが、MIRAI-MAEとMIRAI-RMSEで次のように異なる。
MAE: POWER((L2*2.25290833017326+1),0.175039513884569)
RMSE: POWER((L2*-0.357670241635847+1),7.13042013209691)係数の意味を考える
MIRAI-MAEとMIRAI-RMSEのどちらを選ぶかは、読者に任せよう。
この特許では、溶媒8種類を使って実験を行なっている。
POWER((Solv1*0.0821+Solv2*0.2620+Solv3*0.1432+Solv4*0.1037+Solv5*1.0542+Solv6*1.0546+Solv7*1.0539+Solv8*0.9665+1),1.29322)MIRAI-RMSEでは各溶媒の係数をこのように決定している。
この係数の大小が何に起因するか、検討してみよう。
溶媒のSMILESの構造式から、YMBを使って物性推算を行う。
すると2列目にMIRAIの係数、3列目以降は物性値の一覧表を作成することができる。
どれか、一つの物性値を選ぶなら、表面張力が高い物性ほど係数は大きくなる。
2つの物性値から、重回帰式を作ると、次のように、水への溶解度、ヘンリー定数から係数を予測することができる。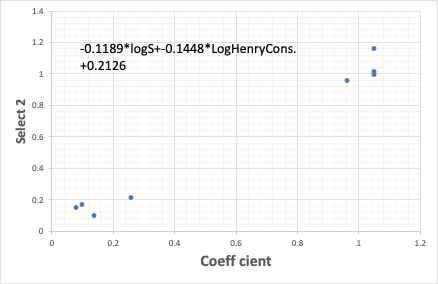
このように、係数が予測できるようになれば、任意の溶媒に変えた時の予測値を得ることが可能になる。
後はAIに任せて、全ての溶媒を片っ端からスクリーニングして、良いものを全部特許取って仕舞えば良いだけになる。
解析したいデータの例 No.3
Patent JP 6521138 B1 東洋インキ
樹脂(A)と、導電性微粒子(B)と、溶剤(C)のインク
もう、自分で解析できるだろう。
ただし、logY1の値をわざと間違って入力してある。
実は、本当に打ち込みの時に間違って入力してしまったものだ。
ニューラルネットワーク法などは、中身がブラックボックスになり、情報の伝達が見えなくなる。そして、間違った値を入れてもそれが正しいとして学習してしまう。
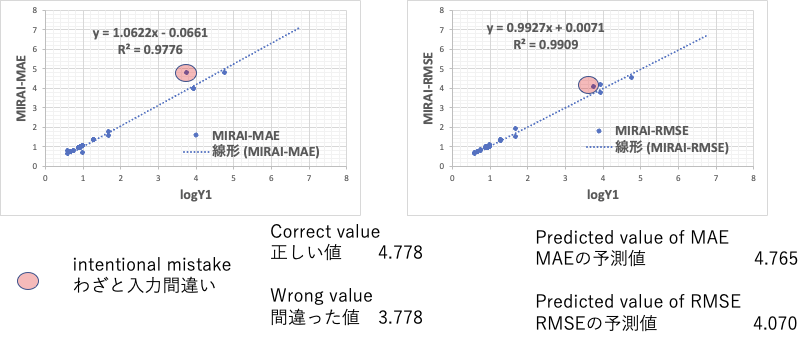
MIRAIのMAEで計算するとわざと間違えたものが直線から遊離してくる。
しかもその計算値は4.765と正しい値4.778にとても近い値を予測する。
間違った値を入力しても、正しい値を予測することができると、データを綺麗にするのにとても役に立つ。
MIRAIのRMSEで計算した結果が通常のMIなどで出てくる結果で、どれが汚いデータなのかはわからなくなる。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
