2021.10.30
情報化学+教育 > MAGICIAN 養成講座 > 配合処方設計トップ > 配合処方解析ツール、MIRAI
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
MIRAI(Multiple Index Regression for AI) データ数が少ない、識別子が多い、非線形性があるケースに使う解析ツール。
解析したいデータの例
JPA 2021165831 (ナガセケムテックスの特許)
【課題】充分なレジスト剥離性を維持しつつ、保存安定性に優れたフォトレジスト剥離液を提供する。
データは次のようにまとめられている。
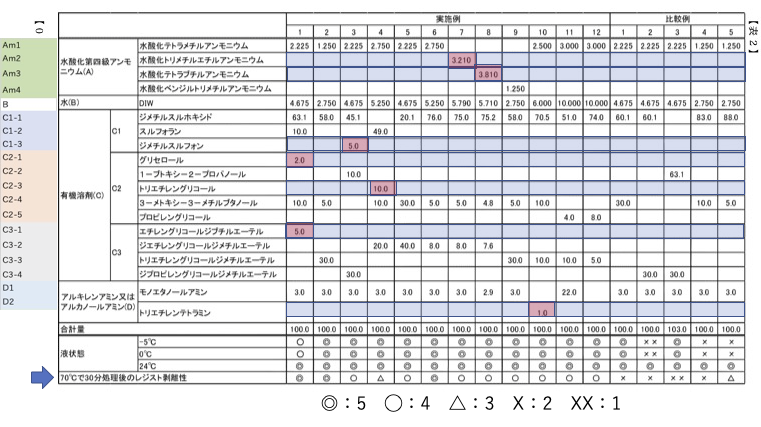
特に、70℃で30分処理後のレジスト剥離性を予測することを考えてみよう。
実験データの総数は高々17個しかない。
しかし、剥離液の成分は、19種類ある。
そしてこのテーブルの特徴は、ほとんどの部分が空欄である事だ。
青くマークした成分は、一回しか使われていない。
解析する立場からすると、これは不都合だ。一回しか使われていない成分は、計算誤差を吸収してしまうので記述性は非常に高くなるが、係数自体は無意味になる。
実験データのうち3つを予測データにしたので、14実験データを19種類の識別子を使って解析する事になる。
連立方程式を解くには変数の数より式の数が多い必要がある。例えば、Excelの回帰分析機能を使って強引に計算してみよう。係数は求まるかもしれないが、答えに意味がないことはすぐにわかるだろう。
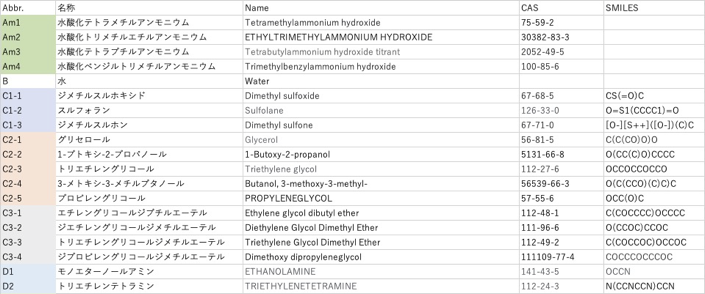
Materials Integration(MI)、材料複合化の研究者を目指すのなら、次のデータをExcelなどにペーストして、自分で計算してみよう。
MIRAI method
我々の開発した、 MIRAI(Multiple Index Regression for AI)を使うと結果は次のようになる。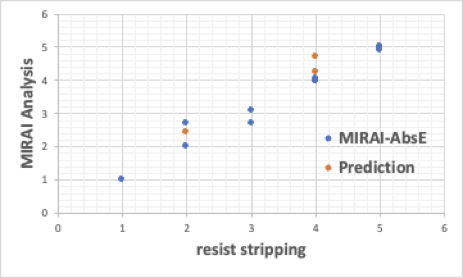
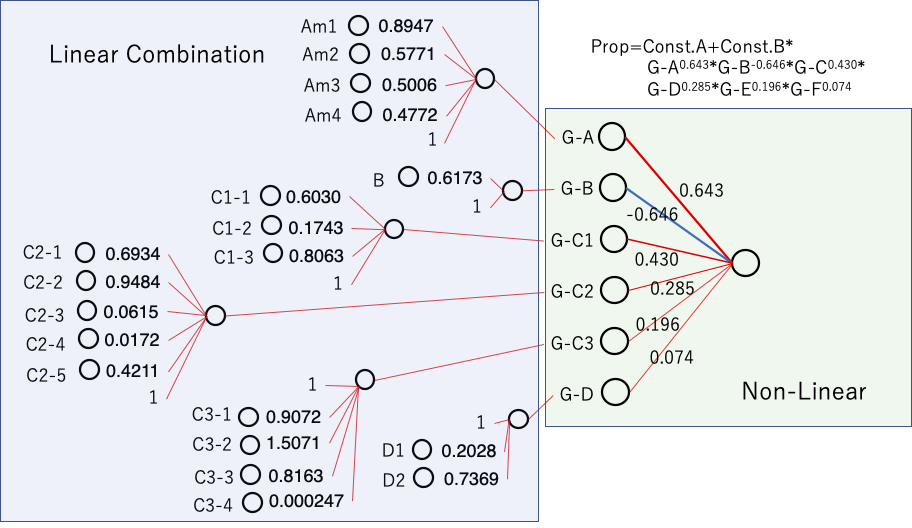
MIRAIで解析を行うと、次のような解析結果が得られる。
Resist Stripping =-1.172 + 0.7715* (G-AM0.6430 * G-B -0.6459 * G-C10.4303 * G-C20.2851 * G-C30.1963 * G-D0.0741 )
両辺を整理してlogをとると、複数の(Multiple)指数(Index)の部分がlogの前に出るので重回帰(Regression)式になる。
そして似た性質の識別子を1つのグループとして考える。この場合には6グループとなり、データ数14より随分と小さくなっている。そして各グループがパワー関数となる事によって、非線形性が表現される。最後にグループ間が掛け算されることで、グループ間の相互作用が導入される。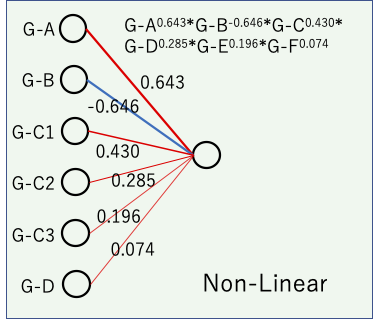
そして、グループの中では、各メンバーは線形関数で表現する。パワー関数の底は0以上である必要があるので1を足す。
水酸化第四級アンモニウムの場合、
G-AM: 0.8947*Am1+0.5771*Am2+0.5006*Am3+0.4772*Am4+1
この係数を比較すると、例えば、Am4の係数はAm1の半分しかないので、使用量を倍にししないと同じ性能が出ないことがわかる。
Water, 水:
G-B: 0.6173*B +1
C1
G-C1: 0.6030*C1-1 +0.1743*C1-2 +0.8063*C1-3+1
C2
G-C2: 0.6934*C2-1+0.9484*C2-2+0.0615*C2-3+0.0172*C2-4+0.4211*C2-5+1
C3
G-C3: 0.9072*C3-1+ 1.5071*C3-2+ 0.8163*C3-3+ 0.000247*C3-4+1
Alkanolamine
G-D: 0.2028*D1+0.7369*D2+1
各グループは掛け算されるため自由な値は取れず、項目間の相互作用が表現される。
結果として、非常に少ない実験データ数で、非線形性と項目間の相互作用が導入された予測性能が非常に高いMIRAI式を得ることができる。
これは、ある種のフィード・フォワード型のニューラルネットワーク法と見なすことができる。通常のニューラルネットワークと比べ、入力ニューロンと中間ニューロンの結びつきは疎になる。
重回帰法
同じデータを、重回帰法を用いて解析してみよう。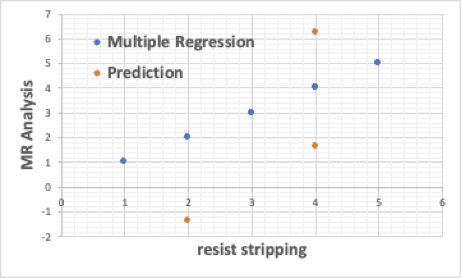
MR式を作るのに使ったデータは全て綺麗に直線に乗っている。
これは実験データ(予測用の3点を除く)の数より、識別子の方が多い場合に起こる。
そして予測のデータは3点とも大きく外れる。
つまり、通常の重回帰解析は全く無意味であると言える。
主成分解析:Principal Component Analysis(PCA)
データ数より説明変数が多いような系では、主成分解析(PCA)を行って、次元圧縮を行うと教えている教科書は多い。
例えば、下図のように2次元のデータポイントがあった場合に、XY軸を回転して、X’Y’とした場合にはY’はほぼゼロになるので、X’軸の読みだけで各ポイントを表すことができる。つまり、2次元データを1次元データに圧縮することができる。
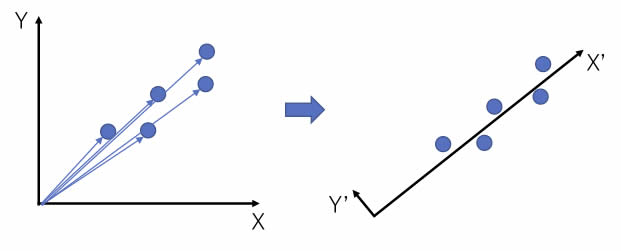
PCA解析はpirikaのページで計算できるので試してみて欲しい。
ただし、実際に計算してみると次のようになる。
主成分をいくつ組み合わせれば、この実験結果を表現できるか? 10個組み合わせても92.14%しか表現できないことがわかる。
つまり、このケースでは、ほとんど次元圧縮が効かないことをこの結果は示している。
それは、ある意味当たり前である。実験の1,3,4,7,8,10ではその実験でしか使っていない成分を使っている。その6個分の次元はどうやっても圧縮できない。
10個の主成分を使って、主成分回帰を行った。10変数を使い、実験データ14個で重回帰式を作り、3つを予測した。
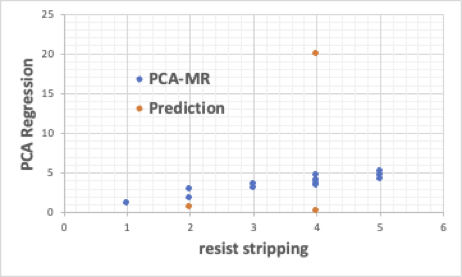
この場合も、予測値は大きく実験結果から乖離していた。
おそらく、PLSを使っても同様に次元圧縮はできないと思われる。誰か試した人がいたら教えていただきたい。
ビッグデータがない以上、ニューラルネットワーク法は問題外だろう。
このような配合処方の解析に関しては、どういう解析ソフトを作ったら、その解析が可能になるか?の視点が必要になる。
誰かが、Phythonで作成してライブラリーにあげてくれるのを待つのであろうか?
実験化学者はそれでも良いかもしれない。MIの専門家であるなら、クライアントのこうした要請にもすぐに答えなくてはならない。「ビッグデータ、ビッグデータ」と歌っていれば良いものではない。
さらに先に行こう
この特許では、Am2,Am3,Am4は実験No7,8,9でしか使われていない。Am1と比べ性能が低いので使われなかったのかもしれない。しかし、その分量を増やしたら、評価点として6点、7点が現れるかもしれない。
一度MIRAI式が構築できたら、後はAIに任せてさらに良くなる処方を探索させるのも簡単であろう。(逆に言えば、特許を出す前に、自分でチェックするべきであるが。)
AI先進国はこうして日本の特許を狙い撃ちにしている。まー昔、日本はアメリカに対してそれをやったのだから文句は言えないが。
ここでは、更に高度な特許破りの方法を考えよう。
特許破り
この特許では、C1, C2, C3の溶媒をハンセンの溶解度パラメータの分極項(dP)と水素結合項(dH)の範囲で規定している。それを図示すると下の図になる。
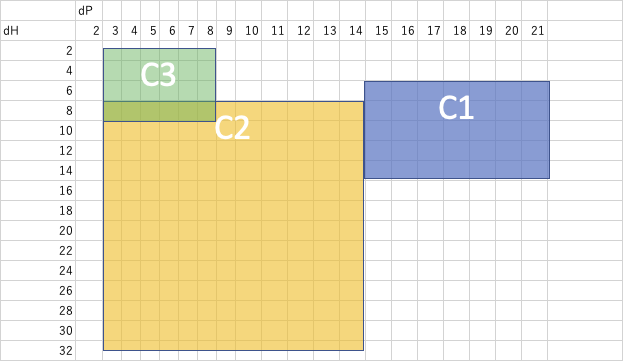
これは非常に広い範囲すぎるので、反例(範囲に入るのに性能の出ない例)はいくらでも見つかるだろう。
しかし、それをやって特許を潰しても余り面白くはない。
例えば、C2グループの溶媒を考えてみよう。5つの溶媒の係数は次のようになる。
G-C2: 0.6934*C2-1+0.9484*C2-2+0.0615*C2-3+0.0172*C2-4+0.4211*C2-5+1<br>
もしこの係数が予測でき、さらに大きな係数を持つ新たな溶媒が探索できるなら、研究は非常に加速する。
普通にHSP値を説明変数にして重回帰を計算すると、係数を予測することができるようになる。
MIRAIの係数=1.3860*dD-0.6928*dP+0.3197*dHacid-0.1120*dHbase-17.733657408806
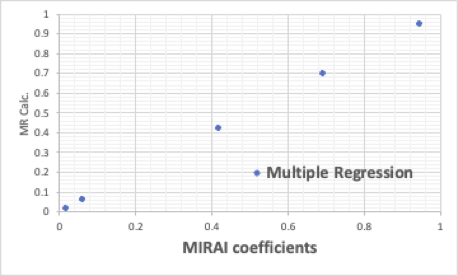
後はHSPiPを用いて、特許のレンジにはいる化合物を検索し、上記計算式で計算し、ソートして係数の大きいものを選び出せば良い。
当然、剥離液は溶解しすぎてもダメだし、安定性など、他の条件も加味する必要はある。
しかしながら、こうした式を構築できれば、その後の処理は非常にAIと親和性が高い。
これがMIRAIという名称の由来だ。
慣れれば、非常に高速にサイクルを回せるようになる。<br>
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
