2018.9.3
情報化学+教育 > MAGICIAN 養成講座 > 講義資料 > 第3a回ポリマー設計と重合シミュレータ -POSEIDON-
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
量子化ベルト
マテリアル・インフォマティクスを使って高分子を設計しようとした場合、ガラスや触媒などと異なりポリマー特有の設計の難しさに遭遇します。
中々うまく説明できなくて困っていた所、ある人から面白い例え話を聞きました。
「あなたのしているのは、量子化ベルト? それともアナログ・ベルト?」という言い方があるらしいです。
量子化ベルトというのは、ベルトに穴があいているタイプのもので、アナログ・ベルトというのは長さを自由に変えられるベルトの事をいうらしいです。
原子の周りを飛び回る電子は、自由な軌道を取れるわけでは無く、量子化された軌道のみを回ります。
それと同じでベルトの穴の位置にしか長さを調整できないので量子化ベルトと呼ぶのでしょう。
これと同じことがポリマーの設計でも起こります。
様々な高分子が設計され、その物性値がPolymer HandbookやPolyInfoデータベースに収録されています。
Van KrevelenやJozef Biceranoらのポリマー物性推算式なども開発されています。
こうした物性推算式は基本的にはポリマーのモノマー単位ユニット中に入っている原子団の数を元に計算されます。
マテリアル・ゲノムとポリマー物性推算式を使って材料開発しようとすると、「ある材料の他の物性はそのままに耐熱性を上げたい」という要求が出てくる事があります。
するとポリマーの単位ユニットのある部分にXXという官能基を入れろとかいう答えになってしまいます。
では、新しいモノマーを開発する?
でも、そうすると他の物性も変わってしまう。
つまりポリマーの骨格はモノマー単位に量子化されていて、ある物性だけを独立には変更できません。
通常できあがったポリマーには様々な材料(安定剤、顔料、フィラーなど)が添加されます。
これらの添加剤の量はアナログ量で加える事ができます。
こうした量子化量とアナログ量のバランスを取るのがポリマー開発の面白みであり、難しい所です。
一種のアートであり、AIには難しいところであるかもしれません。
しかし、そんな悠長な事を言っていると、
「3つのMI」、
Materials Informatics(物質情報学)、
Materials Integration(材料複合化)、
Materials Infrastructure(材料製造基盤)
を駆使して材料設計を行なっているMI先進国に2周-3周遅れになるので取り敢えずスタートしましょう。
第3a回ではMaterials InformaticsとMaterials Infrastructureについて解説します。
Materials Integrationに関しては第3b回で解説する事にします。
ポリマー材料の基本骨格設計
高分子の基本骨格設計には主に2種類ある。
全く新しい単量体(モノマー)を設計してしまうやり方と、モノマーの配合処方を設計するやり方があります。
新しいモノマーを設計する方法は接着剤や光学用高分子など特殊なポリマーでは多いですが、ポリマーの製造設備の問題、化審法対応などコストが上昇する要因になるので、高機能で利益率の高いポリマーにしか適用できません。
こうしたモノマーの設計にはポリマー物性推算式は大いに役に立つと思われます。
それに比べ、モノマーの配合処方を設計するやり方は、多くの企業で普通に行われている方法です。
すでにある処方で作られているポリマー材料のある物性を、目的に合わせてチューニングするのに、モノマー比を変更する、他のモノマーに変更するなどを繰り返します。
後者の設計には重合シミュレータなどの利用が欠かせません。
筆者が自作したラジカル重合シミュレータ、POSEIDONを使った設計方法を紹介します。
ポリマー材料の複合化設計
ポリマーには、安定剤、顔料、フィラー、可塑剤、溶剤など様々な材料が複合化されて一つの製品に仕上がっています。
そうした複合化設計に対してはMaterials Integrationのやり方が有効であることが多いです。
ポリマー・アロイやポリマーブレンドの設計に関しても広義には複合化設計に分類されるのでしょう。
企業での研究であれば、膨大な実験データがあると思われるので、すぐにMaterials Integrationに取り掛かれるでしょう。
ポリマー材料の製造基盤
ポリマーは一口にポリマーといっても、ラジカル重合ポリマー、縮合系ポリマー、付加重合系ポリマーなど多くの種類が存在し、重合方法もバルク重合、懸濁重合、溶液重合、乳化重合など、使用する系、目的に合わせ選択されます。
新しい触媒などが開発されると製造プロセスも変更になるので最適化が必要になります。
友人のJoback先生とは、マテリアル・ジーノムに対抗して、プロセス・ジーノムでモノづくりしようと研究を進めています。
重合シミュレータの結果から示唆される製造プロセスもあるので3つのMIは独立している訳ではありません。
ラジカル重合性高分子の化学
ポリマーは小さなユニット(2重結合を持つモノマー)が連結してできています。

この部分は[高校生にもわかるシリーズのMAGICIAN-Jrリンク切れ]()で焼き鳥を使って詳しく説明しています。
ギネスに挑戦。世界一長い焼き鳥
モノマーは1種類だとは限りません。
同じ比率のモノマーが導入されていても物性は異なります。
ランダムポリマー
完全交互共重合ポリマー
ブロックポリマー
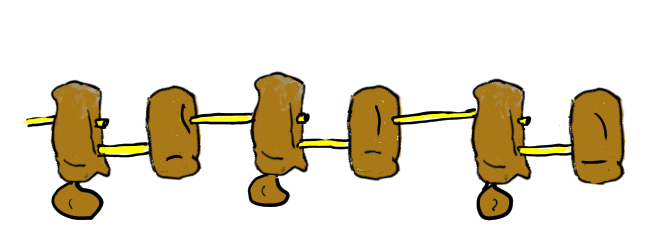
連結の長さは分布を持っています。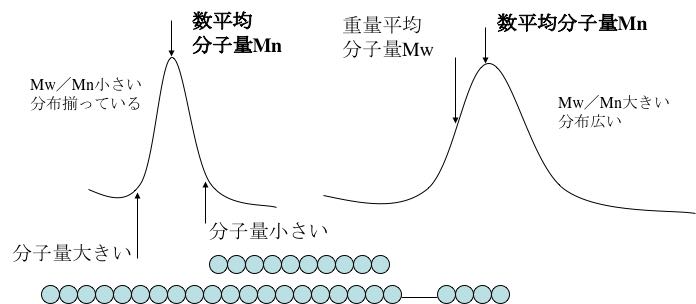
重合の初期と、後期で組成が変化します。枝分かれするポリマーもあります。
以上のように、人間の作るポリマーは天然のポリマーと比べ均質性が非常に劣るという特徴を持っています。
このような人工的な高分子を設計しようとした場合、データベース中に存在するポリマーの物性値がある値になったとしても、ポリマーのゲノム=遺伝子(モノマーの並び方[シーケンス]、分子量分布、組成のグラデーションなど)を特定できず、マテリアル・ゲノムを使った材料設計は使えないことになります。
そこで、重合シミュレータが必要になります。
重合シミュレータ、POSEIDON
POSEIDONとはPolymer Sequence Identify on Webの略で、ブラウザー上でラジカル重合のシーケンスを解析する、筆者が作成したソフトウエアーです。
これまでにBASIC, C, C++, Javaと開発言語は変遷してきたが、現在はHTML5+JavaScriptのプログラムで動いています。
詳しいことは私のWebページ、ポリマー編を参照してください。
実際にポリマー・シーケンス(モノマーの並び方)を次のPOSEIDONで計算してみてください。
プルダウン・メニューからモノマーの種類を(2種類以上)選択してCalc.ボタンを押すとポリマーのシーケンス(モノマーの並び順)を計算します。(Proバージョンでは汎用モノマーが自由に使え、重合度を管理でき、それ以外の便利な機能も搭載されています。)
機能を簡単に説明します。
各モノマーの反応性比をQ-e値から計算します。
初期濃度からポリマー末端がどのモノマーと反応するかの付加確率を算出します。
サイコロを振って確率に従ってどのモノマーが次に反応するかを決めます。
うっかりしていました。
このPoseidonにはエチレン モノマーが入っていませんでした。
(公開して2年以上経っているのに誰も指摘してくれないのですね。)
例えば、エチレン(A)/酢酸ビニル(B)=50/50molでは
BABBBAABBBBABBABABABABBBBABBABBABBABABBBBAA
BBAAABABAABAAABBBABABABABBAABAAABBBBBABABAB
AAABBAABBBBABBABBAAAABABABBABAABAAABAAABBAB
BAABBAABBABBBAB
このようなイメージの高分子が生成されます。
醋酸ビニルの方がより多くポリマーに導入されます。
(この後はPro版のみの機能)
次に消費された分、新しいモノマー比率でシミュレーションを行います。指定した重合率までこの操作を繰り返します。
重合率が98%ぐらいになると、残っているエチレンの比率が高くなるため、ポリマー中に導入されるエチレンの量が多くなります。
BBBAABAAAAAAABBBABAABAABBABBAAABAABABBAAA
BBAAABBBBBAAABABAABBABABAABAABAAAABAAAAAB
ABBAABAABAAAABAAAAAABBAAABABAABABABAABBBA
AAABAABABAAAABABABABABAA
こうしたシーケンス(並び方)を解析します。
例えば、ポリマー中のA-A連鎖, A-B連鎖, B-B連鎖の比率を算出する。(Pro版のみの機能)
こうした情報を併用することで、マテリアルズ・インフォマティクスを行っていきます。
フッ素ゴム系のパッキンの主骨格設計
ビニリデンフルオライド(VDF: CH2=CF2)系のフッ素ゴムは耐熱性、耐油性、耐薬品性が高く、自動車、航空機、化学プラントなどで広く使われています。
2元系のポリマーとしては、VDF-HFP(ヘキサフルオロプロピレン)、3元系のポリマーとしては、VDF-HFP-TFE(テトラフルオロエチレン)などが商品化されています。
2元系のVDF-HFPでは、フッ素含量が70%のものが使われています。
VDFのフッ素含量は水素に対して50%、HFPのフッ素含量は100%なので、VDFの比率をXとすれば、次式が成立します。
H:F=2X : 2X+6(1-X) =30:70
そこで、ポリマー中に69.2%VDFが導入された共重合体を合成すればフッ素含量が70%となる。
それであれば、モノマー比率VDF:HFPを69.2:30.8で重合すれば良いかというと、それほど簡単ではありません。
目的とするフッ素含有量のポリマーを製造には,どのようにすればいいでしょうか?
Materials Infrastructureの問題を解こう。
HFPの反応性は非常に低いため、69.2:30.8で重合してもポリマー中のVDFの導入量は90%近くになってしまい、フッ素含量は低下してしまいます(下図参照)。
実際にVDFの仕込み組成を変化させて重合を行ない、VDFのポリマー中の導入量を検討した論文がありました。(Journal of Fluorine Chemistry 126 (2005) 577–585)
このような実験結果があった場合には、作図法から、70%VDFをポリマーに導入したいのであれば、VDFの仕込み量は40%と簡単に求めることができます。
コンピュータの最も苦手とする解析方法でしょう。
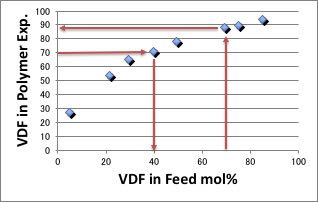
VDF:HFP=40:60で重合した時に、ポリマー中に70%VDFが導入されると言うことは、ただでさえ少ないVDFは速やかに消費されると言うことになります。
そこで、こうした系で重合を行う場合には、40:60の比率を保つためにVDFを連続的に補いながら重合を行うか、重合をあるところで止めモノマーを回収再利用する必要があります。
こうした設計の問題点は、
- VDF-HFP-TFEのような3元系についても,こうした実験結果が揃っているか?
- CTFE(クロロトリフルオロエチレン)、PFP(ペンタフルオロプロピレン)、PFMVE(パーフルオロメチルビニルエーテル)など、フッ素ゴムで利用されるモノマーの実験結果が揃っているか?
が問題になります。
当然、フッ素ゴムを商業化している企業はそうしたデータを持っているでしょうが、企業秘密としてオープンにはしていないでしょう。
これまでは、こうした隠されたデータにより、経験の無い企業はその分野に参入しにくいという障壁がありました。
ところがMaterials Informatics が進み、Poseidonのようなソフトが整備されてくると、コンピュータだけで、こうしたポリマーを設計できてしまいます。
そこで「モノづくり日本」の牙城が崩れると、急に騒ぎ出しているようです。
(とは言っても、世界最先端のフッ素ゴムの製造会社はDu Pontや3M、Montefluosで、日本の牙城ではありませんが、逆にそうした会社に”追いつけ追い越せ”をしたいなら取り入れたい技術であるは確かでしょう。)
POSEIDONによる重合シミュレーション
それでは、POSEIDONを使って、ポリマー中にこれらのモノマーがどのように導入されるか検討してみましょう。
授業で伝えたURLにアクセスしてPOSEIDON miniを立ち上げましょう。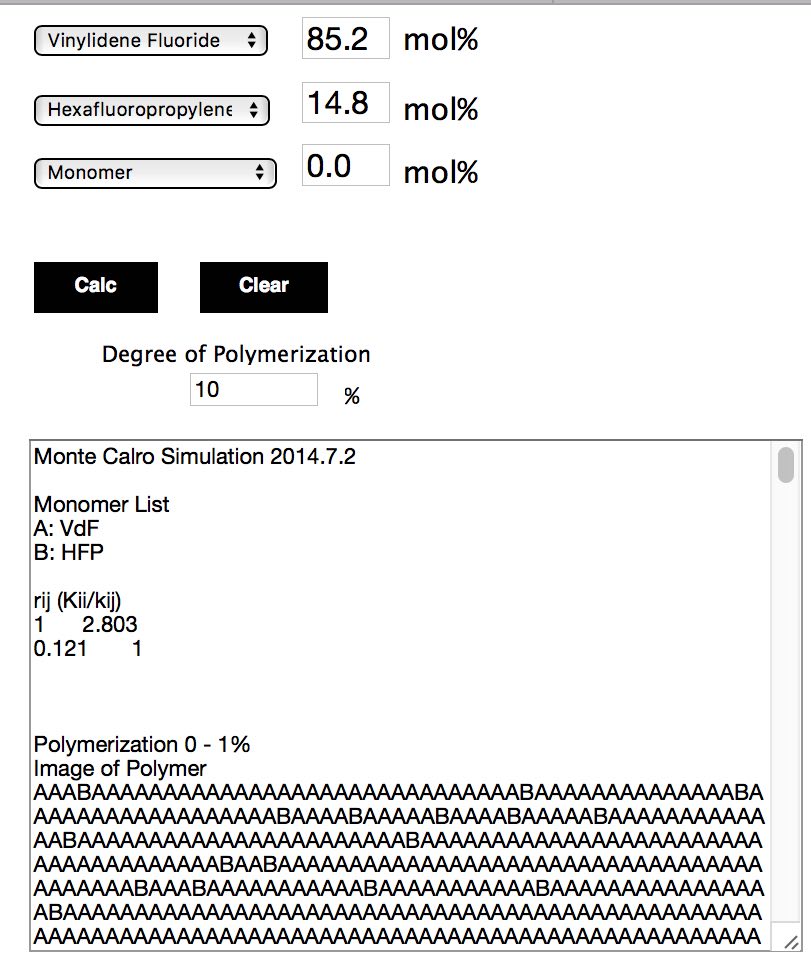
重合率は10%として、モノマーの比率を変化させながら、ポリマーに導入されるモノマーの比率を計算します。重合シミュレーション結果のサマリーから、10%重合時のポリマー中のVDFの量の平均を求めます。
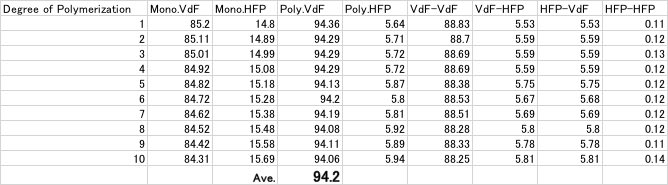
全ての実験値の仕込み比率に対する重合シミュレータの結果をテーブルに加えると以下のテーブルが得られます。
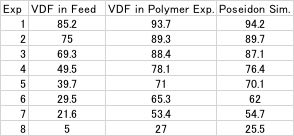
非常に高い精度で、シミュレーションだけからVDFのポリマーへの導入量が計算できることがわかります。
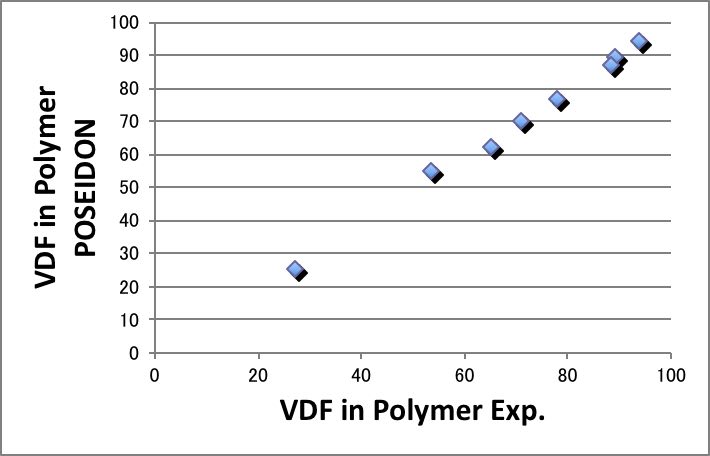
つまり、実験することなしに、シミュレーションだけで、モノマー比率VDF:HFP=40:60で重合すれば、フッ素含量70%のVDF-HFPのフッ素ゴムが得られるとわかります。
こうした共重合組成を決める遺伝子=GenomeはモノマーのQ-e値であることが理解できるでしょう。
そして、それをVDF-HFP-TFEの3元系や他のモノマーに適用するのがいかに簡単かも理解できるでしょう。
3元系ポリマーの設計
VDF-HFPのパッキンは、エタノール混合のガソリンで大きく膨潤してしまう問題点が明らかになりました。
化石燃料と異なり、エタノールは再生可能な自然エネルギーとして注目されています。
(食料であるトウモロコシから発酵法で作っていると言う問題点はありますが、ここではその議論には触れません。)
エタノールの含有量に従って、E3ガソリン、E10ガソリンなどとして検討が行われましたが、そうしたガソリンがフッ素ゴムを大きく膨潤させてしまいます。
そこで、フッ素含有量をアップした73%のVDF-HFP-TFEの3元系フッ素ゴムが開発されました。この3元系のフッ素ゴムがゴムになる条件が知られています。(フッ素樹脂ハンドブックより)
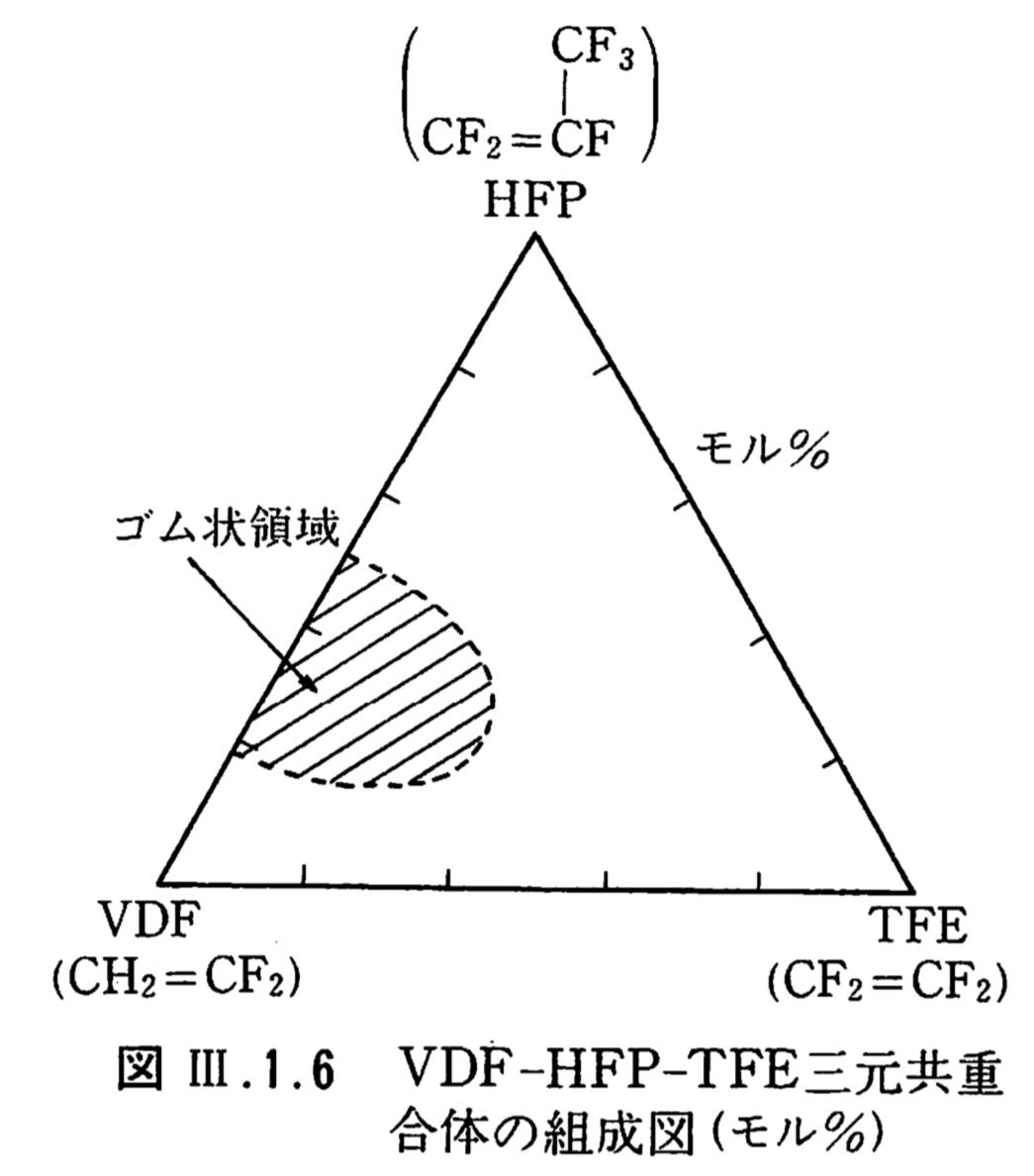
ゴム領域になる条件から
VdF 40-80% 1-(x+y)
HFP 20-50% y
TFE 0-40% x
フッ素含量73%
2*(1-x-y) : 2*(1-x-y)+6y+4x= 27:73
変数が2つで式が1つなので組成は厳密には求まりません。
しかし、VDF:HFP=40:60で70%になることは判っています。
TFEは水素を持たないので、ポリマーに導入されればフッ素含量は高くなります。
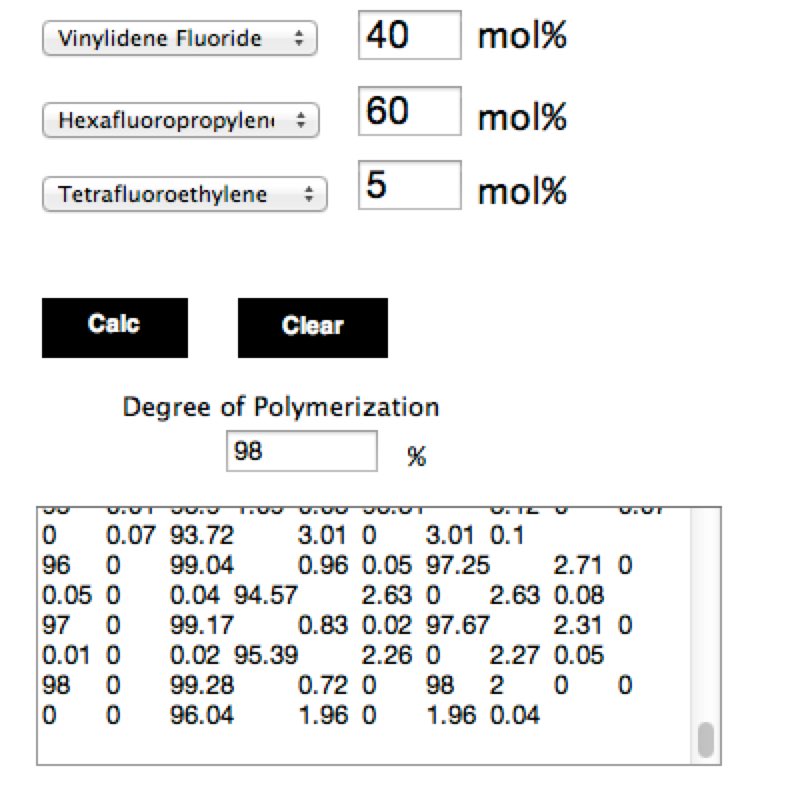
そこで、TFEの仕込み量を適当に設定してシミュレーションを行ってみます。
(トータルは100でなくても良い。内部的に補正します。)
重合によってモノマー比率は変わっていく。
仕込み比率VDF:HFP:TFE=23.7:72.5:3.7の時にポリマー中に、VDF(A):HFP(B):TFE(C)=56:37.9:6.1導入されフッ素含量は73%のポリマーになる事がわかります。
ポリマーのイメージとしては次のようになりました。
BAAAABAABABBBABBABAABABBAABBBAABABBAABA
BABBBBABABABBABBABBAAABBABABABABABAACBA
ABBAAAAAAACBBABAABABAAAAABABAAAABBABBBB
BBBAABBAAABAAAAABAAABABBABABABBB
特徴としてはHFP(B)連鎖が非常に多くなる事です。
HFPは単独重合しにくいモノマーなので(M1:VDF,M2:HFPで反応性比r1=5,r2=0)このようなポリマーは合成できません。
そこで他の方法を検討します。
TFEのポリマー中の含有量(X)を1-40%の1%刻みと仮定して、HFPのポリマー中の含有量(Y)を決めます。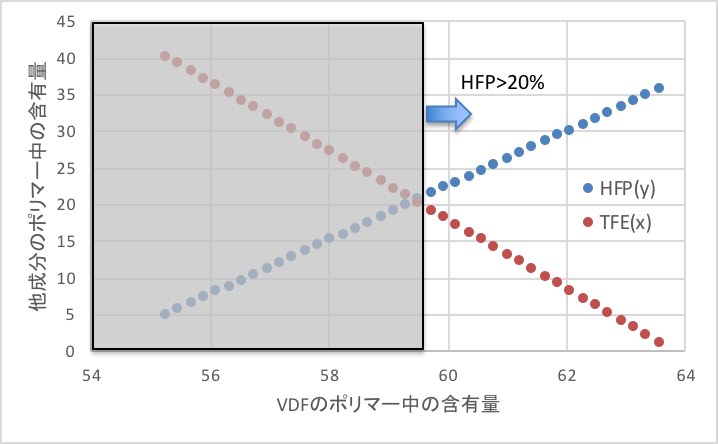
フッ素含有量が73%となる処方は上図のように表現されます。
ポリマーがゴム領域になるには、HFPのポリマー中の含有量は20%以上である必要があります。
そこで、図中の右半分が候補組成になる。HFPは重合しにくいモノマーなので、HFPの導入量は少ない方が合成しやすくなります。
そこで、ポリマー中の比率はVDF:HFP:TFE=59.5:20.5:20を目指す事にします。
POSEIDONを用いて、原料の仕込みを検討すると、VDF:HFP:TFE=25:38:11.6の時に、ポリマー中に、VDF:HFP:TFE=59.2:20.56:20.22導入される事がわかります。
その時のポリマーのイメージは次のようになります。
AAAACAACACACACABABAAAAAAABAACBAABACACB
AAAACBAAABBABABBABCAACABABBABAAABAAABAC
CAACABAAACAAABACABAABCAACBAAABAACACAACA
BAAAAACABACACCACACACACABABBCACA
同じフッ素含量が73%でも、先ほどのイメージとは非常に異なりHFP(B)連鎖も少なくなる事がわかると思います。
この仕込み組成を探索するのは、グラフ法はあまり有効ではありません。
この違いを表現する遺伝子は、ポリマー中のシーケンスを解析した、ダイアッド(2連鎖の割合)、トリアッド(3連鎖の割合)です。
POSEIDON miniではダイアッドの結果を出力します。
Diad %
A-A: 28.19% A-B:15.27% A-C:15.76%
B-A: 15.32% B-B:2.85% B-C:2.39%
C-A: 15.71% C-B:2.44% C-C:2.07%
A-B,B-A連鎖、A-C,C-A連鎖、B-C,C-A連鎖は同じものなので,足したものがポリマー中の割合になります。
この割合が変化すると、(例え、ポリマー中に導入されたモノマーの比率が同じでも)物性によっては値が大きく変化します。
これはランダム・ポリマー、完全交互共重合ポリマー、ブロックポリマーの違いを表現する遺伝子として非常に重宝します。
この遺伝子の使い方については別途説明します。
シーケンス解析とポリマー物性
ここでは、HFPのポリマー中への導入量が最小(20.5%)になるように設計しましたが、フッ素ゴムとしての性質は十分ででしょうか? (Materials Informaticsの問題)
ゴムの重要な性質として、耐寒性が挙げられます。低温になるにつれ、ゴムは弾性を失い、パッキンとしての性能が低下します。
宇宙、航空機用のパッキン、寒冷地で使う自動車用のパッキンで問題になります。
このゴム弾性を失う温度と、ポリマーのガラス転移温度(Tg点)は密接な関係があります。
そこで、VDF-HFP2元系、VDF−HFP-TFE3元系のポリマーのTg点を予測してみましょう。
データはフッ素樹脂ハンドブックから収集しました。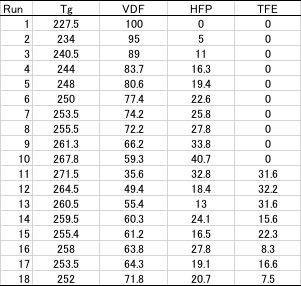
このテーブルを解析すると通常の重回帰計算で十分な精度でTg点を予測できる事が下図からわかります。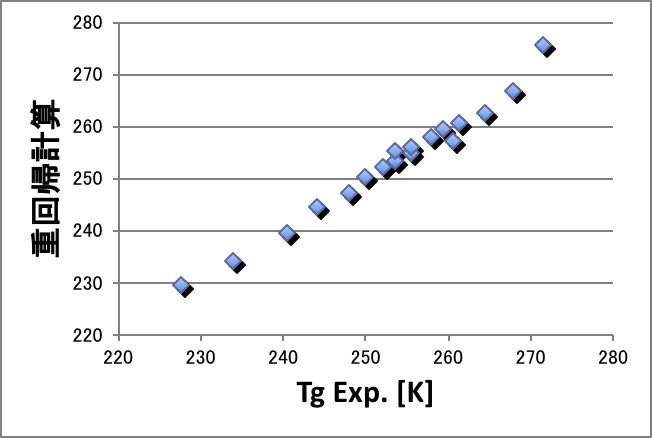
自分で得られた回帰式を書き下しておきましょう。
Tg[K]= AVDF + BHFP + C*HFP +D
このA,B,Cを比較することで、Tg点を下げるにはどの成分を上げ下げすれば良いかが明確にわかります。また、A,B,Cが大きく変わらないことから、ダイアッドまで考慮しなくてもTgの計算値は精度が高いと言えます。(A,B,Cが大きく異なる場合には2連鎖の情報を加えないと精度が出なくなります。)
先ほどのHFPが20%以上の組成で,候補に上がったポリマーのTg点を予測してみましょう。
VDF:HFP:TFE=59.2:20.56:20.22と言うポリマーのTg点がどのような位置付けにあるのか、自分で確認してみましょう。
このように、ポリマー中に導入されるフッ素量が計算でき、その組成でのTg点が計算できるなら、2つの指標で組成比探索が可能になります。その場合は、別の章で説明した遺伝的アルゴリズム(GA)とPOSEIDONを組み合わせて、探索してしまうのが有効です。
Q-e値の算出
ポリマー中のシーケンスを決める遺伝子はQ値、e値であると説明しました。それでは、Q値、e値が求まっていないモノマーを用いて、マテリアル・ジーノムをするにはどうしたら良いでしょうか?これは、モノマーの持つ情報を解き明かすことになるので、Materials Informaticsの問題になります。
ラジカル共重合のシーケンスを決めるは、本来は実験値の反応性比r1, r2です。反応定数をKijとした時に、反応の素反応は次のように書くことができます。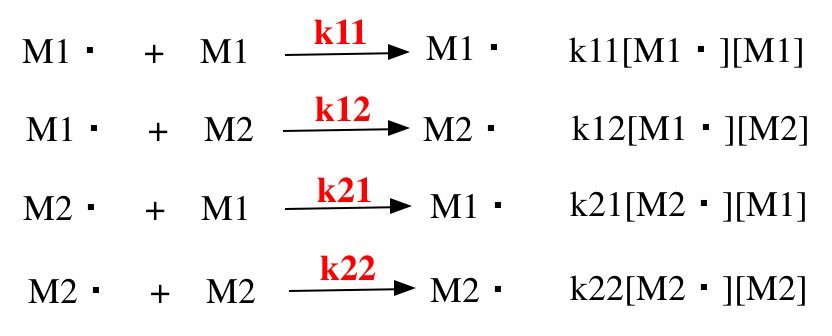
反応性比は次のように求まる。
r1=k11/k12
r2=k22/k21
実験的には、モノマーの濃度が大きく変わらない重合初期に反応を止め、ポリマー中のモノマー1、モノマー2の割合をNMRや元素分析で決定します。
通常は仕込み組成を何点か変えて実験を行い, Mayo-lewis法やFineman-Ross法でr1やr2を決定します。
本来は、モノマー・ペアごとに値が決定されるパラメータで、多くのr1, r2が例えばPolymer Handbookに記載されています。
分子軌道計算で行うのであれば、上述の4つの素反応に関して、遷移状態を計算し、反応速度定数を求めます。
ただし、かなり高い基底関数を用いて計算しなくてはオーダーすら合いません。
しかも、気相反応ならともかく、液相反応では誘電率の問題があるので,極性モノマーでは合わないと考えたほうが良いです。
このr1, r2をモノマーのQ値、e値で表すことができるとしたのがAlfrey-Price です。スチレンのQ値=1.00, e値= -0.80として、様々なモノマーのQ値、e値が決定され、ハンドブック等に記載されています。
基礎式は以下のようになります。
r1=Q1/Q2 ・exp -e1(e1-e2)
r2=Q2/Q1 ・exp -e2(e2-e1)
これを解くと、Q値とe値の組みは2つ求まります。
どちらを採用するかは研究者によってまちまちのようです。
また、モノマーによってはスチレンと共重合しないことがあります。
その場合、スチレンと共重合し、かつ対象のモノマーとも共重合する第3のモノマーのQ値e値から対象のモノマーのQ値e値を決定していきます。
そこで曖昧性が高くなってしまいます。
フッ素系のモノマーの場合は、テトラフルオロエチレンを基本にする事が多いようです。
また、完全交互共重合の場合、r2=0になり、Q2=0となる。するとr1の計算で、Q1/Q2がQ1/0でエラーになりますので、完全交互共重合は表現できません。
このような事もあり、様々なハンドブックにあるQe値を収集すると大きなばらつきがあることがわかります。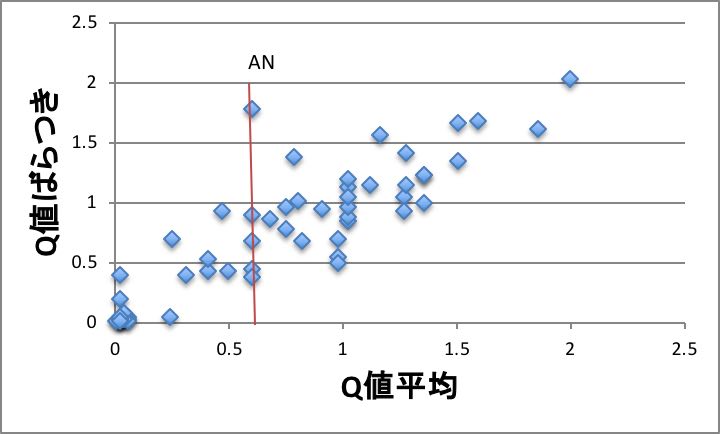
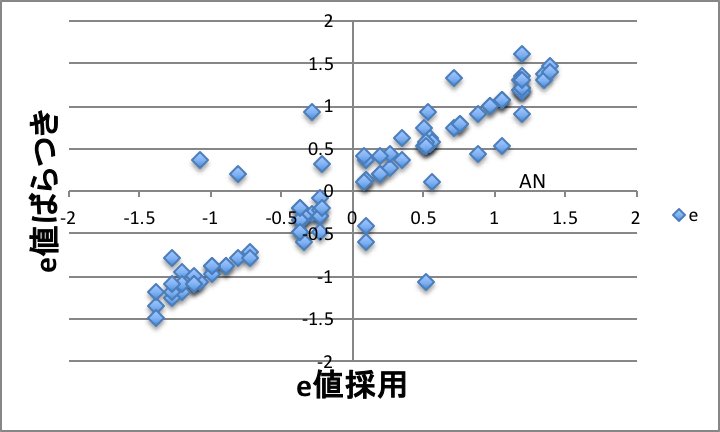
横軸は収集された、あるモノマーのQ値の平均、筆者が採用したe値で、縦軸は収集されたQ値,e値のばらつきになります。
例えば、アクリロニトリル(AN)のQ値では0.37から1.78になります。e値では0.9から1.6になります。
e値に関してはモノマーのTailの炭素上の電荷と相関があるので、モノマーを分子軌道計算して電荷を得れば、どれを採用するか絞り込むのは容易です。しかし、Q値に関してはどれを採用するかは難しい問題となります。
Q-e値の推算
本来知りたいのは、r1,r2ですが、それをモノマー構造のみから知るのは難しいです。
Q値、e値をモノマーの特性値とすることは本来できません。
つまり、モノマーのペア次第でQ値、e値は変動してしまいます。
そのような問題点があるのを承知の上で、モノマーの特性値としてのQe値を決定する方法を化学情報学的に作成しました。
井本稔のラジカル重合論によれば、ラジカルのSOMO、モノマーのHOMOと軌道混合がおこる。次にその時できた反結合性軌道がモノマーのLUMOと軌道混合をおこし重合が進むとあります。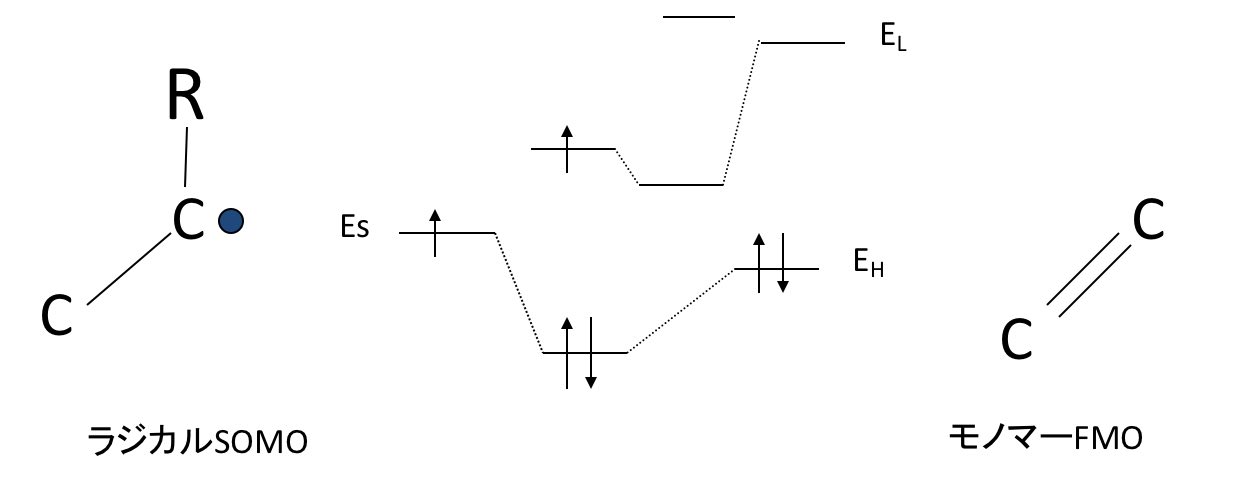
これに電荷相互作用とモノマーの大きさの項を取り入れたモデルを作成し、ニューラルネットワーク法で予測式を作成しました。Q値の様に、値がマイナスにはならないもの、最大と最小の差が100倍以上あるものは、値をlogをとって推算するのが一般的です。
軸がlogである事を考えるとお世辞にも精度の高い推算式とは呼べませんが、次のような予測式が得られました。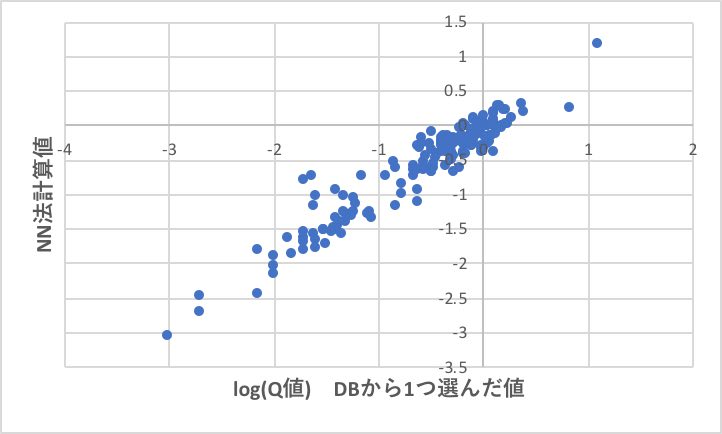
e値に関してはそれなりに収束しています。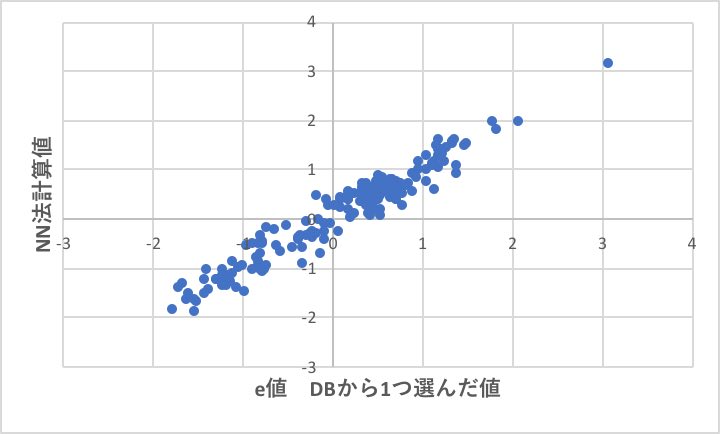
本来は、ここでデータのクレンジングをしなければなりません。
データベース中で計算値の値が合わないものを、他のQ-eペアが無いかを検索します。
これは結構大変な作業になります。
Q値が合うデータを採用しようとするとe値が大きく外れる事がありうるからです。
しかも、精度が高くなったところで、シーケンス解析の精度が高くなるかは別問題です。
元々Qe値はモノマーのペアが決まり、重合方法なども決まった時に定まるもので、沸点や密度の様な物性値とは異なります。
ある程度の精度が出たところで検討を打ち切るのも重要な判断となります。
実はここで精度の出ていないことには、もう一つの理由があります。
手軽にQe値を得るためです。
もし非常に高精度な非経験的分子軌道法の計算結果を用いてNN法で予測式を組めば、もう少しよく収束するかもしれません。
しかし、その場合、新規なモノマーを計算しようとすると、その説明変数を得るために、やはり高精度な非経験的分子軌道法で計算しなくてはならなくなります。
それよりは、モノマーの3次元構造を入れるだけで、おおよそのQe値を計算してくれる方がユーザーとしてはありがたいのです。
下図はJavaScriptで書いたWebAppです。
半経験的分子軌道法のMOPACで構造最適化した構造を入力すれば、Qe値を計算します。
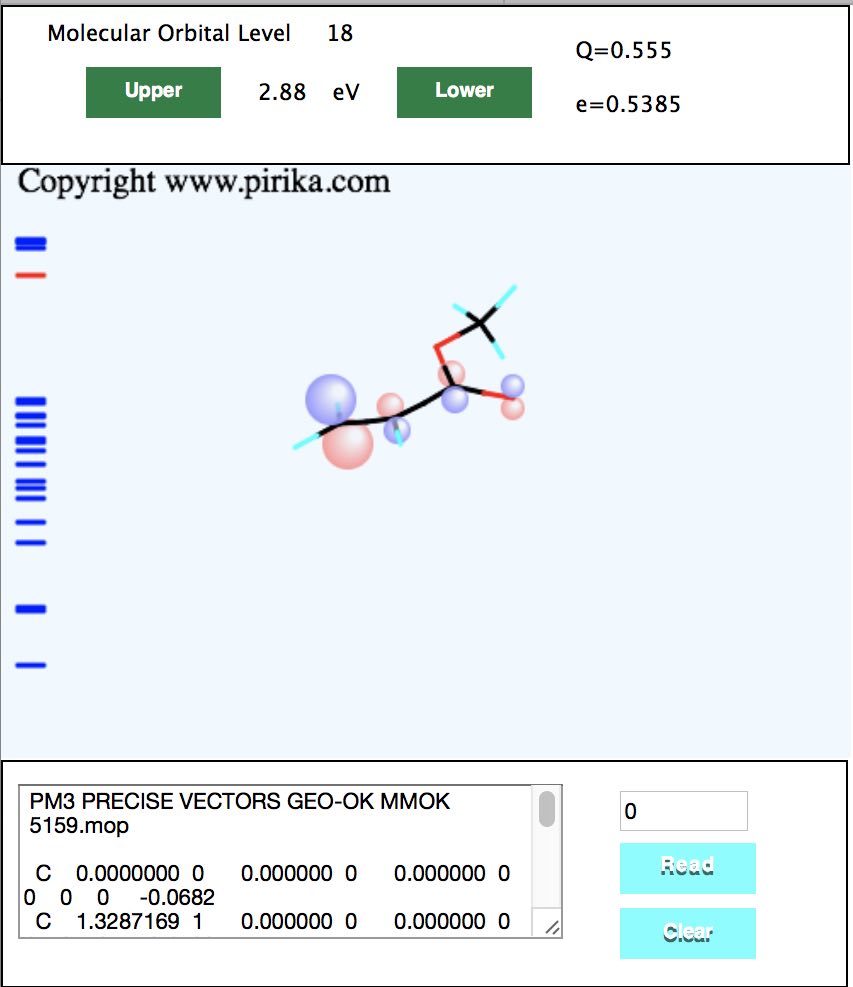
ブラウザー上で動作するので、マシンを選ばず、iPhoneの上でも十分高速に動作します。
内部的には3次元の分子構造からCNDO/2で分子軌道を計算し、その計算結果などからNNでQe値を計算します。
3次元の分子構造はフリーウエアーでも簡単に組めますし、フォーマットを変換するのにはOpen Babelを使えば簡単に行えます。簡単な操作で取り敢えずQe値を得て、POSEIDONを使ってシーケンス解析を行う事ができるのは大事なメリットです。
Poseidon Proには実験結果を解析して最適なQe値を定める機能が搭載されています。
そこで、取り敢えず推算値を信じて実験を行い、結果がでたら、それをシミュレータにフィードバックする事ができます。

結果をフィードバックすると、本来のQe値の意味は失われます。単に遺伝的アルゴリズムを用いて、一番精度よく実験結果を表現するQe値を決めるので、そのペア、重合条件に一番よく合い、POSEIDONで解析するのに一番適したQe値となります。
つまりQe値が未知のモノマーに関しては,次のように取り扱います。
初期値をモノマー構造からNN法で推算する。
実験がスタートしたら,その実験結果から,POSEIDONのシミュレーションが実験にあった結果を与えるように,Qe値を最適化させて行く。
企業ユーザー
こうした、独自のツール(元はPOSEIDONでも、自社用に進化させたツール)を育てて行くのが大事なのでしょう。
多くの企業では「手っ取り早く、ソフトを購入して」と考えるようですが、そうしたソフトから出て来る結果は、購入した企業全てが等しく享受できます。
MOの計算結果はどの企業が行っても同じになります。
育てられたツールは、その育ての親のニーズに答えてくれるソフトに進化して行きます。
手抜きをすれば、結果は自分に跳ね返って来ます。
しかし現実問題として企業でゼロベースでソフトを開発するのは無理があるでしょう。
既存のデータアセットに自社のデータを継ぎ足して再学習させるだけで自社の取り扱いたいモノマーに特化したQe値、そのQe値を使ったポリマーシーケンスを利用できるようにしていく。
そのベースとなる部分にPOSEIDONを使えば良いのです。
雑感
ガラスや触媒などと異なり,ポリマーの設計にはポリマー特有の難しさ,“モノマー単位の量子化ベルト問題”があります。
ちなみに、筆者は自分の持つ蔵書700冊を自炊してデジタル化しました。そのうちの10%、70冊は高分子関係の書籍でした。
コンピュータ関連の書籍は新しいものを取っておけば古いものは処分してしまいます。
しかし、高分子関係の書籍は、1960年代の書籍であれ、未だに「なるほど」という気づきを与えてくれます。
新しい書籍、論文だけを読んでいれば良いものではありません。
材料(高分子複合体)、膜、塗料、接着剤なども別に100冊近い書籍を所有しています。
そうした,これまでの知識、経験をコンピュータ上に構築して行くのは大変な作業となります。
新しいポリマーが年1000トン製造されることは非常に稀で,高機能,高付加価値のポリマーを少量・多品種製造しなければならない時代になっています。
もしくは,他社と差別化するためのチューニング技術が大事になっています。
それを行うためには,過去の経験に基づくだけではスピードが足りません。
情報学を駆使して開発のスピードを上げなくてはなりません。
ところが,現実問題としては,それをやろうとした時の,人材とツールが不足しています。
化学系のデジタル人材を育成という話もあります。
しかし,これも,MOやMDなど,いわゆる計算機科学用のソフトを利用できる人材、もしくは数理統計が行える人材の育成に留まっているように思えます。
MOやMDは使えるに越したことはありません。ただ現状でもMOやMDのソフトを使える人材は多くいます。そこから情報を取り出し、処理できる人材が足りないのだと思います。
化学情報系のデジタル人材の育成に関しては,教えられる教師が限られる,ツールが限られる,育成の場が限られるなどの限界があります。
一つの解決策としては,こうしたネット空間を利用して,時間,距離,コストの問題を飛び越えてしまうことでしょう。それにしても,ネット空間を有効に活用できる教師が少ないのも事実ですが。。。。
筆者は大学の時から合成系の高分子屋でした。
重合は結構時間がかかり,暇な時間が多い。
そうした時には特許や論文を読むものでしたが,物好きにも当時発売されたばかりのPC-8801を買い込んでプログラムの作成に夢中になりました。
コンピュータは化学を変える。
そうしたワクワク感を30年間以上持ち続けてきた訳ですが,振り返ると化学はあまり変わっていないようにも思えます。
一つだけ言えることがあります。AIやMG, MIなど流行り言葉に惑わされてはなりません。
この化学系AIブームで残るのは制御系ぐらい(工場の運転の合理化)では無いかと思っています。
ブームが去った後,本来人間の研究者として身につけておかなければならない知識や経験(特に失敗の経験)が浅いとAIに仕事を取られる側に回ってしまうのだと思っています。
次回は,Materials Integration(材料複合化)に関して,フッ素ゴムの配合処方の研究を例に解説しましょう。
情報化学+教育 > MAGICIAN 養成講座 > 講義資料 > 第3a回ポリマー設計と重合シミュレータ -POSEIDON-
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
