2018.9.3
情報化学+教育 > MAGICIAN 養成講座 > 講義資料 > 第3b回ポリマーの配合処方設計
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
第3a回では、フッ素系ゴムを例題に、Materials InformaticsとMaterials Infrastructureを中心に解説を行いました。
最初はMaterials Integrationも一緒に書いてしまおうか思ったのですが、あまりに長くなるので分割することにしました。
材料の複合化と言った場合、従来の処方設計と、最新のコンピュータを用いた複合化設計と2種類あります。当然、Materials Integrationという時には、後者の複合化設計を指します。
しかし、従来の処方設計に対しても、マテリアルズ・インテグレーションは非常に有効です。
フッ素ゴム系のパッキンの配合設計
先回述べた方法で設計されたポリマーは生ゴムと呼ばれる。
この生ゴムに様々な副資材を配合して、混錬し、架橋させることによってゴムが得られる。
主な添加剤として受酸剤、充填剤、加硫剤、可塑剤と加工助剤が挙げられる。
受酸剤は加硫の時に生成する酸性物質を中和するために加えられ、主なものに、MgO, PbO, ZnO, CaO, Ca(OH)2がある。
充填剤としてはカーボンブラック、無機物のフィラーがある。
加硫剤としてはポリアミン、ポリオール、パーオキサイドなどの過酸化物がある。
可塑剤としてはDOP,PET、低分子量FKM、加工助剤としてはカルバナワックス、ポリエチレンなどがある。
多くの場合、生ゴムの製造メーカーが最終製品のパッキンまで製造することはなく、加工メーカーが生ゴムも含め資材を調達し、パッキンを作成する。
こうした原料は様々な資材メーカーが販売している商品なので、原料の詳しい諸元はわからない。
そうした商品名しか分からない資材を使って素材を設計して行くのにもMaterials Integrationは有効に使える。
まず、フッ素樹脂ハンドブックからデータを集め、テーブルを作成する。最後の4列が出来上がったゴムの物性値になる。
FKV種類からトリアジンまではゴムのシステム要件になる。
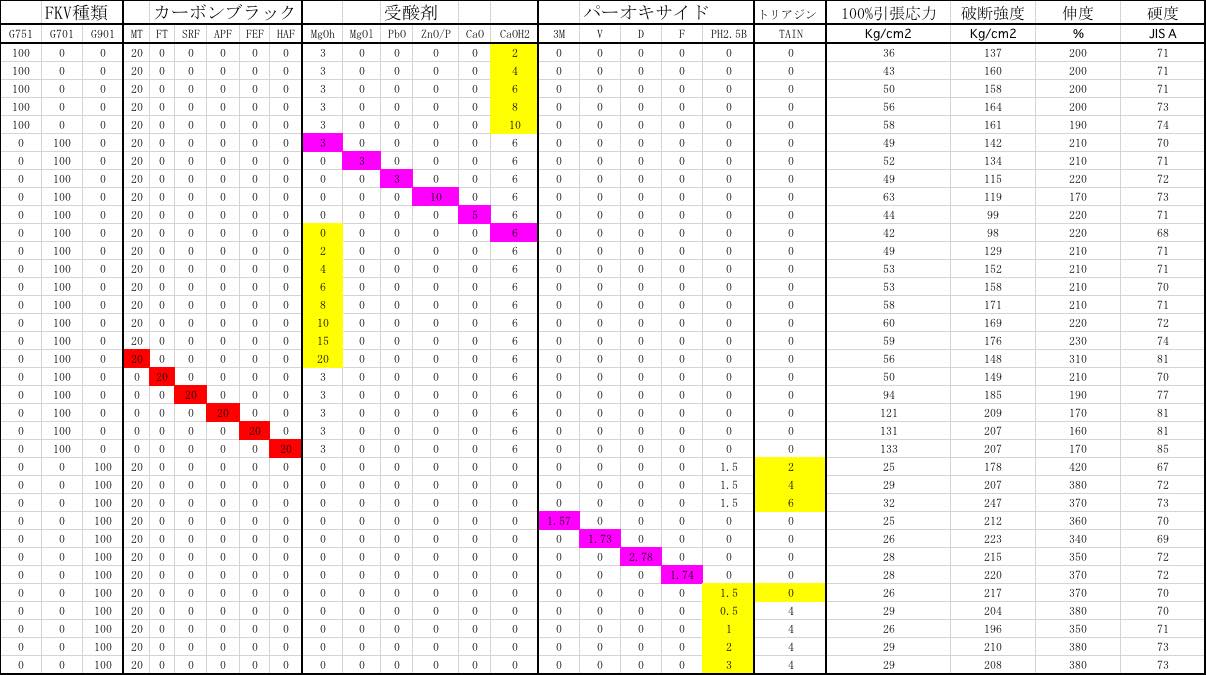
これは、目的変数が4つと説明変数が21、データ数が35ある場合の解析になる。
受酸剤、トリアジン以外は商品名で、その説明変数は加えた量だけがわかっている。
それが目的変数にどのような影響を与えているかがわかれば、4つの目的変数のうち3つを固定し、残りの1つの値だけを上げ下げしたいときにどのような処方を取ればいいかを計算で出すことができる。
それでは、4つの目的変数に対して、順番に重回帰法で予測式を作成しよう。ソフトウエアーは授業で配布したYSBを用いても、Excelに搭載されている重回帰分析でもどちらでも良い。
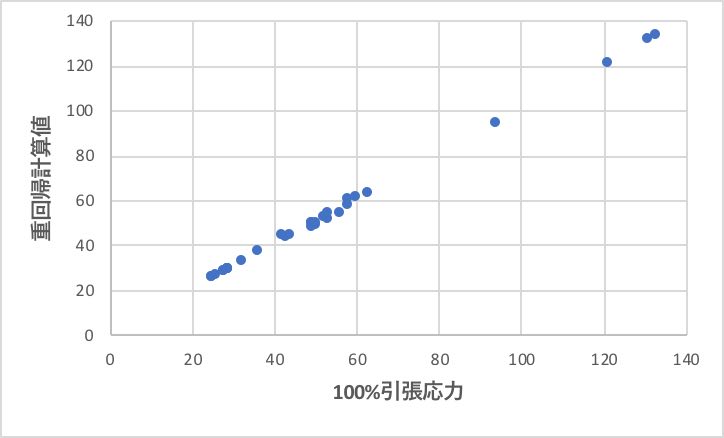
まず、100%引張応力を計算してみよう。
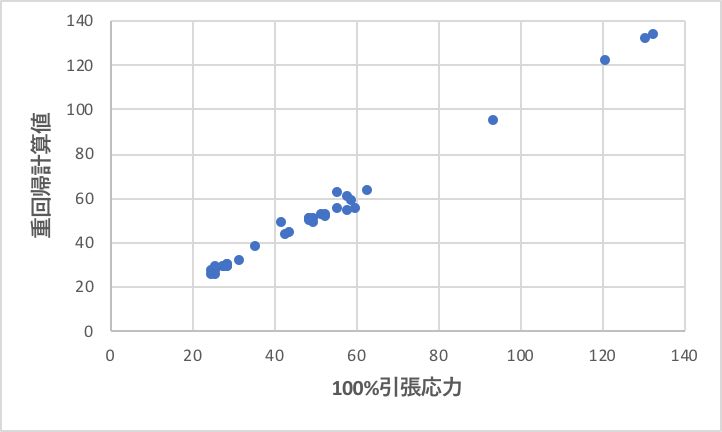
上図に示すように、ほぼ綺麗に100%引張応力が計算できていることがわかる。ここで作成された式の意味を確認しておこう。
100%引張応力=0.7462*G751+0.7629*G701+0.6917*G901 (生ゴム)-2.2666*MT-2.2584*FT-0.0592*SRF+1.2938*APF+1.7934*FEF+1.8920*HAF (カーボンブラック)+0.6610*MgOh+1.2573*MgOl+0.2573*PbO+1.4772*ZnO/P-0.8456*CaO+2.8500*CaOH2 (受酸剤)+0.7285*3M+1.2392*V+1.4906*D+2.3815*F+0.4526*PH2.5B (パーオキサイド)+1.0176*TAIN(トリアジン)+0.0156 (定数)
という式で表されていることが理解できるだろう。
生ゴムの種類としては、100%引張応力を一番高くするのは、G701,一番小さくするのはG901であることが係数を比較してみればわかる。
カーボンブラックの種類としては、MT, FT,SRFは100%引張応力を小さくし、APF,FEF,HAFはこの順に大きくする。
受酸剤はCaOのみ100%引張応力を小さくする。
パーオキサイドは全て100%引張応力を大きくするが、パーオキサイド-Fがその効果が最も高い。
従って、100%引張応力を一番大きくしたければ
G701/HAF/MgOl-CaOH2/F/TAIN系が良いことになる。
逆に一番小さくしたければ、G901/MT/CaO-CaOH2/系が良いことになる。
ただし、この式はあくまで、100%引張応力に関するもので、処方を変えれば、破断強度、伸度、硬度の値は変化し、また添加物の与える効果は、100%引張応力の時の効果とは当然異なる。
また、処方する時の量も考えに入れて置く必要がある。生ゴムの係数は大きくは違わないが、使用量は100部なので、影響は最も大きくなる。
(それを避けるためには、列を規格化してしまい、係数の大小を直接比べられるようにする。)
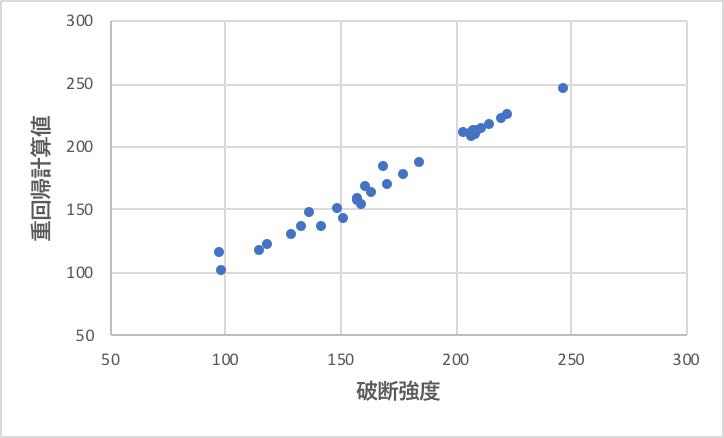
次に破断強度に関して、同じように重回帰分析をしてみよう。(伸度、硬度については自分でやってみよう)
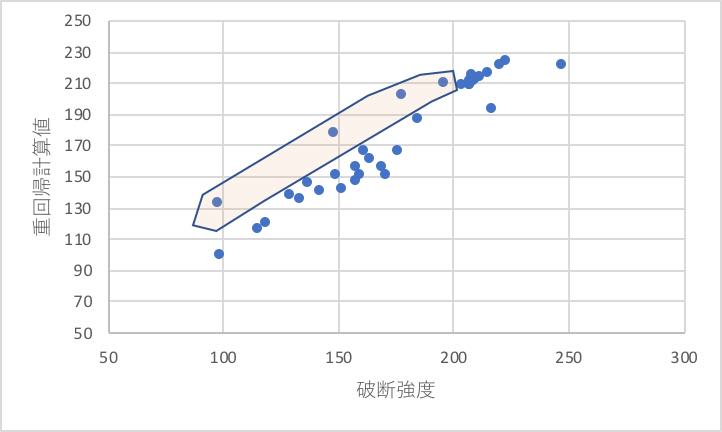
先ほどと異なり、少し精度が低くなる。
特に4系ほどメインの直線に平行で上にずれるデータがある。
重回帰分析では各説明変数の係数は固定の値になる。
ところが実際には、ある量を超えたら急に値が大きくなる(非線形性)、ある組み合わせの時に特異的に値が小さくなる(相互作用)ことがある。
そのような現象に対しては重回帰計算では精度が出なくなる。
それでは、どうしたらいいか?
非線形回帰のニューラルネットワーク法(NN法)を用いるのも手ではあるが、NN法は使いこなすのが非常に難しい技術である。
何故だろうか? このぐらいの非線形性であれば簡単に精度がアップされ、しかもそれが何故だかわからないからだ。
従ってNN法で予測されるものを作ってみても予想された性能が出ない。NN法で学習させ直して、を繰り返すことになる。
そして、ついに諦める。
つまり、この程度のデータ数で、予測性能が十分期待できるニューラルネットワークを構築するのは、それなりの知識と経験が必要だからだ。
慣れてくると比較的簡単にできるようになる。
どうしたら慣れることができるのだろうか?
データをよく見ることに尽きる。
合わないデータは実験誤差だろうと消去するようでは、化学系のデータサイエンティストは目指さないほうが良い。
データのクレンジング
それでは、先ほどの図で特定した4つのデータを、テーブルで特定しよう。RUN-11,18,24,33が相当する。
RUN-11,18はMgOhが関与する系、RUN-24,33はPH2.5BとTAINが関与する系であることがわかる。
さらに詳しく見て行こう。
受酸剤を用いる系は必ずCaOH2とそれ以外の受酸剤のペアで用いている。
そこで、テーブルの中でMgOhの量だけをふったRUNを抽出してサブセットのテーブルを作成する。
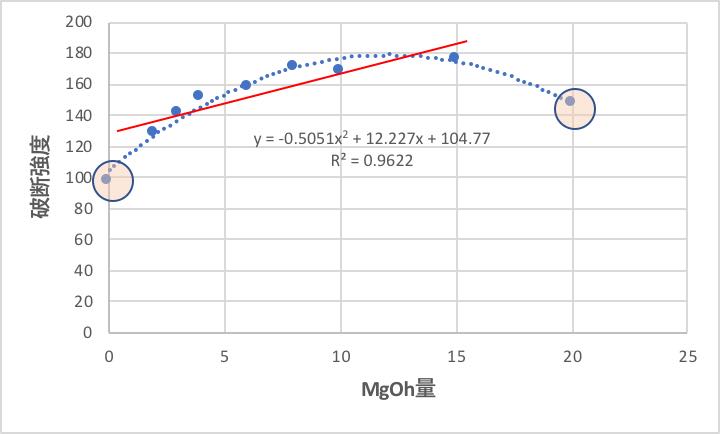
グラフ化して見ると明らかであるが、RUN-11は左端,RUN-18は右端の処方になる。
重回帰解析では、結果は線形になる。
そこで他の受酸剤の系も含めると、図中の赤い線が、平均的に一番誤差が小さくなると解釈される。
しかし、実際は上に凸の2次関数になることがカーブフィットの結果からわかる。
従って非線形性を導入しなければ予測式の精度は上がらない。
しかし、このデータはMgOhの量以外は全て一定の時に成立しているので、単純に上に凸の2次関数を予測式に組み込むのは難しい。
取り敢えず破断強度予測式の,精度を上げるのにRUN-11,18を除外して精度を上げるか、他のものを除外するか選択が別れる。
そして最終的に出来上がる予測式のパーフォマンスも異なる。
その際に一番重要なのは、「実験を行っている研究者とよく相談すること」であろう。
その際に、予測式を合理的に説明するのは、データサイエンティストの責務になる。
一つの解釈を示そう。
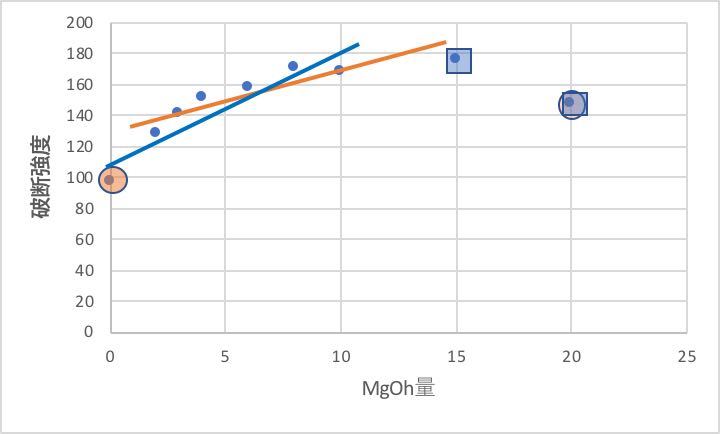
一番左と一番右を外した場合は、重回帰分析の結果になり、平均的には良くなる(赤い線)。
しかし、この場合は、一番右2つを外して考えるべきである(青い線)。
MgOhの量が変化した時の、他の物性をプロットすると次のグラフになる。
特に伸度について、一番右の点は、急に伸度が高くなっている。
つまり、MgOhの量が15を超えると、伸度が大きくなり、破断強度が低下する。ゴムとしてだらしないゴムになる。
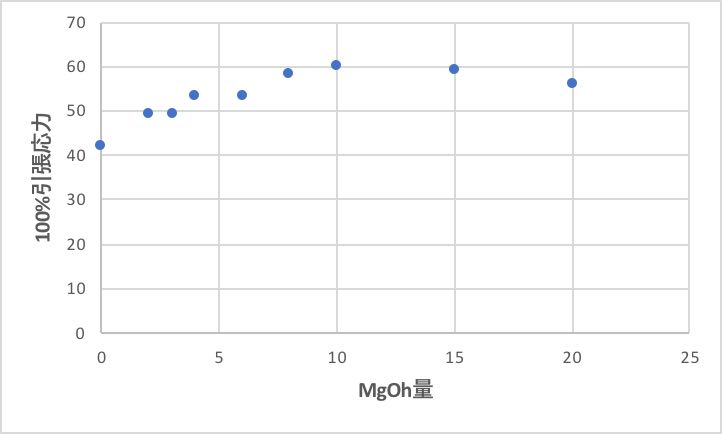
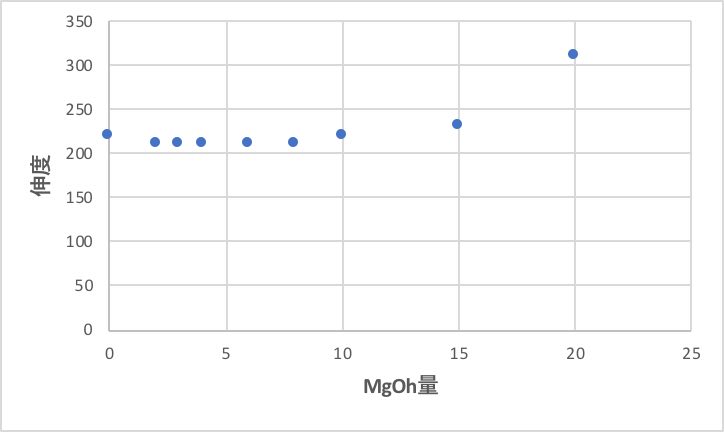
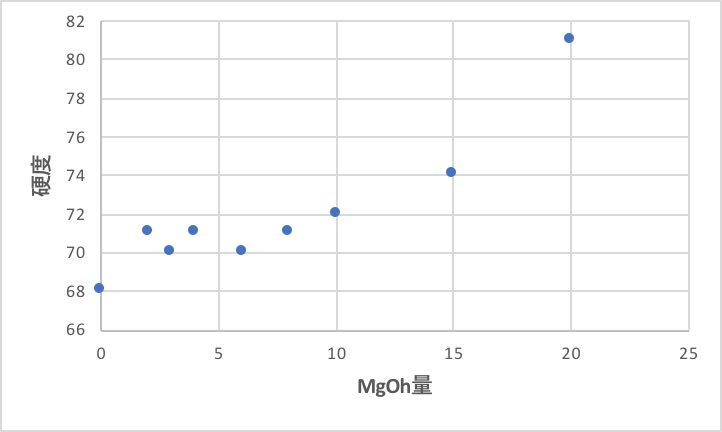
また、硬度や100%引張強度についても右の2つは異常値をとる。
そのような通常のゴムの特性を外れた領域を探索したいなら、右の二つは外せないが、通常のゴム領域で探索したいのであれば、右の二つは外すべきである。
ただし、通常のゴム領域を外れたものを探索したいなら、明らかにデータ不足なので、受酸剤量を大きくしたデータをもっと収得すべきである。
右の2つを外すのであれば、予測式としては受酸剤量が多いものに対しては予測できない。
こうした事を、実験系の研究者と打ち合わせるのである。
RUN-24,33のPH2.5BとTAINが関与する系については、自分で考えてみよう。
RUN-24,25,26,31を比較して見解を導いてみよう。
RUN-33,25,32,34,35を比較して見解を導いてみよう
ヒントはPH2.5BとTAINは両者をペアで使うもので、ペアでないものの取り扱いをどうするか?
もう一つのヒントは実験誤差の可能性だろう。
実験誤差を非線形性や相互作用に落とし込んで予測式を作成すると、多くの場合性能低下につながる。
非線形性を考慮するのは、データのクレンジング(第5回で説明)を行い、それでも必要であった解に留めたほうが良いだろう。
クレンジング後の予測式
筆者の理解で4つほどデータを除外して重回帰解析した結果を以下に示そう。
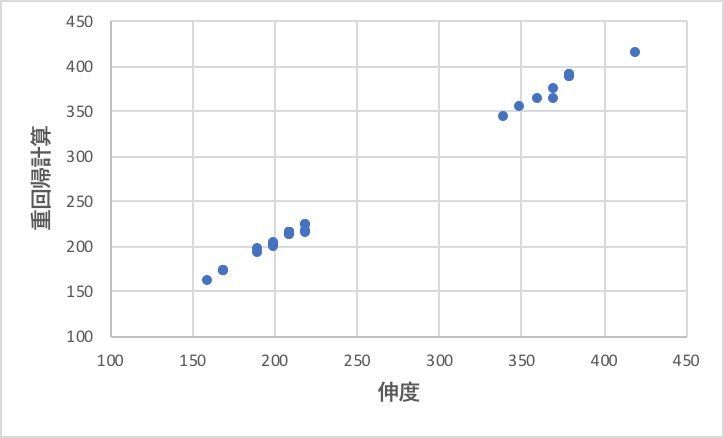
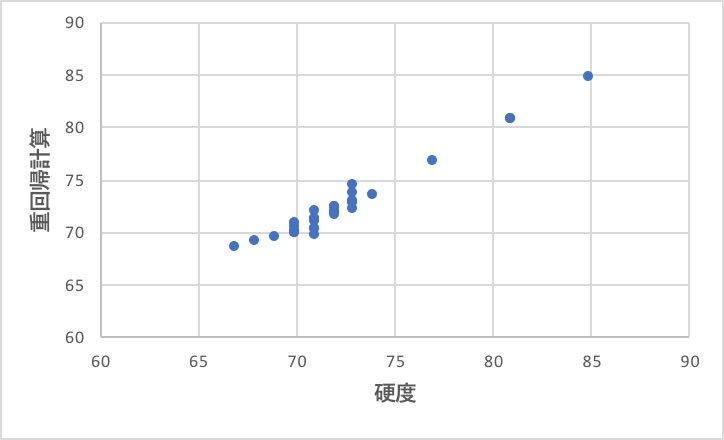
受酸剤の多い系には使えないが、非線形性を導入しなくても十分な精度で実験結果を再現できていることがわかるだろう。
逆に言えば、重回帰分析で精度の出る系をニューラルネットワーク法のような非線形回帰解析する事の無意味さも理解できるだろう。
今回の場合は、生ゴムを2種類以上混合した系、カーボンブラックを混合した系、パーオキサイドを混合した系は無い。
(そうした系が増え、重回帰解析でどうしても精度が出なくなったら、その時にNN法を利用すれば良い。)
Excel計算機
ここまで出来上がると、Excel上に計算機が構築できる。
処方を入力すると、物性値を計算する。
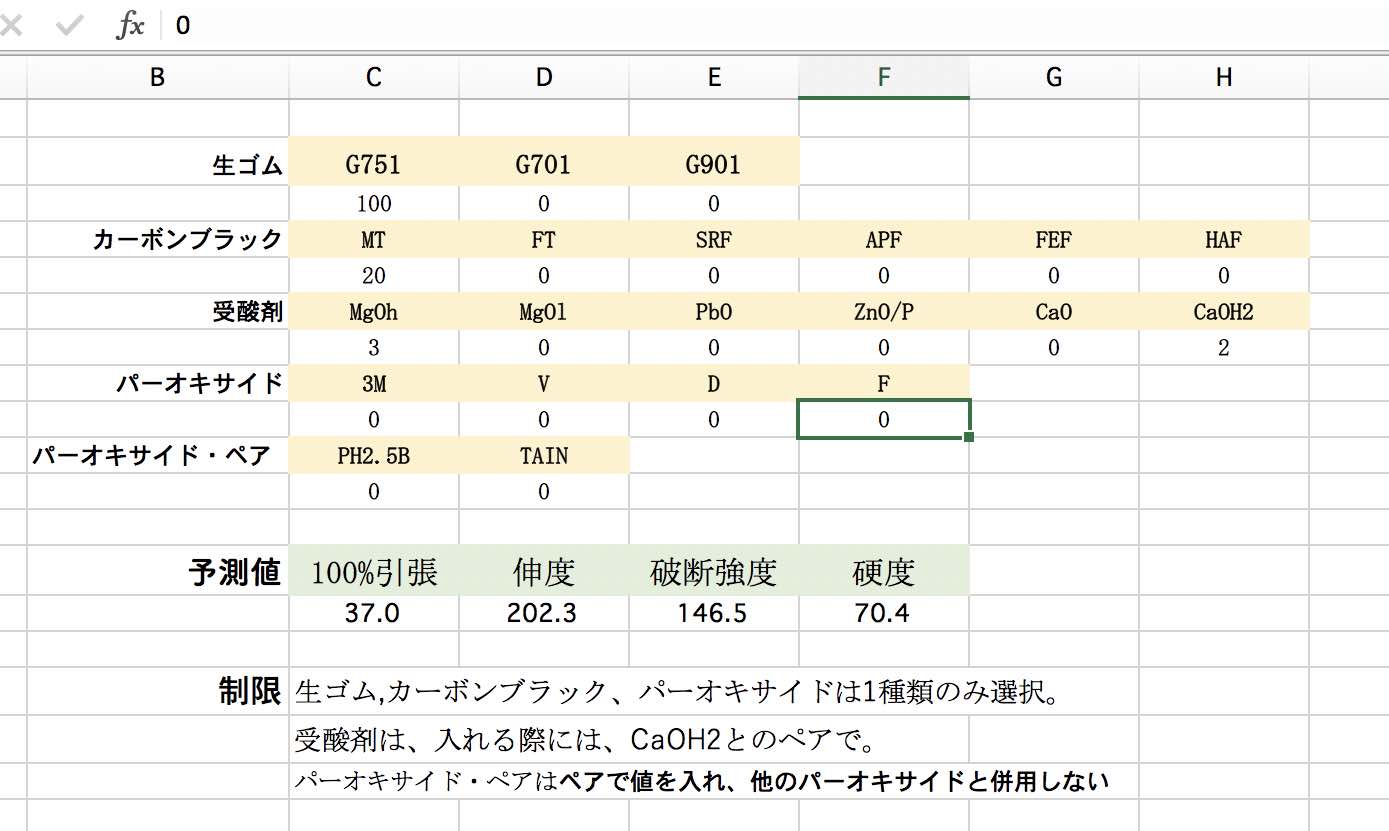
海外のメーカー品と比べ、自社の製品は(例えば)破断強度が足りない。
他の物性はそのままに、破断強度を10%だけ向上させるのに、処方をどういじるか?
エクセル上で処方をいろいろ検討して、一番よくなりそうなもので実際に実験を行う。
結果が予測値に合えば良いが、合わなければ予測式を再構築する。
この過程を素早く回せるかが一番重要になる。
各項目の重回帰係数が与えられているので、例えばカーボンブラックの種類を変えたら、各物性値がどう変わるかは理解しやすいだろう。
それにしても4つの目的変数を全て満足する処方を設計するのは大変かもしれない。
その際には、遺伝的アルゴリズムを用いて、自動探索してしまうのは一つの方法であろう。
そこまでやれば、胸を張って最新のMaterials Integrationと呼べるだろう。
制限事項をプログラムに反映させるのは少し手間かもしれないがチャレンジしてほしい。
自己組織化ニューラルネットワーク法
SOM(Self Organization Map)という解析方法がある。
これは定性的解析法として優れているので、授業でもよく取り上げている。
この方法を用いてフッ素ゴムの4つの物性を検討してみよう。
SOMのプログラムは所定のURLにアクセスして用いる。
まずは、下図のテーブルを用意する。
100%引張強度、破断強度、伸度、硬度を順にソートをかけて、データにL,M,Hのラベル付けをする。
そして、RUN-noも含め、24-L-M-H-Lの様に表現する。
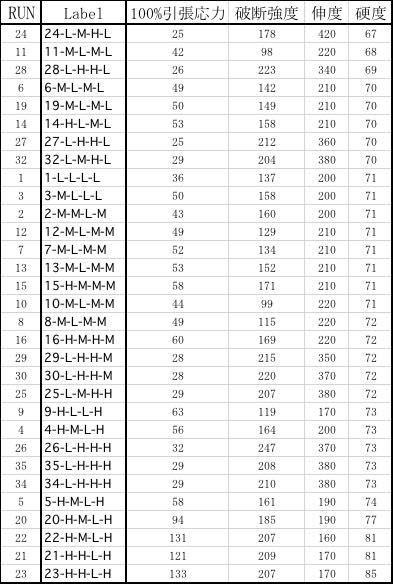
このテーブルをタイトル、RUN-Noまで全てコピーし、SOMのプログラムにペーストし、自己組織化させる。
つまり、100%引張強度、破断強度、伸度、硬度を4次元のベクトルとした時に、似たベクトルは似た2次元上の位置にマッピングさせてみる。
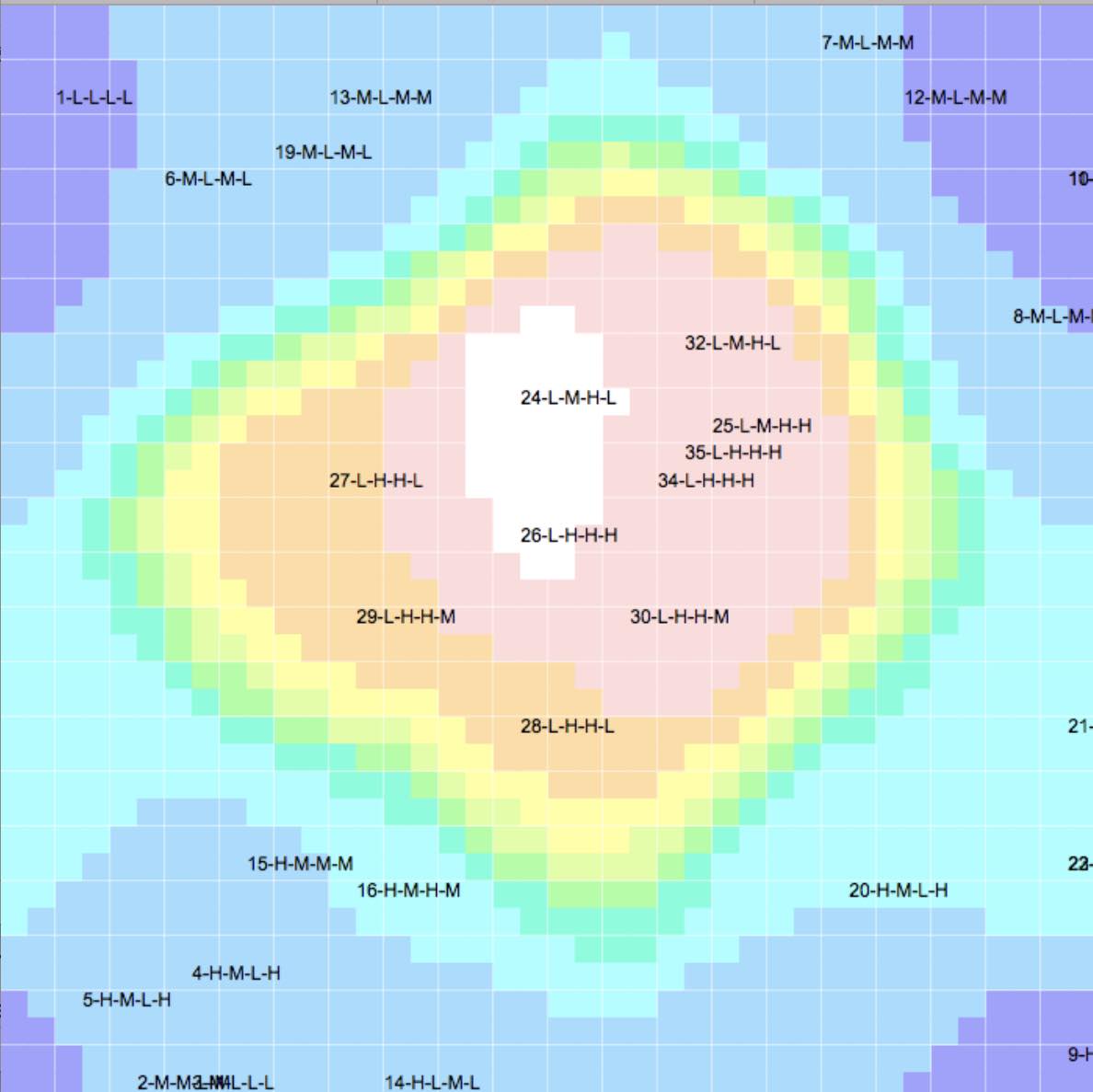
多次元ベクトルを2次元マッピングした結果は下図の様に表現される。
24-L-M-H-Lは図中のちょうど真ん中にある。
このL-M-H-Lのパターンが近いものは、近い位置に配置される。
4つが同じパターンではほぼ重なり、3つが同じものは近い位置に来る。
例えばRun-24の破断強度をMからHに変えた、L-H-H-Lの処方を検討しようとした時には、RUN-27,28を参考にすれば良いことがわかる。
RUN24とRUN-27,28ではパーオキサイドの種類が違う。
中々そうした系統の異なる実験はしないものなので、情報学のこうした提案は新鮮な提案になるはずだ。
これまでのMIの主流は、第1回で紹介したMultiscale Computational Hierarchyを基礎においている。
原子、分子、分子集合体、物質と、図中左下から右上に向かって研究が進行している。
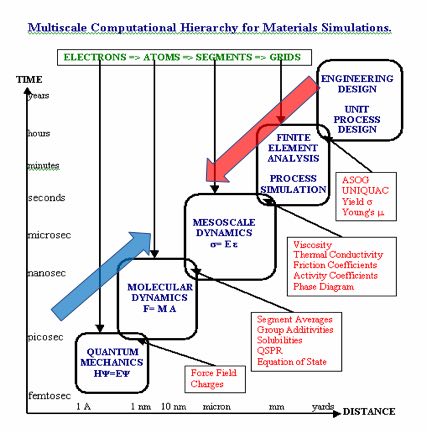
しかし、この方法でMaterial Integrationするには、生ゴムと、例えばカーボンブラックの相互作用を見積もり、架橋が時間とともにかかり粘度が変化する過程を解き明かさなくてはならない。
しかも、カーボンブラックの諸元の違いなどを知ることもなしに。
そこで、この方法で左下から右上に登っていこうとすると、材料の複合化は非常に難しい、乗り越えるのが大変な壁があることがわかる。
しかし方向を逆に考えて、すでにあるマクロの物性値を構造に落とし込んでいくと、比較的簡単に複合化を達成できることを今回示した。
いわゆる計算機化学というと、反応の様なミクロな、非常に短い時間の問題を解くには有利である。
化学工学は実時間、実サイズを扱う。
化学情報学は、そうした化合物の持つ情報を、全て受け入れてしまう懐の深い学問である。
コンピュータを使うので計算機化学の一部と思われがちだが、それは大間違いである。
雑感
筆者は授業の際に、毎年同じアンケートを行う。
年々文章は短くなり、語彙は減って行っている。
三行を超える長い文章の意味を捉える能力が低くなっている。
長い解説も同じであろうから、分割することにした。
SNSの時代、しょうがないことではあろうが、ここまで本を読まない大学(院)生は世界に稀であろう。
デジタル・ネイティブなどと言われている様であるが、全く逆だと思う。
学生はマテリアル・ゲノムやインダストリー5などという言葉すら知らない。
知らないものは検索もできないので、無いのと同じだ。
筆者のHPなども学生にとっては存在しないのと同じなのであろう。
それでも、今の時代、筆者の書いたものは自動的に翻訳され世界中の学生が読む。
自動翻訳させるなら、複雑な係り受けはしない。
難しい単語は使わない。文章は短めに。
あれ? 日本の大学生が読んで理解できる様に書けば自動翻訳させやすいのか。。。。
そんな状況で売り手市場とか言って浮かれている。
もう4−5年してAI-ロボットが本格的に実用化された時に“そんなの聞いていないよ”とならない様に祈るしかない。
ビッグデータと自然言語解釈、画像認識の技術は、いまは華やかであるが、化学や最先端素材開発と親和性が高いわけでは無い。
この分野にはビッグデータなどそもそも存在しないし、MOやMDでデータを水増しさせようにも、商品名しかわからない様な材料は計算のしようが無い。
しかし、現実問題としては今回紹介した様な方法で、研究を加速しているところは実在している。
情報化学+教育 > MAGICIAN 養成講座 > 講義資料 > 第3b回ポリマーの配合処方設計
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
