2021.9.20
情報化学+教育 > MAGICIAN 養成講座 > マイクロ波と3つのMI > その3、データ解析
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
その1と、その2で目的変数と説明変数のセットは手に入りました。
マテリアルズ・インフォマティクスの王道からいえば、後はビッグ・データをPLSやニューラルネットワーク法(NN法)、ディープ・ラーニング(DL)法で予測式を作れば良い事になります。
問題は、頑張ってもビッグデータと呼べるようなデータが集まらないという事です。
こんな材料は反応が加速(高い目的変数)した。
などというデータはどんどん増えていますが、他の反応と比較できない。
目的変数はあっても、説明変数が入手できない。
そこで、今回は、大学の授業で使っている、私の自作Webアプリ、YSBという解析ソフトを使う事にします。このアプリはYMBの一部となっています。使い方はこちらを参照してください。
ここで行いたいことの確認
マイクロ波を照射したら、どのくらい昇温するかを予測したい。
その昇温の大小に影響を与えるかどうかは不明だが、いくつかの説明変数がある。
そこで幾つかの説明変数を選択して
Y(昇温温度)= F (Xk, Xl, Xw・・)
と表す事ができる関数Fを求めたい。
つまり、変数選択と関数の決定を行いたい。
特に、YMBやRDKitを用いた場合は説明変数の数がとても多くなります。
マテリアルズ・インフォマティクスの王道からいえば、主成分回帰やPLSなどを使って、次元縮退を行うと教えます。
pirikaのページでも上記リンクで説明しているので、興味があればやってみるのも良いでしょう。
ここでは、最も簡単なYSBの変数選択重回帰法を使ってみましょう。
YSB-変数選択重回帰法
有機物の解析
今回集めた1分間照射時の到達温度のデータは26個ありました。YMBの吐き出した数値データは44あります。
次のようにX軸を到達温度として、Y軸にYMBで計算した数値でグラフを書きます。
こうした関係を1対1の関係ということで、単相関といいます。
例えばMW(分子量)との関係を見ると、ほとんど相関がない事がわかります。
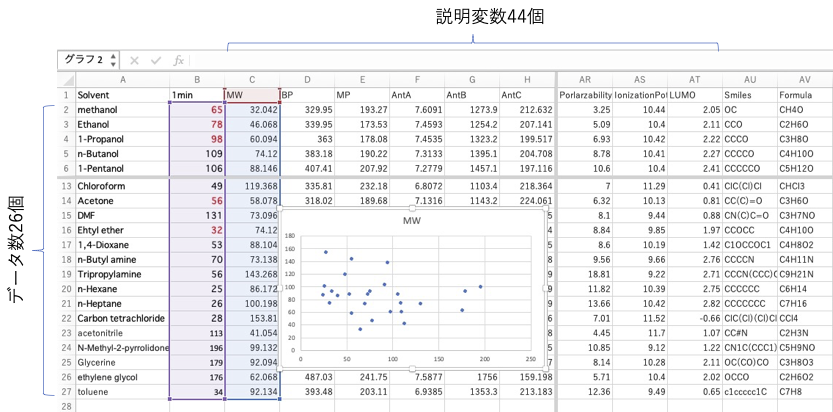
どの物性値との単相関が一番良いか?を調べるには、グラフを動かしていけばすぐわかるでしょう。
蒸気圧を計算するのに必要な、Antoine定数Bとの相関が一番高いです。
Antoineの蒸気圧式は次のようになります。
log (PmmHg) = Antoine A – Antoine B/(Antoine C+ T℃)
AntoineBが大きい化合物は、同じ温度T℃で蒸気圧が小さくなります。
そして、そのような化合物の到達温度は高くなる事を示しています。
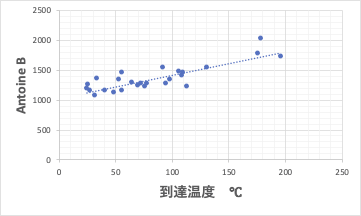
おそらく、マイクロ波をやっている先生の論文で、到達温度とAntoine定数Bを相関付けたものはないと思います。
下図に示す誘電率との相関から見ても遜色は無いと言えるでしょう。
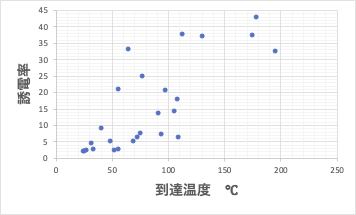
この辺りが、データ駆動型サイエンスの気持ちの悪いところでしょう。
理由は後でゆっくり(頭の良い人が)考えれば良い。
単相関の次に行ってしまいましょう。
重相関
これまで、10年以上大学院の学生に講義していて、学生がエクセルの分析ツールをインストールしてあったことは、1人きりでした。ということは、化学系の学生は大学院の1年生でも、重回帰計算はやったことはない事になります。
例えば「暑さ指数」というのはご存知でしょうか?
熱中症になりやすさは、気温だけでなく、湿度とも関係があります。
正式には「湿球黒球温度」と言い、英名のWet Bulb Globe Temperatureの頭文字から、WBGTと呼ばれます。
乾球温度(気温)、湿球温度(気温と湿度)、黒球温度(輻射熱などに関係する温度で、直径15cmもしくは7.5cmの黒球中の温度)の3種類の温度を計測します。
- 屋外で日射のある場合:
WBGT(℃)= 0.7×湿球温度+ 0.2×黒球温度 + 0.1×乾球温度 - 室内や屋外で日射のない場合:
WBGT(℃)= 0.7×湿球温度+ 0.3×黒球温度
これと同じように、到達温度が、複数の説明変数を使った関数で表す事ができるとして、どの説明変数を使って、その時の係数はいくつの時、目的変数を一番よく再現できるかを考えます。
「単相関で高い相関があったものだけを組みあわせれば良い」わけではありません。割れ鍋にとじ蓋で補完しあっていてもよいのです。
先ほどの単相関の場合は,44種類を考えれば良かったです。
44変数の中から2つ変数を選ぶやり方は、44C2(コンビネーションの計算:44*43/(2*1))で946通りあります。3種類選ぶのは、44*43*42/(3*2*1)とだんだん場合の数が増えます。
詳しい説明は省きますが、YSBでは遺伝的アルゴリズム法(GA法)を使い、限られた時間の中で、最も良い変数の組み合わせを提案します。(場合によると選ばれる変数が毎回異なります。)
最も良いというのは、相関係数が一番高いものを言います。
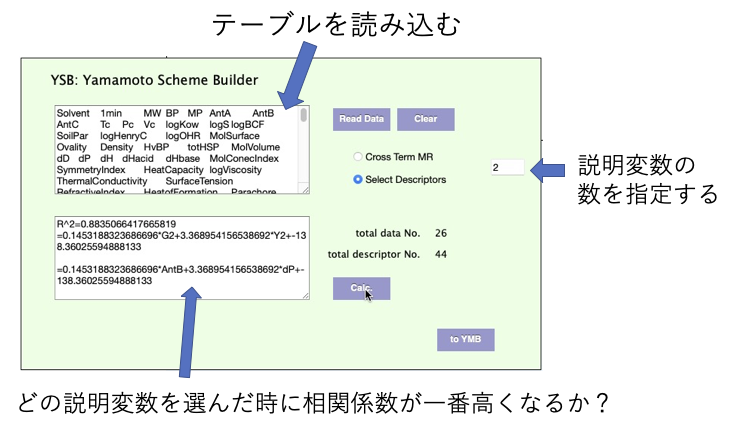
説明変数を2つ使うのであれば
R2 =0.8835
0.1453*AntB+3.3690*dP-138.3602
説明変数を3つ使うのであれば
R2 =0.9200
0.2800*AntB-18.818*Pc+-48.6184*MolConecIndex+-83.9854
説明変数を4つ使うのであれば
R2 =0.9343
0.3029*AntB+-5.7076*totHSP+-43.6553*MolConecIndex+3.111*pKa+-125.3656
説明変数を5つ使うのであれば
R2 =0.9381
0.2924*AntB+-3.2778*totHSP+-33.925*MolConecIndex+-135.1313*MinMinusCharge+0.0978*StdGibbsEoFormation+-169.66876176457572
説明変数を6つ使うのであれば
R2 =0.9408
=0.2859*AntB+-6.6523*totHSP+2.5842*dP+-36.4622*MolConecIndex+2.6807*pKa+2.7884*LUMO+-120.0832
となりますが、特に変数が多い場合には、やる度に選ばれるものは変わります。
また、決定係数(相関係数の2乗)も微妙に変わってきます。
この辺りは、サラブレッドの馬を、進化論的に改良していくような、遺伝的アルゴリズム(GA)を用いているので、難しいところでもあり、面白いところでもあります。
説明変数を何個にしたら良いのかは、最初は迷うところでしょう。
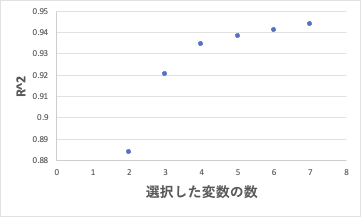
通常は選択肢変数の数が多くなると決定係数も高くなります。
ところが、あるところをすぎると、上昇率が寝てきます。
私は、こうした時は、4-5ぐらいのものを選びます。
もしくは、乳酸やコハク酸、無機物では黒鉛のように、値が大きくなる事が明らかなものを予測してみながら判断していきます。
また、何度も選択を繰り返し、全く選ばれなかった説明変数を消していったりします。
例えば、Antoine定数、臨界定数、HSPなどグループで意味のあるパラメータで式を作成するなどを繰り返します。
マテリアルズ・インフォマティクスでは、ランダム・フォレストのようにランダムにとったグループでの合議制で推定することが行われますが、意味のあるパラメータの組みはランダムでは見つからないので、化学的な常識を人間が補う必要があります。これは、化学者ならではの腕の見せ所になります。
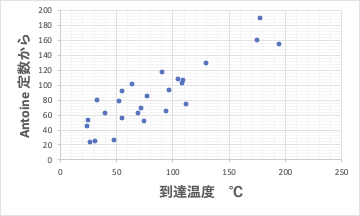
Antoine 定数だけから予測式を作成
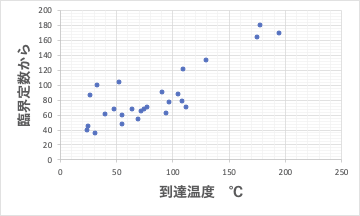
臨界定数(Tc, Pc, Vc)だけから予測式を作成
ハンセン溶解度パラメータ(dD,dP,dH)だけから予測式を作成
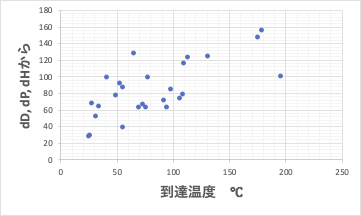
このようにたくさんの系列の異なる予測式を作成し、どんな化合物が合わないのか特定して行きます。
そして、なぜ合わないのか考えます。例えば常に大きな分子が外れるようであったら、分子体積を説明変数に加えます。この部分が化学者として一番大事なところです。
さらに系列を変えて、トポロジカル・インデックスなどが多い、RDKitのデータから変数選択して予測式を作ってみましょう。変数4で式を作るとChi0n, Chi3v,NumAliphaticCarbocycles,TPSAの4変数が選ばれました。
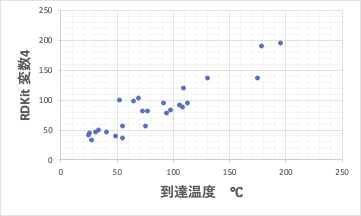
ここで得られた重要なトポロジカル・インデックスをYMBの結果に混ぜていくのも良い考えです。
無機物の解析
無機物に関しても解析に関しては同じです。
元素単体の系に関しては、18識別子から、Electronegativity、電子親和力、Atomic Mass、SP@BPが選択され、その時の回帰結果をグラフ化すると次のようになります。
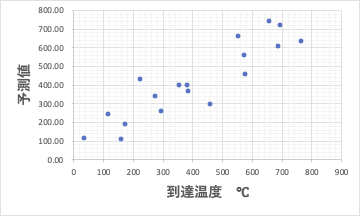
これが出来上がると、Rhに5分マイクロ波を照射したら何度になるか?という問いに関して600℃超であると答える事ができるようになります。
式の改訂
解析を行う部分は、このぐらい簡単に行える必要があります。
それは、式を頻繁に改訂する必要があるからです。
計算結果を受けて実験を行ってみた。計算と合わなかった、その結果を入れて式を組み直して、次の実験につなげる。それを高速に繰り返す事が開発の効率化に繋がります。
ハイスループットの実験と組み合わせると、さらに有効です。
テーブルに穴がある場合の解析
金属酸化物の識別子のテーブルは、データが4つ欠損しています。
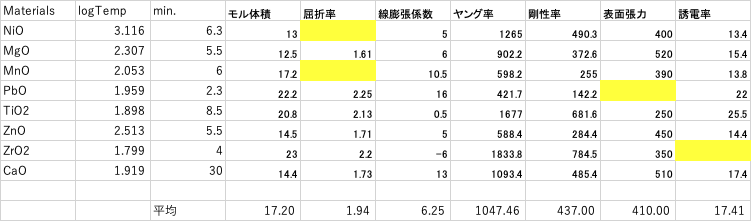
これを解析するためには、欠損データのある4酸化物を消去するか、屈折率、表面張力、誘電率の列を消去しなければなりません。元々少ないデータなのにそれを消去するのも嫌ですし、変数選択した時に大事な列である可能性もあります。そのような時は、とりあえず平均値を入れてモデル式を作ってみましょう。
汚いデータを削ぎ落とすのが大変です。
変数3の変数選択重回帰式
照射時間、モル体積、屈折率の3変数が選択されました。
屈折率に関しては、NiOとMnOに欠損値があって、平均値が入っています。
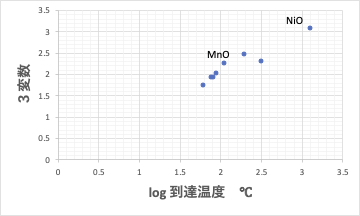
このグラフを見る限り、NiOとMnOが大きく乖離しているとは言えないので、平均値で大きくは間違っていないようです。
念の為、変数4の変数選択重回帰式を作ると、さらに線膨張係数が選択されました。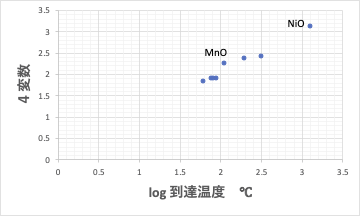
このグラフで見ても取り敢えずこの推算式でスタートできるのでは無いかと思います。
そして可能であれば、この酸化物を含む複合酸化物の屈折率を収集し値を確定すれば良い事になります。
情報化学+教育 > MAGICIAN 養成講座 > マイクロ波と3つのMI > その3、データ解析
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
