2021.9.30
情報化学+教育 > MAGICIAN 養成講座 > マイクロ波と3つのMI > その6、さらに先へ 比誘電損失の周波数、温度依存性
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
これまでの検討では、Big Dataはないと言う前提で色々解析を行ってきました。それでもやれる事は色々あることはお分かりいただけたと思います。そういう研究も好きなのですが、それ以外にもMAGICIANには色々な事ができます。
今回の、マイクロ波の解析で、有機物に1分間マイクロ波を当てた時の到達温度は、蒸気圧を計算するAntoine定数Bと相関が高いという話をしました。
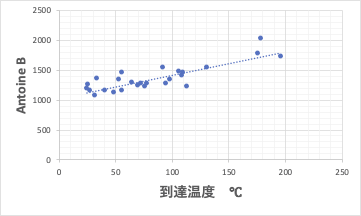
データ駆動型の研究では、なぜその識別子が選ばれたかはあまり問題にしませんが、もう少し詳しく考えてみましょう。
化合物にとっての温度の意味
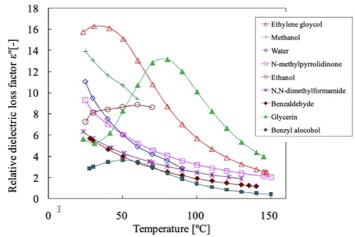
例えば「マイクロ波の化学」三共出版に、様々な溶媒の25℃における、比誘電損失の周波数依存性のグラフがあります。
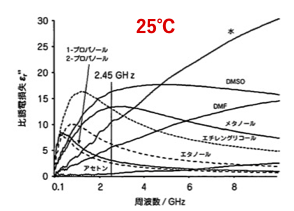
我々は、ついつい、地球基準の温度で25℃を基準にこのようなグラフを描きます。
しかし、化合物にとっては25℃は全く基準にはなりません。
同じ25℃でも南極の冬のように感じて身動きできない状態であったり、沸騰寸前であるかもしれません。
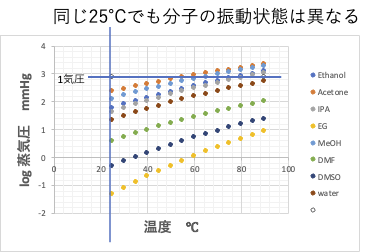
そこで分子の基準温度は臨界点か3重点にしないと比較できません。
詳しいことはこちらで説明しています。pirikaの沸騰の化学
簡単に説明すると、化合物に熱をかけると、温度、圧力には次のような関係になります。
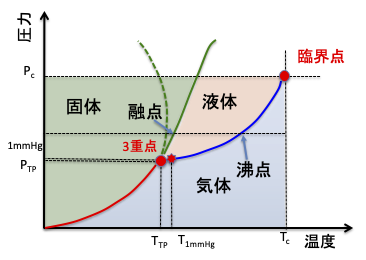
ここに、基準点として臨界点と3重点があります。
3重点は一般には得られないので、多くの場合、臨界点を基準にした、対応状態原理法による物性推算式が開発されています。
簡単に言ってしまえば、化合物ごとに臨界点は異なるけど、そのPVT関係の臨界軌跡は同じになります。
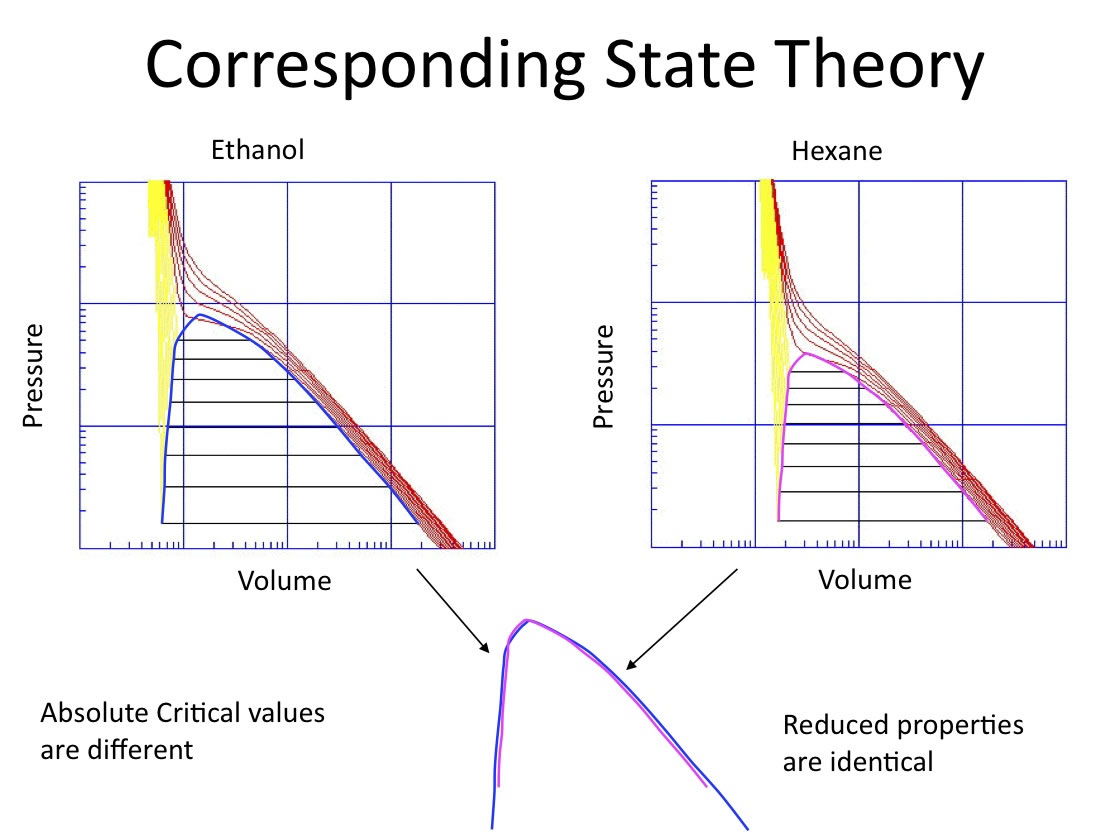
そこで、任意の温度、圧力の時の物性値は臨界点からの距離で決まることになります。
ですから、各化合物の25℃と言うのは、(25+273.15)/臨界温度[K]で変換すると分子にとっては比べられる指標になります。
しかし、一般には、25℃は臨界温度(液体からガス)からは非常に遠いところになります。3重点(固体、液体、気体が平衡)の方が25℃には近いのです。
そこで、圧力が1mmHgになる点を考えます。その時の温度はT1mmHgになります。
T1mmHgは化合物ごとに異なりますが、その温度では、分子間力に打ち勝って蒸気相へ飛び出す分子は1mmHgなので共通になります。
そこで、山本は1mmHg, T1mmHgを分子の基準に置いています。
蒸気圧を計算するAntoine定数A, B, Cが求まると、蒸気圧は次式で計算できます。
log Pressure mmHg=log(1)=0=AntoineA – Antoine B/(Antoine C+ Temperature℃)
AntoineA = Antoine B/(Antoine C+ Temperature℃)なので
T1mmHg=(Antoine B/Antoine A) – AntoineCが求まります。
この考えに基づくと、分子の運動エネルギー(周りの分子の束縛を振り切って気相に飛び出す)を同じにする換算温度はAntoine B/(Antoine C+ Temperature℃)で定義されます。
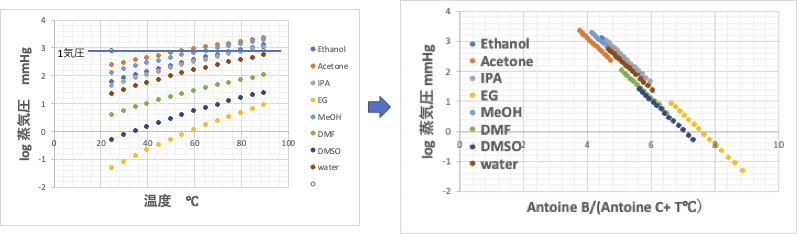
水素結合性の化合物とそれ以外では少し異なりますが、同じ換算温度では同じ分子の運動状態であるとします。
ニューラルネットワーク用学習データ
エタノールとエチレングリコールに関しては周波数と温度を変えたデータがあります。
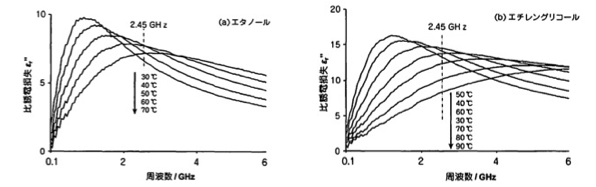
これをデジタイザーで読み込みます。
比誘電損失の周波数依存性の最初のグラフは25℃のデータですが、換算温度でみると、4.66-8.3の間のデータになります。
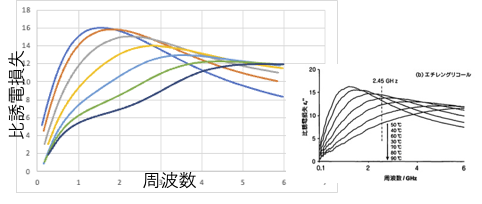
エタノールのデータは温度にして30-70℃ですが換算温度としては4.51-5.27になります。
エチレングリコールは温度にしては30-90℃ですが、換算温度としては6.19-8.09になります。
JFCC 体材料における誘電率の温度特性評価には水の誘電損失のデータが記載されています。
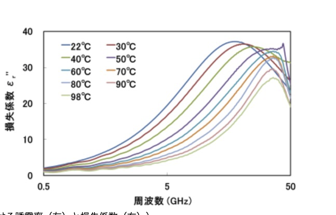
フロー処理型マイクロ波化学反応装置の開発とマイクロ波効果の検証 博士論文には、温度依存性のデータが載っています。
そしてニューラルネットワーク法で学習用のデータセットを次のように作成します。
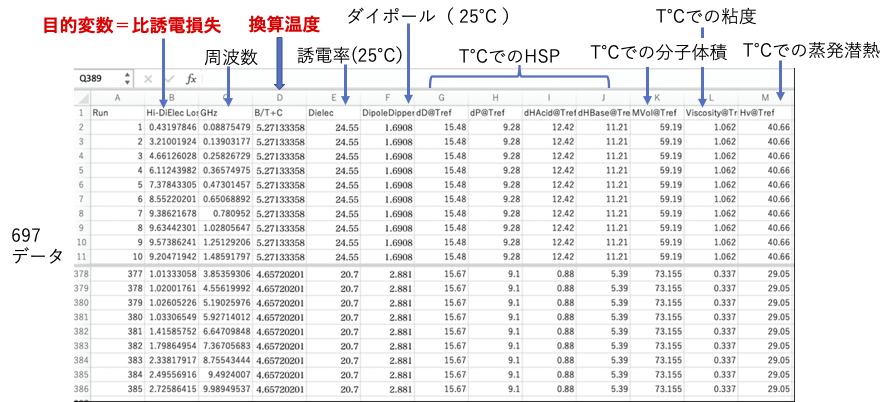
目的変数は比誘電損失です。周波数と温度に依存するはずですが、ここでは統一的に扱えるように換算温度にして学習させます。
5つのチャートからデジタイズしているのでデータ数は697データと比較的多くのデータになっています。
ニューラルネットワーク学習
これを自作のニューラルネットワークシミュレータに学習させます。
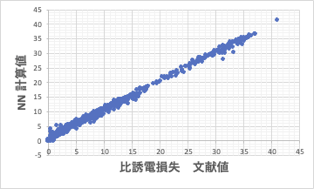
良好に学習できているようなので、結果を元の5つのチャートに分割して検討します。
まず25℃一定のデータだけ取り出すと次のようになりました。
それなりに再現できている事がわかります。
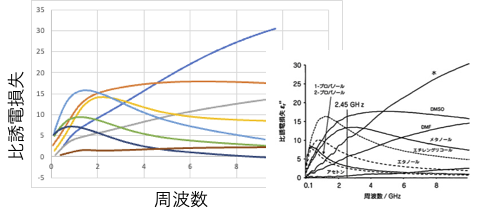
エタノールの温度と周波数依存性は次のようになります。
山のシャープさが少し足りないでしょうか。
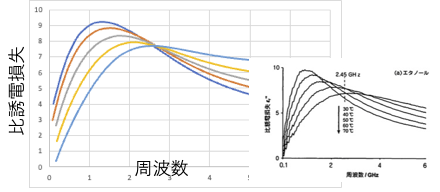
エチレングリコールは特に温度が高いところで少し再現性が悪いです。
水の再現性
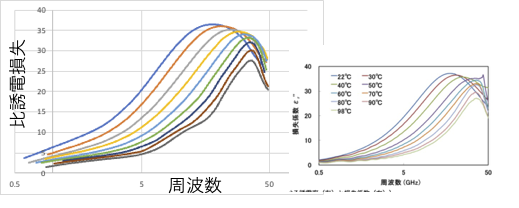
温度効果の再現性
こうした結果を見て、私がイメージする比誘電損失は、ゼンマイのようなものかなと。
温度が高くなると、ゼンマイが弱くなってしまうけど、その弱くなり方は換算温度に依存していて、℃では比べられないといったイメージです。
このように、MIは色々な考えるネタを与えてくれます。
本来はこうして作ったニューラルネットワーク・システムもWebアプリとして自由に使ってもらう情報発信も大事なのでしょう。
学習に使ったデータから、あるものにマイクロ波を当て温度が上がったら、誘電損失のピーク周波数を予測し、常にピーク周波数で加熱するなどもできるようになるかもしれません。
でも、私が興味のあるのは、どうしても、「何故?」に対してどう「理解」できるかです。
上に凸の山の高さと位置
温度一定で周波数を変えたときに、メタノールやエチレングリコールで上に凸の山ができます。 その位置や高さは化合物によって異なります。

それに対して、これはジュール加熱と誘電加熱が混じった効果だと教科書は説明します。
そして、それはεs, ε∞, ω、τ、σで計算できるとあります。
では、次のような温度が変わることによって現れる山はどのように理解できるのでしょうか?

εs, ε∞, ω、τ、σの温度依存のデータが手に入るのでしょうか?
無いものねだりしていてもしょうがないので、「化学者の常識」で考えます。
例えば、温度が上がる時に大きくなる物性値にはどんなものがあるでしょう?
逆に、温度が上がると小さくなる物性値にはどんなものがあるでしょう?
蒸気圧は温度が高くなれば大きくなることは先に触れました。
例えば温度が高くなれば、粘度は低くなります。
ここで大事なのは、この常識はどんな化合物に対しても通用しますが、蒸気圧も、粘度も化合物によって異なると言うことです。
蒸気圧に関しては、分子換算温度を使うことによって分子に寄らない取り扱いが可能になることは先に示しました。
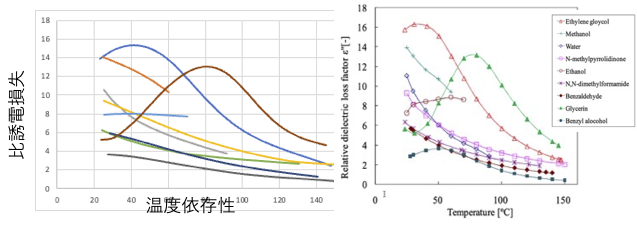
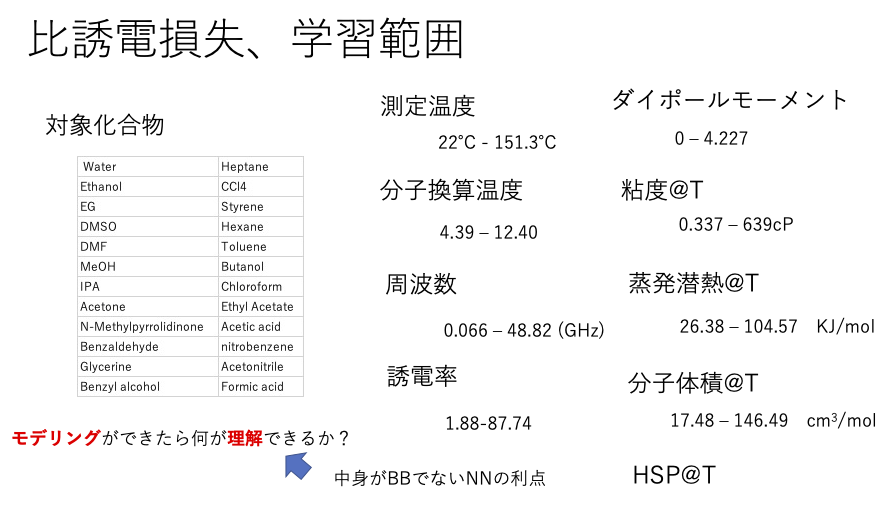
同じように粘土のデータを処理して見ましょう。
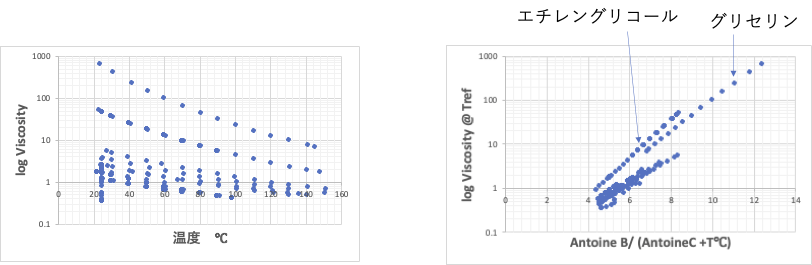
粘度は温度に対して分子ごとに特有の曲線を描きます。
そして、温度を分子換算温度に変えると、3次元水素結合を作るグリセリン、エチレングリコール以外の化合物は、同じ直線に乗ります。
電場をかけた時に、分子が周りの分子の束縛に逆らって動く。
蒸発というのは、熱をかけた時に分子が周りの分子の束縛に逆らって運動する。
粘度というのは、分子が動こうとしたときの抵抗です。
さらに、
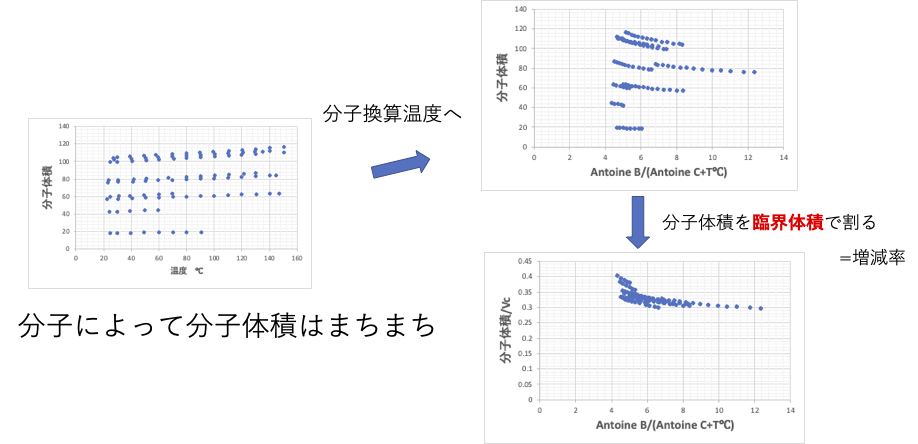
分子体積も温度上昇によって大きくなる分子固有の物性です。
分子換算温度をとり、さらに臨界体積で割った、増減率で見れば分子により違いなどは無くなります。
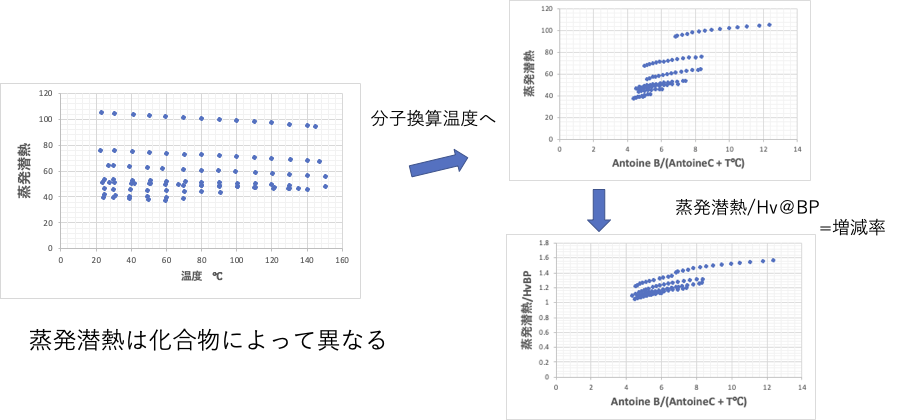
蒸発潜熱は温度上昇によって小さくなる分子固有の物性です。
分子換算温度をとり、さらに沸点における蒸発潜熱で割った、増減率で見れば分子により違いなどは無くなります。
こうしてくると、私がニューラルネットワークの入力データにこうしたものを選んだ理由がお分かり頂けると思います。
分子の違いを吸収するのが大事なのです。
私はマイクロ波に関しては、全くの素人です。
今回書いたようなMI的な取り扱いが正しいかどうか、実験をできる立場でもなく、デジタイザーで起こしたデータで論文を書くなどあり得ません。
でも、MIによって作ったAI-アシストのおかげで、とても豊かな考え方ができていると思っています。
他の研究者に対して、AI-アシストを自分で育てられるという優勢性があります。
純粋AIとの戦いは、AIには化学の常識は無いので、あまり気にしていません。
欧米、中国などのAI-アシスト系の研究者とはガチでぶつかります。
でも、そうやってガチでぶつかって切磋琢磨していくのが大事だと思っています。
今回のデジタイズしたデータを置いておきましょう。
我こそは、と思うMI系研究者は、自分で識別子を考えて、pirikaを超えるAI-アシストを作って頂きたいと思います。
評論だけしたい人は、どうぞ、他所でご活躍ください。
幸い、機械翻訳は非常に進歩しました。
日本語以外でも、いくらでも深い議論を行える相手に巡り会える、ありがたい時代です。
DXというのは
IT技術を使いこなせるように、「自分を変えていく」ではありません。
IT技術を使い、社会や環境をどう豊かに「変えていくか」の問題です。
豊かさの定義が問われる時代になったということです。
情報化学+教育 > MAGICIAN 養成講座 > マイクロ波と3つのMI > その6、さらに先へ 比誘電損失の周波数、温度依存性
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
