2011.5.29
その他の化学トップページ> YNU-シミュレータ
HTNL+JavaScriptの手習で、昔作った(1990)Cのプログラムをブラウザー上で動くように改造した。現在では意味ないが、思い出の品として。
iPadで分子の半経験的分子軌道計算(CNDO/2):
自分は、分子軌道法を使って遷移状態を求め、反応速度定数を算出するという事をやっていた時期がある。その際には半経験的分子軌道法では全然精度がでないで駄目で、ガウシアンというAb initioプログラムを使って、何週間もかけて計算を行っていた。これは特殊な例で、化学工学の学生がガウシアンの使い方を知る必要は殆ど無いと思う。 MOPACという半経験的分子軌道法のパッケージ・ソフトが使えれば事足りるだろうが、MOPACにしても使いこなそうとしたら5コマ(10時間)の授業時間全部を使わなくては無理で、化学工学特有の問題にまで踏み込むには無理がある。そこで、分子軌道計算から出てくる計算可能量のうち、化学工学特有の問題に適用できる最低限の物性値をここでは取り扱っていこう。
まず、最初に簡単に分子軌道法について説明しよう。原子の周りには電子が回っている。太陽の周りに惑星が回っているのをイメージして欲しい。一番内側に水星、次に金星、地球、火星とだんだん距離が離れたところを回っている。原子も同じで原子核の近いところを回っている電子と、離れた所を回っている電子がいる。惑星との違いは、惑星は円を描いて(平面を)回っているが、電子は同じ距離ではあるが球の表面を回っている。近いところを回っている電子は球の表面を回っているが、外側になるに連れ、彗星のように偏った軌道を取るようになる。そうした軌道のうち、球の軌道をとるものをS軌道、その上はP軌道、d軌道、f軌道とどんどん複雑なまわり方をする。各軌道には電子が2個まで入る。原子が組み合わさって分子になると、この原子軌道が混じり合って分子軌道を作る。それでも基本的考え方は同じで、分子軌道の一番エネルギーの低い軌道からから順番に電子が2個はいる。元素の周期律表はその電子の入り方で整理されている。そして原子が持っている電子の総和分だけ低い方から軌道が埋まっていき、一番高いエネルギーの軌道をHOMOと呼ぶ。その上には電子が入っていない軌道がある。そのうち一番低いエネルギーの軌道をLUMOと呼ぶ。電子が紫外光などのエネルギーを受けて励起すると、HOMOからLUMOへ飛び移り、光や熱を放出してまたHOMOの軌道に戻る。原子と原子がくっついて分子を作るときには、こうした電子が接着剤のように原子と原子の間にいる確率が高くなる。それを結合と呼んでいる。その結合の種類にはシグマ(σ)結合とパイ(π)結合がある。
それでは、YNU-シミュレータを使って実際にやってみよう。まず最初に最初の授業で伝えるパスコードを入力する。(パスコードがないと使える原子はH, C, N, Oだけになる。)
まず、エチレンを組み立ててみよう。準備ができたらCNDO/2の計算画面に行く。
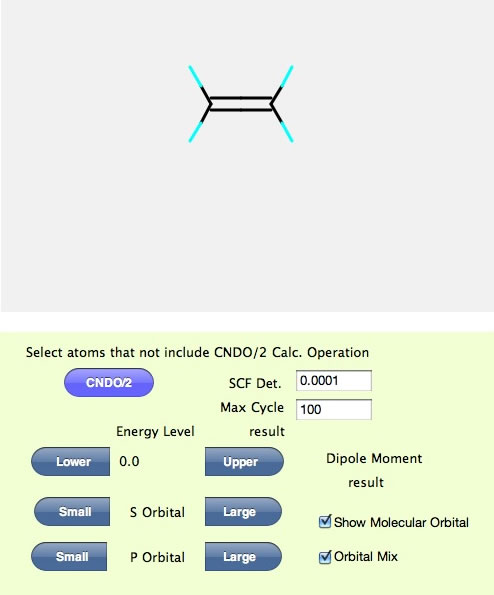
そしてCNDO/2のボタンを押す。
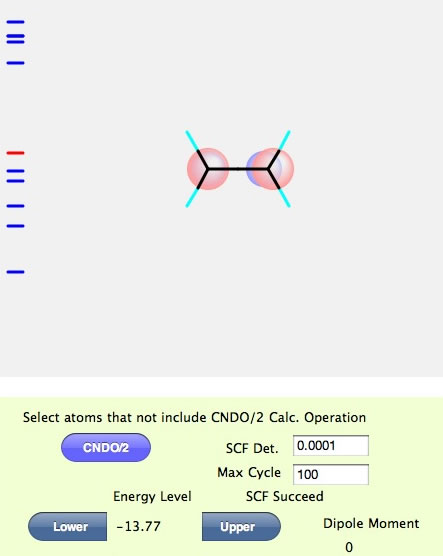
このような画面になったら計算は成功だ。SCFというのは、Self-Consistent Fieldの略で自己無撞着場と訳されているが、矛盾なく分子軌道が求まりましたという意味ぐらいに覚えておいて欲しい。左側のところにバーコード見たいのが表示されている。これは分子軌道のエネルギーレベルを表している。赤い線は今表示されている分子軌道のエネルギーレベルだ。最初に計算したての時には、HOMOになるようにしてある。従ってエチレン分子のHOMOのエネルギーは-13.77であることが判る。分子を回転させてみよう。
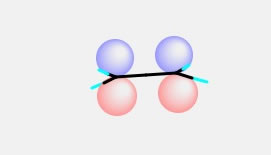
エチレン原子は平面原子だが、その平面に垂直方向へ4つの球が見えるだろう。これがエチレンのP軌道だ。最近のちゃんとしたソフトウエアーはContourという等高線図で軌道を表すのが主流であるが、自分は昔ながらのChrmDrawなどで利用したこうした表示の方が好きだ。(プログラムが容易であるというのもある)
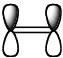
実はP軌道は方向性を持っているので、Px, Py, Pzの値を持っているのだが、この簡略化した表示システムでは、この方向をベクトルとして捉えて、そのベクトルの方向に球を描くという方法を取っている。(その方が分子を回転させたときに便利なので。)
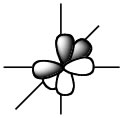
それでは、次にLUMOを見てみよう。
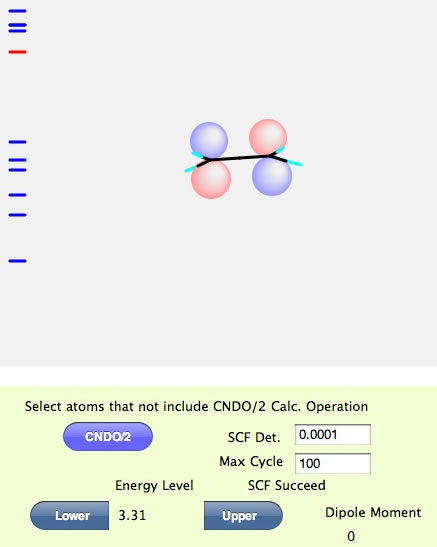
EnergyLevelの下にあるUpperボタンを押すと、LUMOのエネルギーが3.31なことが判る。そして分子軌道は赤と青の球が左右でひっくり返った形になる。このような場合に真中に節があるという言い方をする。色の違いは、同じ色同士は混じり合って結合を作ると覚えておいて欲しい。そこでエチレンのHOMOの場合にはP軌道同士が混じり合ってπ結合を作るという言い方をし、LUMOの場合には反結合性のπ軌道という言い方をする。エチレンが重合するときには、ラジカルがHOMOのP軌道をアタックして結合を作り、もうひとつの炭素がラジカルになって反応が進む。
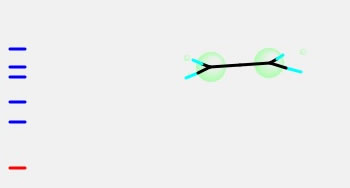
さらに下の方の軌道を見ていくと、同じ位相のS軌道があることがわかる。これらは内殻電子と呼ばれ反応には関与しない。。
下の方の軌道に行くと、球がいろいろな原子の上に分散して小さな球しか見えなくなることがある。その時には、OrbitalのLage Smallボタンを押して見かけだけ変えることができる。
アセチレンを組んで計算すると、次のようになる。
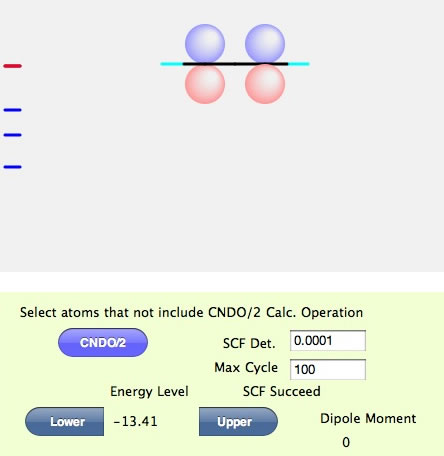
エチレンと同じように見えるが、Lowerボタンを押してみて欲しい。
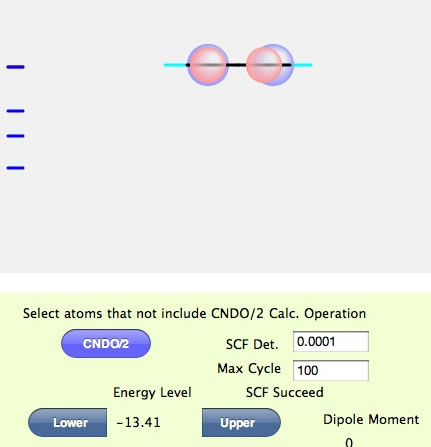
エネルギーレベルが全く同じで、パイ結合が画面に垂直に出来ていることが判る。これを軌道の縮退と呼ぶ。つまり、画面の上下方向のパイ結合と垂直方向のパイ結合は等価となる。この2つのパイ結合で3重結合を作っている。
例えば塩化ビニリデンを組んでみよう(パスコードを入れないと塩素は選択できない)。
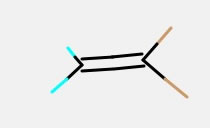
これをCNDO/2で計算すると下のようになる。
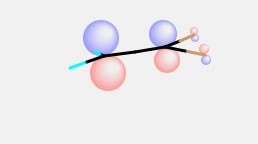
塩素がついた側のパイ軌道が小さくなることが判るだろう。多くのラジカル重合性のモノマーは、ヘッド(頭:置換基がいっぱいついた方)とテイル(尾:置換基が付いていない方)で、ラジカルのアッタクはテイルに起こる事が判る。(電荷もどうなるか調べてみよう。)もし、SCF Failと表示されたら、SCF Det.の値を思い切って大きくしてみよう。(計算結果は信用できないが、軌道を見る程度には役立つ。)
メタノールを組むときに、3次元構造に慣れた学生は、SP3(手が4本のピラミッド型)から、水素を2つ消去して構造を作る。
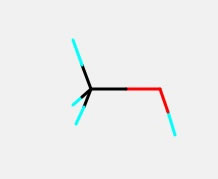
酸素は手が2本なので炭素-酸素-水素は直線でもいいように思えるかもしれない。
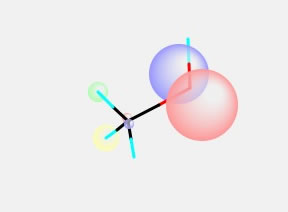
これをCNDO/2で計算すると、HOMOでは大きなπ軌道が酸素の上にあることがわかる。そのひとつ下の軌道をLowerボタンを押して見ると、
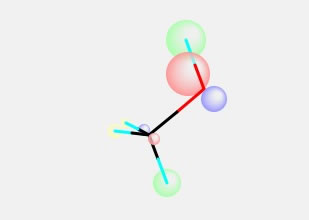
となる。青の球と赤の球のサイズが違って見える。(画面効果を上げるために、S軌道を大きくしている。)この場合は、Orbital Mixにチェックがかかっているのを確認して欲しい。このOrbital Mixは、ある原子上にS軌道とP軌道がある場合、符号をみながら、SとPの球のサイズを変えて表示する機能だ。この2つの軌道を合わせると、有機化学で下のように書く軌道が得られた事がわかる。
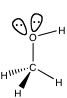
ローンペア(孤立電子対)とは、1つの軌道に電子が2つ入り,共有結合に関与しない電子対のことだ。酸素はこれが2組あるため、直線では無く4面体構造を構造をとる。(それを知らなくても、直線分子を作り分子構造の最適化を行えば正しい構造が得られる。)
最後にブタジエンの構造を作ってみよう。これは、Part Moveを使って、ねじれ角を回すと簡単に作れる。
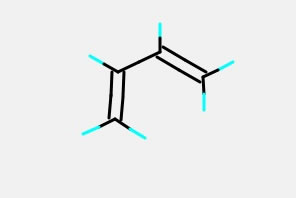
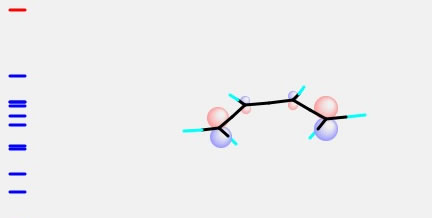
それのCNDO/2計算を行うと、下のようなHOMOが得られる。
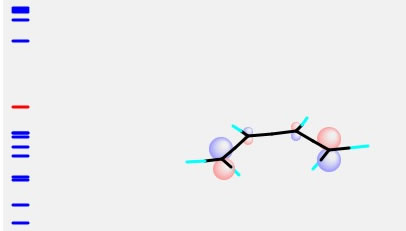
これはエチレンのLUMOと色が合わせられることが判るだろう。
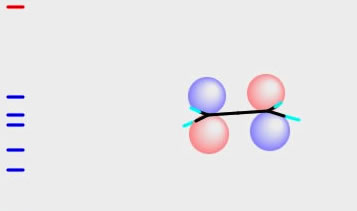
ブタジエンのLUMOは

エチレンのHOMOと色が合わせることができる。
これがノーベル賞をとったフロンティア電子理論(辺境、つまりHOMOやLUMO)だ。こうした結果から、ブタジエンとエチレンは反応して環状化合物ができる。エチレンのHOMOとエチレンのLUMOは色が合わない。だから4員環は生成しない。
CNDO/2でもこのくらいの事はできてしまうので、化学工学には十分だろう。こんな計算がiPadでできてしまうのだから驚きだ。
ここまでくると、3次元構造から得られる計算可能量が皆手に入った事になる。分子の2次元構造は3次元構造が得られていれば簡単に変換できる。そうした分子の2次元構造だけからも様々な物性が得られる。分子を原子団に分割して、その種類と数から物性を推算する原子団寄与法というのがある。次はその説明をしよう。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
