2024.9.10
pirika.comで化学 > 化学全般 > 高分子化学 >
B3LYP計算によるシーケンス解析
モノマーはどんなシーケンス(並び順で)でポリマーの中に入るのだろうか?
それを知るためには、実験でモノマーの反応性比を求めるのが実際のところ早道かもしれない。モノマーの比率を変化させ、4-5点重合を行い(濃度が変わらない程度の重合初期で打ち切る)、ポリマー中のモノマーの量をNMRなどで測定して、反応性比を得る。
多くの実験結果がPolymer Handbookに記載されている。
溶媒、開始剤、重合方法、重合温度によって反応性比は異なる。
そこで、ある程度大雑把で良いから、反応性比を予測したいというニーズはある。
B3LYP/6-31G**でラジカルとモノマー(30種)の遷移状態を432系計算し、活性化エネルギーと頻度因子を求めた。まー、当時暇人だった。
その活性化エネルギーと頻度因子を推算するニューラルネットワークを構築した。インプットはMOPACで計算したモノマーとラジカルの情報だ。
そのニューラルネットワークが反応速度定数を、どんなモノマーであっても(MOPACで計算さえすれば)予測してくれるなら、非常に手軽にポリマー・シーケンスを予測してくれることになる。
ここでの計算は2005にJavaで作ったものをJavaScriptに変えただけで新しいものではない。
以降、古い記述。
ただし、分子軌道計算がどの程度、実際の反応を再現できるか?はよく吟味するする必要がある。
例えばいろいろなラジカルがモノマーのHeadに付加するか、Tailに付加するかの実験値に対して、計算のレベルを変えて評価したテーブルがある。
この反応は気相反応なので、比較的計算値とは合いやすいはずであるが、ラジカルが混み合うにつれ実験値とは大きく乖離する。
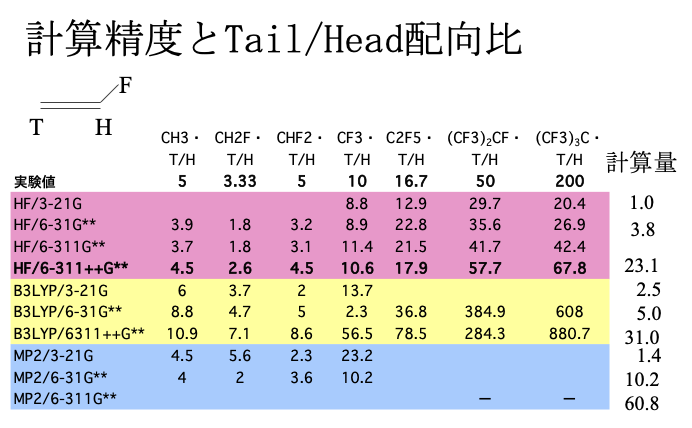
つまり、ニューラルネットワークが精度良く推算すると言っても、ラジカルの周辺が混み合っている場合には、結果は割り引いて考えなくてはならない。
元々、自分のような実験屋は、計算自体をそんなには信じていない。どのみち、下駄を履かせて考えるなら、無駄に計算時間の長い基底関数を使うくらいなら、MOPAC程度の計算を行なってニューラルネットワークで下駄を履かせる方が性に合っている。
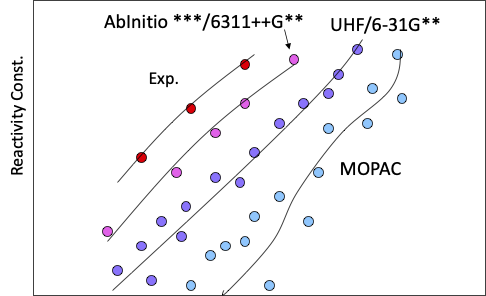
とは言いながら、次のテーブルの黄色く塗られた部分と、Oの部分は計算した。一つ求まったら、遷移状態の大事な部分はそのまま、置換基を変えて計算するだけなので簡単ではあったが。取り敢えず仕事している感満載になる。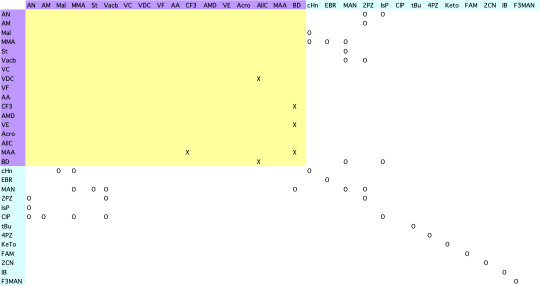
今では化石のようなデータなので、良い子は参考にしてはいけない。
pirikaの現状では、Qe値法を使うことにしている。
pirika.comで化学 > 化学全般 > 高分子化学 >
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
