2024.9.10
pirika.comで化学 > 化学全般 > 高分子化学 >
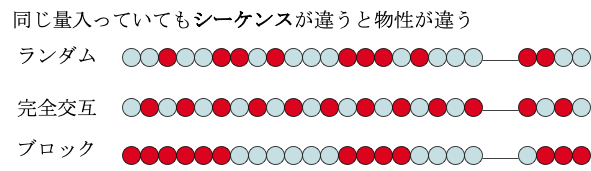
ポリマー中のモノマーのシーケンス（並び方）
ポリマーの研究の難しいところは、非常に多くのモノマーが存在し、その組み合わせが自由なことだ。そしてモノマーの種類が異なった場合にできるポリマーも異なることだ。
最近の風潮としては精密重合で欲しい構造のポリマーを作るということもある。しかし工業的スケールで安価なポリマーを作るのであれば、シーケンス解析を利用したポリマー製造はまだまだ大事な分野だ。
このシーケンスを知るためには、反応速度定数(比)を知る必要がある。
反応速度定数(比)はPolymer Handobookなどに記載されている。しかし、自分がほしいモノマーの組の反応性比が得られるとは限らない。
また、モノマーごとに決定されているAlfrey-PriceのQe値を用いて反応性比を計算することも可能だ。しかし、これも簡単に手に入るものではない。
分子軌道計算を用いた反応速度定数の算出
ラジカル末端とモノマーの遷移状態を算出する。最初はHF法で計算したが、共役系のモノマー、スチレンで合わなくなるので、密度汎関数法(B3LYP)で遷移状態を求めた。
モノマーペアで４つの遷移状態を求めなくてはならない。
A・＋ B → AB・
A・ + A → AA・
B・ + B → BB・
B・ + A → BB・
いきなり高精度の計算をするのは大変なので、まずは半経験的分子軌道法MOPACで遷移状態を求めた。その構造をフォーマット変換してB3LYP計算した。
MOPACの遷移状態での虚振動はこちらで見ることができる。
新しいモノマーを高精度に計算し続ける手間を避けるために、情報化学を用いた推算式を構築しておく。
ニューラルネットワーク法を用いた活性化エネルギーと頻度因子の推算
重合シミュレーション
ニューラルネットワーク法を用いた(B3LYP計算相当の)シーケンス解析
Alfrey-Price Qe値を用いた反応性比の算出
r1=Q1/Q2 ・e -e1(e1-e2)
r2=Q2/Q1 ・e -e2(e2-e1
Alfrey-Price Qe値に関しても、情報化学を用いた推算式を構築しておく。
Alfrey-Price Qe値の推算
ニューラルネットワーク法を用いてQe値を推算するWebアプリを作成した。
有償のPro版に搭載。
重合シミュレーション
Alfrey-Price Qe値を用いたシーケンス解析ソフトPOSEIDON
POSEIDONのシミュレーション結果
Qe値の決定法
実験データがある場合、片方のモノマーのQe値が既知であれば、他方のQe値を決定することができる。仕込み濃度や重合度が異なる数点のデータ（NMR, 元素分析などでポリマー中の存在比率のデータ）が有れば良い。
自社のシステムに最適化されたPOSEIDONに進化させるには必須のプログラムである。
Pirikaの他のページ
MAGICINAページ、ポリマー設計と重合シミュレータ -POSEIDON-MTC3a
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。