2018.6.20
11. 臨界点から見た蒸発現象、そして沸騰現象
物質の状態
圧力の低い状態では、物質は密度の高い固体の状態、もしくは密度の低い気体の状態で存在しています。そこで、固体の場合には、結晶構造の規則性に注目し(分子運動による乱れはすくない)結晶格子モデルから検討が行われます。逆に、気体の場合には、不規則な分子運動に着目した理想気体モデルから検討が行われています。圧力が高くなってくると、3番目の状態である液体の状態が現れます。
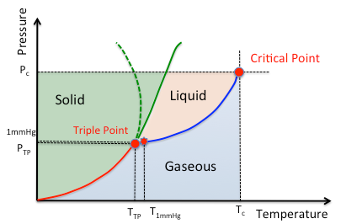
図11-1. 物質の状態図
炭酸ガスや一部の化合物は温度の上昇によって液体状態を経ずに、固体から気体へと状態変化します。この現象を昇華と言います。この昇華現象は特別な事と考えがちですが、圧力が3重点の圧力以下であれば全ての化合物は昇華します。逆に圧力が3重点以上であれば炭酸ガスでも液化させる事は可能となります。炭酸ガスの3重点は,-56.6℃、0.518MPaですので,炭酸ガスの固体,ドライアイスは大気圧(0.101MPa)では液体状態を経ずに気体になります。つまり「昇華」という言葉は,あくまでも地球基準であって,火星,木星では通用しないという事です。
固体が融解して液体になる際の体積変化は、蒸発による液体から気体への体積変化と比べ非常に小さいのが普通です。そこで融解のエントロピー(乱雑さ)も低く、蒸発潜熱に比べ、融解熱が小さい事の原因になっています。それは、圧力の低い,温度の低い状態下では、液体分子の持つ運動エネルギーは、固体の持つ運動エネルギーに近い事を意味します。
圧力の低い状態下と言っても、3重点の圧力より低ければ、液相は存在しませんので下限は3重点の圧力です。臨界点以上では、やはり液相は存在できないので、上限は臨界圧力です。3重点では、固体、液体そして気体が平衡状態で存在します。固体が存在できる以上、3重点の温度は融点に非常に近くなります。この融点という温度は、分子の形状、極性、パッキングのしやすさなどで大きく変化するので測定や推算が難しいので、(T1mmHg, 1mmHg)を3重点の代わりに採用した事は前章で述べました。我々が見る様々な液体(地球基準の25℃、大気圧下)の運動エネルギーは、多くの場合、(T1mmHg, 1mmHg)により近く、(臨界温度[Tc], 臨界圧力[Pc])からは遠くなります。25℃での蒸発を考えるなら、基準点は(T1mmHg, 1mmHg)に置くのが妥当です。沸点や、1気圧以上の高い圧力での蒸発を考えるのであれば、分子の運動エネルギーの観点から、基準点は(Tc, Pc)に置く方が妥当になります。そこで、この章では、臨界点から見た蒸発現象を見ていきましょう。
この固体—液体の状態変化に関しても、水は非常に残念な化合物です。液体は一般的には温度が下がると密度が高くなります。ところが、液体としての水は、約4℃で密度が一番高くなります。それ以下になると水素結合の構造体を生成し始め、逆に密度は低くなり、0℃になると結晶化が進み、固体の水の密度は液体の水と比べ約10%小さくなります。固体のほうが液体よりも密度が低いのはかなり珍しい物質です。氷は非常に規則正しい結晶を作るのでエントロピー(乱雑さ)は小さくなります。そこで、氷を溶かすには、そのエントロピー分大きな熱量が必要になります。風邪をひいて熱がある時に、氷枕を使うのは、体から大きな熱量を奪う必要があるからです。ただし、それは融解熱をKJ/Kgで見た時であって、KJ/molで見た時には通常の有機溶媒の中では小さな値になります。これは、氷から溶けたての水はまだエントロピーが十分高く無い事と、水の分子量が18と非常に小さいので、Kgあたりのmol数が非常に大きいからです。
臨界点
臨界点の定義は様々なものがあります。物理屋さんの定義,数学的な定義,化学工学,伝熱工学,機械屋さん的な定義,それぞれの分野で様々な言い方があるようです。数学が苦手で化学の道に進んだ私としては,数式ではなく,化学の基本中の基本,「現象の観察」から理解する臨界点を考えて見ましょう。前節で述べたように、固体から液体へ状態変化した直後は、液体の密度は固体の密度と大きくは変わりません。この液体をどんどん加熱していくと、液体の密度は液体の温度が高くなるにつれ下がって行きます。液体の密度は分子量/分子体積で計算できる事は前章で説明しました。密度が下がるという事は分子体積が大きくなるという事でしたが、分子体積が物理的に大きくなるのでは無く、分子の熱振動の為に分子が占める空間の大きさが温度の上昇と共に大きくなるという事でした。
この原理を使ったのが,体積温度計です。数千年の昔でも,長さを測る(主には人間の標準的な大きさを利用した)尺度や時間を測る(日の出から日没を利用した)尺度は,全世界にありました。水が凍ったら冷たい。水が沸騰していたら熱い。これは全世界で共通にあった事でしょうが,それを分割して体温に36という数字を与えるのは,長さや時間と比べて非常に難しいことであったでしょう。古代エジプトのアルキメデスの時代には温度計らしき装置がありましたが,現代の温度計に類するものは,ルネサンス期にガリレオが発明した気体温度計が最初とされています。
気体,水銀やアルコール,熱で膨張させるものは色々ですが,均質な太さのガラスの細管を作るのが難しかったので近代まで温度計が作れなかったようです。
それでは,温度が高くなるにつれ下がっていく密度はどこまで下がるのでしょうか? いわゆる標準沸点というのは、地球の都合でした。そこで、適当な圧力をかけていれば、液体は沸騰せずに温度は高くなり、密度は下がり続けます。液体の温度がある限界(臨界温度)に達すると、密度の値も限界(臨界密度)に達します。臨界温度では、分子の熱振動によって空間に占める大きさが臨界体積(分子量/臨界密度)となります。一方、気体の密度はどうでしょうか? 液体の温度が高くなるにつれ、気相に飛び出す分子の数が増えるので、気相の容積が一定なら気体の密度は、温度の上昇とともに高くなって行きます。気相では密度が高くなっていき、液相では密度が小さくなっていき、臨界点では両者の密度は一致します。つまり、液体と気体の密度の境がなくなるのが臨界点です。臨界温度以上の熱エネルギーを与えていると、どんなに高い圧力を与えても、液相は現れません。分子には、(惑星の重力のように)分子の大きさ、重さなどに従った、“集まろうとする力”、分子間力が働いています。この分子間力と熱振動のエネルギーが釣り合うのが臨界点です。そこで臨界温度以上の熱エネルギーを与えてしまうと、分子が部分的に集まる(液体状態)、分子間力>熱エネルギーの領域がなくなるので、どんなに圧力をかけても液相は現れないのです。
また、臨界圧力以上では、液体はどんなに加熱しても沸騰はしません。沸騰というのは、液体分子の運動エネルギーが外圧を上回った時に見られる「液体の激しい蒸発現象」です。臨界圧力以上の圧力がかかっている場合には、加熱によって与えられたエネルギーは、分子の熱振動エネルギーに使われますが、この分子のエネルギーが外圧を上回るのは、温度が臨界温度以上になる必要があります。臨界点を超えた段階で、液相と気相の境は無くなってしまうので、液体自体が存在しないので、液体の激しい蒸発現象は起こりえません。
この臨界点は、分子間力との関数なので、分子によって値はまちまちです。分子の大きさ、形状、分子を構成する原子団の種類などによって臨界点の絶対値はみな異なります。分子間力と臨界定数が釣り合った状態という意味では、臨界定数を分子の基準にとると、分子の差異を吸収できます。そこで物性値の理解には非常に有効であると言えます。このように有用な指標なのですが、実はこの臨界定数が実験的に求まっている化合物は1000化合物に満たないのです。測定法は、窓付のセルに化合物をいれ、温度、圧力を高くして、液相と気相の境が無くなる温度、圧力を探します。簡単そうに思えるかもしれませんが、場合によっては、化合物を少量抜き出したり、加えたりして(もしくは容積可変セルの利用)、液相—気相の境をセルの窓の位置に持ってこなければならいないなど、非常に困難な測定になります。また、分子が大きくなると、臨界温度も高くなり、高温を安定化させる事の困難さ、化合物自体の熱安定性の問題などから実験値は、この先、多くは増えないでしょう。
臨界点とPVT線図、臨界軌跡
臨界定数を測定する際に得られる、温度、圧力、密度(分子量/分子体積)をプロットしたものを、PVT線図と呼びます。多くの場合、X軸にV(体積)、Y軸にP(圧力)をとり、温度を一定にした時の(P、V)点をプロットする、を、温度を変えながら繰り返して行きます。一例としてエタノールのPVT線図を図11-2に示しましょう。
各連続する線は25℃おきの一つの温度を示します。
一番上の赤い線は、温度が600Kの時の圧力(P)-体積(V)関係を示します。温度がエタノールの臨界温度以上なので、圧力が高くても液化はせずに、超臨界流体と呼ばれる流体になります。
液体と気体が共存する領域は黒い線で示しています。全てが液体の領域は黄色の線で示しています。状態変化を温度、400Kで説明しましょう。耐圧性の容積可変セルに400Kのガスを詰めると①の状態になります。そのセルを、温度を保ったまま圧縮して行くと状態②で、ガスの一部が液化し始めます。さらに圧縮して行くと気液が混在している間は、圧力は一定になります。全てが液化すると、液体は圧縮しても体積はほとんど変わらず圧力だけが急上昇して④の状態に達します。これは逆向きに動かしても同じことです。温度を400K, 450K, 500Kと高くして行くにつれ、気液が混在する(黒い線の部分)が短くなって行くのが解ると思います。温度が514Kになると、気体と液体の区別がなくなり、臨界点に達します。この臨界点から気液混在の黒い線の両端をつないだ紫色の線を臨界軌跡と呼びます。
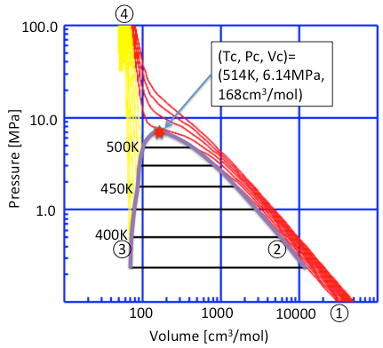
図11-2. エタノールのPVT線図
同様にヘキサンのPVT線図を作成します。
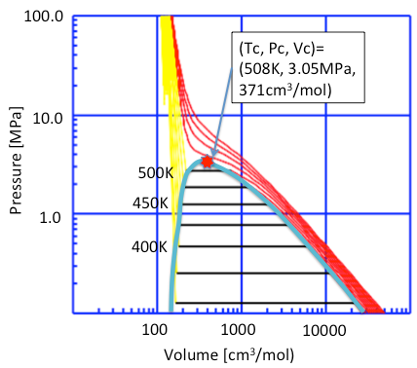
図11-3. ヘキサンのPVT線図
エタノールとヘキサンでは臨界点の絶対値は異なります。
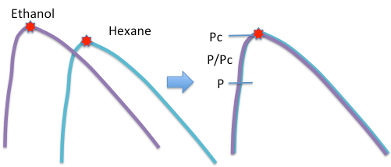
図11-4. 臨界軌跡の一致
しかし、臨界軌跡を取り出し、臨界点を重ねると軌跡はほぼ完全に一致します。従って、様々な化合物の分子としての基準点を臨界点にとり、各物性値が臨界点からどれだけ離れているかで評価できれば、化合物の違いを吸収できる事になります。前章では,25℃での相対蒸発速度は還元圧力(25℃での蒸気圧/臨界圧力)のみに依存することを示しました。これは,臨界圧力も25℃での蒸気圧も化合物によって値は異なりますが,臨界軌跡は一致しているので,還元圧力が同じであれば相対蒸発速度も一致するということを意味します。この基準点からどれだけ離れているかを示す尺度を対臨界値といいます。温度を臨界温度で割った値を還元温度、圧力を臨界圧力で割った値を還元圧力、体積を臨界体積で割った値を還元体積と呼びます。各々の絶対値は異なりますが、比率にしてしまえば、どのような化合物でもスケールも含め一致するので非常に扱いやすくなります。この方法で物性値を見るやり方を「対応状態原理法」といいます。それでは、蒸気圧を例に対応状態原理法をみてみましょう。
対応状態原理法による蒸気圧式
まず簡単な例として、標準沸点(Tb, 0.1MPa)から臨界点(Tc, Pc)の間の任意の温度(Tref)での蒸気圧(Pref)を求める蒸気圧式を作成してみましょう。
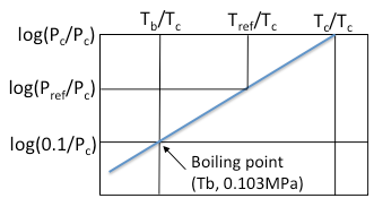
図11-5. 対臨界値蒸気圧式
中学生でも解るようにグラフで考えてみましょう。各温度、圧力は絶対値では扱わないで対臨界値で扱います。蒸気圧は図中の青い線で示されているので、この青い線の数式を求めます。直線の一般式は
Y=aX+b
でaは傾きですから、a=(log(Pc/Pc) – log(0.1/Pc))/ (Tc/Tc – Tb/Tc) = (1+ log(Pc)) / (1- Tb/Tc) となります。
式のYにlog(Pc/Pc)=0, XにTc/Tc=1を代入すると、b=-aとなるので、
log(Pref/Pc)= -a*(1-Tref/Tc)
a=(1+log(Pc))/(1-Tb/Tc)
上記の式を使うと、化合物の標準沸点(Tb)、臨界温度(Tc)、臨界圧力(Pc)が求まっていれば、任意のTrefの時の蒸気圧Prefが求まります。
前章のAntoineの蒸気圧式で検討した液体について、蒸気圧を見てみましょう。
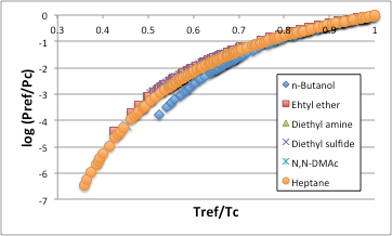
図11-6. 対臨界温度に対する対臨界圧力
この蒸気圧式は、標準沸点から臨界点までの蒸気圧が直線で近似できるという前提で作った式です。
ここで、Tref/Tcが0.70から1.0の間では液体の種類によらずによく一致していることがわかると思います。多くの化合物で、Tb/Tcは0.68ぐらいですので、沸点から臨界点までの蒸気圧は直線近似しても大きな間違いは無い事になります。温度が沸点以下になると、急激に蒸気圧は減少します。このままだと扱いにくいので、昔の人は、前章で使った蒸気圧式のうちで一番シンプルなClausius-Clapeyron式を使う事にしました。
log(P)=A – B/T
ここでも、各温度、圧力は絶対値では扱わないで対臨界値で扱います。標準沸点(Tb, 0.1MPa)と臨界点(Tc, Pc)を通る条件から、
log(Pref/Pc) = h*(1 – 1/(Tref/Tc))
h=(Tb/Tc)*log(Pc) / (1- (Tb/Tc))
という、一般化蒸気圧式が得られます。
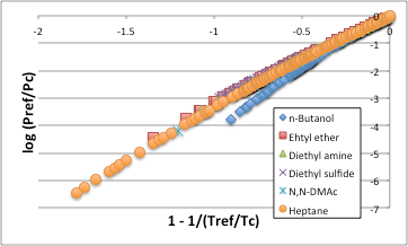
図11-7. 一般化蒸気圧式
この一般化蒸気圧式を使って、横軸を(1-1/(Tref/Tc))としてプロットすると図11-17に示すように曲線は、ほぼ直線になります。しかし、ブタノールのような水素結合性の液体は他の液体とは挙動が異なります。Antoine式ではAntoine B定数(蒸発潜熱)で補正がかかっていました。一般化蒸気圧式では偏心因子という新たなパラメータを導入して補正をかける方法が取られました。
偏心因子
偏心因子ω(Acentric factor)は1955年にPitzerによって定義されたパラメータです。
ω = -log Pvpr ( at Tr=0.7) -1.0
で 計算される値で、Pvprは, (Tr=0.7となる温度における蒸気圧)/臨界圧力になります。偏心因子を実験的に得る為には、沸点、臨界温度、臨界圧力、Tr(=Tref/Tc)=0.7となる温度における蒸気圧の実験値が必要になります。このパラメータが提案されたときには、偏心因子は単に分子の偏心性や非球形度を表すものとされていました。そこで、単原子ガスやメタンなどでは偏心因子は、ほぼゼロになります。分子が大きくなったり、極性があがると偏心因子は大きくなるので、幾何学そして極性的な中心からのずれを示すパラメータとして重宝されています。
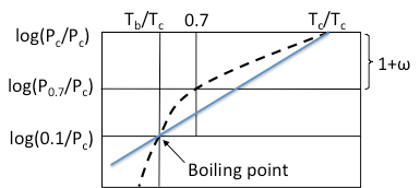
図11-8. 偏心因子の定義
グラフ中に定義の点を書き込むと理解が深まるでしょう。多くの液体では対臨界温度Tr(Tref/Tc)が0.7となる温度は沸点以上です。ですから、(沸点、1気圧)、(Tr=0.7、Pvpr),(Tc、Pc)の3点を通る蒸気圧曲線にする事で、曲率を補正するパラメータであることが解ります。一般化蒸気圧式に偏心因子を組み込んだ形で利用できると、利用価値が高いのですが、不勉強ながら、そうした式にはお目にかかった事はありません。その理由の一つは、沸点以上、臨界点以下の蒸気圧式は直線近似しても大きな違いは無く、室温以上沸点近傍の蒸気圧はAntoine式などを使えば十分精度がたかいので、一般化蒸気圧式に組み込む必要が無かったのではないかと思います。ちなみに、Antoine C定数も分子が大きくなったり、極性があがると大きくなる定数である事を前章で紹介しました。
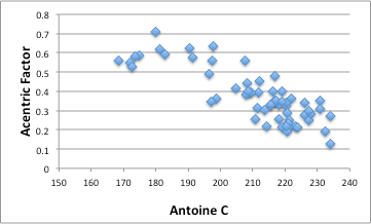
図11-9. Antoine Cパラメータと偏心因子の関係
そこで、Antoine C定数に対して偏心因子をプロットすると図のように高い相関がある事がわかります。そこでどちらのパラメータも分子の分子間力を考察する上で重要なパラメータであると言えます。
偏心因子が一般化蒸気圧式に組み込まれなかったもう一つの理由は解析的な計算式の発展があげられます。
一般化蒸気圧式は、任意の対臨界温度Tr(Tref/Tc)の時の対臨界圧力Pr(Pref/Pc)を求める事ができます。そこで、Tr=0.7の時のP0.7/Pcも計算できます。
log(P0.7/Pc) = h*(1 – 1/(0.7))
h=(Tb/Tc)*log(Pc) / (1- (Tb/Tc))
ω = -log (P0.7/Pc)-1.0
から
ω = (3/7)*h -1
となります。この偏心因子の事を、Edmister(1958年)の偏心因子と呼びます。
このEdmisterの偏心因子は、炭化水素化合物の(実験から求めた、Pitzerの)偏心因子とよく一致した事から、非常に大きな
混乱が現在まで続いているのです。
我々は、未だに分子間に働く力を全て理解しているとは言えません。ましてや、その分子間力の温度依存性まで含めると多くを語れないのです。Pitzerの偏心因子は、その個々には分割できない分子間力の総和を実験値の蒸気圧測定から決定するものです。それに対してEdmisterの偏心因子は、沸点、臨界温度、臨界圧力のみから求まる値です。複雑な分子間力が沸点、臨界温度、臨界圧力に反映されている場合には両者は一致しますが、図に示しますように必ずしも一致するとは言えません。
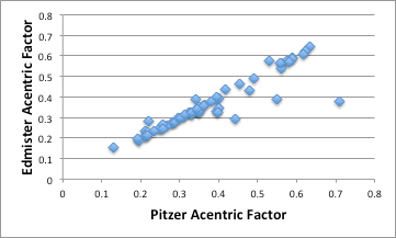
図11-10. PitzerとEdmisterの偏心因子の関係
ところが、Edmisterの成功以来、偏心因子は臨界値から求めるものになってしまいました。臨界定数から蒸気圧を推算する式としては、
Riedel法(1954年)
Riedel-Plank-Miller法(1965年)
Lee-Kesler法(1975年)
などがあります。
Lee-Keslerは次式で偏心因子を計算します。(Tbr=Tb/Tc)
ω = f(0)(Tbr)/f(1)(Tbr)
f(0)(Tbr)= -ln(Pc) -5.92714 +6.09648*Tbr-1+1.28862*ln(Tbr) – 0.169347*Tbr6
f(1)(Tbr) = 15.2518 -15.6875*Tbr-1 – 13.4721*ln(Tbr) + 0.43577*Tbr6
非常に複雑な計算式ですが、単純なEdmisterの偏心因子と比較してみると、ほとんど完全に一致してしまいます。
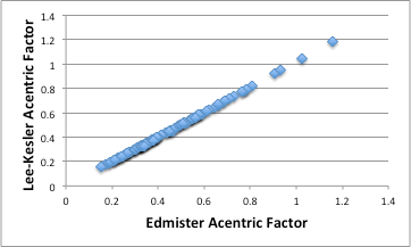
図11-11. EdmisterとLee-keslerの偏心因子の関係
そこで、Lee-Keslerの蒸気圧式
ln(Pref/Pc) = f(0)(Tr) + ωf(1)(Tr)
で蒸気圧を計算したとしても、複雑な分子間力を全て取り込めているとは言えません。(Pitzerの実験値から求めた偏心因子との差分は残ってしまいます。)
詳しくは筆者のHP(https://www.pirika.com/JP/TCPE/VP-Theory.html)
を参照頂きたいのですが、Riedel式では偏心因子と言う言い方はしていませんが、αcというパラメータを定義しています。これも、沸点、臨界温度、臨界圧力から計算されるパラメータとなります。
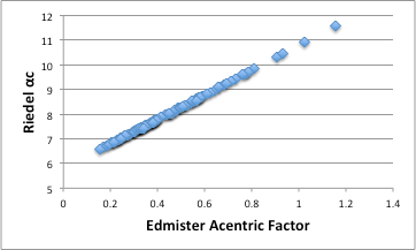
図11-12. Edmisterの偏心因子とRiedelのαcの関係
このパラメータもスケールは異なりますが、Edmisterの偏心因子と実質同じ物になります。
以上の事を踏まえると、対応状態原理法を用いた蒸気圧式は、複雑な分子間力が沸点、臨界温度、臨界圧力に反映されている場合、もしくは、沸点以上の温度域ではそれなりの精度が期待できますが、それ以外の場合には闇雲に信じてはいけないことが解ります。
しかも、臨界定数の正確な測定値は今後大きく増える事は期待できないので、精度の高い推算方法の開発が必要になります。
臨界定数の推算
臨界定数の推算法は様々なものがあります。加算値など詳しいことは筆者のHPに譲るとして、ここではJoback法という原子団寄与法による推算法を見て行きましょう。Dr. Jobackは1984年、MITの学生のときに臨界定数などの推算式を開発し、現在でも広く使われています。(Dr. Jobackは私の個人的な友人でもあり、物性推算式の更なる精度向上を目指しながら議論を行なっています)
Joback法は次式によって臨界定数を計算します。
Tc = Tb[0.584 + 0.965ΣΔTc – (ΣΔTc)2]-1
Pc = (0.113 + 0.0032NA – ΣΔPc)-2
Vc = 17.5 + ΣΔVc
ΔTc、ΔPc、ΔVcは、各原子団に割り振られた加算値です。分子を構成する原子団を数え上げ、その個数に加算値を掛け合わせて、その総和を計算します。Tbは標準沸点、NAは分子を構成する原子数の総和を示しています。そこで、分子の構造と標準沸点が得られていれば臨界定数が得られる事になります。
それでは、まず、臨界温度の意味合いを考えて見ましょう。Joback式では臨界温度=沸点*(原子団の寄与)となっています。そこで、Tc/Tbがどんな物性値と相関があるのか調べて見ます。まず、水素原子を含む原子の総和とプロットして見ましょう。
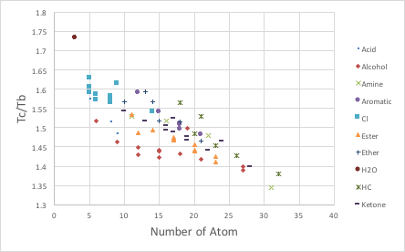
図11-13. 分子中原子数とTc/Tbの関係
Tc/Tbの平均はおおよそ1.5になり、分子を構成する原子の数が多くなるほど、Tc/Tbの値は小さくなります。そこで、原子数の効果は逆数で効いています。分子が持つ官能基の種類が決まれば(例えばエステル化合物)原子の数が多くなるにつれ直線的にTc/Tbの値は減少するので、エステル基の寄与率を定めれば、原子団寄与法で臨界温度(Tc)が推算できることになります。正確には、式の形を見ればわかるように、2次関数の上に凸で近似しているのがJoback法の臨界温度推算法であることがわかります。それでは、アルコールやカルボキシル化合物でTc/Tbが小さいというのは何を意味するのでしょうか? 沸点の割に臨界温度が低い(もしくは、臨界温度の割に沸点が高い)ことを意味していて、これはとりも直さず、沸点よりも高いところに屈曲点を持つということを意味します。その屈曲率の大きさとは、前節で説明した偏心因子と同じ事になります。
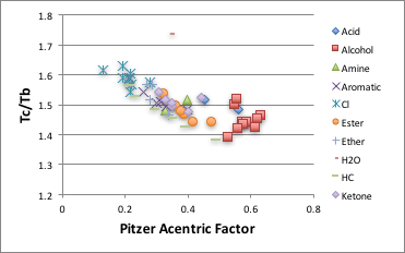
図11-14. Pitzerの偏心因子とTc/Tbの関係
そこで、実験値から求めたPitzerの偏心因子に対して、Tc/Tbをプロットすると図に示すようなVの字型の関係が得られます。
予想したように、かなり良い相関があります。前章で説明した正則溶液に関しては化合物の種類によらず、偏心因子が(0.5ぐらいの所まで)大きくなるにつれ、Tc/Tbは直線的に減少する事がわかります。この領域に関しては、偏心因子の持つ意味合いの一つである球形からのずれが大きくなるとTc/Tbが小さくなって行きます。例えば、C5H12で表されるペンタンの異性体を見てみましょう。n-ペンタン(CH3CH2CH2CH2CH3)では、Tc/Tb=469.8/309.2=1.519、イソペンタン(CH3CH(CH3)CH2CH3)では、Tc/Tb=460.4/301.0=1.530、ネオペンタン(C(CH3)4)では、Tc/Tb=433.8/282.7=1.534となります。同じ原子数ですが、分子の枝分かれが多くなるにつれて沸点や臨界温度は小さくなります。しかし、沸点の減少分が少し大きいので、Tc/Tbは大きくなって行きます。
偏心因子が0.5以上となる化合物は、アルコール化合物やカルボキシル化合物になります。これらの化合物は、水素結合によって非正則溶液(水素結合を切るために多くの蒸発エネルギーが必要)になる液体です。正則溶液は分子が大きくなると偏心因子が大きくなりましたが、非正則溶液では、逆に分子が小さくなると偏心因子が大きくなります。そして、偏心因子が大きくなると、逆にTc/Tbが大きくなります。この領域では偏心因子の別の側面、極性の偏りの効果によって引き起こされます。
このトポロジカルな偏心性と極性の偏心性を一つのパラメータωに押し込んでいるので、とても複雑なパラメータである事がわかります。
水、メタノール、ギ酸などは、分子が小さく、球形に近く、極性でもあるのでV字型の線からは大きく外れます。
大事な点は、環状化合物の特異性です。正則、非正則溶液の違いだけでなく、先ほどのV字に乗らない化合物としては、環状エステル、環状アルコール等の環状化合物などがあります。これらの環状化合物には、何らかの分子間力が働いて、Tc/Tbの値が鎖状化合物と異なってきます。その事が何を意味するかというと、Jobackの加算値でこうした環状化合物を計算しても高い精度は期待できないということです。それは、Joback法では環状のエステル基、2級の水酸基の加算値が定義されていないからです。物性推算式は、その推算式を構築した時の母集団に依存します。母集団に類似の化合物を計算する場合はそれなりの精度が期待できますが、どんな化合物に対してもオールマイティーに精度が高い推算式というのは、まだまだ難しいのが現状です。実験値の偏心因子を使えば回避できる問題ですが、偏心因子自体を臨界定数から計算で出した場合には、誤差が増幅される可能性があることを考慮しなくてはなりません。
臨界圧力の推算に移りましょう。
Joback法の臨界圧力推算式では、水素を含む全原子数(NA)と原子団の加算値(ΔPc)の総和で臨界圧力が計算されます。推算式によっては、重原子だけ、分子量などと相関づけたりしていますが、基本的には分子が大きくなると臨界圧力は緩やかに小さくなる事がお分かりいただけるでしょう(図11-15)。
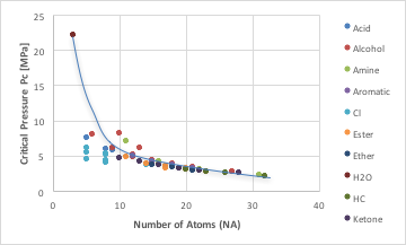
図11-15. 重原子数と臨界圧力の関係
大きく外れているのはNA=3の水です。そしてアルコールやアミン、塩素化合物が曲線から外れます。塩素化合物は同じ原子数なら塩素の数が多いほど臨界圧力は小さくなります。曲線から外れた分を原子団の加算値(ΔPc)で補正するのがJoback法です。分子の運動論的に言えば、分子が大きくなると分子量がふえ、動きにくくなり壁との衝突も減ります。分子同士の衝突も増え、圧力として観測される正味の量も減ることになります。分子中の塩素の数が増える効果は分子量の効果で解釈できます。水素結合性化合物の臨界圧力が高くなる事は、水素結合を切るために臨界温度も高くなる効果との兼ね合いになるので非常にむずかしい問題になります。
つまり、ハロゲン原子を持つアルコールの臨界圧力がいくつになるかは予測できないことになります。
そうした時に有効な考え方を示しておきましょう。横軸を25℃での分子体積に変えてみます。すると塩素化合物の特異性は消え去る事がわかります。つまり、Joback法で全原子数(NA)という時には、周期律表で第2周期の原子までのことで、第3周期の塩素は、せいぜい分子中に1つ程度の時に成立するだけなのです。炭素と塩素を同じ原子数1と数えると、塩素化合物が曲線からずれてしまいます。しかしファンデルワールス半径が塩素は20%増しと考えれば、他の原子と区別して考える必要は無くなります。他の指標としては分子量も考えられますが、塩素は炭素の300%増しとなり、かえって整理がつかなくなります。
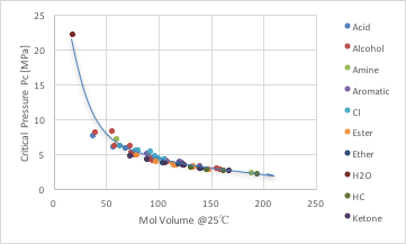
図11-16. 分子体積と臨界圧力の関係
そこで、分子体積を元にした新たな推算式を構築し、他の推算式とクロスチェックをする事によって徐々に精度をあげて行くという地道な作業をDr. Jobackと行なっています。
最後に臨界体積の推算です。
Joback法の臨界体積推算式は非常にシンプルな原子団寄与法です。各原子団に割り振られたΔVcの総和に定数を足すと臨界体積が得られます。臨界温度、臨界圧力と比べると物性値として重要度が低いと思われがちで、混乱している物性値です。実測値として得られるのは臨界密度です。分子量(MW)が判っているのでMW/臨界密度が臨界体積になります。これを“計算値の臨界体積”と呼んで記載する場合と、原子団寄与法で計算して“計算値の臨界体積”と呼ぶ場合、単に臨界体積と呼ぶ場合があるようです。
先ほども触れましたが、推算式はそれを構築したデータベースの値に強く依存します。その値があやふやさを含んでいる場合、得られた推算式の精度も高くなりようがない事を覚えておく必要があります。また、臨界体積は物性値として重要でないというのも認識を改める必要があります。密度の温度依存性は臨界密度が一つの終点です。密度は表面張力、粘度、熱伝導率の物性値とその温度依存性に大きく関与してくる物性値なのでとても重要な指標です。25℃での分子体積と臨界体積をプロットすると図11-17のように高い相関がある事がわかります。ざっくり言えば、25℃での分子体積の3倍が臨界体積になります。今まで見過ごされていましたが、実はこれは非常に示唆に富む事実なのです。液体の密度は25℃から温度を上げていくと徐々に下がっていきます。臨界温度の値は液体の種類によって異なります。25℃から高い臨界温度(例えば400℃)まで落ち続けても、低い温度(例えば190℃)で臨界温度に達しても密度は何時も25℃の時の1/3となると言っているわけですから是非不思議に思っていただきたい所です。
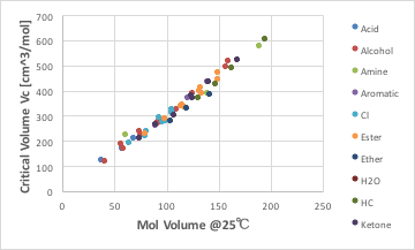
図11-17. 25℃における分子体積と臨界体積の関係
液体分子体積が温度の上昇と共に大きくなるのは、分子が大きくなるのでは無く、分子運動が激しくなって、分子が占めている空間が大きくなる事であるとは、前に説明しました。その空間が25℃の時の3倍になると、臨界点に達するのです。気体は温度が高くなると圧力がどんどん高くなるので、密度が高く(分子体積は小さく)なっていきます。そして、その気体の占める空間が25℃液体の時の3倍になると、気体と液体の密度が一致して臨界点として観測されるのです。水は小さな分子なので、体積で見ると3倍にはなりませんが、臨界密度は0.322g/cm3なので密度的には25℃の1/3になります。
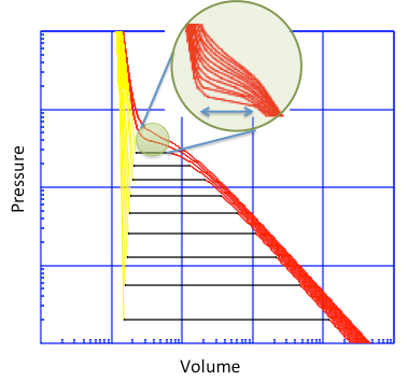
図11-18. 臨界点における体積に対する圧力の変化
この臨界点では、体積に対する圧力の変化の傾きがゼロになります。臨界点近傍を拡大して示します。各線は1℃刻みの温度を示します。この領域では圧力、温度がほんの少しゆらぐだけで、体積が大きく変化します(そこが、測定が非常に困難である由縁です)。様々な化学反応速度、熱物性値、溶解性が劇的に変化する領域なので“ミラクル・デンシティー”と呼ばれています。
その領域でどのような事が起きているのかの一例を示しましょう。化学者の“認識“として臨界点でどのような事が起きているかの理解が深まると思います。
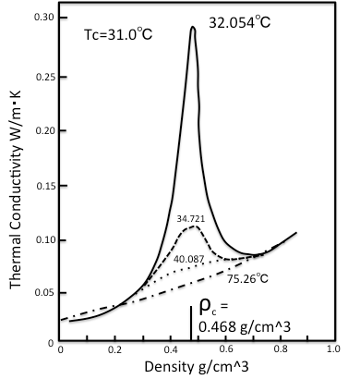
図11-19. 炭酸ガスの密度と熱伝導度の関係
二酸化炭素の臨界点近傍での熱伝導率の変化を図11-19に示します。二酸化炭素の熱伝導率は臨界点近傍で急に大きくなります。これは臨界発散と呼ばれる現象です。気体の熱伝導率は液体の熱伝導率の1/10ぐらいになってしまいます。それは気体がスカスカで熱の高い(運動エネルギーの高い)分子が他の分子にぶつかってエネルギーのやり取りをする確率が低いからです。それでは超臨界状態では、何故、液体よりさらに熱伝導率が高くなるのかと言うとビリヤードみたいなものと説明されています。ビリヤードで最初にブレークする時には一つのボールを強く突きます(熱の高い分子)。それが十分長い距離走って10個のボールの固まりにぶつかるとエネルギーの授受が行われ10個は弾け飛びます(熱の高い分子から熱伝導して高い熱を持った分子へ)。その際に10個が互いにくっついているときれいにブレークできますが、一部はなれていたりするとうまくいきません。水素結合性の液体の熱伝導率が他のものと比べ高いのは、分子がくっついているからと説明されます。ボールがうじゃうじゃいる所(液体)でボールを強く突くと他のボールにはスピードが伝わらず弾き上がってしまいます。(気体になってしまう)そんなわけで臨界点近傍では熱伝導率は非常に高くなると言われています。この助走区間が臨界点では、平均すれば25℃での分子体積の3倍であること、密度揺らぎが非常に大きく、濃いところと薄いところのある雲のような形で存在しているのが臨界状態の分子の姿と言えるのでしょう。こうした熱伝導率の高さ(除熱のしやすさ)、溶解性を利用してフッ素系のモノマーを重合する超臨界重合が実用化されています。
超臨界炭酸ガスというと何かすごく特別な存在のように思えるかもしれません。しかし、中を見ることはできませんが、炭酸ガスの消化器は温度が31℃を超えれば、中身の炭酸ガスは臨界点に達します。夏場には簡単に超臨界炭酸ガスになるので、消火器を日向に置くのはやめましょう。ちなみに、47℃に達すると 15.7 Mpa の圧力になるので安全板が破裂し、中身が吹き出します。
次には、臨界定数と、沸騰に関係する物性を見て行きましょう。
沸騰現象については、私は専門家では無いので甲藤先生の「沸騰の科学」を利用させていただきます。
気泡核の発生
液体をビーカーのような入れ物に入れて加熱を始めると、液体の温度が上昇して、やがてビーカーの底の方に泡が発生します。
「その時の温度が沸点である」というのは間違いである事が甲藤先生の著書に記載されています。泡が発生するには、沸点より少し高い温度が必要になります。沸点とは蒸気圧が1気圧に達する温度ですが、液体の中では表面張力が働いているので、その表面張力に打ち勝つだけ、少し高い温度が必要になります。
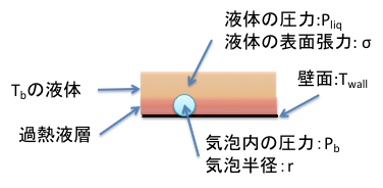
図11-20. 気泡核の発生
その時の気泡核の半径(r)と、表面張力(σ)、圧力差(ΔP)は次式で示されます。
ΔP=Pb – Pliq = 2σ/r
r = 2σ/ΔP
表面張力の高い液体は同じ圧力差をかけた場合でも、気泡核の半径は大きくなり、ビーカーの底の大きな凸凹からしか沸騰でなくなるそうです。そこで、場合によると突沸(沸点より十分高い温度に達した液体が何かのショックで突然激しく沸騰する現象)を起こしたりします。表面張力が低い液体は逆にビーカーの底全面から細かい泡が発生することになります。
液体の圧力差がいくつになるかは、前章のAntoine式やこの章の蒸気圧式のところで説明した式に沸点(Tb)と過熱分(Tb+ΔT)を入れれば簡単に計算できます。次に液体の表面張力を説明しましょう。特に大事なのは表面張力の温度依存性の問題です。例として沸点がほぼ100℃の8種類の液体を見ていきましょう。
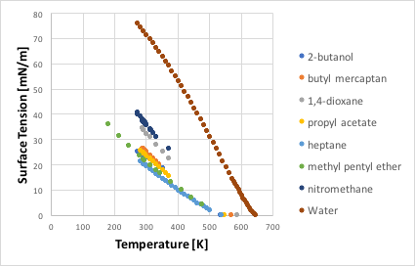
図11-21. 温度と表面張力の関係
図11-21に示しますように、どの液体も温度が上昇するに連れて表面張力は小さくなり、臨界温度に達した時に表面張力はゼロになります。水、ニトロメタン、1,4-ジオキサンなどは25℃で大きな表面張力を持ちますが、それ以外の液体は、アルコールであってもほぼ同じくらいの表面張力になります。臨界温度でゼロになる物性なので分子基準の温度に変換するために、横軸を(1-Tref/Tc)に変換します。グラフの原点(0,0)が(臨界温度, 表面張力=0)になります。
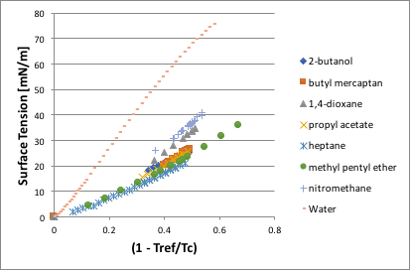
図11-22. (1-Tref/Tc)と表面張力の関係
水、ニトロメタン、1,4-ジオキサンが他の液体と合わないのは、臨界圧力のせいなので、さらにその補正を入れます。
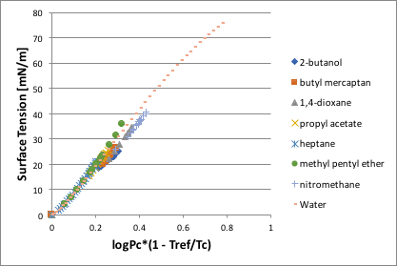
図11-23. log(Pc)*(1-Tref/Tc)と表面張力の関係
すると、水も含めて直線はほぼ一致します。
Surface Tension @Tref=100.72*log(Pc)*(1-Tref/Tc)-1.5305
で任意の液体の任意の温度での表面張力を得る事ができます。
つまり、液体の臨界温度と臨界圧力が得られていれば、任意の温度での表面張力の値が得られることになります。蒸気圧を得るのに必要な物性値も臨界温度と臨界圧力と沸点ですので、臨界定数と沸点が判っていれば任意のΔTの時の気泡核の大きさは予測できることになります。細かい差異は分子の形状によるものです。棒状の分子と球状の分子で差が残ってしまいます。
代表的な表面張力の対応状態原理推算法にはBrock-Bird法があります。
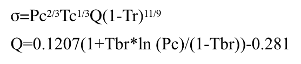
σ: 表面張力、Pc : 臨界圧力、Tc : 臨界温度
Tr : 還元温度、Tbr : 沸点/Tc
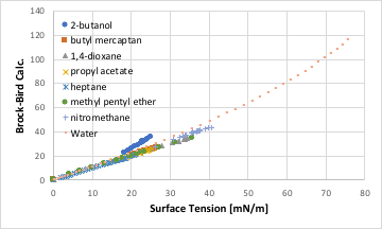
図11-24. Brock-Bird法による表面張力の推算
Brock-Bird法と比べると,今回作成した単純な式で良好に推算できることがわかると思います。大事な点は,前章で指摘した様に今まで25℃での表面張力が高い化合物を極性溶媒であると考えて来たのは間違いであるということです。25℃,1気圧が臨界温度,臨界圧力からどれだけ離れているかだけで,表面張力の値は決まるということです。いわゆる極性基が分子に導入されると,臨界温度が高くなるので,25℃での(1-Tr)が大きくなり表面張力が大きくなるだけということになります。
気泡核の成長
一旦泡ができると、その泡はどんどん成長を始めます。

図11-25. 気泡核の成長
図11-26. 液体の蒸発
液体の蒸発は基本的には、気相と接している部分から起こります。液体が液体として存在できる為には、その温度での熱振動より大きな分子間力を持つ必要があります。液体の内部では分子は周りを他の分子で取り囲まれているので、分子間力が一番強くなります。壁面、気相と接している面は分子間力が切れている状態になるので蒸発はそうした部分から起こります。つまり最初に気泡核ができると、その気泡に接している分子は分子間力が弱くなっているので気泡の中に蒸発していくので気泡が成長し始めます。
その蒸発のしやすさを決めているのが、蒸発潜熱です。この物性値を対応状態原理で考えてみましょう。単位がKJ/molであることに注意してください。化学工学や機械系ではKJ/Kgで扱う事が多いようです。
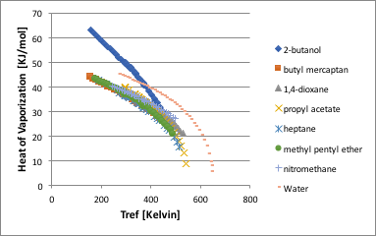
図11-27. 温度に対する蒸発潜熱の関係
蒸発潜熱も表面張力と同様に臨界点に達すると値がゼロになる物性値です。しかし、表面張力では液体によって交差することは無かったのですが、蒸発潜熱の場合には臨界点に向けて急激に値が小さくなるので曲線が交差する事があります。一見複雑に見えますが、先ほどと同様に横軸を(1-Tref/Tc)に変換するとスッキリします。
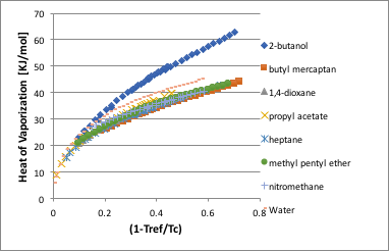
図11-28. (1-Tref/Tc)に対する蒸発潜熱の関係
この関係を使ってある温度での蒸発潜熱の値と臨界温度の値から,特定の温度での蒸発潜熱に変換するWatson式が開発されています。
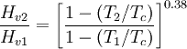
しかし,この式を使って変換して良いのは正則溶液だけです。Watson式の指数0.38は正則溶液の平均値だからです。
アルコールと水が大きく外れるのを水素結合の為と考えると、水の方が強い水素結合をするはずなので話が合わなくなります。実はこの違いは、臨界温度に向けて急激に蒸発潜熱が低下するその曲率に依存しています。そして,その曲率とは蒸気圧の項で説明した偏心因子に他なりません。
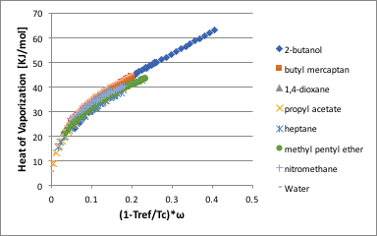
図11-29. (1-Tref/Tc)*ωと蒸発潜熱の関係
そこで、横軸をさらに偏心因子をかけて補正をすると全ての曲線はほぼ一致します。偏心因子も臨界温度、臨界圧力、沸点から計算できます。そこで臨界定数と沸点が判っていれば、任意の液体の任意の温度での蒸発潜熱は計算で出すことが可能になります。残りの細かい差は表面張力の時と同じで形状因子によるものと思われます。
任意の温度での蒸発潜熱を推算する対応状態原理法としてはPitzer-Carruth-Kobayashi 法が著名です。これは下式で蒸発潜熱を計算します。
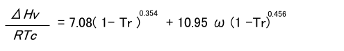
ΔHv : 蒸発潜熱 (KJ/mol) Tr : 還元温度 (T / Tc)
w : 偏心因子 R : 気体定数
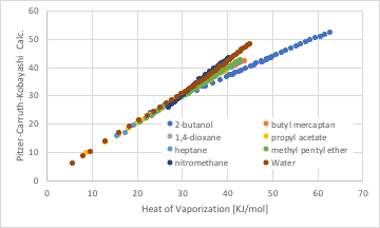
図11-30. Pitzer-Carruth-Kobayashi 法による蒸発潜熱の推算
Pitzer-Carruth-Kobayashi 法では値が大きな領域(測定温度が低い温度の時)の誤差は大きくなります。本来,偏心因子を用いれば低温での補正もされるはずですが,水,アルコール,ニトロメタンで,大きなずれが残ってしまいます。
例えば,沸点40℃の液体を70℃で蒸発させる時のことを考えてみましょう。コンピュータで総当たり的に分子を発生させる。そして沸点や臨界定数を予測し,沸点が40℃近辺のものを選択する。70℃の時の表面張力や蒸発潜熱を臨界定数から予測して,沸騰・蒸発しやすい構造を網羅的に得る。といった研究の進め方は1990年台には普通にやられていた研究方法です。前述のDr. Jobackの作成したSYNAPSEというソフトウエアーはそうしたことが簡単にできるソフトウエアーです。コンピュータの性能向上,ハードディスクの容量増加,ネットワークの高速化などによって,こうした研究手法はますます容易に行えるようになってきました。当時は「物性推算と逆設計」という言い方をしていましたが,今では「マテリアル・ゲノム」とか「マテリアル・インフォマティクス」という言い方をするようになってきました。Dr. Jobackとはさらに「プロセス・ゲノム」でプロセスまで含めてゲノム解析しようと研究を進めているところです。言葉は変わってもやらなくてはならない事は,先に説明したように化合物の違いをいかに吸収するか?を考える事です。もうしばらくすれば,そうした事はAIが勝手にやってくれる時代が来るでしょう。実際問題,私自身こうした推算式を考えるときには,完全自動とまでは行きませんが,自分で作ったニューラルネットワークのソフトに手助けしてもらっています。AIと仲良くして,AIアシストを最大限に利用できるようにするというのは私の授業での大事なコンセプトです。
次に移る前に,マイクロウエーブ(MW)による加熱・沸騰現象に触れておきましょう。MWによる加熱は目的によっては非常に優れた加熱法です。反応の収率や選択率が劇的に向上したりするのでグリーン・ケミストリーなどにも利用されています。甲藤先生の著書には、「MWで例えば水が加熱されるのは、水のダイポール・モーメントとMWの波長が一致するので、分子が回転してその摩擦熱で加熱される」というような記載があります。そうした説明では、例えば「メラミン樹脂の容器をMWで加熱するな」の理由を理解できません。メラミン樹脂は尿素基が多数結合したポリマーですので、回転できません。そこで回転による摩擦熱が発生することはありません。しかし、メラミン樹脂はMWをよく吸収して溶融・炭化します。通常のガラスはMWを吸収しませんが、銅やタングステンの酸化物は非常に良くMWを吸収します。そうした金属酸化物触媒はMWによって反応速度が非常に加速されます。このようにMWによる加熱は様々な要因が絡み合うので一言では説明できないものです。液体に限れば、「MWを吸収した分子中のある結合が標準結合長より長くなり、エントロピーが増大する。その結合長が元に戻るときに分子の熱運動に変換される」というのが一番近い表現になるのかもしれません。各原子がバネでくっついた分子から,一つの原子を引き伸ばし離すと,バネが元に戻る勢いで分子全体が激しく運動するといったイメージでしょうか?どの原子間ペアが引き伸ばされるのかというと,その結合のダイポールモーメントだったり,結合次数だったりします。氷がMWでは加熱できないのは,3次元的な水素結合のネットワークで見かけの結合数が多く,バネを引き延ばせないからと考えられます。
MW加熱は,液体の中心部を加熱するというもう一つの特徴が挙げられます。通常の加熱は高温の壁面などを通じての伝導伝熱です。図でも説明しましたように,壁面や気体と接した面では分子間力のネットワークが切れていて,そこから蒸発が始まります。液体の中心部はネットワークが一番強固なので一番動きにくい領域です。そこでMWを使って液体の内部から加熱をすると,標準沸点に達した後も気泡核を生成できない事があります。これをスーパーヒート現象と言います。酢酸やメタノールなどでは,沸点より20℃以上高い温度にまで達します。何かショックがあると爆発的に沸騰する突沸を起こすので注意が必要です。
気泡核の成長–その2
気泡に接している液体から蒸発潜熱を奪いながら気泡核が成長することは前節で説明しました。液体の側としては熱を奪われるので液体の温度は低下します。奪われる熱量は蒸発潜熱ですので,Q=Hv=比熱*ΔT分だけ温度が低下します。そのΔTが非常に大きかったりすると,液体の温度が沸点以下にまで冷却され,気泡核が逆に小さくなったり,場合によっては消失する事があります(凝縮顕熱を与える)。壁面から熱が入って来た時にどれだけ温度が上がるかも同じ式になるので,液体の比熱について考えてみましょう。まず、言葉の定義ですが、比熱と同じような意味に使われる熱容量という言葉があります。熱容量はある物質を、1℃温度をあげるのに必要な熱量を言います。そこで同じ物質でも量が倍になれば、熱容量も倍になります。比熱はある物質1g (1mol, 1cc)を、1℃温度をあげるのに必要な熱量を言います。そこで、比熱に量をかけたものが熱容量になります。
気体の比熱については分子運動論なども含め様々な推算法が開発されていますが、液体の比熱に関しては、推算法は多くはありません。また、この比熱に関しては、臨界定数などから物性値を求める対応状態原理法の例は不勉強ながら知りません。
まず、数種類の化合物のモル比熱を温度に対してプロットすると図-11-31のようになります
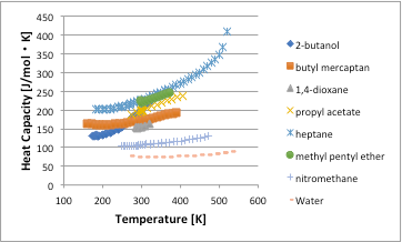
図11-31. 温度に対する比熱の関係
比熱は他の物性値と比べると,とても判りにくい物性値です。水やニトロメタンなどでは値が小さく,ヘプタンなどでは値が大きくなります。2-ブタノールはある温度から急激に比熱が高くなります。一見すると極性化合物で比熱が低く,非極性化合物で比熱が高くなるようにも見えます。極性化合物は強い分子間力を持つので温度はあげにくい化合物ですので比熱が低いのは納得しにくいです。
全ての液体は,温度が上昇するにつれ,1℃温度をあげるのに必要なエネルギーが高くなります。これらを合理的に説明するにはどうしたらいいでしょうか?
実は,これは単位系の問題です。化学系では蒸発潜熱など熱物性値をmolで考える事が多いです。化合物の違いはmol単位で
考えた方が理解しやすい面は確かにあります。しかし,工学系では,g, Kg, cm3, m3などの単位をよく使います。熱容量の温度依存性を単位系[J/g・K]に変えてプロットすると図11-32のようなります。
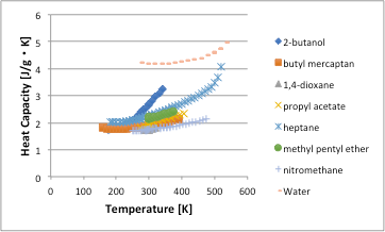
図11-32. 温度に対する比熱 [J/g・K]の関係
水などが大きな比熱を持ち,温めにくい性質である事がわかります。これは,水の1mol(18g)とヘプタンの1mol(100g)は大きく違うので,1℃温度を上げるのに必要な熱量は5倍以上違うのでmolで見ていてはわからないかもしれません。それでは,何故,温度が高くなると比熱が大きくなるのでしょうか?
この比熱の単位系を[J/MVol@Tref・K]に変更して見ましょう。MVol@Trefというのは,温度Trefの時の分子体積を言います。この値の算出は簡単ではありません。今回はHSPiPというソフトウエアーでの計算値を使いました。
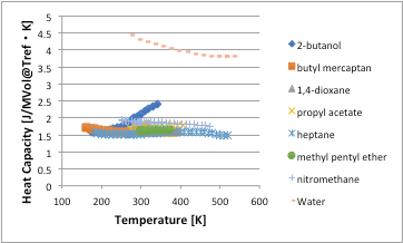
図11-33. 温度に対する比熱 [J/MVol・K]の関係
すると水,アルコールを除くと比熱の温度依存性は,ほとんどなくなる事がわかります。つまり,温度が高くなると比熱が大きくなるのは,体積が膨張するためであると言えます。体積当たりの比熱は水・アルコール以外は約1.6となり,温度に寄らずにほぼ一定になります。
液体の比熱の推算式の多くは、原子団に係数を割り振って、25℃の値を推算します。温度を他の値にした時の換算式は、不勉強ながら知りません。そこで、25℃で求まった値から分子体積で補正して任意の温度での比熱が求まるこの式は有用であると言えるでしょう。
水は分子体積が非常に小さな液体です。ですが水素結合の3次元的なネットワークを作り、クラスター化しています。ですから、単純な水の分子体積(非常に小さい)あたりの比熱でプロットすると他の液体よりは大きな値になります。水の比熱が、温度が高くなると小さくなる理由は難しいです。分子体積は一般に温度が高くなると大きくなります。他の液体では温度が高くなるにつれ、比熱も大きくなりますが、分子体積も大きくなるので、温度に依存しなくなりました。ところが水の場合、比熱も大きくなりますが、それ以上に分子体積も大きくなることを示しています。それは、クラスターサイズは温度の上昇とともに小さくなる事と矛盾します。水やアルコールなどのこうした不思議な挙動は今のところ私には説明がつかない事で、今後の解析が待たれる現象の一つです。
気泡核が成長し蒸発潜熱を奪うのと同時に、壁面からは熱が供給されます。どのくらいの熱量が供給されるかは熱伝導率で決まります。ある単位時間、単位面積を流れる熱流速密度、J[W/m2]は、温度勾配ΔTに比例するというフーリエの法則があります。
その比例定数の事を熱伝導率(λ)と言います。
J=λ*ΔT = λ*(t1-t2)/L
温度差((t1-t2))が高く、厚み(L)が薄いほど熱量が多く移動します。
熱伝導率の単位は[W/m•K]になります。
熱伝導率は一般的に測定温度が高くなると小さくなる物性値です。(水に関しては全く合わないので除外してあります。)
2-Butanolや水(600mW/mK)などでは大きな熱伝導率を持つことから、水素結合が大きく関与していると考えられます。
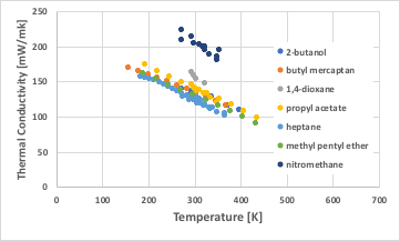
図11-34. 温度に対する熱伝導率の関係
この熱伝導率も、単位面積当たり単位厚み当たりの物性値なので、ある一定体積当たりに存在する分子の数に依存する物性値になると考えられます。そこで、(1-Tr)を分子の体積で割った値に対してプロットすると、図11-35に示す様に分子に寄らずほぼ一定の値になります。(水は残念な液体で、この処理をしても線には乗りません。)
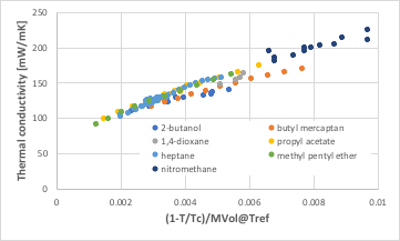
図11-35. (1-Tr)/MVol に対する熱伝導率の関係
代表的な対応状態原理推算法としては、Sato-Riedel法があります。
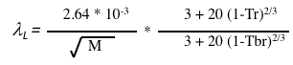
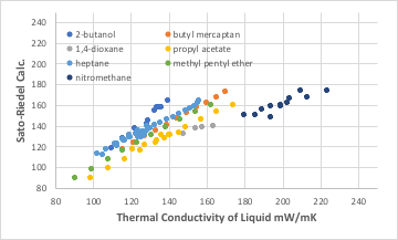
図11-36. Sato-Riedel式による熱伝導率の推算
余り精度の高い推算方法とは言えませんが、分子量と沸点、臨界温度だけから推算値が得られるので大雑把な値を得るには適しています。
筆者が開発した対応状態原理法による熱伝導率の推算式は以下の式で計算します。
Thc Liq.=232.14+0.652*(T/Tb)^-0.589* MW^-0.198* Tb^-1.096* Tc^0.227* Pc^2.199*Vc^1.182* Density^-0.392 -18.545* (T/Tb)^0.179* MW^1.159* Tb^-2.152* Tc^ 1.509* Pc^ 0.588* Vc^-0.1703* Density^-0.966
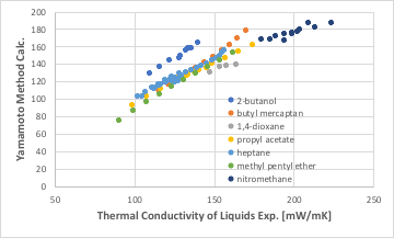
図11-37. 新規熱伝導率推算式
正則溶液では高い精度を持ちますが、水素結合性の溶媒では20%程度高い予測値になってしまいます。
気泡核の離脱
気泡がある大きさに達すると、壁面から離脱を始めます。離脱を決める物性値は浮力(密度差)、粘度、表面張力です。一旦気泡が離脱すると、周辺から液体が入り込んできます。その際に液体は激しく攪拌されるので、非常に大きな熱伝達率を持ちます。
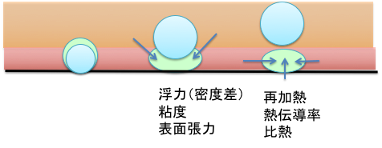
図11-38. 気泡核の離脱
本来は、レイノルズ数(乱流、層流を示す無次元数)で整理するべきでしょうが、ここでは、粘度と密度を説明することにします。
粘度は図11-39に示す様に、温度が高くなるにつれて急に小さくなる物性値です。縦軸はlogを取っていることに注意してください。
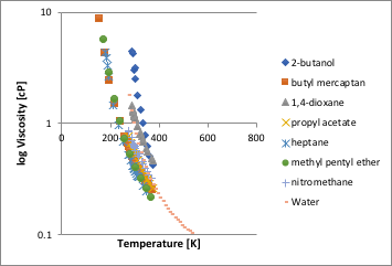
図11-39. 温度に対する粘度の関係
正則溶液では、ほぼ粘度―温度曲線は一致します。アルコールや1,4-ジオキサンは正則溶液よりも高い粘度を持ちます。非常に特異的なのが水で、温度が高い領域では正則溶液の曲線に近いのですが、温度が低くなってくるとアルコールの曲線に近づいて行きます。これは水の3次元水素結合が70℃付近で壊れていくことに相当していると考えられます。粘度の推算は非常に難しい推算とされます。ただ、粘度の温度依存性曲線は余り大きくは変わらないことから、粘度の実測値1点と感温性は正則溶液のものを並行移動して使う事も多い様です。
対応状態原理を用いた粘度の推算法にはLetsou-Stiel法があります。
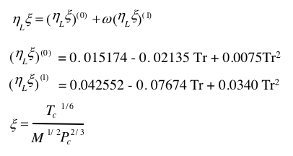
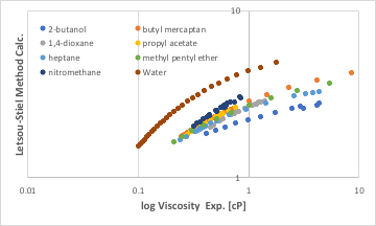
図11-40. Letsou-Stiel法による粘度の推算
図11-40から明らかな様にオーダーすら合わないので使い物になりません。
筆者が開発した対応状態原理法による粘度の推算式は以下の式で計算します。
log Viscosity=-1.884+0.544*(T/Tb)^-1.800* MW^0.523* Tb^2.235* Tc^-2.308* Pc^0.848* Vc^-0.332* Density^-0.651 +1.952*(T/Tb)^0.352* MW^-0.518* Tb^0.519*Tc^-0.782*Pc^-0.257* Vc^0.605* Density^1.194
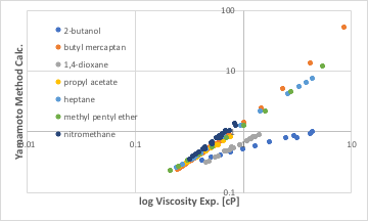
図11-41. 新規粘度推算式
水素結合の補正がないため、正則溶液でしか使えない式ですが、高い精度を持ちます。
密度は温度が高くなると値が小さくなる物性値です。
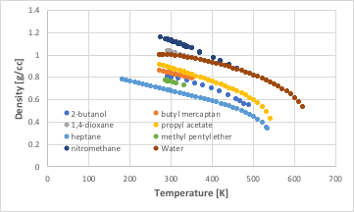
図11-42. 温度に対する密度の関係
温度が臨界温度に達した時に臨界密度に達します。
対応状態原理法の密度推算式にはYen-Woods法があります。

ρs:Density、ρc:Critical Density
Tr: TRef/Critical Temperature
Zc: Compressibility Factor
圧縮因子(Zc)の値によって係数を入れ替えますが、それなりに高い精度で密度の温度依存性を計算する事ができます。
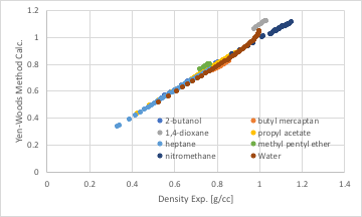
図11-43. Yen-Woods式による密度の推算
ただし、臨界温度、臨界圧力、臨界体積の値が皆揃っている必要があります。
以上見てきた様に、気泡の挙動を記述するのに必要な熱力学的な物性値の多くは、臨界点を基準として考えると明瞭に理解できる事がわかります。困り者は水素結合性の化合物です。粘度の項でふれた様に水の3次元水素結合は70℃付近で壊れます。アルコールの水素結合とどうも挙動が異なります。臨界点では水素結合も含めて分子間力と熱エネルギーが釣り合っているのでしょうが、臨界点から離れるにつれて、水素結合の効果が現れ、物性値の予測を難しくしていると考えられます。対応状態原理とは異なるアプローチですが,ハンセンの溶解度パラメータ(HSP)の水素結合項などを導入するというのは一つの解決方法だと思います。
第10章,11章は例えば低温の地熱発電用途向けの,フロン代替化合物や自然媒体を蒸発させることを想定しています。本来はそうした化合物に加え,水やアルコールなど水素結合性の化合物まで統一的に解釈できればよかったのですが,力量が及びませんでした。時間を見つけて改定していこうと思います。
Gibbsの相律(忘備録)
状態量は示量性状態量と示強性状態量に分類できるといいます。示量性状態量とは,文字通り量を示す変数で,加成性があります。代表的な例が質量や体積です。AgとBgを混ぜればトータルは(A+B)gになります。示強性状態量は強さを示す変数で,加成性がありません。温度や圧力が代表的な例です。10℃と30℃を足し合わせても意味を持たないので,相加性はありません。この二つの状態量の中には互いに掛け合わせると示量性状態量になるものがあります。そのような関係を互いに共役な関係と呼びます。例えば体積と圧力を掛け合わせるとエネルギーの次元を持った示量性状態量になります。密度は示強性状態量となります。こうした示強性状態量の自由度を規定するのがギブスの相律という式です。
F=C-P+2
Fは示強性状態量の自由度,Cは成分の数,Pは相の数,そして定数の2は温度と圧力の2つの示強性状態量から来ています。1成分3相は自由度ゼロ。これは3重点を示しています。1成分2相(気相と液相が共存)は自由度1。そこで,温度が決まれば圧力が決まります。1成分1相(液相のみ,気相のみ)は自由度2。温度と圧力が決まらないと状態が記述できない事がわかります。
雑記
化学工学はITに見捨てられた分野とかいう自虐的な言い方がありました。流れの解析用のソフトなどはずいぶん進歩しましたが,昔からある有限要素法が,高速化,大容量化したのでメッシュが細かくなっただけなので,ITの進歩という感じはあまりしません。何故ITに見捨てられたのかと言えば上記のような難しい問題が内在していたからです。最新のAIならどうなるでしょうか? 自動的にモル・ベースを重量ベースに変えて式を組み立てて行くくらいのAIが出現するのはそう遠く無い事でしょう。Antoine BをKJ/Kgベースに変えて,空間の圧力ではなく,空間中の重量を予測する3パラメータを決定する式ぐらい簡単に作るかもしれません。筆者は、かれこれ20年間ニューラルネットワークを使った物性研究をやってきて得られた結論は、精度が高い,中がブラックボックスのニューラルネットワークより、中身が見える精度の低いニューラルネットワークの方が大事というものでした。その発想で定めたAntoine定数が蒸発現象の解釈に,たまたま役に立ったということです。これは既に過去の話で,現在は,次の時代に向けてAIをどう教育したら自律的に化学-化学工学-式の組み立て-逆設計をこなしていかれるのかに焦点は移っていています。そうした時代に若手研究者の卵が何を学び社会へ巣立っていくべきか,学生と考える機会を提供いただいている横浜国大には感謝しております。
