2025.01.19
情報化学+教育 > YMB Pro for MI >
YMB25Pro4MIのSphere探索プログラム
注意:HSPiPに搭載の機能ではありません
Sphere法の基本
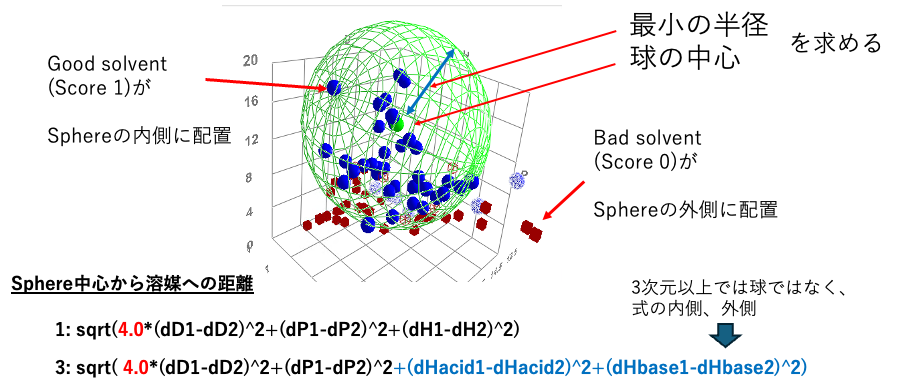
Sphere法というのはHansen先生が作られた、溶質のハンセンの溶解度パラメータ(HSP)を探索するアルゴリズムだ
HSPが既知の溶媒を(dD, dP, dHをベクトルとみなして)3次元空間にプロットする。良溶媒を青く塗る。貧溶媒を赤く塗る。良溶媒と貧溶媒の境界は研究者が定めて良い。この溶媒がプロットされた空間をハンセン空間と呼ぶ。すると、青い良溶媒はハンセン空間上で集まって球(Sphere)を作っていることにハンセン先生が気がついた。この緑の大きなメッシュの球をハンセンの溶解球と呼ぶ。そして溶解球の半径を相互作用半径と呼ぶ。溶解球の中心(塗りつぶしの小さな緑の球)を溶質のHSPと定める。
HSPiPに搭載されているSphere法は、溶媒とScore(0:貧溶媒、1:良溶媒)から溶解球の中心と半径を求めるプログラムだ。溶解性が未知の溶媒を考えたときに、そのベクトルが溶解球の中に入った時には、研究者が定義した程度に”良く”溶質を溶かすことになる。
HSPiPのver.3.1からはdH(水素結合項)をAcid, Baseに分割する方法が提供されている。4次元になるので球では表現できなくなる。式の内側、外側で判定する。
Sphere法の拡張
私は、HSP50周年記念講演会でキーノート・スピーチを2つ行い、HSPの拡張を提案した。
1つ目は、分散項(dD)の分割だ。
2つ目は、水素結合項の分割タイプの拡張だ。
この2つの拡張を行うと33種類の新しいHSP距離の式が出てくる。
33種類のうち、どの式が最も良い式なのか聞かれる。それを答えるのは不可能だ。
溶解・分散現象を深く理解するためにいろいろな式を詳細に評価するのが大事だと言っているだけだ。
一般化できた式は将来HSPiPに搭載されるかもしれない。HSPiPのユーザーは搭載されるまで待って頂きたい。
分散項(dD)の分割
分散項の前のファクーター4
HSPの距離の式で分散項の差分の前には4.0というファクターがついている。
sqrt(4.0*(dD1-dD2)2+(dP1-dP2)2+(dH1-dH2)2)
3次元ベクトルの距離であれば4.0はいらない。
まず、このファクター4.0を考える。
希ガスとフッ素化合物
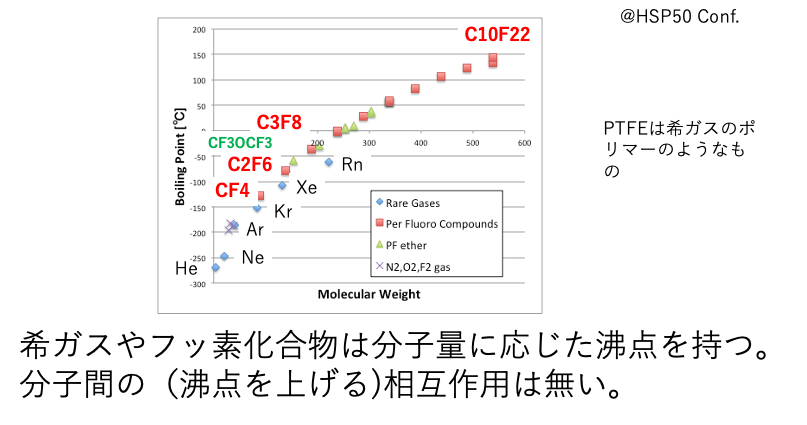
HSP50で講演した内容だ。希ガスの分子量と沸点をプロットする。データはキレイに曲線の上に乗る。さらにパーフルオロのアルカンやエーテルを加えても曲線に乗る。これらの元素・化合物の沸点は分子量だけで決まっている。弱いファンデルワールス(vdw)力しか持たない化合物と考えて良い。
dPとdHを持たない化合物
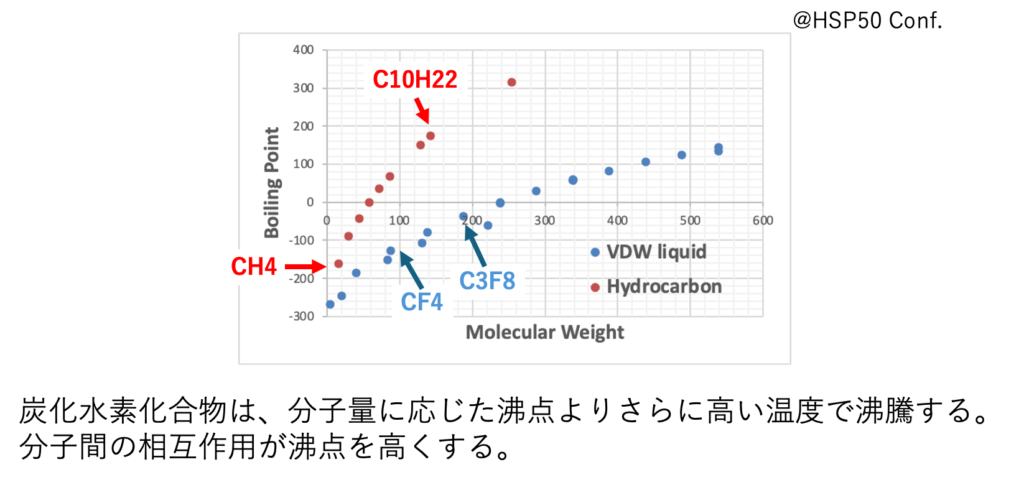
HSPは元来、分極項(dP)と水素結合項(HC)を持たない炭化水素(HC)をベースに考えてきた。しかし、VDW液体と比べるとHCの沸点はとても高い。これは動的自由度などからも考えうる。
動的自由度
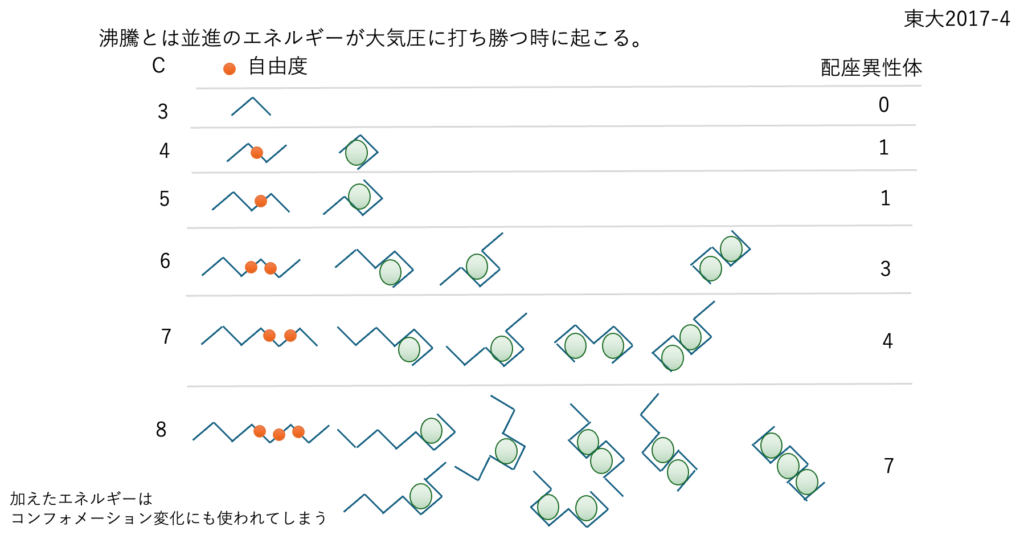
沸騰は並進のエネルギーが大気圧に打ち勝つ時に起こる。しかし配座異性体の多い化合物は加えたエネルギーが並進だけに使われないので沸点が高くなる。

同じ炭素数でもt-ブチルのような回転障壁の高い基を持つ化合物は直鎖状の炭化水素と比べ20度から30度沸点が低くなる。しかし、これだけではVDW液体の沸点との差は理解できない。蒸発とは何かは、まだまだ考え続けなければならない。
軸の変換
沸点と蒸発潜熱には相関がある。Troutonの法則として知られている。そこで縦軸を蒸発潜熱に変える。分子量のルートを取ったものを横軸にする。
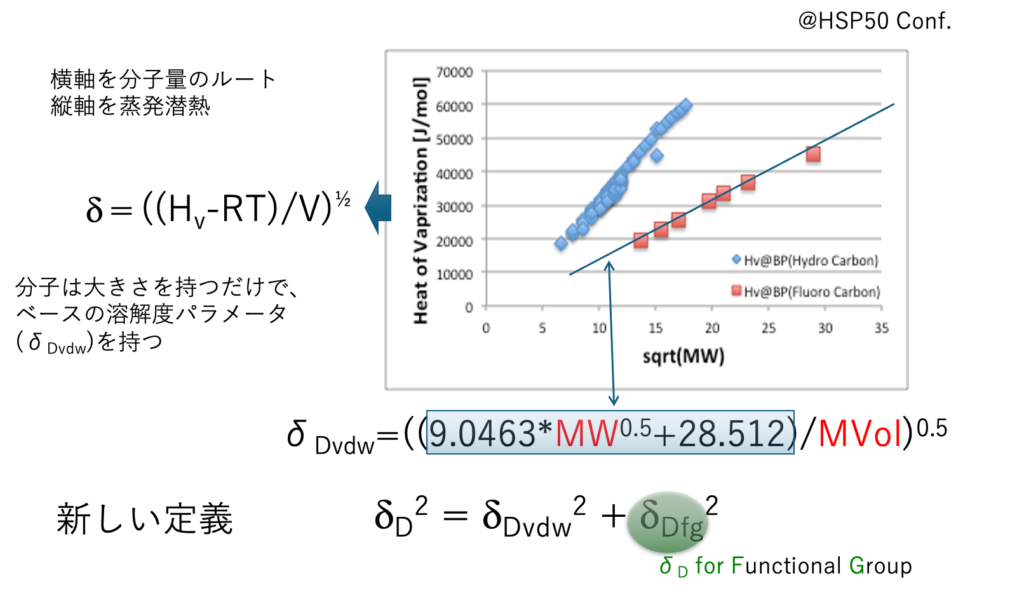
VDW液体は赤い四角になり、直線近似できる。
Hv=9.0463*MW0.5+28.512
この式の意味することは、任意の化合物の分子量がわかれば、それを蒸発潜熱に変えることができるという事だ。
この蒸発潜熱を分子体積で割ってルートを取る。これは溶解度パラメータの定義だ。
dDvdw = ((Hv-RT)/V)½
分子は大きさ(分子量)を持つだけで、ベースとなる溶解度パラメータdDvdwを持つ。炭化水素はベースとなる分子量に対応する蒸発潜熱に加え、より多くの熱が必要になる。その分は官能基ごとの相互作用としてdDfg (Functional Group)と定義する。
このようにHSPの分散項は2つの成分に分解できる。
dD2 = dDvdw2 + dDfg2
dD、分子量、分子体積がわかっているので、任意の化合物のdDfgは計算することができる。
新しいHSP 距離
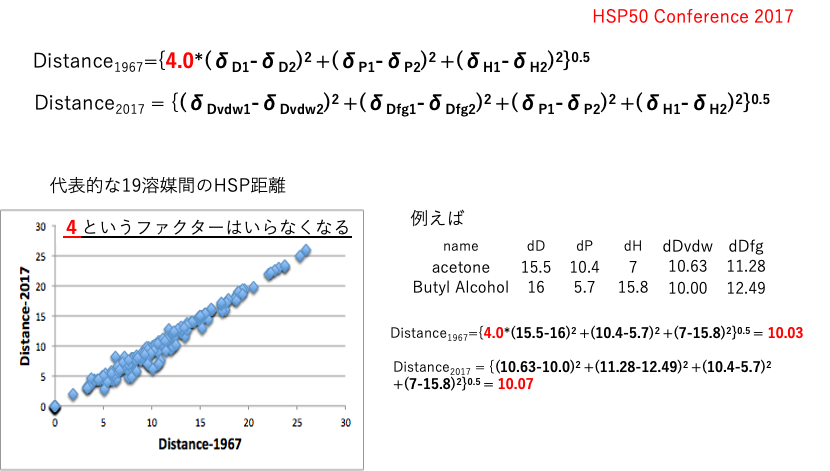
HSP50記念講演会で、新しい距離の式Distance2017を提案した。代表的な19溶媒の相互HSP距離を計算してみた。
元々の1967年の距離の式では分散項の前に4.0という説明困難なファクターが入っていた。しかし2017年のdDを分割した式では、4というファクターが無くても、ほとんどのケースで距離が変わらないという結果になっている。
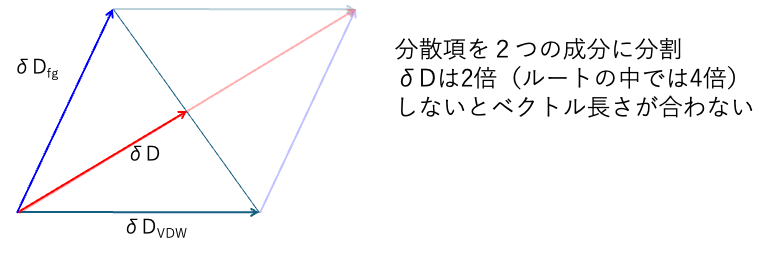
合成ベクトルの考え方からすれば、δDは2倍(ルートの中では4倍)しないと合わなくなるのだろう。
ポリマーの溶解性(HSPiPの例題)
HSPiPには使い方を理解するための例題が付属している。PolymerA-ALは市販のポリマーを88種類の溶媒を用いて溶解性試験を行なったデータだ。これをHSPiPで計算した1967年の距離の式と2017年のものとで比較した。
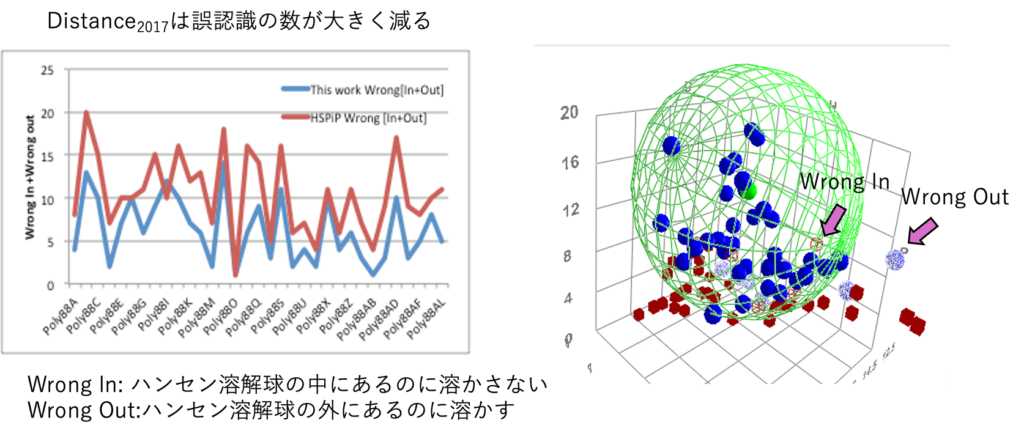
評価はWrong In/Outの総数で行った。Wrong Inというのはハンセン溶解球の中にあるのに溶かさない溶媒をいう。Wrong Outというのはハンセン溶解球の外にあるのに溶かす溶媒をいう。Distance2017は、ほぼ全てのケースで誤認識が減っている。HSPiPで3次元で見ている時には誤認識の意味は明確だ。最初に良溶媒は青くマークしてある。貧溶媒は赤だ。Sphere法が緑の大きなメッシュの球とその中心(ポリマーのHSP)を探索する。青い溶媒(良溶媒)なのに溶かさなかった場合、色が青抜きになる。赤い溶媒(貧溶媒なのに)緑のメッシュ球の中に入った場合はWrong Inになり赤いメッシュ四角になる。2017年の距離の式では4次元になるので、プロットはできない。式の内側・外側の評価になる。
どうして分散項の分割が良好な結果になるのか考察してみよう。
分散項の比較
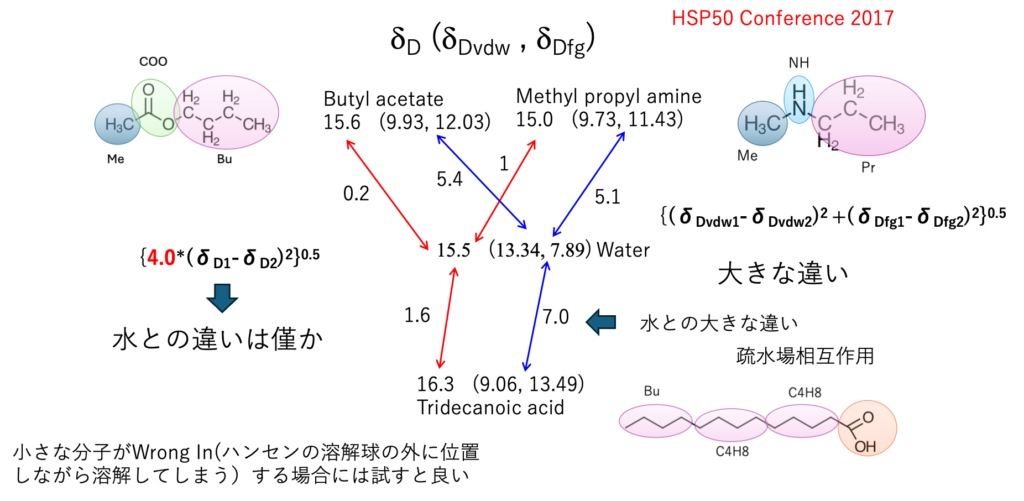
試しにエステル、アミン、カルボン酸と水との距離を分散項だけ検討する。
1967年の距離の式で {4.0*(δD1-δD2)2}0.5 を使って水との距離を計算するとエステル(0.2)、アミン(1.0)、カルボン酸(1.6)とあまり大きくは変わらない。
2017年の距離の式で{(δDvdw1-δDvdw2)2 +(δDfg1-δDfg2)2}0.5 を使って計算するとエステル(5.4)、アミン(5.1)、カルボン酸(7.0)と大きく異なる。
長鎖カルボン酸の塩は界面活性剤として使われる。
界面活性剤を水に溶かすと何故ミセルを作るのだろうか。
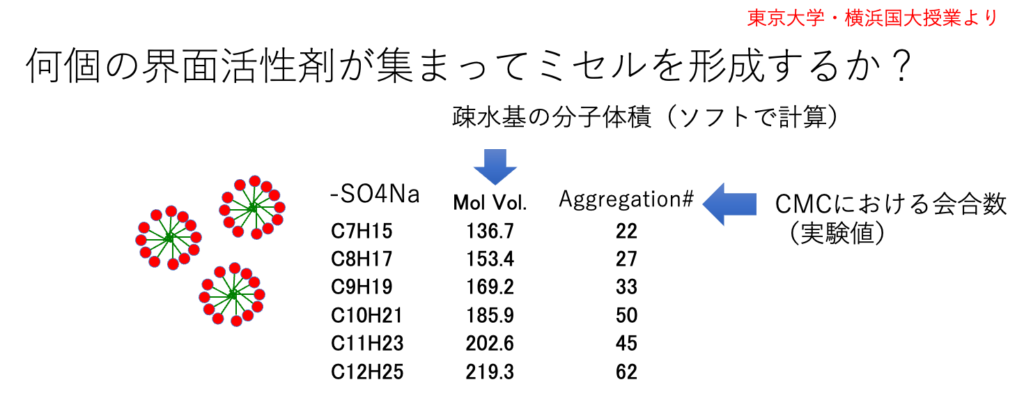
カルボン酸の塩の部分は水溶性が高い。その部分が水に溶けるのは理解できる。しかし何故、直鎖の部分は集まるのだろうか? 疏水場相互作用とか簡単に流されている。
水との溶解度パラメータが大きく異なるので、直鎖の部分は直鎖の部分に溶解するという言い方をしたいのだが、1967年の距離の式 {4.0*(δD1-δD2)2}0.5 では、エステル(0.2)、アミン(1.0)、カルボン酸(1.6)とあまり変わらない。これではHSPで界面活性剤を説明できないことになる。
それに対して2017年の式 {(δDvdw1-δDvdw2)2 +(δDfg1-δDfg2)2}0.5 では長鎖のカルボン酸の水とのHSP距離が長くなる。そこで長鎖の部分は水の中にいるより、集まった方が安定になる。これがHSP的にミセルが形成される理由になる。
小さな分子がWrong In(ハンセンの溶解球の外に位置しながら溶解してしまう)する場合にはこの分割を試すと良い。
dDvdwは溶解性に必要か?
2017年の距離の式が有効であるのは分かったが、dDvdwは本質的に重要なのであろうか? それを調べるために、dDvdwのない式で先ほどのポリマーの溶解性を評価した。
Distancefg = {(δDfg1-δDfg2)2 +(δP1-δP2)2 +(δH1-δH2)2}0.5
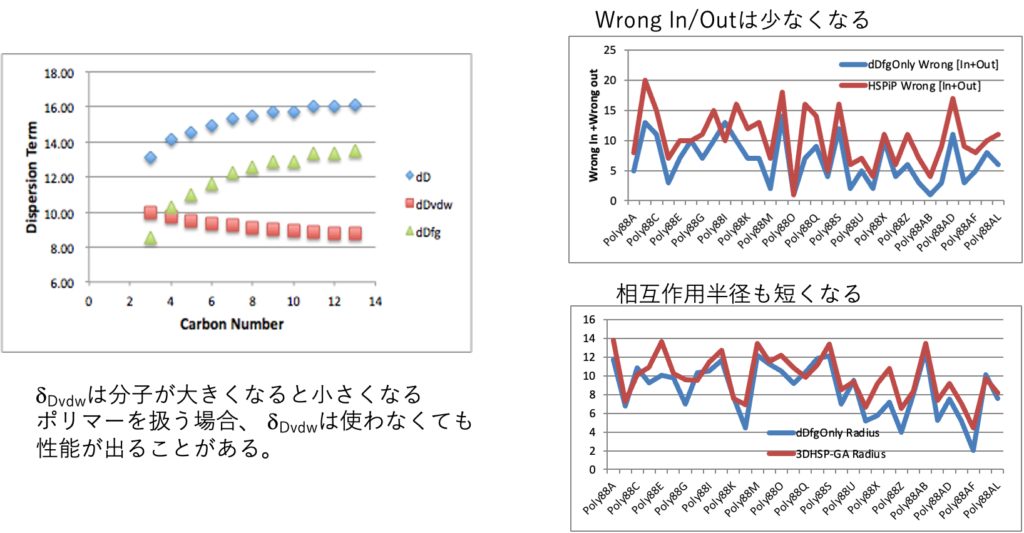
dDvdwを使わなくても、Wrong In/Outの数は十分少なくなった。したがってケースによってはdDvdwを使わなくても性能は出る。
dDvdwは分子が大きくなると、小さくなっていく。この性質は、ポリマーのように分子が大きくなっていくとdDvdwは意味を持たなくなっていく。そこで大きな分子を扱う場合にはDistancefg の距離が有効なことが期待される。
シリコーンオイルとフッ素オイル
どちらも疎水性のオイルで、水を弾くことから、衣料品のコーティングなどに使われている。どちらも疎水性であるがお互いには混じらない。何故だろうか?
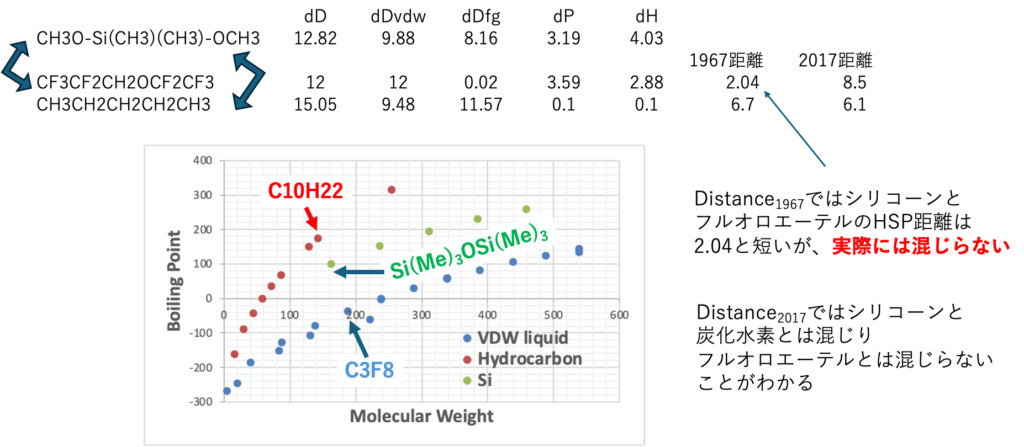
1967年の距離を使うと、シリコーンオイルとフッ素オイルは距離が2.04と短い。それなのにこの2つが混じらない事はHSPでは説明できない。
シリコーンはメチル基を多く持つために、沸点(蒸発潜熱)は低下する。また分子量に対して分子体積は大きい(密度が低い。Si-O結合が長く分子が大きい)。そこでSP=sqrt(Hv/MVol)で計算するとSP値は小さくなる。フルオロエーテルはdDfgをほとんど持たない。原子団との相互作用を持てない。そこで1967年の式と2017年の式では解釈が全く異なる。
フッ素化合物の表面は、フッ素の大きい電気陰性度のためマイナスにチャージしているとか解釈されるが、それは間違いだ。表面がマイナスにチャージされているなら、PTFEのポリマーとポリエチレン(表面が水素で覆われている。水素の電子は結合に使われていてポリマーの表面はプラスにチャージされている)はものすごく良く接着するはずだ。そんなことはない。
先にPTFEは希ガスのポリマーと書いた。
パーフルオロの分子表面はゼロと考えないと合わない。
プラスが来ても、マイナスが来ても、とっかかりが無い表面になる。
閑話休題
この違いはdDを2種類に分割しないと理解できない。
ポリジメチルシリコーンゴムの膨潤度
PDMSのゴムはパッキンなどに利用されている。
スカスカ・ポリマーなので気体バリアー性は高くないが、水系用のパッキンとして締め付けて使う。
どんな溶媒でどのくらい膨潤するかのデータがある。
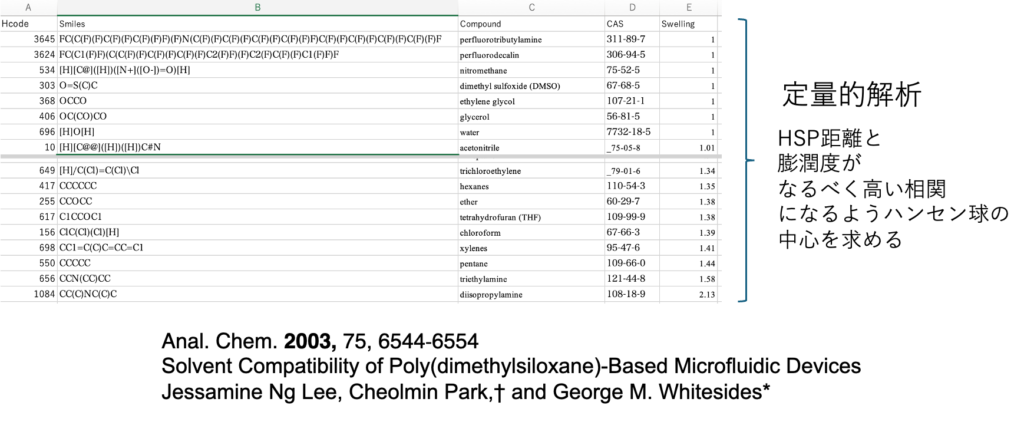
この場合には、良溶媒(1), 貧溶媒(0)という定性的解析では無く、定量的な解析になる。HSPiPでもData Pointsとして解析することができる。
定量的解析
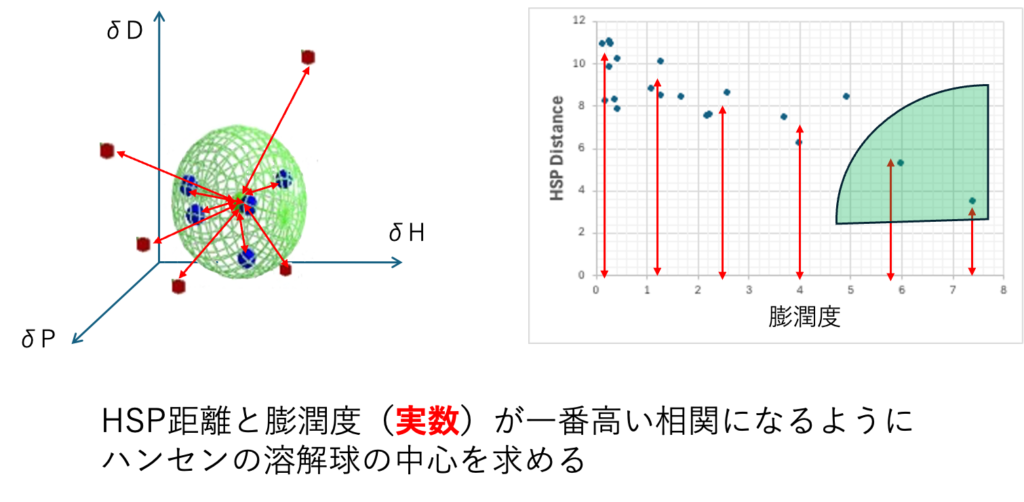
定量的解析ではHSP距離と何らかの評価値(実数)が一番高い相関になるようにSphereの中心を求める。
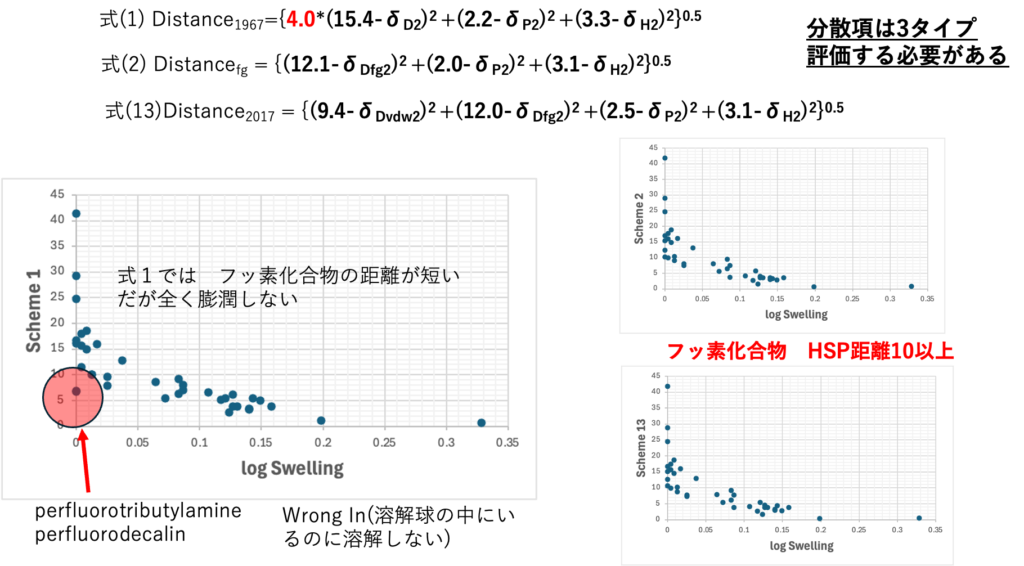
この時に1967年の距離の式を使うと、フッ素化合物で誤認識してしまう。
フッ素化合物はHSPはシリコンゴムと似たようなHSPを持つがシリコンゴムを膨潤させない。
分散項をdDvdwとdDfgに分割すると、シリコーンゴムとフッ素化合物の距離はとても長いので膨潤させないことが理解できる。
小さい分子が入ったら分割が有効。
フッ素化合物が入ったら分割が有効
ポリマーなどではdDfgのみでも良いかも
一概にどの式が良いかは言えない。
どの式が一番良いかを競うものではない。
溶解や分散を理解する上でタイプの違う式からどんな知見を導き出すかを競うものだ。
水素結合項の分割
酸・塩基性
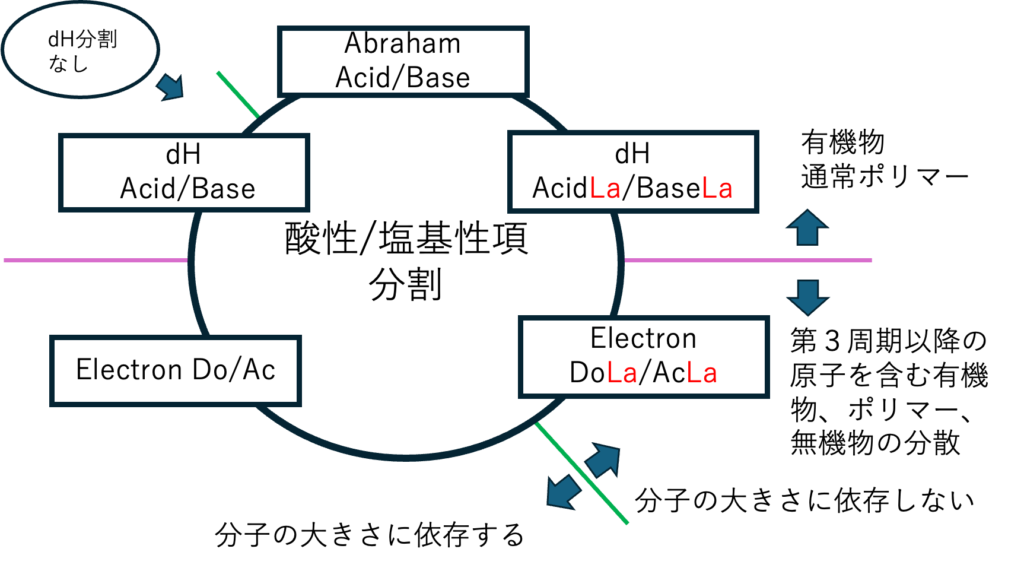
水素結合項はHSPiPのver.3.1(2010年)から酸・塩基への分割法が搭載された。ロンドン大学のAbraham先生を訪問して、様々な化合物のAbrahamの酸・塩基の定数を頂いた。これを参考にHSP用のdHacid,dHbase(HSPiPではdHdo, dHacと表記されている)を決定した。
この分割はほとんど使われていない。この分割を利用して、どんなHSP距離の式を作るかで、Abbott先生と私で意見の相違があった。先生は複雑な条件式をつけて分類しようとした。私は単純なEuclidタイプの分割で良いとした。
HSPiPに搭載するのは先生なので、ほっておいた。
最近見たら、結局は私の主張したEuclidタイプに変更したようだ。でも私の作ったGA法では使えないようになっていた。
こうした意見の相違はよくある。
2017年のHSP50周年講演会で、私は2つのキーノート・スピーチを行った。
dD項の分割についてはもう述べた。
もう一つは水素結合項の分割だ。そブレンステッド酸・塩基はAbrahamのもので導入済みだ。さらに、Lewisの酸塩基を導入した。GutmannのDN(Donor Number), AN(Acceptor Number)を分子のSmiles構造式から予測する式を開発した。
Y-MB pro搭載のED, EA予測式
全ての化合物をMO計算し、Electron Donor/Acceptor (ブレンステッドは酸・塩基、ルイスはドナー・アクセプターを使うようである。HSPiPではプロトン・ドナー/アクセプターとして使っている。混乱を避けるために、私はED/EAを使っている)をSmilesの構造式から予測するQSAR式を構築した。
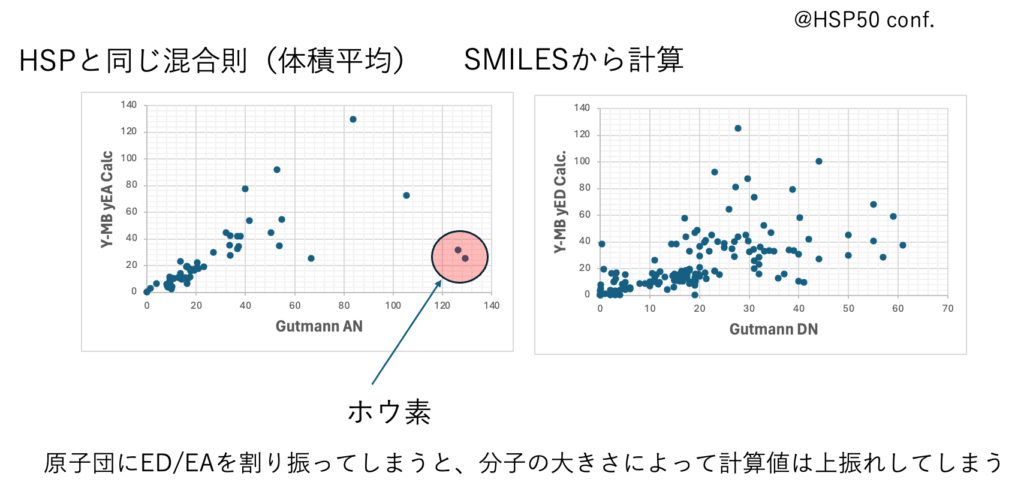
官能基を一つしか持たない化合物4000化合物から作成した式である。すると複数の官能基を持つ化合物のED/EAが幾つになるか、とても難しい問題になる。混合則がない。HSPiPに搭載されている化合物に拡張しようとすると複数の官能基を持つ化合物をどうするかはとても悩ましい。
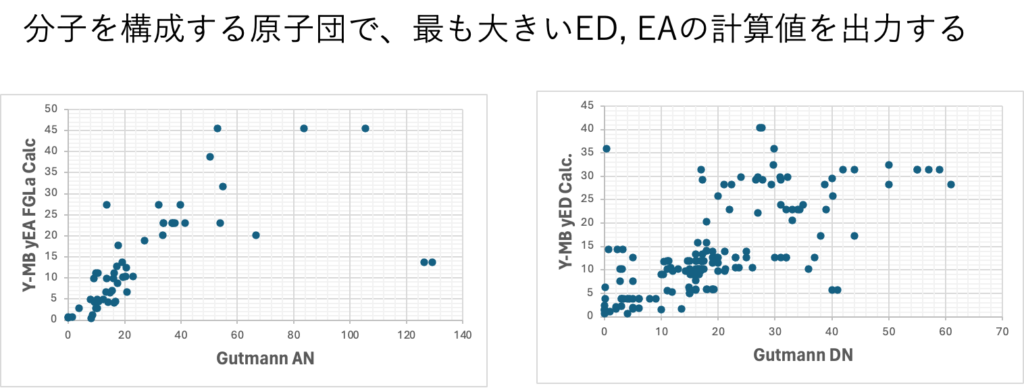
混合則をどうするかは後回しにして、とりあえず、分子中で一番大きいDN/ANを持つ官能基だけに注目する(yEDLagest, yEALargest)事も可能だ。yというのは山本の作ったED/EAのことだ。
2023年までは、yED/yEA, yEDLa/YEALaをQSAR/QSPR用の識別子として使っていた。その場合には、距離の式の面倒な取り扱いはいらない。結果オーライのデータ駆動型研究と言っていれば良い。
2024年からyED/yEA, yEDLa/YEALaをHSP距離の式に導入することを考え始めた。
きっかけは、2023年のドイツで行われたHSPのWorkshopだ。
Workshop HSP for Particles 2023.Dec
無機物の分散に関してQSARを適用するとED/EAが重要な項目として選択される。
これを距離の式に持ち込むことを考える。
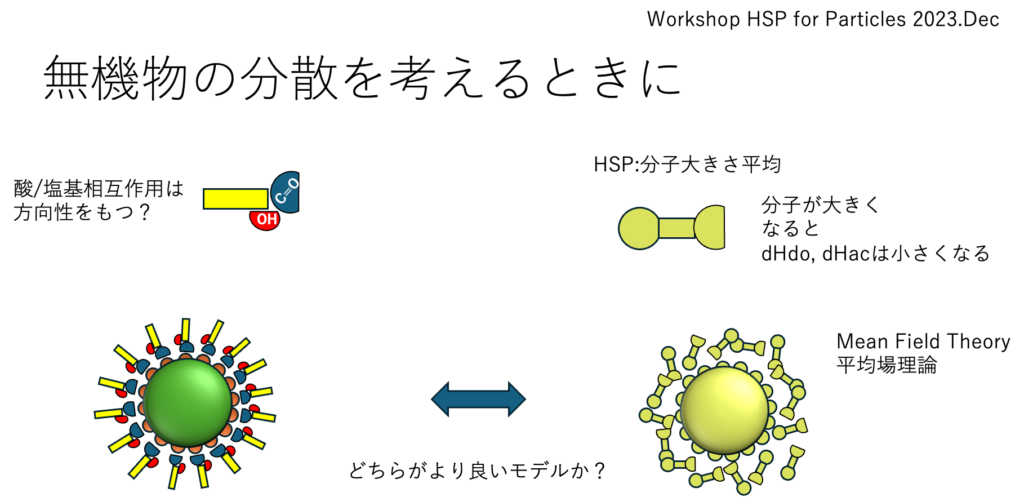
HSPは平均場理論になる
ドイツの講演で私が主張したのは、無機物の分散は平均場理論で説明できないということだ。分散性に方向性を持たせる。
HSP: 基本原理
ギリシャの自然哲学の時代は「愛はモノを惹きつけ、憎しみはモノを引き離す」と言われた。ニュートンの自然科学の時代「似たものは似たものを溶かす」になった。これは偽金貨作りの合金作りの話だ。Hansen先生はHSPが似たものはHSPが似たモノを溶かすという。
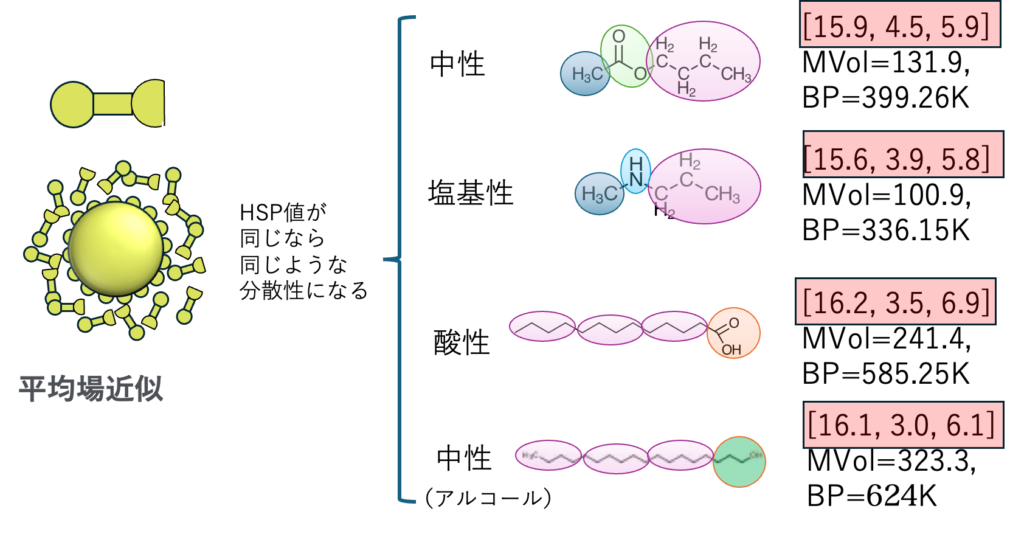
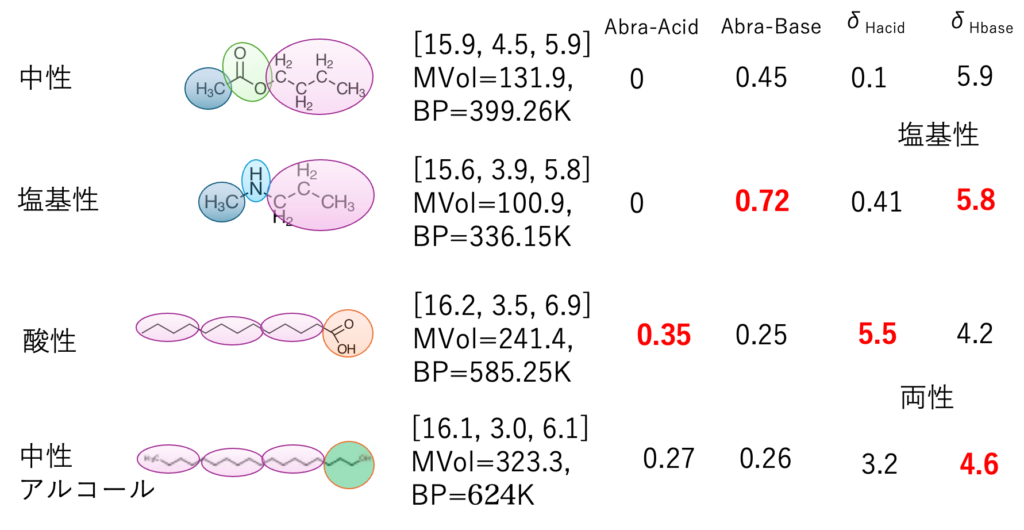
例えば、これらの4化合物はHSPがほぼ同じになる。酸/塩基/中性化合物のHSPがほぼ同じだからって、溶解性や分散性がどれも同じだとは誰も思わないだろう。
それなのに、この50年間、不思議とうまくいっていた。
うまくいくと、その技術を広い範囲に使ってみようと思う研究者がどうしても増えていく。
私はかなり早くからその限界に気づき、拡張を行なってきた。
それががやっと役に立ち始めた。
酸・塩基・両性
環境化学(Journal of Environmental Chemistry)Vol.30, pp.145-150, 2020
環境有機化学実験における溶媒の選択
遠藤 智司
は酸塩基のとても参考になる。ネットで拾えるので是非読んでみるといいだろう。
δHの酸、塩基性分割

まず、2010年には水素結合項を分割した。
基本となるAbraham先生のAcid/Baseは500化合物ぐらいの値を頂き、Smilesの構造式から値を予測する式を作成した。初期はAbraham先生のAcid/Baseを構造から推算して、dHを構造から予測して、それを分割していた。
推算の推算になるので、今では直接dHacid/dHbaseを予測するように変更した。
そこでdH2 = dHAcid2 +dHbase2は成立しなくなった。
HSP値では区別しにくいが、少し差がわかりかけてくる。
カルボン酸とアルコールの両性は、値だけから見ていると区別が難しい。
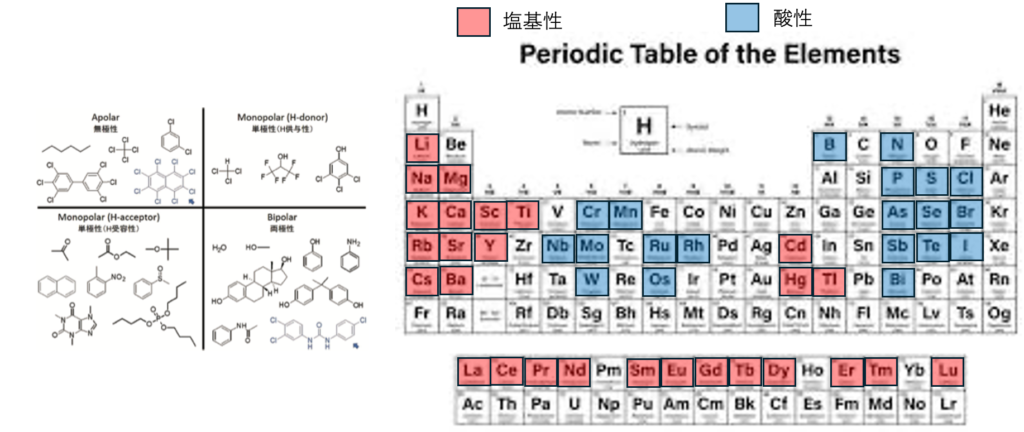
AbrahamのAcid, Base
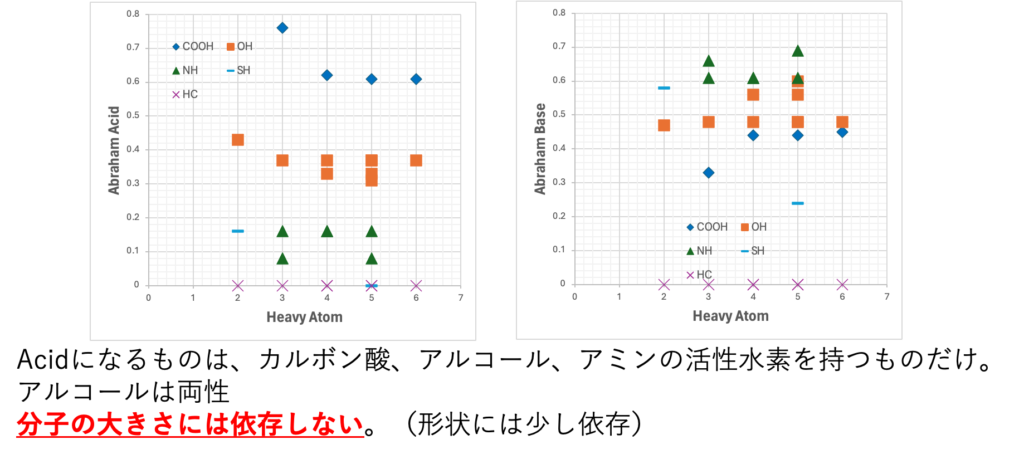
Abrahamの定義では、アミン、カルボン酸、アルコールの活性水素を持つものは両性になってしまう。アミンはdHacidは小さい。それ以外のヘテロアトム(O,N, S, P)を持つものは皆dHbaseになる。
δHacid, δHbaseの分子大きさ依存
溶解度パラメータの定義では
SP=sqrt((Hv-RT)/Vol)
と分子体積に依存してしまう。
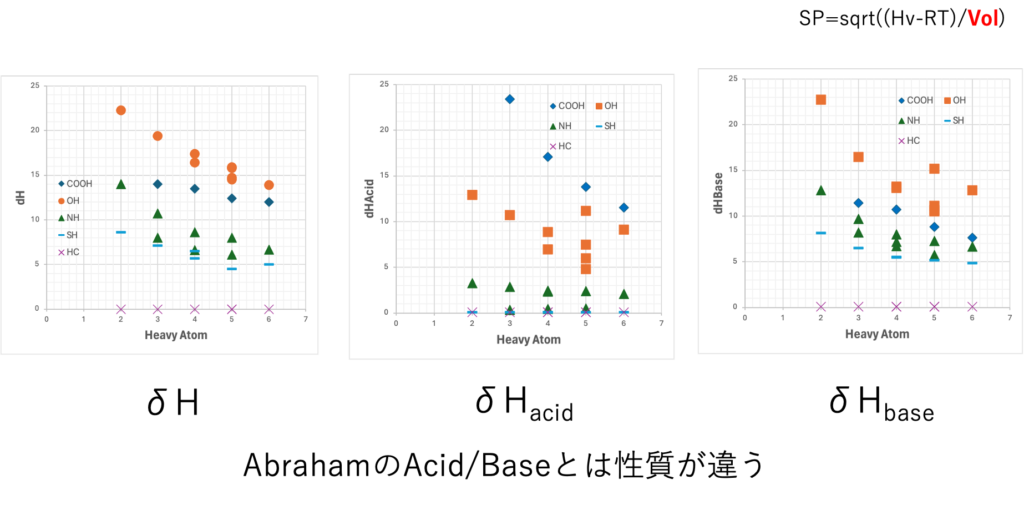
dH, dHacid, dHbaseは、分子が大きなるとどんどん小さくなる。この性質はAbrahamのAcid/Baseとは決定的に異なる。
分子の大きさに依存しない物性
カルボン酸の物性を考えてみよう。
沸点や屈折率、粘度、表面張力など様々な物性がある。その中で分子の大きさに依存しない物性はどんなものがあるだろうか。
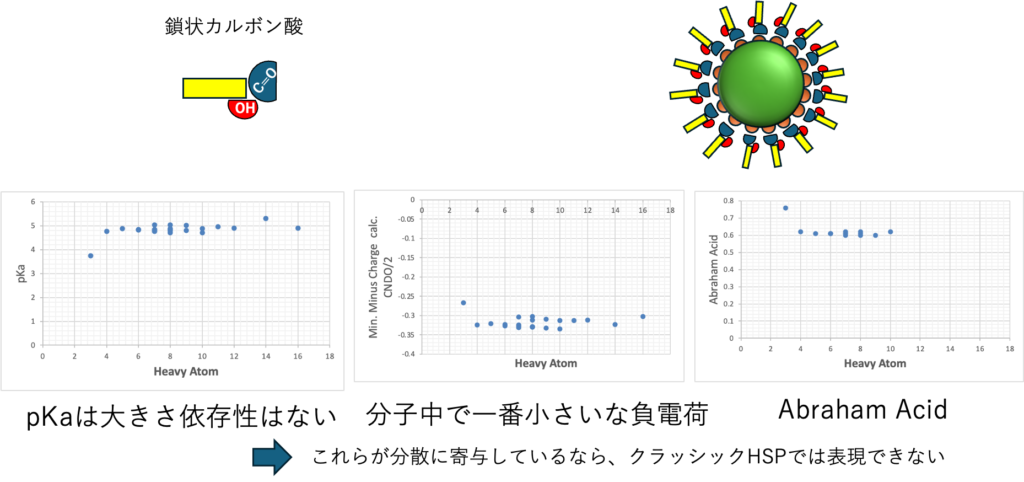
分子の一番小さい蟻酸だけは少し異なるが、上記の物性は炭素鎖数に依存しない。
例えば、MO計算から出てきた一番小さな負電荷が粒子表面の正電荷と相互作用して分散安定化に寄与している、ならカルボン酸の鎖長には依存しないだろう。
酸/塩基は平均場近似でないとするなら
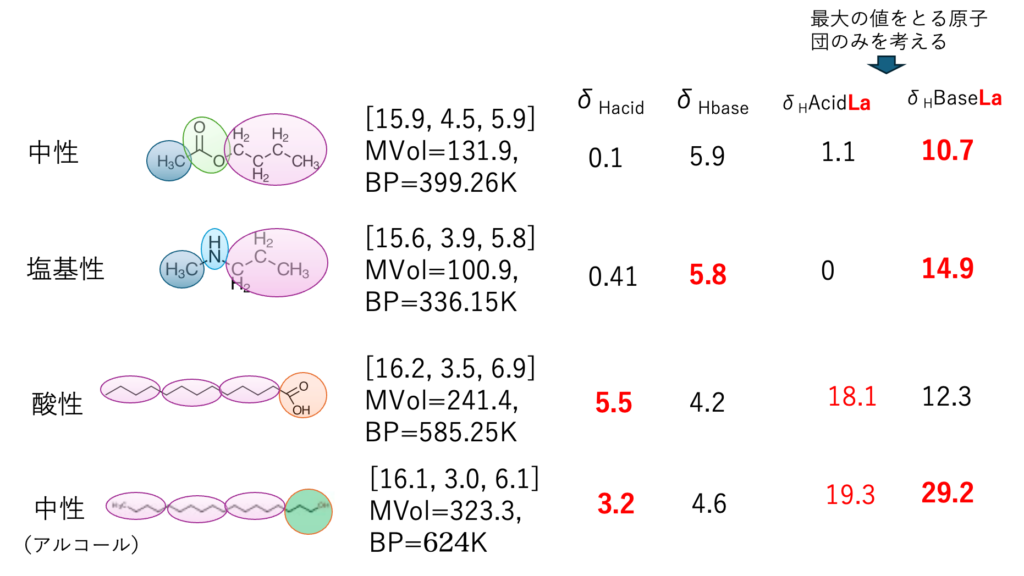
カルボン酸を1つだけ持つ化合物は、鎖長によらず分子中で一番大きなdHacid, dHbaseを持つ原子団はCOOHになる。dHacidLa, dHbaseLaは、複数の官能基を持つ化合物でも一番大きな値だけを考える。
ルイスの酸塩基
2016年にはGutmannのDN, ANを予測する式を作成した。
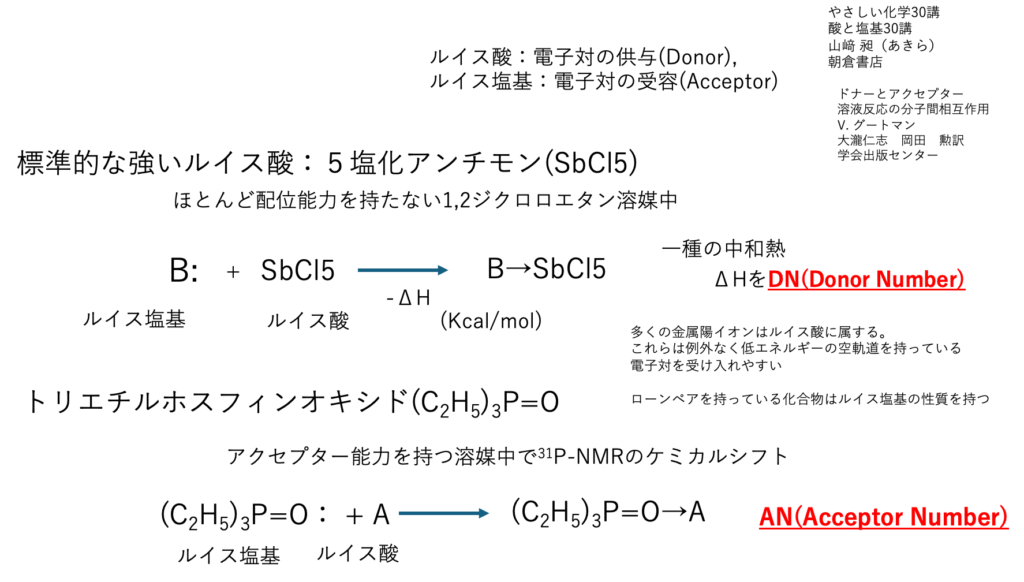
このルイスの酸塩基はローンペアの受授になるので、方向性が出てくる。
大事な点は、多くの金属イオンはルイス酸に属することだ。低エネルギーの空軌道がローンペアを受け入れる。周期律表で第3周期から空のd軌道を持つ。
これまでのHSPがうまく行っていたのは、主に水素からフッ素までの元素しか扱ってこなかったからだろう。
無機微粒子がフッ素より上の元素を使っている場合、ルイス酸塩基の考え方が重要になってくる。
例えばSbが表面に分布している微粒子を考える。
ルイス塩基性は分子サイズに依存するか?
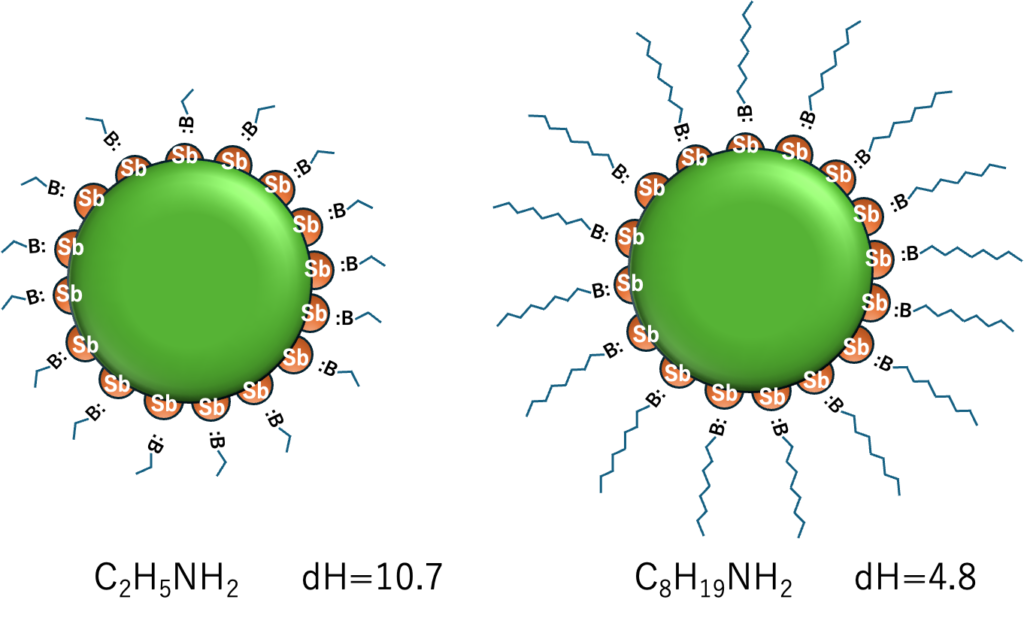
先にも書いたように、分子が大きくなるにつれdHは小さくなる。NH2のローンペアをSbに供与する際に、後ろの鎖の長さは供与性に影響を与えるだろうか?
複数のルイス塩基点があった場合の混合則
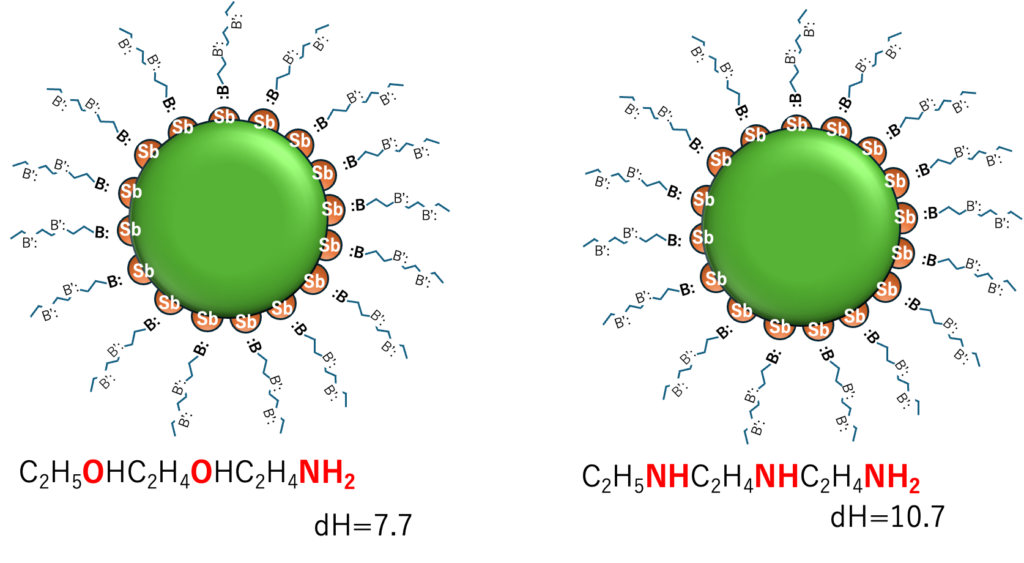
複数のルイス塩基点があったときの混合則はどうなるのだろうか?
残念ながら答えを持ち合わせていない。
やってみるしかない。
ルイスの酸/塩基
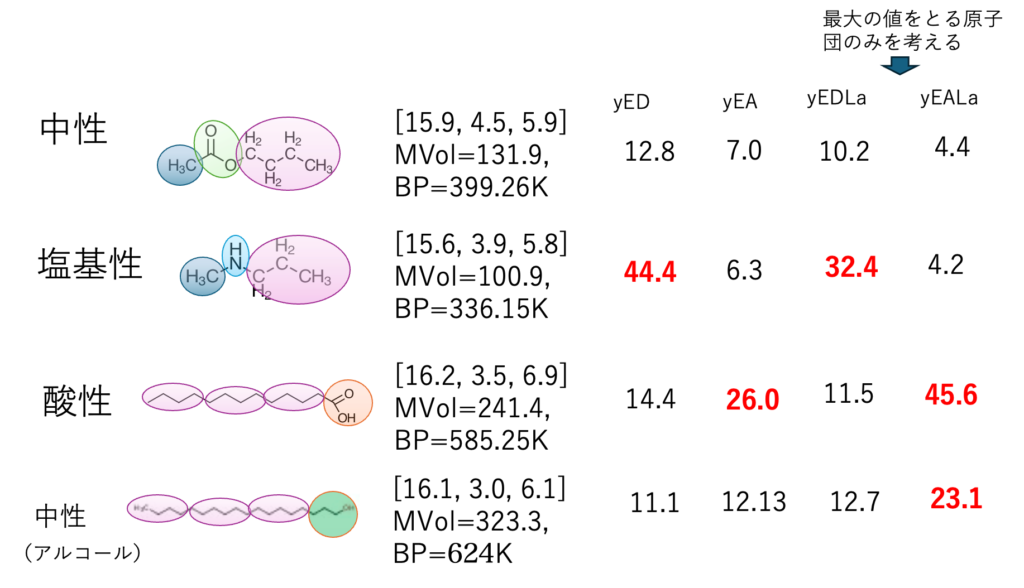
Acid/Baseの時と同じように、yED/yEAとyEDLa/yEALaを使うことにする。
酸塩基分割
交換作用による分散
弱酸・弱塩基の塩に強酸を入れれば交換反応が起こる。それが溶解や分散にどう影響するかは、ケースバイケースになる。
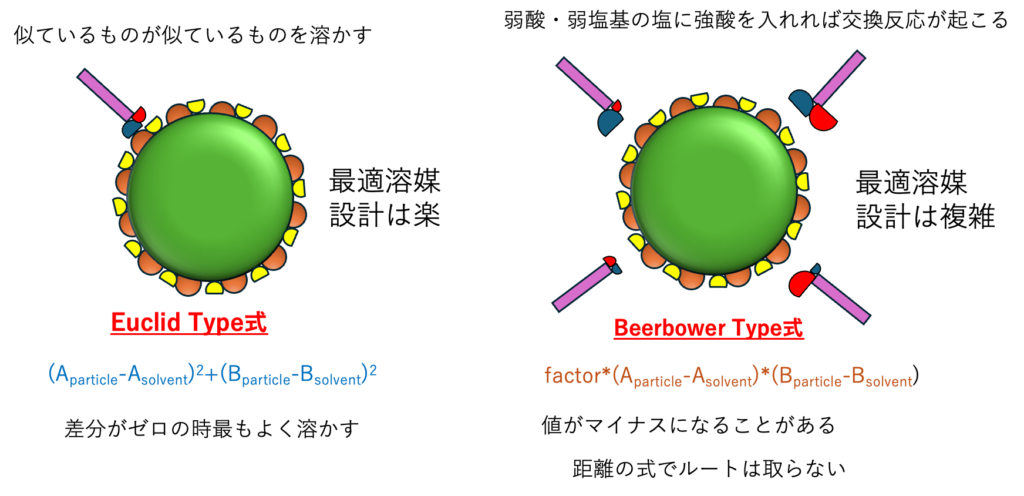
そこで酸塩基相互作用は2つのタイプの式を適用する。
似たものは似たモノを溶かすというEuclid Typeの式では、差分がゼロの時に最も良く溶解・分散するので最適溶媒設計は楽だ。
酸同士の差分、塩基同士の差分を掛けるBeerbower Typeの式では、酸塩基の大小によって付合が複雑に変わる。さらにfactorにも付合がある。
ケースによっては距離の式がマイナスになる事もあり、最適溶媒設計はとても難しくなる。変数が多く、式の自由度が高いので、データが少ない場合どうとでもなってしまう危険性を孕んでいる。結果をよく見て判断する必要がある。
立体障害は?
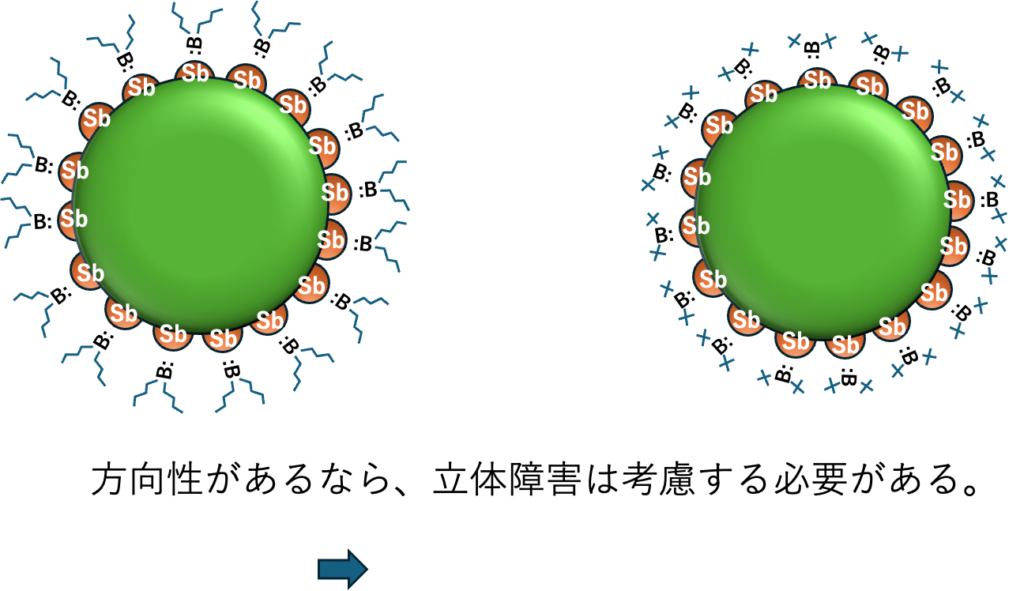
方向性があるなら立体障害は考慮する必要があるが、現状では未対応だ。
代表的な4化合物
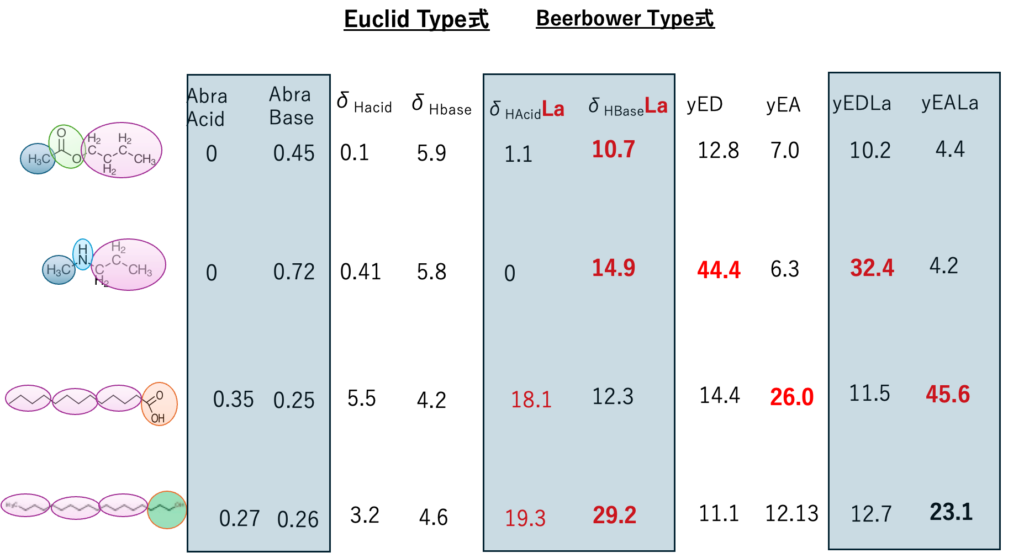
33式を皆んな計算してしまう

実例でやってみよう
YMB24Pro4MIを持っている方は実際にやってみよう。
データの作成、計算の実行は文字で説明するとすごく難しい。V-tubeを久しぶりに作ってみた
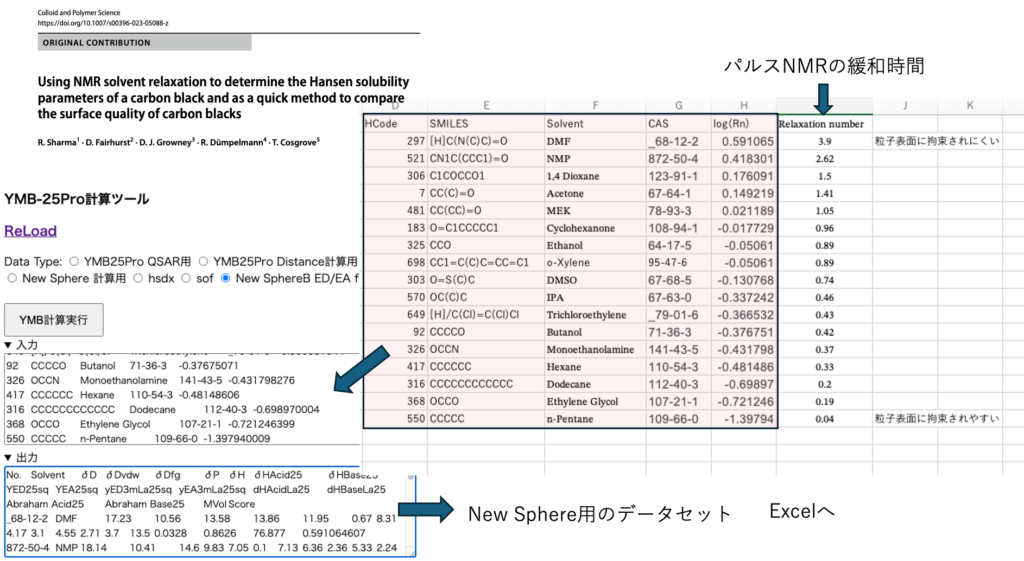
例題はパルスNMRを用いたカーボンブラックの表面解析だ。パルスNMRの緩和時間(RN)と溶媒種(CAS#)の一覧をExcelに作成する。YMB24Pro4MIのデータ変換機能を使えば簡単にYMB計算用のフォーマットが得られる。2列目がSmilesの構造式、5列目がlog(RN)であれば後はX印でも良い。このテーブルをコピーし、YMB-25Pro計算ツールにペーストする。そしてオプションでNew SphereBを選択して計算を実行する。
出力をエクセルに戻す。
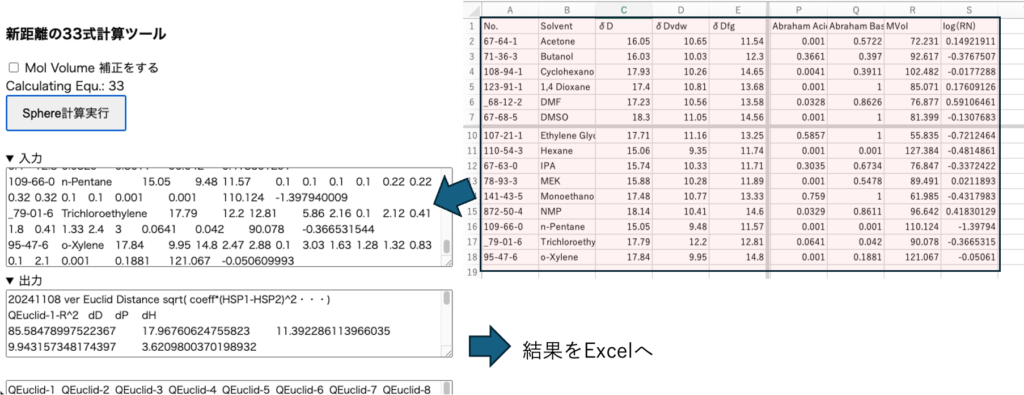
その結果を新距離の33式計算ツールにペーストして計算を実行する。このプログラムは5コアを使って計算するが、それでも5分ほどかかる。計算が終了すると2種類のアウトプットが出力される。それらをExcelに戻す。
新しい距離の33式
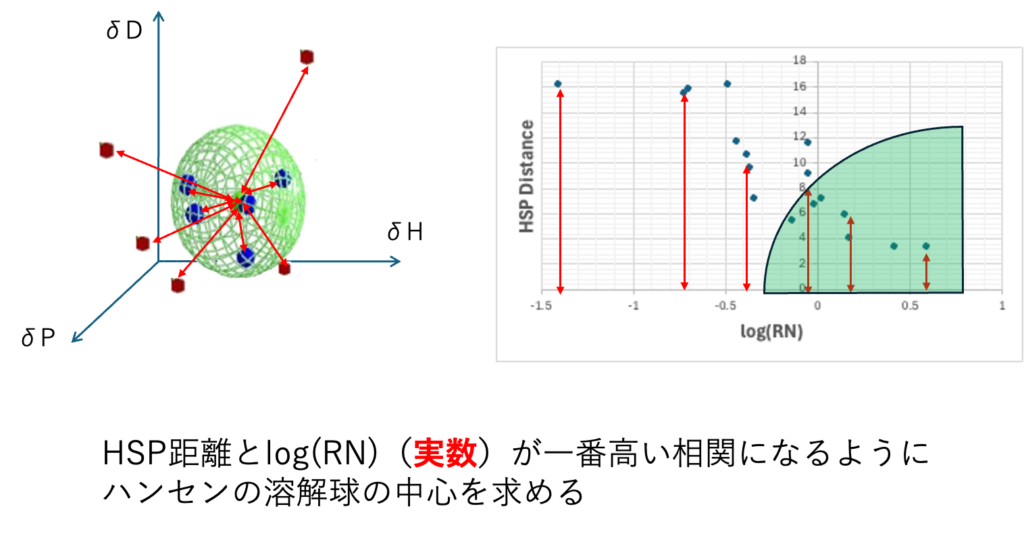
この場合は緩和時間は実数なので、33式計算ツールはHSP距離とlog(RN)が一番高い相関になるように溶解球の中心を探索する。相関係数は一つ大きく外れるものがあると、とても小さくなる。また自分が欲しい領域の精度を上げることはできない。つまりRNが大きい部分、逆に小さい部分を精度良く求めたい、には対応できない。相関係数の値だけで評価するのは危険である。そこで、実際にグラフを書いて確認するのが良い。
33式のグラフ・ビュアー

計算結果を2DViewerツールにペーストすると横軸にlog(RN), 縦軸にHSP距離が表示される。
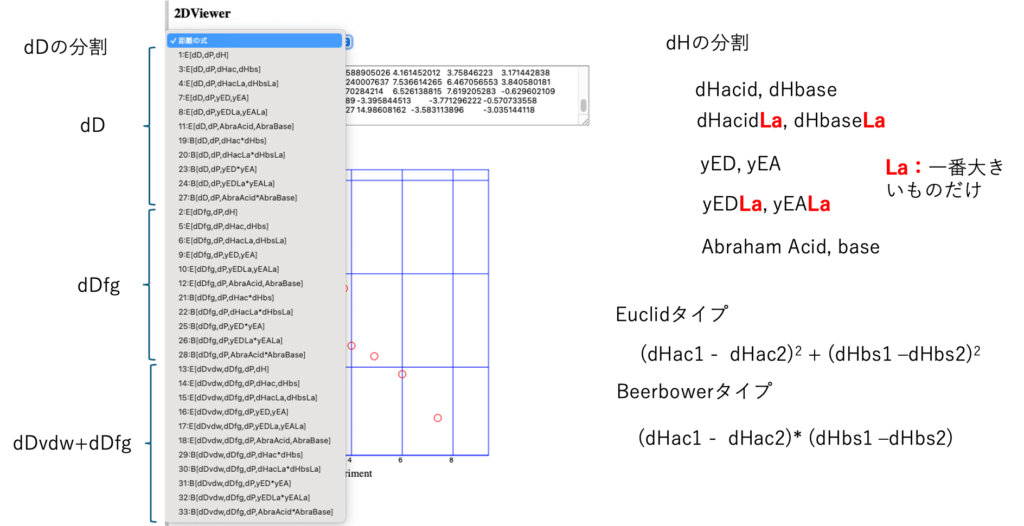
Selectorを使って距離の式を選べばグラフが表示される。グラフの点をクリックすれば名称が表示される。
実際にやってみよう
sqrt(4.0*(dD1-dD2)^2+(dP1-dP2)^2+XXX) Euclid
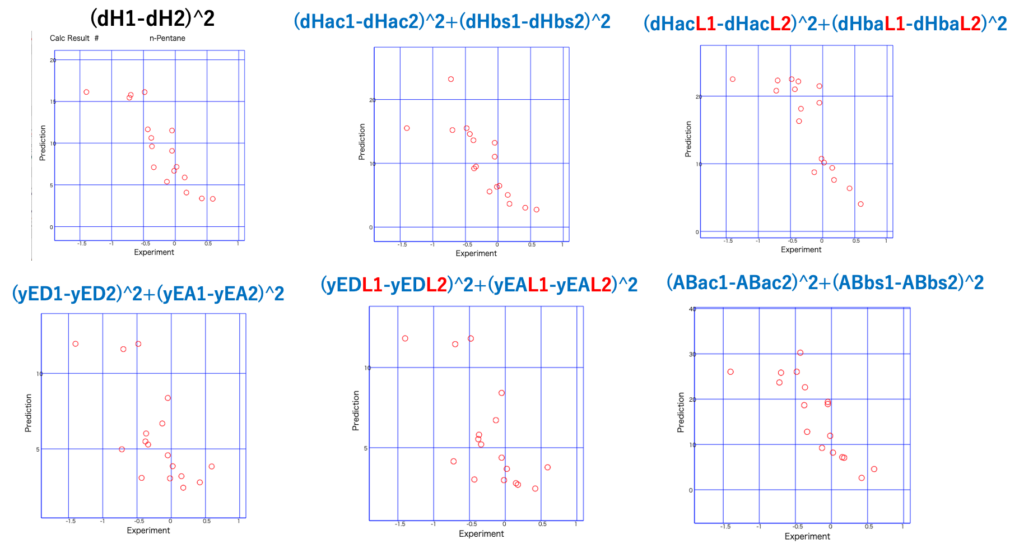
意外とdHを分割しない(dH1-dH2)2でも相関係数的には良い結果を与えている。
どこに注目するか?
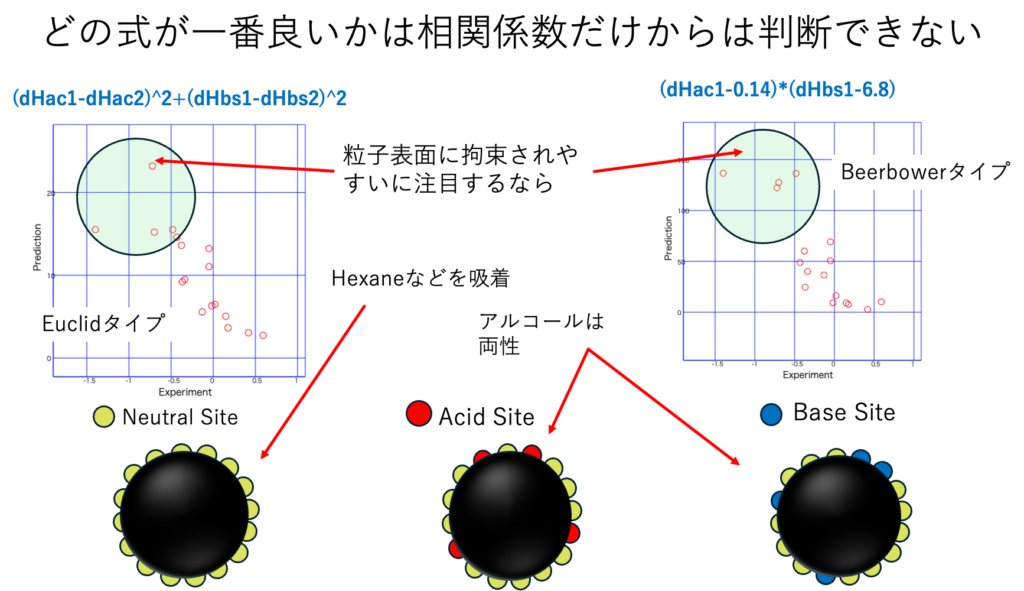
粒子表面に拘束されやすい溶媒には、アルコール系と炭化水素系の2種類がある。この二つのHSPは大きく異なる。その2つが表面に拘束されやすいのであれば、活性炭のように、中性の部分と酸点、塩基点が存在するのかもしれない。距離が長い部分を解釈したいならBeerbowerタイプを選んだ方が良い。
HSPは良溶媒がハンセン空間の球を作る
この場合、どんな溶媒がハンセン空間の中で集まっているのだろうか?
良分散させる溶媒だろうか?
HSP距離の短い化合物は緩和時間の長いものになる。
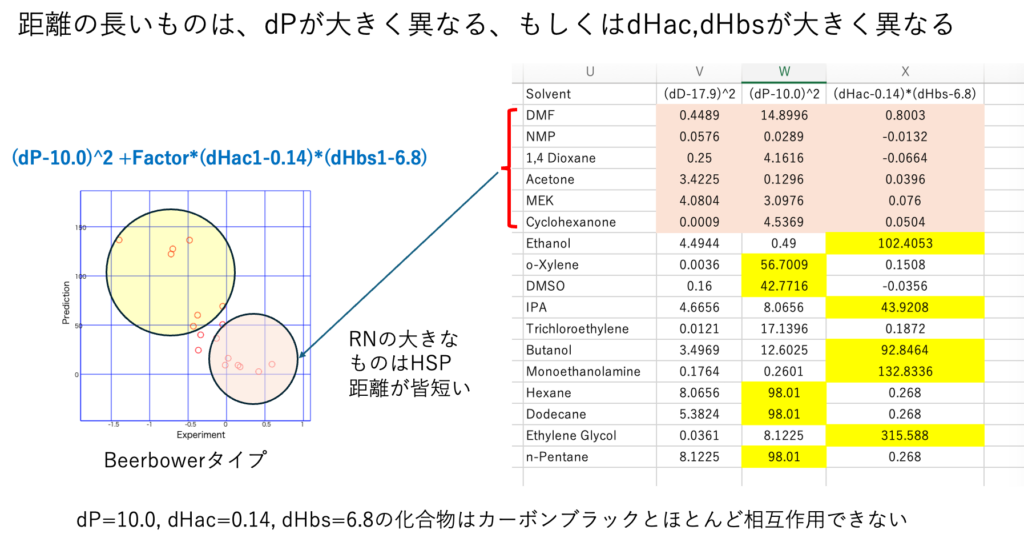
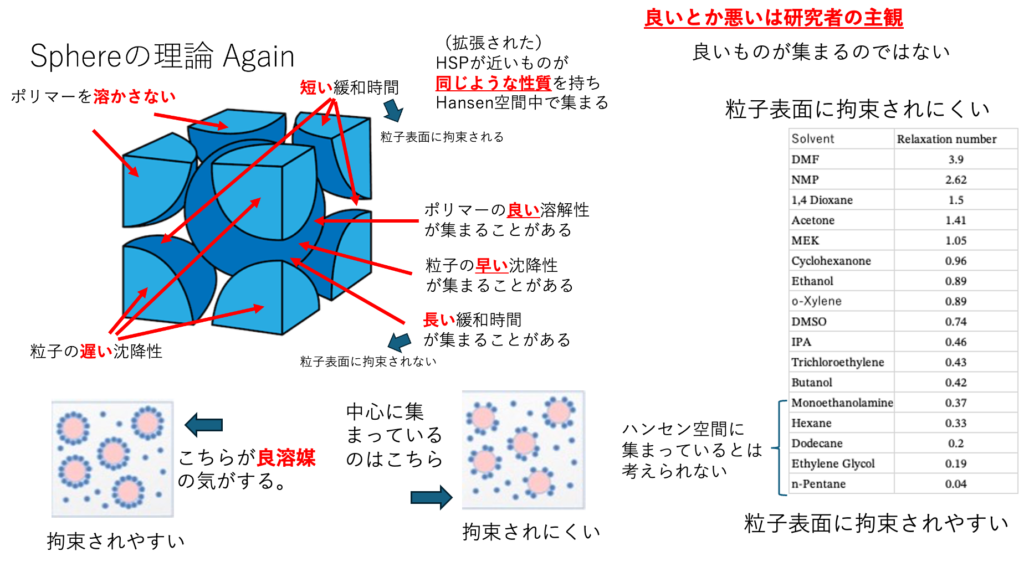
我々は、拘束されやすい溶媒は粒子表面をきれいに取り囲み、凝縮を妨げ、分散安定性を高めるような気がする。しかし、HSP空間に集まっているのは、拘束されにくい溶媒であることがわかる。良溶媒とは研究者の主観だ。良溶媒が集まるのではない。HSPが近いものが同じような性質を持ちHansen空間中で集まる。それがSphereの理論だ。
HSPiPでこの問題を解こうとする場合、拘束されやすい溶媒のScoreを1にしたくなる。
その場合、HSPが大きく異なる炭化水素系溶媒とアルコール系溶媒両方が良溶媒になるので、Double Sphere法(Sphereの中心が2種類ある)を使うことになる。
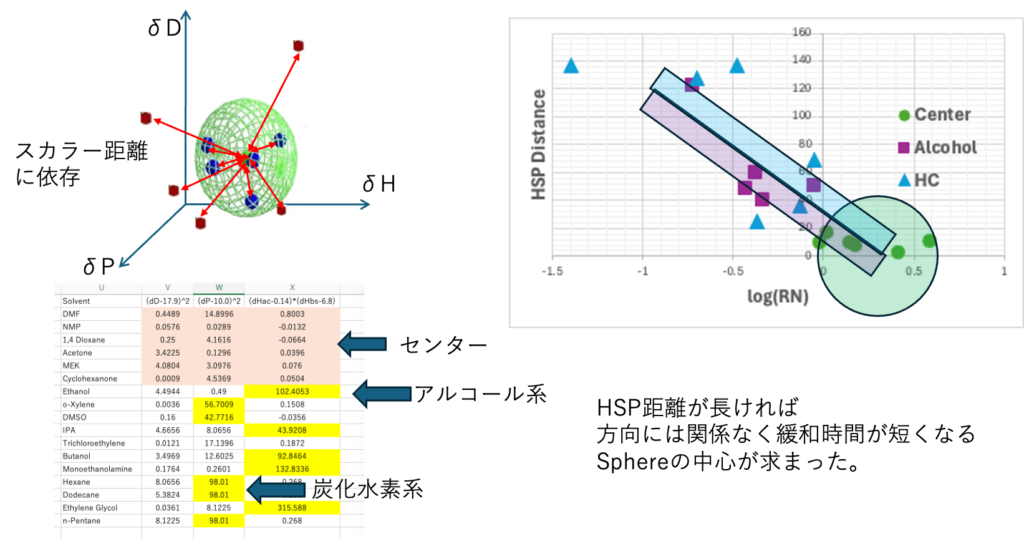
中心から遠くなると、方向にはよらず、離れた距離のスカラー量にしたがってlog(RN)が短くなる。
それではC60ではどうなるだろう?
CBと異なり、表面は完全に均質だ。
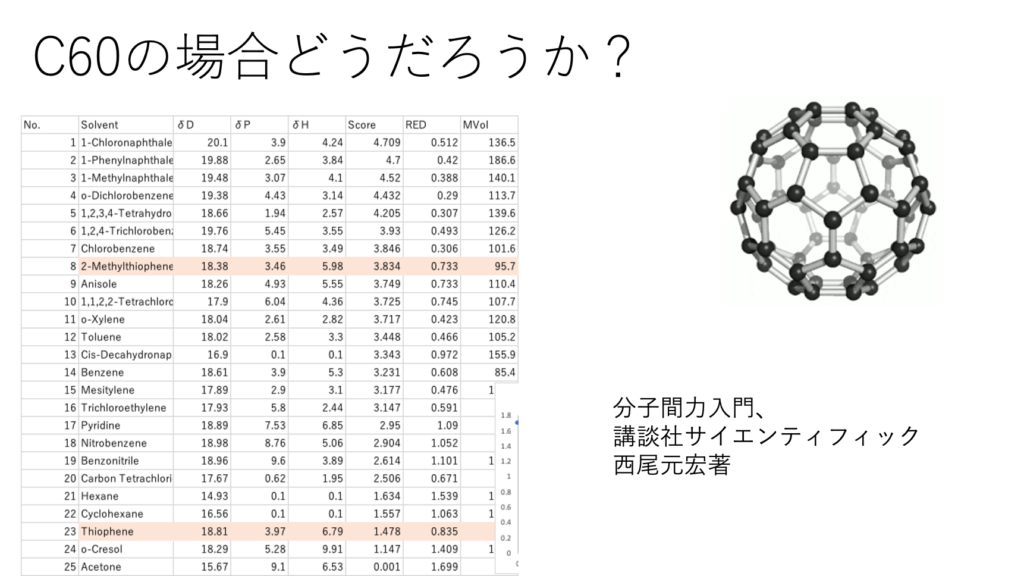
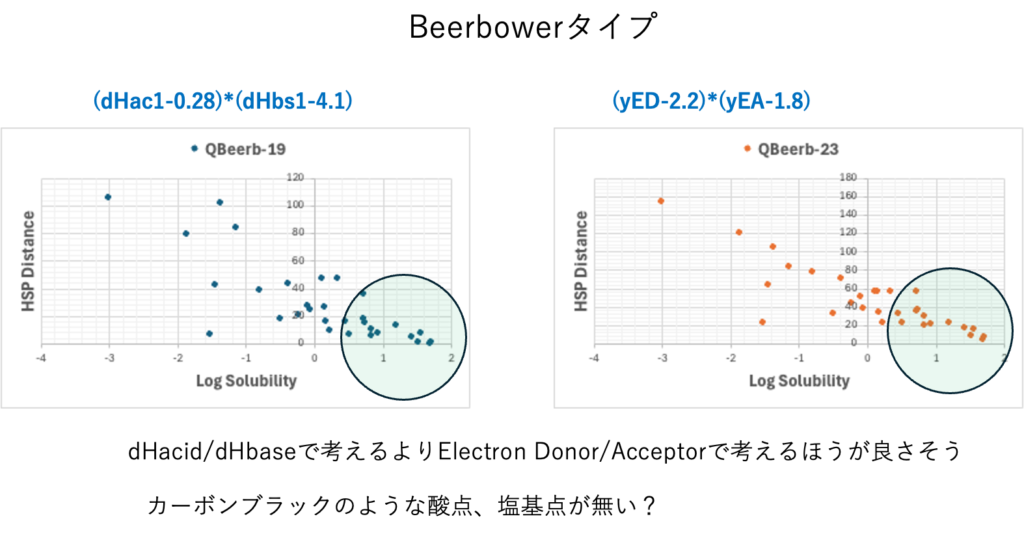
CBではBeerbowerタイプのdHacid/dHbaseで考えるのが良かった。C60ではyED/yEAで考えた方が良さそうな事がわかる。これはC60の表面はπ電子雲に均質に囲まれた材料であるからと考えられる。
距離の式を33個も作る理由
HSP距離と目的の物性値の相関が高ければ、より良いモノを逆設計できるというメリットがある。
しかし、これまで30年間MIをやってきた身としては、この程度の少ないデータでこの式が一番よくて、逆設計するとこれが一番だとは、なかなか言えない。
33式も評価するのは、式の意味することから、溶解・分散の機構を知る事だと考えている。
YMB24Pro4MIのユーザーはそこの所をきちんと理解してほしい。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください。
