2024.7.18
解析例トップ >
次世代HSP技術 >
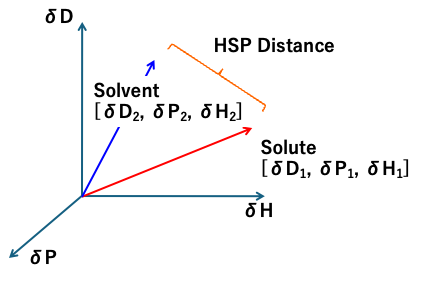
HSP距離
例えば溶質[δD1, δP1, δH1]と溶媒[δD2, δP2, δH2]のHSP距離は
HSP distance (1967)={4*(δD1-δD2)2 + (δP1-δP2)2 + (δH1-δH2)2 }0.5
で計算される。
ここにある、δDの前にある4と言うFactorは、いろいろ議論があったが、私の考えはHSP50周年記念講演会で発表した。本来、δDはファンデルワールスの大きから来るδDvdwと分子を構成している原子団から定まるδDfgとの合成ベクトルであった。
希ガスは、それぞれ原子の大きさに由来する蒸発潜熱を持つ。つまり溶解度パラメータを持つ。しかし、分子同士の相互作用は持たないδDfg=0と定義する。（当然、希ガスはδP、δHはゼロである。）
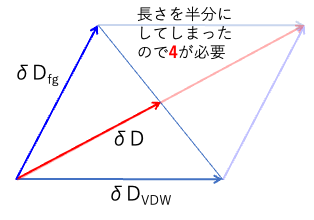
Distance2017 = {(δDvdw1-δDvdw2)2 +(δDfg1-δDfg2)2 + (δP1-δP2)2 +(δH1-δH2)2}0.5
そこで新しい距離の式を定義すると、δDの前にある4と言うFactorはいらなくなる。
さらに、HSP50周年記念講演会では水素結合項のElectron Donor/Acceptorの分割を発表している。
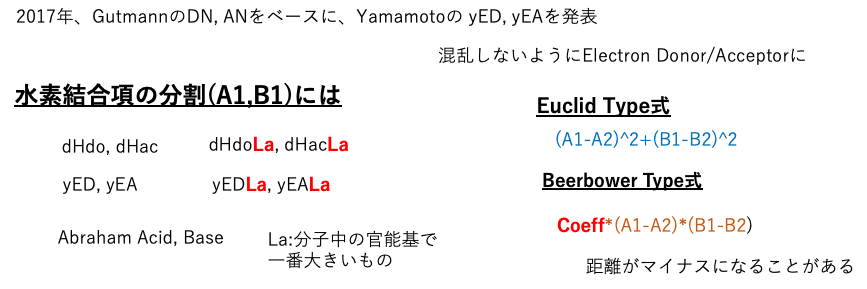
自分でやっておきながら、現在、33種類の距離の式と格闘する羽目になっている。
フローリー・ハギンスのカイ(χ, Chi)・パラメータとHSP
ハンセン先生の著書には次のように書かれている。
A1,2={ (δD1-δD2) +0.25*(δP1-δP2)2 +0.25*(δH1-δH2)2} (2.12)
χ12=V*A1,2/RT (2.13)
式2.12はクラッシックなHSP距離そのものなので、ポリマーと溶媒のHSPがあれば、χ・パラメータは計算できる。
それでは、33種類のうち、どの距離の式がχ・パラメータを推算するのに適しているのだろうか？
結論は、ポリマーごとに異なるとしか言えない。
HSPiPに搭載されているポリマーの溶解性の例題
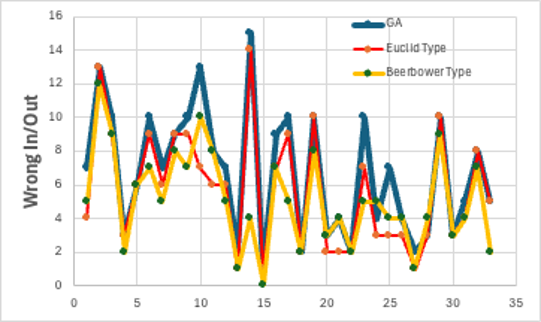
Wrong In/Outの数だけからはBeerbower Typeの式の方が少し良い。
Wrong In/Outが最小になる式のタイプでは次のものが選ばれた。
Euclid Type
1: sqrt(4.0*(dD1-dD2)^2+(dP1-dP2)^2+(dH1-dH2)^2) 36%
2: sqrt( 4.0*(dD1-dD2)^2+(dP1-dP2)^2+(dHacid1-dHacid2)^2+(dHbase1-dHbase2)^2) 30%
3: sqrt((dDvdw1-dDvdw2)^2+(dDfg1-dDfg2)^2+(dP1-dP2)^2+(dH1-dH2)^2) 18%
Beerbower Type
7: 4.0*(dD1-dD2)^2+(dP1-dP2)^2+coeff*(dHacid1-dHacid2)*(dHbase1-dHbase2) 39%
10: 4.0*(dD1-dD2)^2+(dP1-dP2)^2+coeff*(Y-ED1-Y-ED2)*(Y-EA1-Y-EA2) 42%
例えば、フェノール樹脂のようにポリマー自体に酸性を持つような溶質は、Classicな距離で溶解性を見てはダメだと言うことだ。
HSP距離の定量的解析
もし、溶媒とポリマーのχ・パラメータの組みがあるのであれば、χ・パラメータの逆数(良溶媒はχ・パラメータが小さい）をScoreに入れて、定量的に距離の式を作ってしまうことができる。これはあくまで、そのポリマー特有の距離の式であり、一般化はできないが。
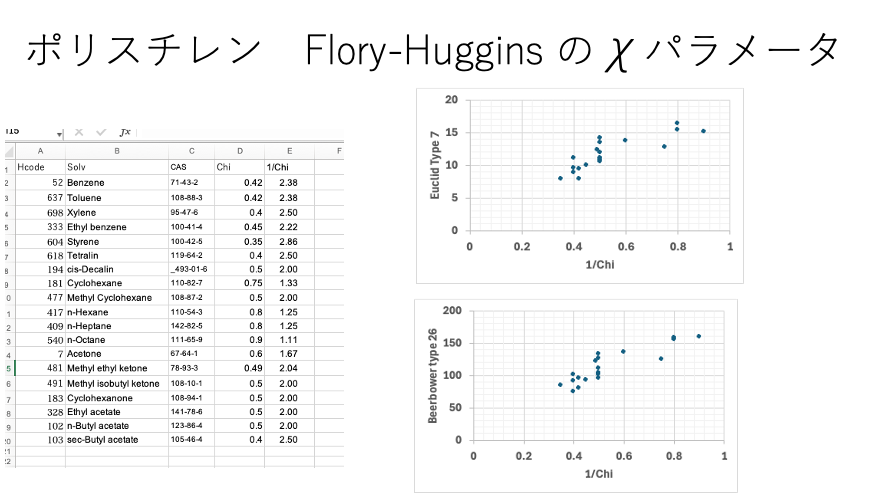
Euclid Type 7の式とBeerbower type 26の式が相関が高かった。
このχパラメータの予測式が得られれば、後はポリマー用の溶媒を片っ端から評価すれば良い。
MI的に考えるなら。
ポリスチレンの溶媒は多くの研究例がある。その多くは、溶解、不溶の0,1である。
それに対して、今回作成した33式全部で評価するのは大事である。たかだか19個のデータから作った式だ。この溶媒群で高い相関係数が、より広い溶媒群で成立するかどうかはわからない、χパラメータとScore 0,1の評価の一致度で33式の中の一番良い式を選べば良い。
おまけ
Mark–Houwink 式というポリマーの固有粘度を表す式がある。
[η]＝K・Mα
αが1で良溶媒、0.5で貧溶媒とされる。
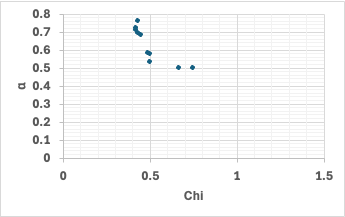
χパラメータとark–Houwink 式のαには(logとれば）高い相関がある。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください