2024.7.13
pirika.comで化学 > 化学全般
> 次世代HSP2, Pirika Pro for MI > その溶解はHSP依存だろうか?
> ハンセン溶解度パラメータ (HSP) Doc
注意:HSPiPに搭載の機能ではありません
溶解性、分散性を検討するのにハンセン溶解度パラメータ(HSP)を使う例はとても増えてきている。HSPの開発者としては、研究者冥利に尽きる。でも時には立ち止まってよく考えよう。
種本はパルスNMRを使った無機物の分散の論文を使ってみよう。
Fast NMR relaxation, powder wettability and Hansen Solubility Parameter analyses applied to particle dispersibility
David Fairhurst, Ravi Sharma, Shin-ichi Takeda, Terence Cosgrove, Stuart W. Prescott
Powder Technology 377 (2021) 545–552
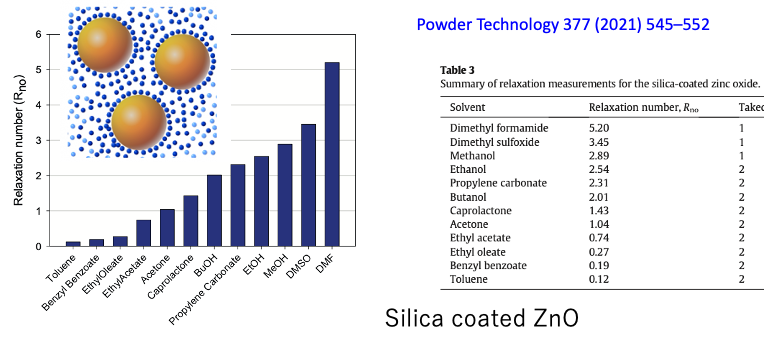
1:分散はHSPで説明できる説
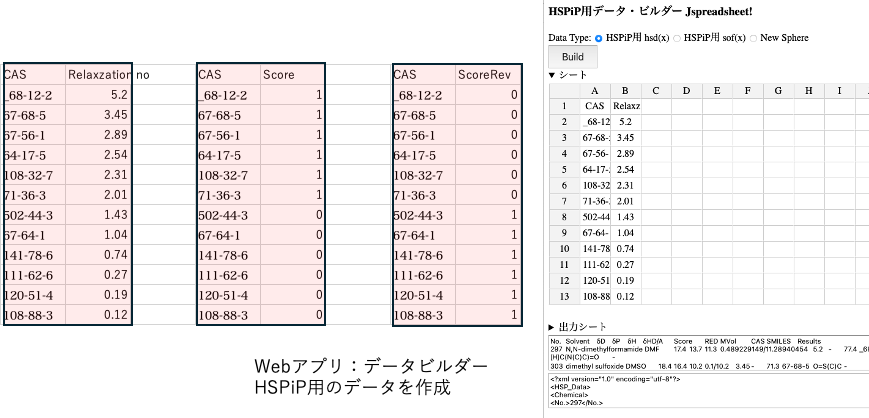
Webアプリを使ってHSPiP用のデータを作り読み込む。
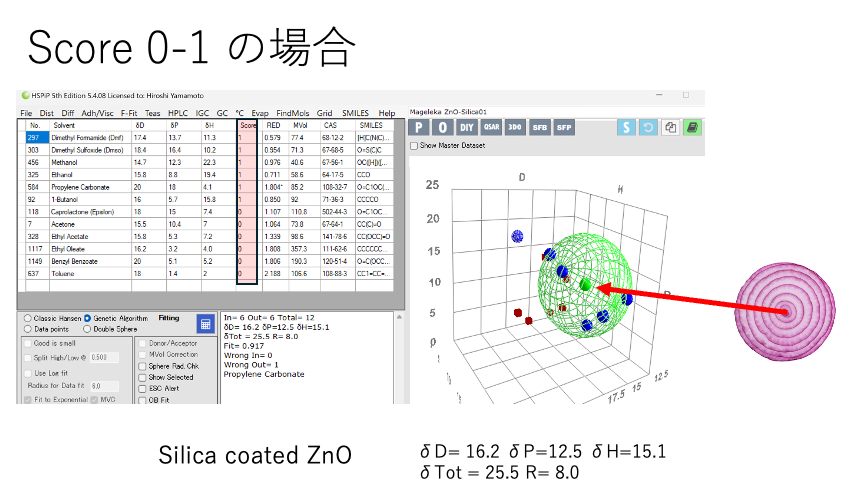
緩和時間は1/Relaxation Noになる。
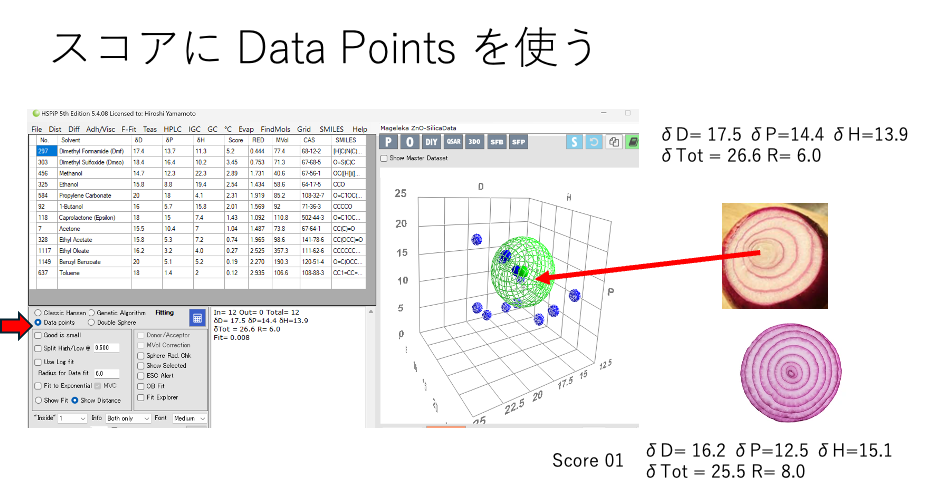
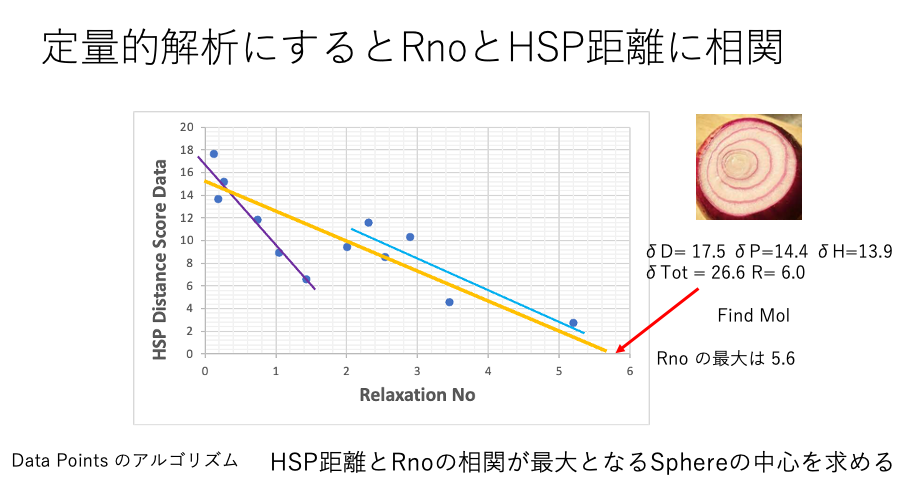
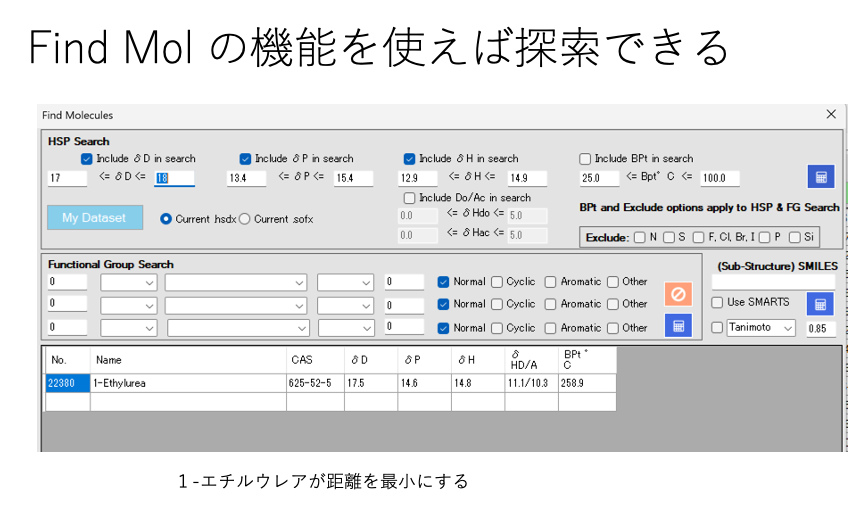
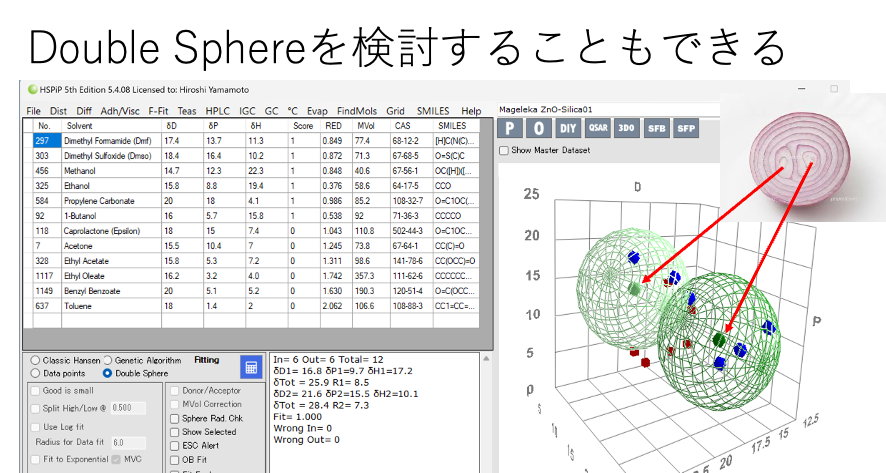
解析に特に矛盾もないので、HSPだけで溶解、分散が理解できると言ってもいい。
(緩和時間が短い方が粒子に束縛されやすいというのとは逆のような気がしていて、最近悩んでいる。緩和時間は1/Relaxation Noになる。緩和ナンバーが大きいものは緩和時間が短く粒子に束縛されやすい。あースッキリした)
2:HSPは必要ないと言う説
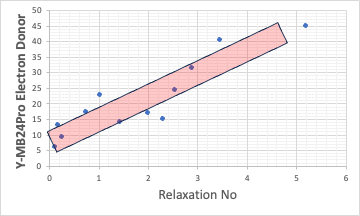
この溶媒をY-MB24proで計算する。yED(Yamamoto Electron Donor)とプロットすると綺麗な相関がある。何かをスクリーニングする時には、単一パラメータの方が有利だ。
HSPiPで計算された距離の式がなるべく短くなる。
HSP距離 = sqrt(4*(dD-17.5)^2+(dO-14.4)^2+(dH-13.9)^2)
1:HSPが[17.5, 14.4, 13.9]である溶媒を探索したらいいのか?
2:なるべく大きなyEDの溶媒を探索した方がいいのか?
どちらが正しいとは言えない。
しかし、2のアプローチはツールが少なく余り検討されてこなかった。
MAGICIAN的な取り扱い
HSPiP用のデータを作成する時にはCAS番号とScoreのペアを用意した。このCAS番号があると、データ変換のwebアプリを利用できる。CASやHcodeからSmilesや名称へ変換できる。
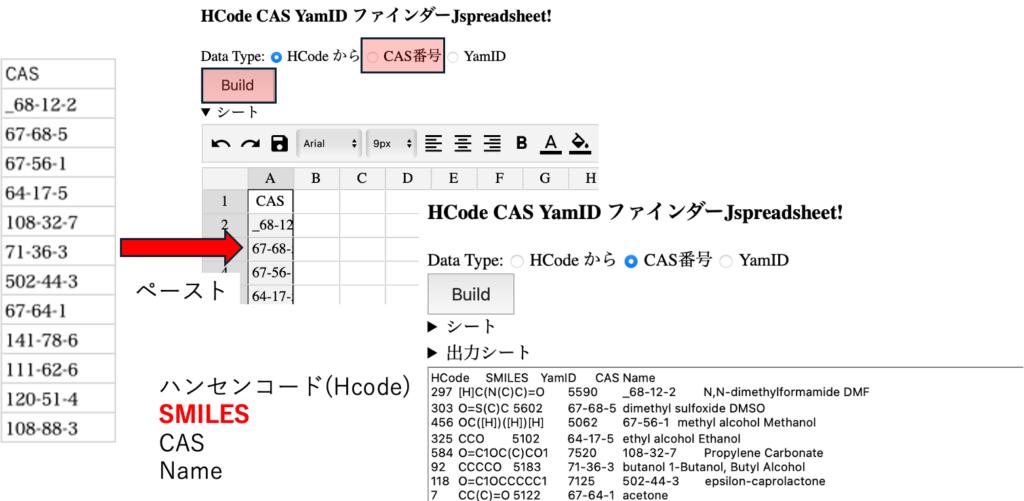
つまり、CAS番号があればSMILESの構造式が得られる。
化合物のSMILESから、3つのタイプの識別子を作り出すwebアプリが用意してある。
1つ目はY-MBだ。HSPとさまざまな熱力学的物性値が得られる。
この識別子がわれわれの独自であり、他のMIを使うGrに対する優位な点になる。
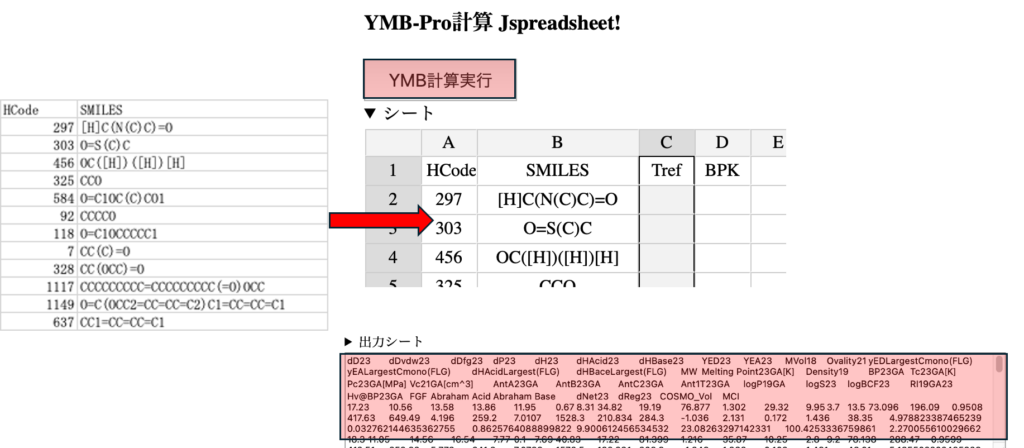
識別子が38種類生成される。

同じようにSMILESの構造式から、トポロジカル・インデックスの識別子をRDKit webアプリが作り出す。全部で39のパラメータを作り出す。
CNDO/2とQeQ電荷平衡法の計算もSMILESの構造式から計算できる。このWebアプリも39の識別子を作成する。
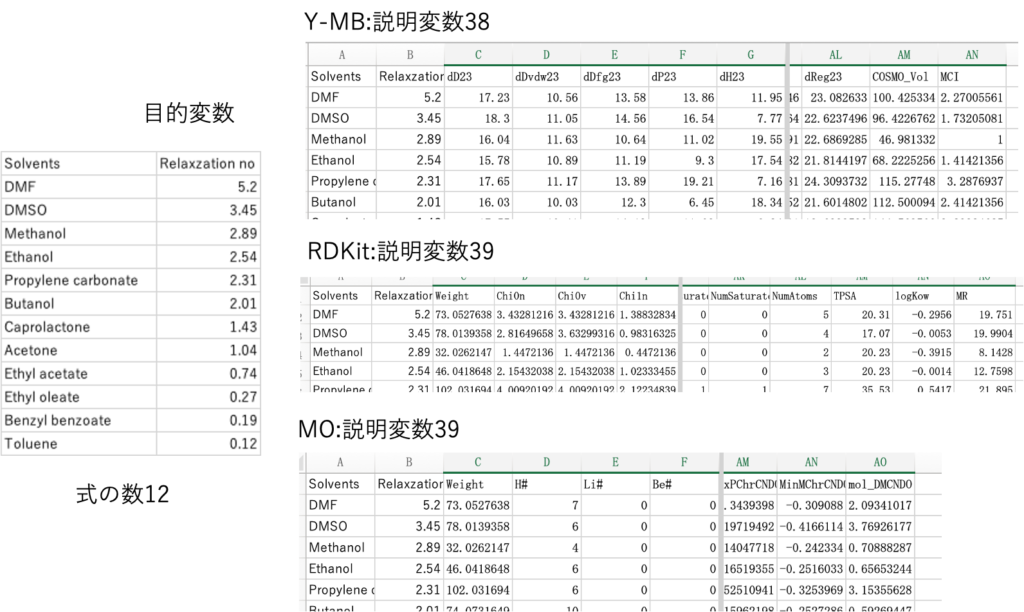
このような目的変数と説明変数の組みがすぐに得られる。
Pirika24Pro4MIで変数選択重回帰法を使う
目的変数は、いろいろな溶媒の緩和ナンバーになる。
説明変数は、Y-MBで38, RDkitで39, MOで39説明変数がある。
つまり、目的変数に対して説明変数が圧倒的に多い。
そのような場合、多くの場合、PCA(主成分分析)、PLSなどを使って次元削減しモデルを作成する。Y-MB, RDkit, MOの3つのテーブルについて次元削減しモデルを作ることはできる。
PCA回帰については他で説明する。
ここでは、変数選択重回帰のWebアプリを解説する。
HSP距離 = sqrt(4*(dD-17.5)^2+(dO-14.4)^2+(dH-13.9)^2)
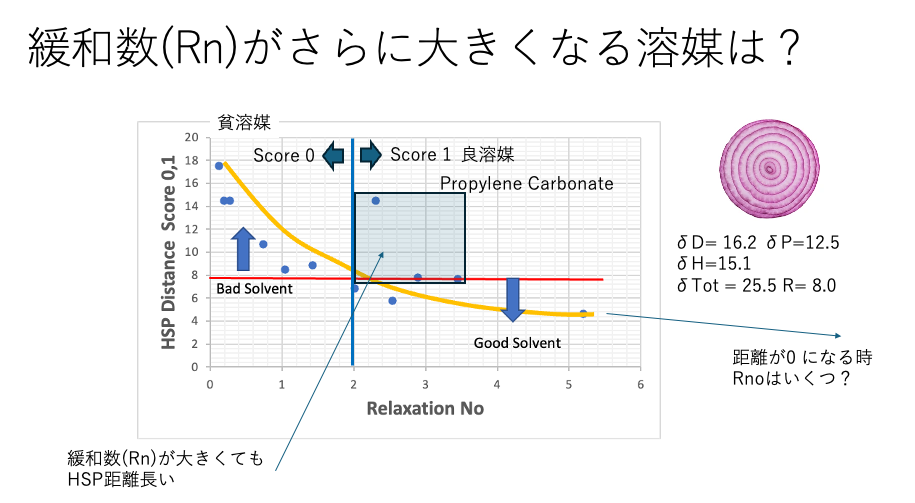
HSP距離が短ければ緩和ナンバーが大きくなる。
溶媒のHSPがわかれば緩和ナンバーは計算で出すことができる。
それでは、例えばY-MBの38種類の説明変数から緩和ナンバーの予測式を作るにはどうしたら良いだろうか?
連立方程式を解くときのことを考えると、式が12個あるなら最大でも説明変数は12になる。38変数から12個の変数を選ぶには、38C12の場合の数がある。それを調べるのも可能であるが、ここではもっとシンプルな方法を試す。
緩和ナンバーを説明するのに、38説明変数のうち、どの変数が重要かを調べる。
変数を2個選び、回帰式を作る。その時の相関係数を計算する。変数を3つ、4つと指定して回帰式を作成する。

全ての組み合わせを計算し、相関係数によってソートする。
どれでもyEDLaが選ばれるので、これが重要だとわかる。
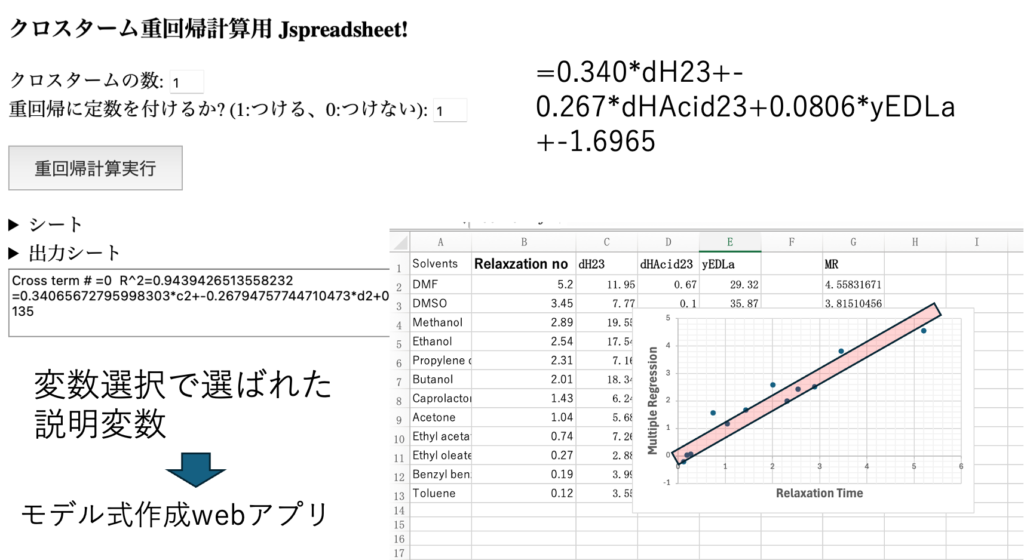
クロスターム重回帰計算Webアプリで、変数選択された項目からモデル式を作ることができる。ここでは、あえて、dH, dHacid, yEDLaを選択した。
MVol, COSMO-Vol, MCIの3つの説明変数でも同じレベルの物性推算モデルを作成できる。
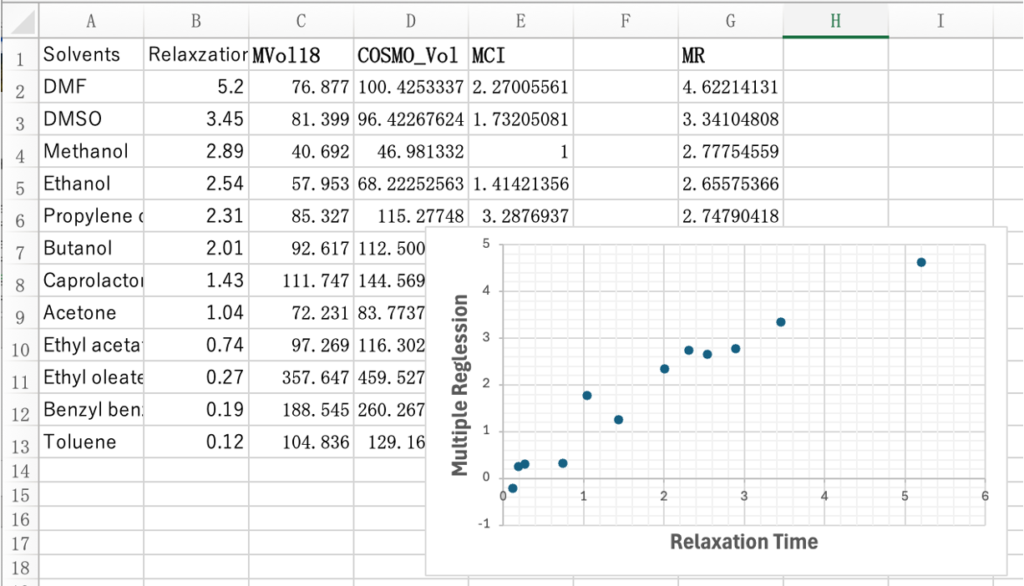
つまり、溶解性、分散性のモデル化にHSPは必須ではないということだ。
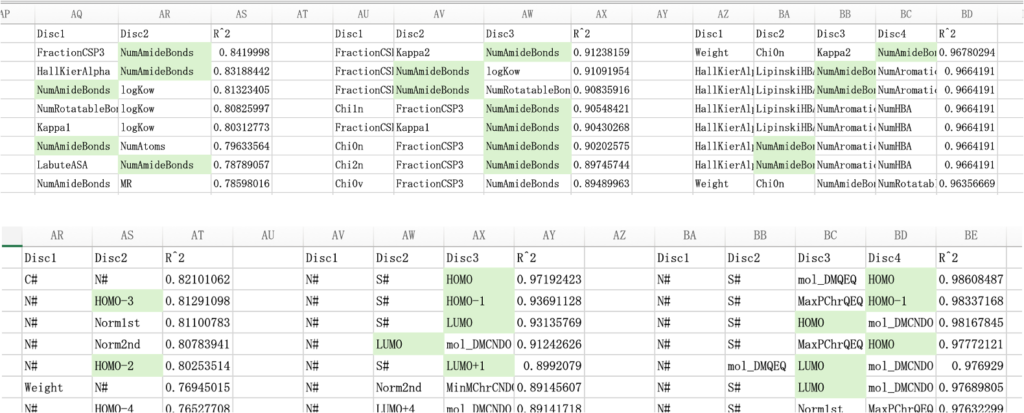
RDKitの識別子を使った場合にはアミド基の数が重要なことがわかる。
分子軌道計算や電荷平衡法の計算結果を使う場合にはHOMO, LUMOが重要なことがわかる。
つまり、HSPを使わなくても、溶解性や分散性を記述でるということだ。
MAGICIANであるために
HSPにこだわらずに、使えるパラメータは全て利用してモデルを考える。
特にBig Dataを利用できない場合には必須となる考え方だ。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください
