2024.7.13
pirika.comで化学 > 化学全般
> 次世代HSP2, Pirika Pro for MI >ハンセンの溶解球の誤解:良いものが集まって球を作る。
> ハンセン溶解度パラメータ (HSP) Doc
注意:HSPiPに搭載の機能ではありません
良いものが集まるわけではない
カーボンブラックの分散に関して解析を行ってみよう。
種本は次の論文だ。
Using NMR solvent relaxation to determine the Hansen solubility parameters of a carbon black and as a quick method to compare the surface quality of carbon blacks
R. Sharma · D. Fairhurst · D. J. Growney · R. Dümpelmann · T. Cosgrove
https://doi.org/10.1007/s00396-023-05088-z
パルスNMRの緩和ナンバーはハンセンの溶解度パラメータと結びつけて解析されている。
2025.5.11:緩和時間と緩和ナンバーを混乱していました。緩和ナンバーは緩和時間の逆数です。
こうしたデータがテーブルにまとめてあるとする。
こうしたデータがあれば、すぐにMIツール(2024.12.24 Pirika24Pro4MIに変更)が使える。
ここでは、まずHSPiP用データ作成Webアプリ(MIツール)を使う
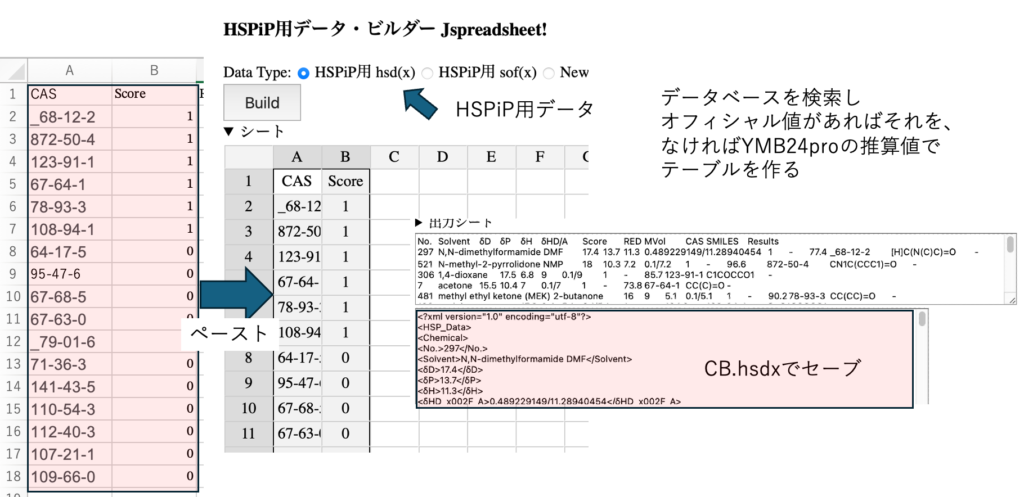
CASとScoreの組みをコピーしてWebアプリ(MIツール)にペーストして、Buildボタンを押すと、HSPiPで読み込めるxmlファイルを吐き出す。それを全てを選択して、CB01.hsdxとセーブする。このファイルはHSPiPで読み込むことができるので、すぐにHSPiPでの評価ができる。
HSPiPは他のソフトの連携が悪く、入力データを作るのは大変だ。1つ1つCAS番号から作り、Scoreを間違えなく入れなくてはならない。Scoreに実数を入れたり、Scoreを逆転するのは大変な手間になる。
そこで、CASとSCOREのペアからWebアプリ(MIツール)で入力データが作れると、とても労力を削減できる
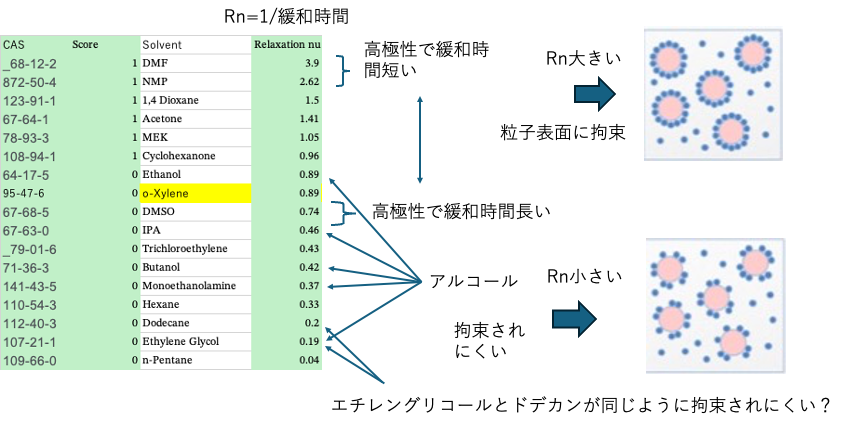
緩和ナンバーが大きいものをScore=1とし(大きいものが良いもの、Sphereの内側に来るという仮定)、ハンセンの溶解球を計算すると次のようになる。
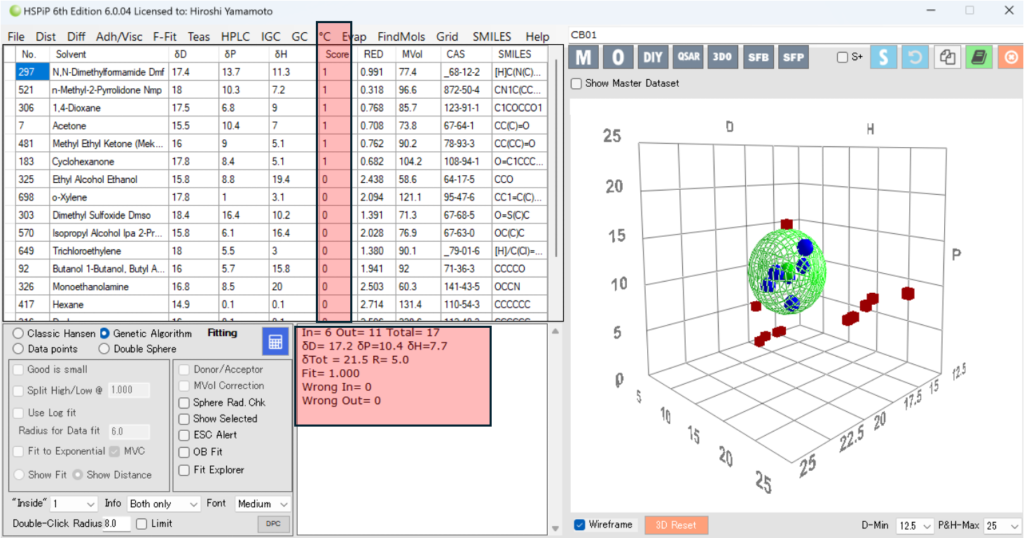
誤認識はなく、緩和ナンバーが大きくなる溶媒は青くマークされていて、ハンセン空間で集まっている。CBのHSPは[17.2, 10.4, 7.7]半径5.0になる。
著者の論文も同じような結果になっている。
パルスNMRは緩和時間が短いものが粒子の表面に拘束されていると判断される。緩和時間が短いものが、粒子表面をよく濡らすともいう。緩和時間の長いものは粒子表面にいない自由溶媒と分類される。
次に緩和時間が長いもの(粒子表面に束縛されにくい:緩和ナンバーは小さい)をScore=1と設定してSphereを計算してみる。
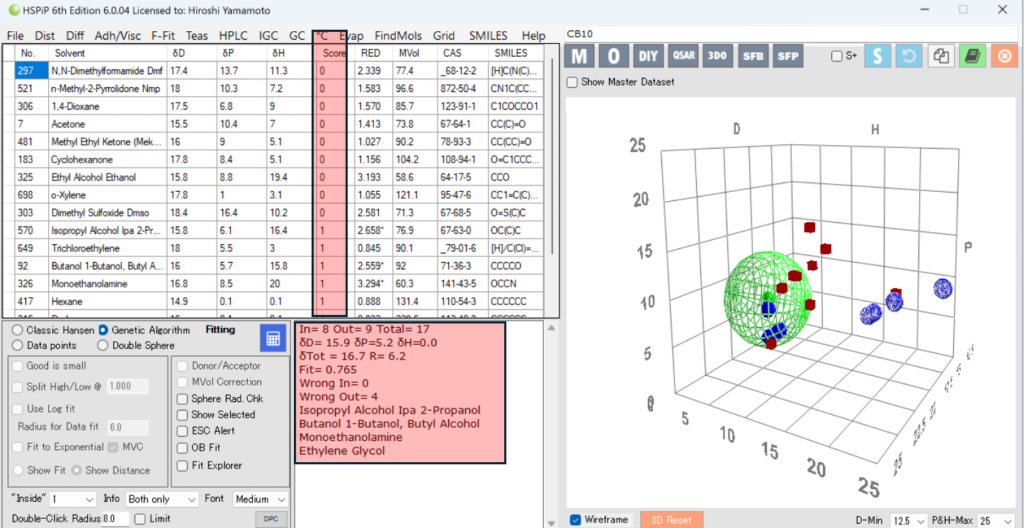
すると、間違って認識されるものが4つ現れる。
Sphereの中心は[15.9, 5.2, 0.0] 半径6.2になる。ペンタンなどの疎水性の化合物がこの領域である。エチレングリコールやアルコールが大きく外れる。
このような場合Double Sphereを使うことが多い。
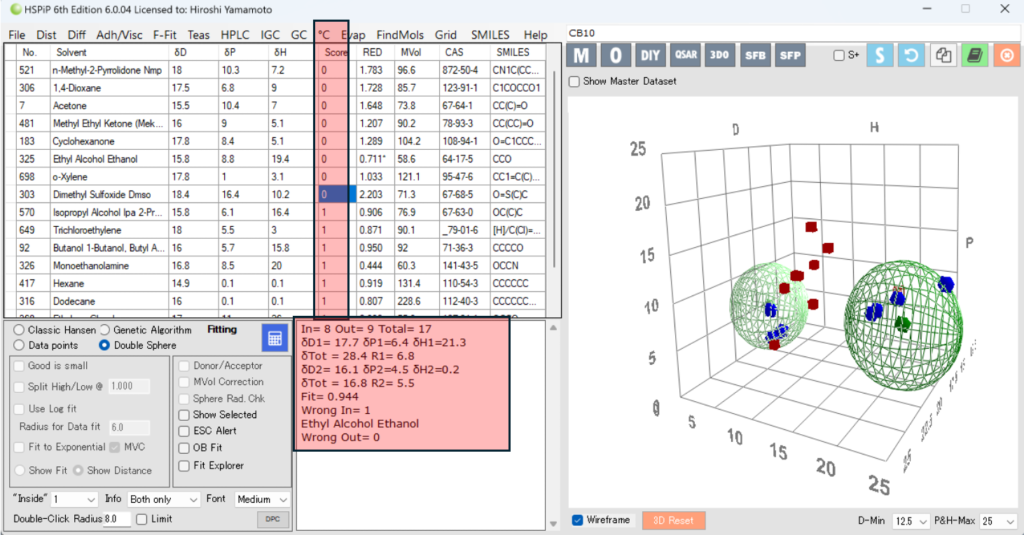
[17.7, 6.4, 21.3] 半径6.8
[16.1, 4.5, 0.2] 半径5.5
の2つのSphereが見つかる。間違って認識されるものは1つだ。
HSPが近いものが同じような性質を持ちHansen空間中で集まる
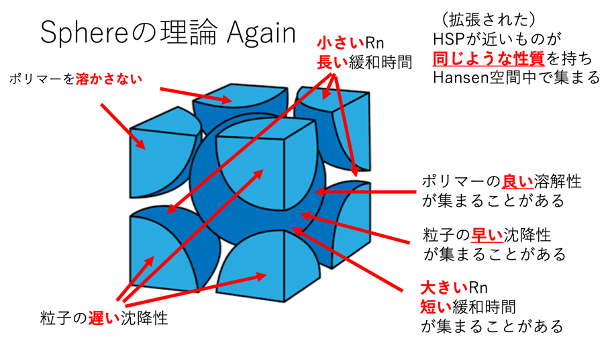
同じような性質が、研究者にとって都合が良いかどうかは関係ない。都合の良いものがScore=1ではない。
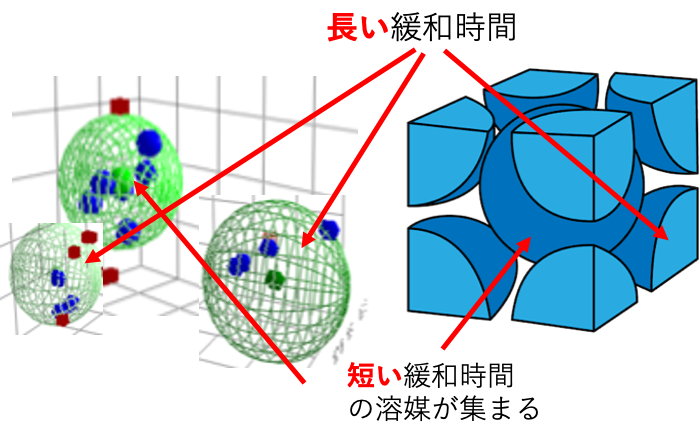
短い緩和時間(大きな緩和ナンバー)のものがハンセン空間の比較的中心に集まっているという言い方もある。
しかし、アルコール系統の長い緩和時間(小さな緩和ナンバー)が集まる領域と、炭化水素系統の長い緩和時間の集まる領域の2種類があるという言い方も可能である。
活性炭などは基本疎水的な化合物を吸着するが、酸点、塩基点を持つものもあり、2種類の表面を持つこともある。あくまでも解釈の仕方だ。
Scoreに緩和ナンバーの実数を使う。
緩和ナンバーが大きいものほど、HSP距離が短いという仮定で計算する。
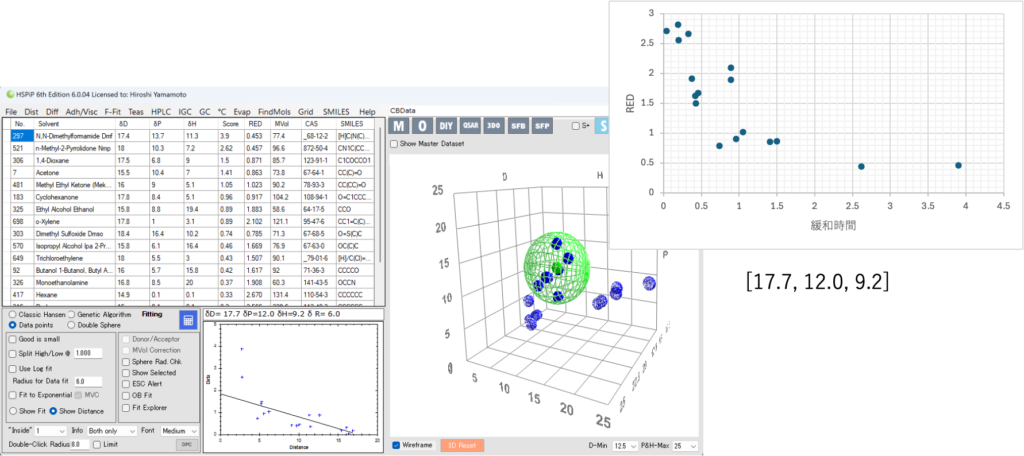
HSPが[17.7, 12.0, 9.2]の時にHSP距離がゼロになって緩和ナンバーが最大になると予測される。大まかにはHSP距離が短くなると緩和ナンバーが大きくなる傾向があることはグラフからわかる。横軸をlogを取ればより顕著だ。
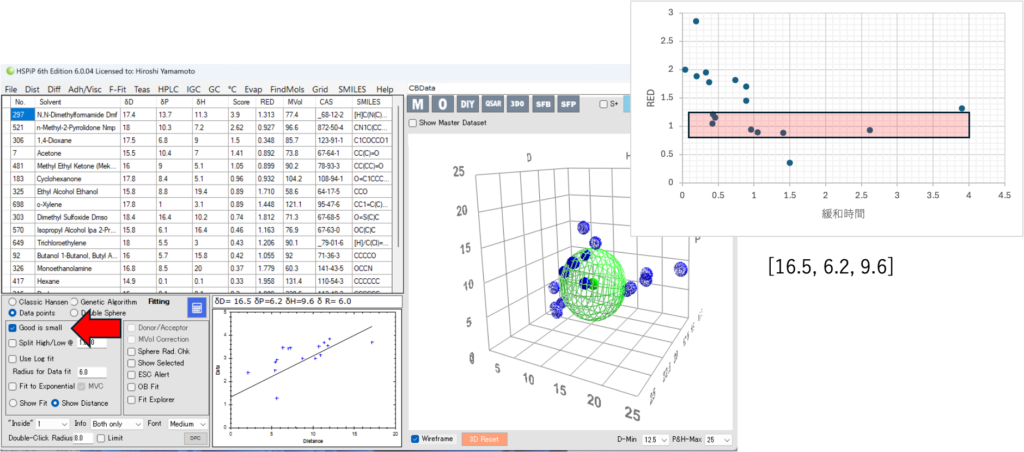
Data Pointsの解析では、Good is Smallのチェックを入れると、逆に緩和ナンバーが小さいものがgoodとなるSphereの中心を求める。ところが緩和ナンバーとREDのグラフでは、REDが小さい時に緩和ナンバーは小さくならない(私の計算結果とは大きく異なるのでHSPiPのバグかもしれない)。
同じREDであるのに緩和ナンバーが大きく変わるデータが多く存在する(赤いゾーン)。
ペンタンとアルコール両方がGoodになる。そこで求まったCBのHSPは[16.5, 6.2, 9.6]とハイドロカーボンとアルコールを足して2で割ったような値になる。溶媒のHSPが[16.5, 6.2, 9.6]の時にHSP距離はゼロになるので緩和ナンバーは一番大きくなるはずであるが、そのような結果はあり得ない。
Classic Hansen距離では理解できない
HSP距離=sqrt(4*(dD1-dD2)2+(dP1-dP2)2+(dH1-dH2)2)
全てが1つの式で評価できた時代は良かった。詳しいことはPirikaNews2024.07か新しいHSP距離の考え方 量子ドットを例に を読んでいただきたい。
理論的にどの式が最善かはわからないので、データ駆動型の研究方針で、片っ端から距離の式を作るWebアプリで評価し、評価が高かった距離の式を解析することで、「CBの分散で何が起きているかを考える」方針でいく。
式はEuclid TypeとBeerbower Typeの33式を評価した。
データの作成法、距離の式の求め方を説明
書いて説明するのは難しいのでV-tubeを作った。
緩和時間長い方がHSP距離が短いという設定では、Classic Hansen距離で十分であった。
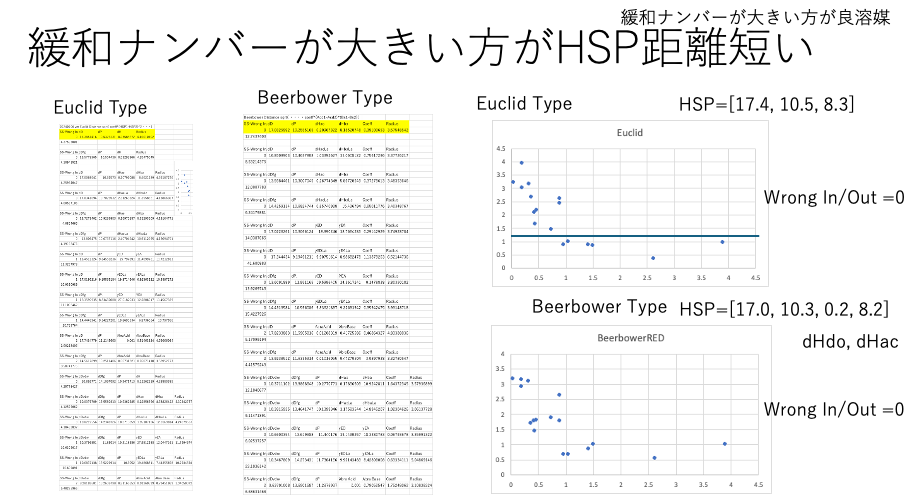
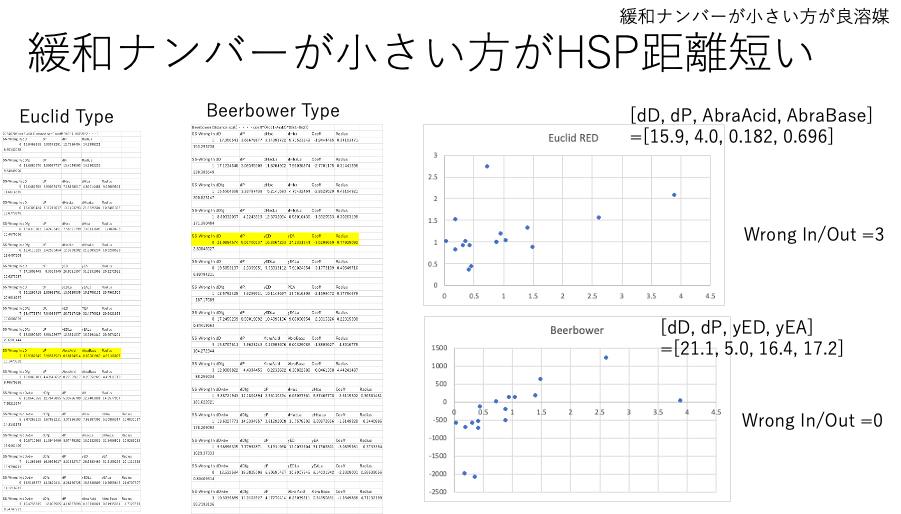
緩和ナンバーが小さい方がHSP距離が短い:こちらの解析では、HSPiPの解析結果とは全く異なる傾向が得られる。特にBeerbower Type の式を使うと、ペンタン、アルコールの違いを吸収した上で距離が短いものほど緩和ナンバーが小さくなった。Factorが入る分、複雑になり、逆の説明もできてしまう。
2024.7.17追記
QSphere:Scoreが実数の場合、実数と距離が一番高い相関を持つように距離の係数を決める。定量的解析法。
QSphereが使えるようになったので、緩和ナンバー自体をScoreに入れて解析を行った。
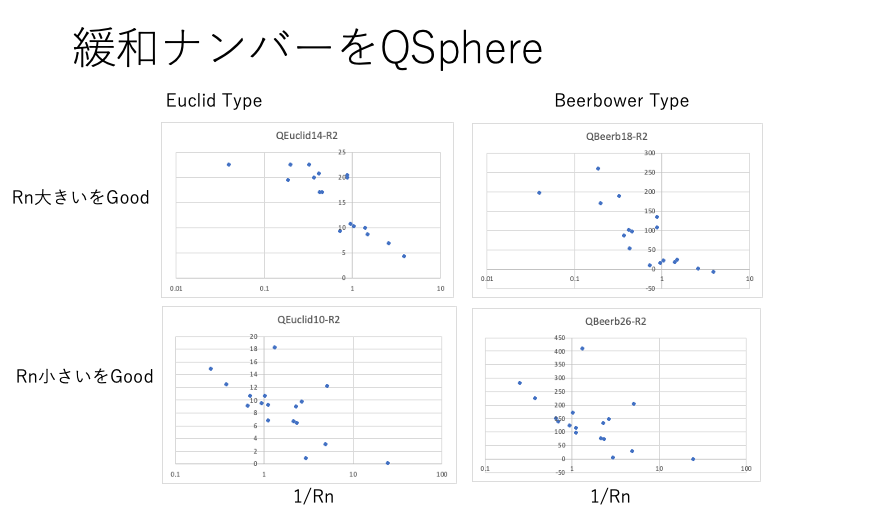
QSphereしてもRnが大きいものをGoodとした方が相関係数は高い。
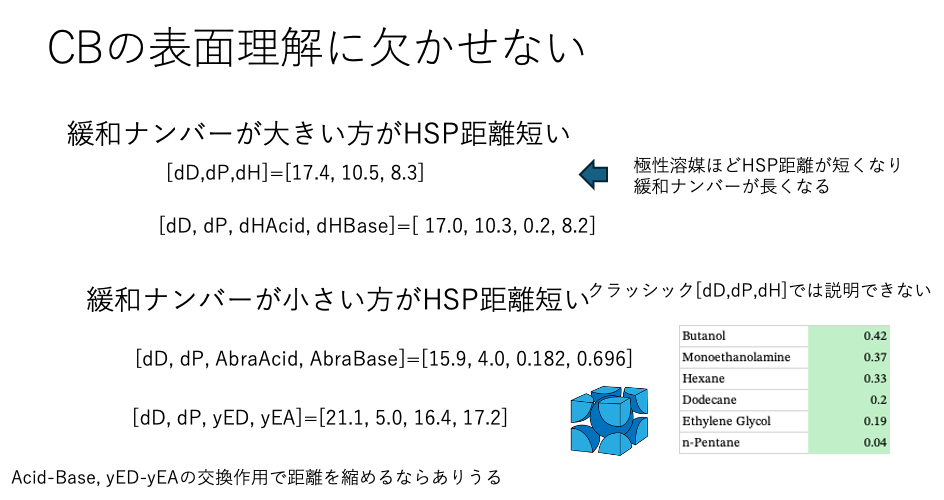
AbrahamのAcid/Baseか、Electron Donor/Acceptorの交換作用を入れないと緩和ナンバーの小さいものを正しく評価できない。
こうしたデータ駆動型の研究は、唯一無二の理論式を作るものではない。
Wrong In/Outが小さい方が良いモデルとも言えない。
一般的なHSPiPユーザーに提供しているアプリでもない。
この系に特化して何が起きているのかを考察するために行う。
MAGICIAN用の特別なツールである。
以上、Scoreは自分にとって好ましい溶媒に1をアサインするものではないことだけはよく覚えておこう。解析が逆になってしまう。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください)
メールの件名は[pirika]で始めてください
