Author: admin

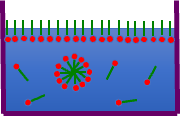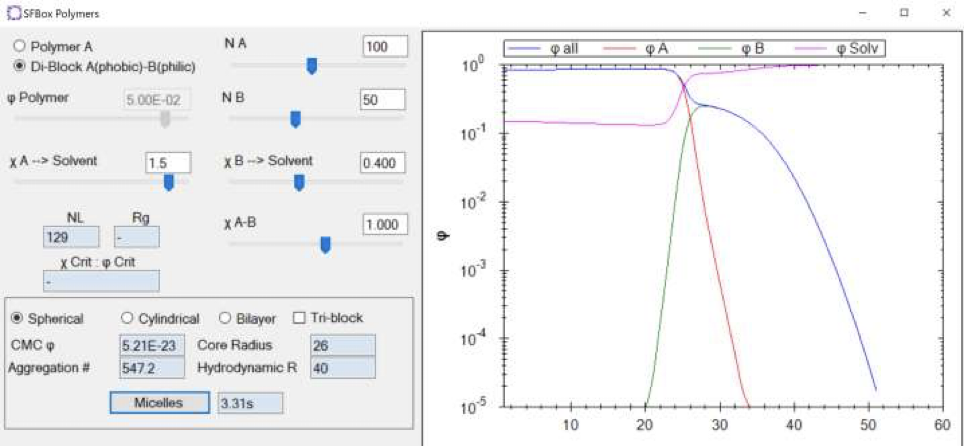
Using HSPiP’s SFBox, ” We can also get the calculated values of Critical Micelle Concentration (CMC), Aggregation #, Core Radius, and Hydrodynamic Radius”. I found this sentence in the e-Book.

SFBox is a feature introduced in HSPiP ver.5.3, I think. If you know CMC and Aggregation#, you can do a lot of things.
So, let’s summarize what we already know about surfactants.

But first, let’s remember the following formula.

So far, the textbooks will tell you.

First, let’s consider the Aggregation #.

For the volume of the hydrophobic group, for now, I will calculate the molecular volume using HSPiP’s Y-MB from the corresponding Smiles’ structural formula.

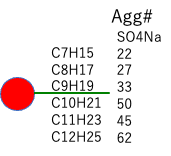
	Mol Volume	SO4Na-Agg#	Micelle-Volume	Micelle-radius	Micelle-Surface	Surface/Agg#
C6H13	120.0	17	2040.3	7.869	777.8	45.6
C7H15	136.7	22
C8H17	153.4	27
C9H19	169.2	33
C10H21	185.9	50
C11H23	202.6	45
C12H25	219.3	62

As the hydrophobic groups become larger, the Aggregation # also becomes larger. The micelle volume multiplied by the two will also increase.
The radius of the micelle will be easy to find.
Since (4/3)Πr3 is the molecular volume.
r=power(Vol*3/(4*3.14),(1/3))

The surface area of a sphere with radius r is 4Πr2, so if r is known, the surface area of the micelle can be calculated immediately.

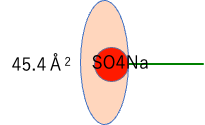
If we divide the surface area of the micelle by the Aggregation #, we can find the area covered by one hydrophilic group.

Now, let’s fill in the table.

What happens if we change the hydrophilic part?　The Aggregation # will look like the following table.

	Volume	COONa	COOK	COOCs	SO4Na	SO3Na	NH3Cl	NMe3Cl	NMe3Br	PyrBr	PyrCl
C7H15	136.7	20			22
C8H17	153.4				27	28			20
C9H19	169.2				33
C10H21	185.9				50	51			39
C11H23	202.6		50		45					42
C12H25	219.3		50		62	54	56	47	54	46	19
C13H27	235.1
C14H29	251.8					80	55	66	72	79
C15H31	268.5
C16H33	285.2				100			81	92
C12Ph	281.6					17
C6H13	120.0				17				3

Let’s find the hydration area of each hydrophilic group.

	水和面積
SO4Na	45.4
COOK
COONa
SO3Na
NH3Cl
NM23Cl
NMe3Br
Pyridine-Br
Pyridine-Cl	65.9
Phenyl-SO3Na	80.8

As you can easily see from the calculation, even if the structure of the hydrophilic group changes from SO4Na to Pyridine-Br, the hydration area is almost the same.
If the water molecules are arranged so that the hydration area is the same, there will be about 14 water molecules coordinated.

As an author of Y-MB in HSPiP, I am disappointed when people say “Y-MB cannot calculate HSP when salt is included like surfactant”. There is no problem at all if we use the same HSP as water for that part. At most, the value should be dependent on the hydration area.

And from the HSP of the hydrophobic area and the volume, we can calculate the HSP as the average value of the surfactant.
However, such an average value is completely meaningless, so I just don’t output it.

The interesting part here is the electron-donating and electron-accepting properties of water. That is what creates the hydration structure, not by the HSP.

Another very important point is that the salt (Phenyl-SO3Na) on aromatics has a very large hydration area. This is also true for the aromatic alcohol (phenol).

（It is very interesting to analyze polyoxyethylene:PEG surfactants in the same way. If there are many requests, I will make it public.)

So how much bound water is there in phenol?
This will be analyzed in the second half of the paper.

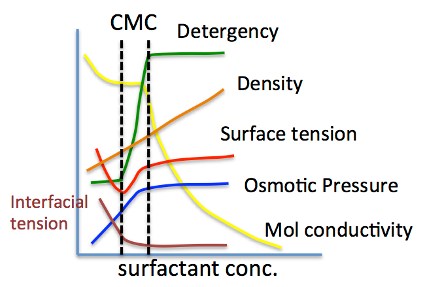
So, what is CMC (Critical Micelle Concentration)? Let’s think about it.

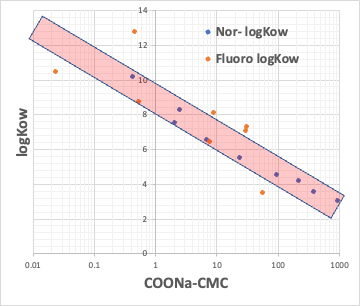
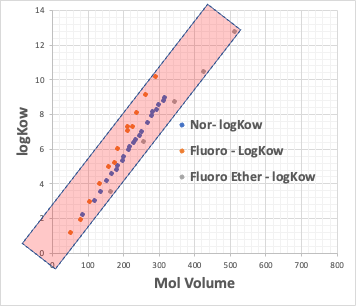
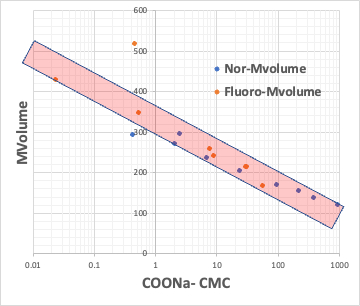
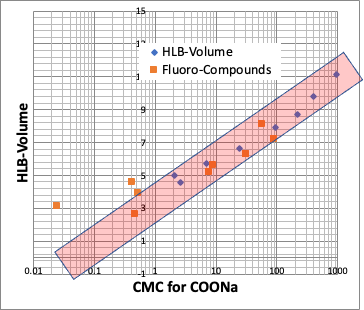
For example, plot the CMC of the Na salt of a carboxylic acid versus the logKow (octanol/water partition ratio) of the hydrophobic field of the carboxylic acid (the rest of the carboxylic acid with COONa removed).

The hydrophobic field can be a normal hydrocarbon or a fluorinated compound, but no matter which, there is an inverse correlation between CMC and logKow.

Small CMC means that micelles are formed at low concentrations. This happens when the molecular volume of the hydrophobic field is large.

This means that if the molecular volume of the hydrophobic field is determined, the CMC is determined and the Aggregation # is determined.
If the hydrophilic group is not an aromatic attribute, it doesn’t matter if the structure changes.

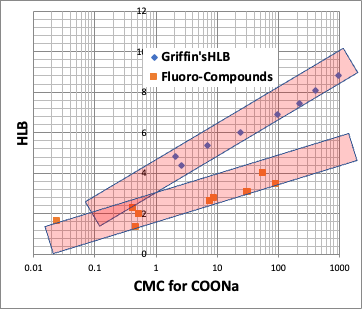
Incidentally, there is an evaluation value for surfactants called HLB (Hydrophile-Lipophile Balance). The most famous one is the Griffin method, which is calculated as follows.
HLB=20*sum of hydrophilic part formula/molecular weight
It is known that there is a high correlation between HLB and CMC.

Therefore, the HLB proposed by pirika is as follows.

pirika HLB = 20*sum of formula weight of hydrophilic part / molecular volume of hydrophobic part

In other words, HLB is also determined only by the molecular volume of hydrophobic field.

Thus, for surfactants, if we calculate the molecular volume of hydrophobic field using Y-MB in HSPiP, we can calculate CMC, Aggregation # and HLB.

I am very much looking forward to the consistency with SFBox.

Now, let’s consider hydrophobic interactions further.
Textbooks tell us that molecules with hydrophilic and hydrophobic moieties form micelles when the hydrophobic moieties come together through hydrophobic interactions.
However, looking at the data collection, it seems that micelles are not formed when the carbon chain is less than 6.
（It is said that when there are about 6 (unbranched) alkyl groups, the chains start to come together, and for many surfactants, hydrophobic interactions become more pronounced above C12.

How can we quantify that hydrophobic interaction?

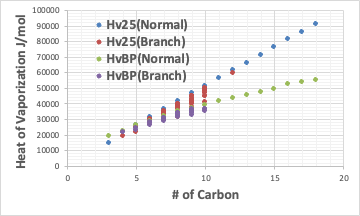
The latent heat of evaporation plotted against the carbon number of linear hydrocarbons looks like this.
The latent heat of evaporation at 25°C and the latent heat of evaporation at the boiling point are shown. Basically, the latent heat of evaporation at 25°C is greater than the latent heat of evaporation at the boiling point (unless the boiling point is below 25°C). That’s because it takes extra energy to heat it up from 25°C to the boiling point.
What is very interesting is that Hv25(Normal) is almost linear with carbon number.
HvBP(Normal) is a curve because the rate of increase in latent heat of evaporation decreases as the carbon number increases.

Also, the latent heat of evaporation becomes smaller as the number of branches increases and the molecule becomes more spherical, even for the same number of simplexes.

In such a case, it is useful to plot the latent heat of evaporation according to Trouton’s rule (plotting the latent heat of evaporation at the boiling point against the boiling point results in a straight line).

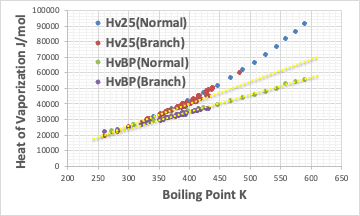
Thus, HvBP rides on a single straight line, whether it is linear or branched.
In contrast, Hv25 rides a straight line below C9, but above that, there is an obvious bend point. This is the extra energy needed to break down the hydrophobic interaction.
Since this is rarely the case for short alkyl chains, it is thought that micelles cannot be made.

Thus, we can understand the hydrophobic interaction to some extent, although originally we have to take into account not only the molecular volume of the hydrophobic field, but also the shape of the molecule (branching).

To be continued in the second half.