Author: admin

There are so many industries that can’t apply ordinal MI(Materials Informatics) to their job.
Here is one example listed in patent.

Beta column is Sensory Evaluation (feel very good=5, feel very bad=1). A, B, and C are the ingredients of the formula. Each ingredient is sold as a commercial product, and the exact contents are not known. You can imagine something like Carbon Black. CB(A-1) is bought from W-company, A-2 is from X, A-3 is from Y.

All we know is how much of each ingredient was used to create the formula and how many sensory evaluation values were obtained.
In fact, there are multiple types of sensory evaluation.

What we want to do is to use MI to design formulations that will result in multiple sensory evaluations, all of which will result in a 5-point rating.

But we can neither use the RDKit identifier nor the results of molecular orbital calculations for this case.
It is not easy to increase the data since hundreds of people are gathered for sensory evaluation.

What can MI researchers do about this problem?

If you are confident in your skills, create a prediction equation with the following data and try to predict the value of the predicted formulations.

Compound	Beta	A-1	A-2	A-3	A-4	A-5	A-6	A-7	B-1	B-2	B-3	B-4	B-5	C
E6	5	0	0	0	0	15	0	0	0	0	0	20	10	49
E12	5	0	0	0	12	0	0	4	30	0	0	0	0	49
E1	5	0	0	15	0	0	0	0	20	0	0	0	10	49
CE1	2	15	0	0	0	0	0	0	20	0	0	0	10	49
CE12	1	0	0	0	15	0	0	0	0	0	30	0	0	49
E4	5	0	0	15	0	0	0	0	0	0	0	20	10	49
CE8	2	14	0	0	1	0	0	0	30	0	0	0	0	49
CE5	4	0	15	0	0	0	0	0	0	0	0	20	10	49
CE10	4	0	0	0	15	0	0	0	60	0	0	0	0	19
E9	4	0	0	0	15	0	0	0	0.1	0	0	0	0	78.9
CE14	2	0	0	0	15	0	0	0	0	0	0	0	0	79
E8	5	0	0	0	25	0	0	0	30	0	0	0	0	39
E10	5	0	0	0	15	0	0	0	50	0	0	0	0	29
E11	5	0	0	0	9	0	0	6	30	0	0	0	0	49
CE11	2	0	0	0	15	0	0	0	0	30	0	0	0	49
CE13	2	0	0	0	15	0	0	0	0	0	0	0	30	49
CE6	2	0	0	0	0	0	15	0	0	0	0	20	10	49
CE2	4	0	15	0	0	0	0	0	20	0	0	0	10	49
CE9	5	0	0	0	30	0	0	0	30	0	0	0	0	34
CE7	2	0	0	0	15	0	0	0	0	0	0	0	10	69
E7	5	0	0	0	15	0	0	0	30	0	0	0	0	49
E5	5	0	0	0	15	0	0	0	0	0	0	20	10	49
Predict
CE4	2	15	0	0	0	0	0	0	0	0	0	20	10	49
E2	5	0	0	0	15	0	0	0	20	0	0	0	10	49
E13	5	0	0	0	14	0	0	2	30	0	0	0	0	49
E3	5	0	0	0	0	15	0	0	20	0	0	0	10	49
CE3	2	0	0	0	0	0	15	0	20	0	0	0	10	49

Pirika has new analytical tool, MIRAI(Multiple Index Regression for AI).

This time, I have made this tool into a web application.

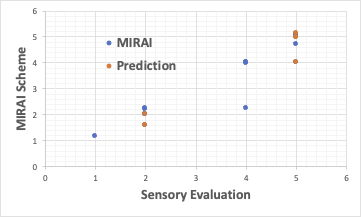
A typical multiple regression analysis would look like this.

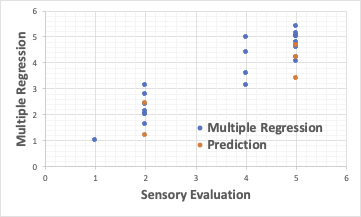
One disadvantage of the multiple regression method is that it cannot be used for those with interactions between explanatory variables or those that are nonlinear.

In contrast, MIRAI is a feed-forward type neural network method, designed to maintain predictive performance even with such a small number of data.

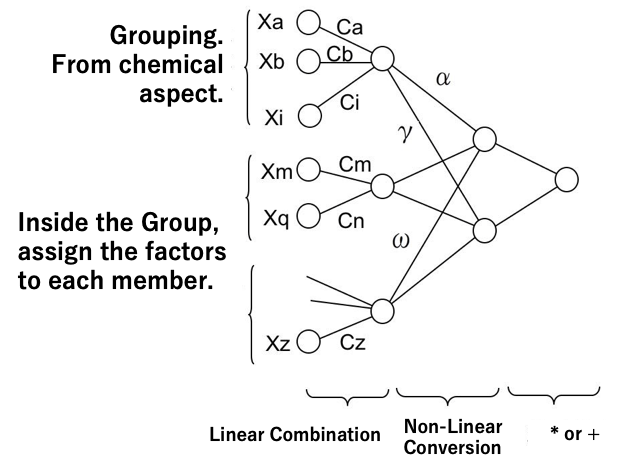
beta= C0 + Σ[(Ca*Xa+Cb*Xb・・Ci*Xi+1)^α
　　*(Cm*Xm+・・・ +Cq*Xq+1)^γ　
　　*(・・・　 　　+Cz*Xz+1)^ω ]

In this analysis, we have constructed an equation that reproduces the value of beta by multiplying the power function and estimate the results of the formulations that were not included in the training.

Once you have constructed the four different estimating formulas, you can then have the computer look for a formula that will give you an all-five rating.

I will put this MIRAI into GROVE.

Many examples are available at https://www.pirika.com/Education/JP/MAGICIAN/Examples/Formulation-Top.html