

| ホームページ | Pirikaで化学 | ブログ | 業務リスト | お問い合わせ |
| Pirikaで化学トップ | 情報化学+教育 | HSP | 化学全般 |
| 情報化学+教育トップ | 情報化学 | MAGICIAN | MOOC | プログラミング |
2012.1.12 (改訂2014.7.18)
フッ素樹脂ハンドブック(日刊工業新聞社) P.564に、フッ素ゴムが溶媒にどのくらい膨潤するかの一覧があります。
ポリマーを改良している研究者になったつもりで考えてみましょう。
このゴムは次のモノマーを共重合して合成されます。
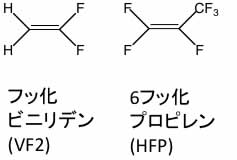
こうしたフッ素ゴムはパッキンなどのシール材に使われていますが、アルコール成分(ガソリンにエタノールを混ぜた混合燃料などで特に問題になる)で膨潤してしまう事が問題になっています。
次のデータをYMBを使って計算しておきましょう。 (Web版、学生版のYMBにはCNDO/2の計算結果は含まれていません。)
体積増加データ(表計算ソフトににペーストしておきましょう)
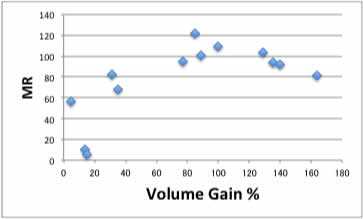
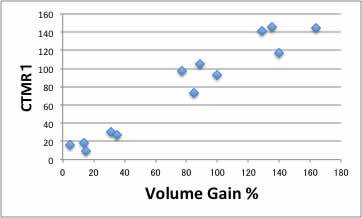
体積増加率と溶媒の物性値を比較してみましょう。
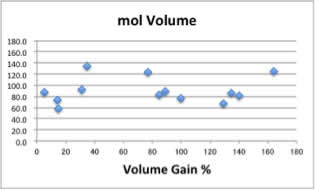
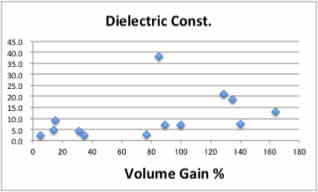
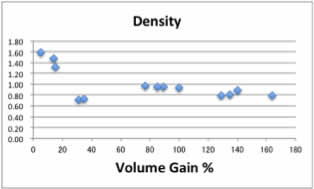
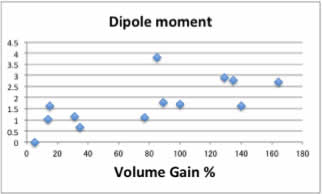
これらの図を見て、溶媒の物性のどれが、体積増加率にどう影響するか、定量的に答えられるでしょうか?
エタノールやETBだったら、どれだけ体積増加するか答えられるでしょうか?
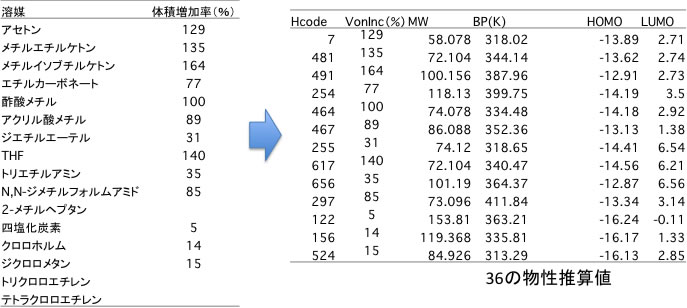
正しい分子のSmilesの構造式を与えれば、YMBは30個以上の物性推算値を出力します。
それをテーブルに入れ込んでおきましょう。
各溶媒の体積増加率と推算値の一覧テーブルを下のように作ります。
10分とかからないでしょう。
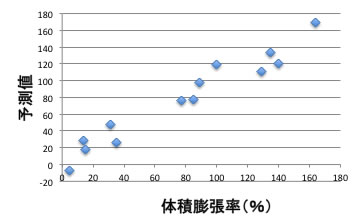
体積増加率と各物性との相関はグラフを一つずつ描いてみれば簡単に分かるでしょう。
それを行うには、まず表計算ソフトでグラフを描きます。
グラフを選択するとグラフで使われているカラムに色がつきます(X軸はピンク、Y軸は青。Macの場合)
その段階で下図のようにマウスでドラックするとカラムを入れ替えるとX軸はそのままに、Y軸のカラムを入れ替える事ができます。

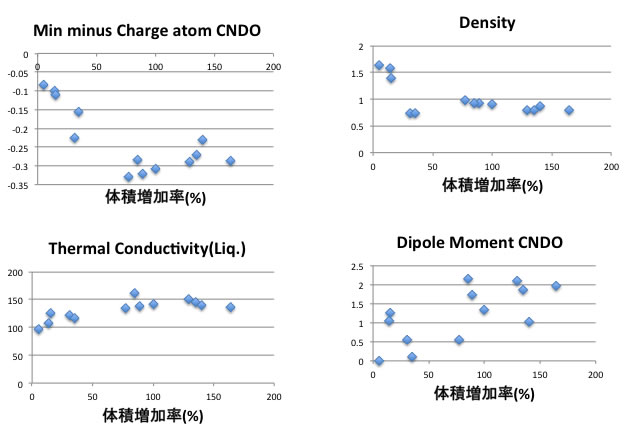
問題なのは、複数の物性が組合わさると、一つ一つの相関は低くても、悪い所がキャンセルされることもあるということです。
例えば、こんな式を作ってみます。
体積膨張率=-52.17*密度+30.31*ダイポールモーメント-181.1*負電荷最小値+52.63
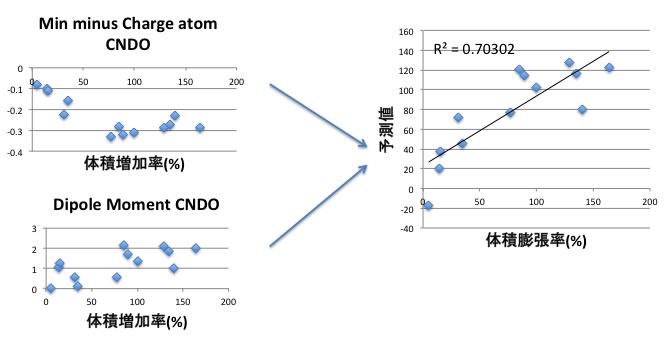
この場合の体積増加率のことを目的変数と呼びます。
そして溶媒物性の事を、説明変数と呼びます。
その間の関係を解析することを、重回帰分析と呼びます。
では、複数の説明変数のうち、どれを選んだらいいでしょうか?
36変数から3個の変数を取り出す、36C3=36*35*34/(3*2*1)=7140通り
36変数から4個の変数を取り出す、36C4=36*35*34*33/(4*3*2*1)=58905通り
これを手作業で行うのは大変な事は直ぐに分かるでしょう。
(エクセルのマクロも含め、コンピューターのプログラム言語を覚えるのは悪いことではありません。
もうしばらくすれば、情報化学でプログラミングを学んだ子供が育ってくるでしょうが。}
これを自動で行うのがYSBの中の変数選択重回帰機能です。
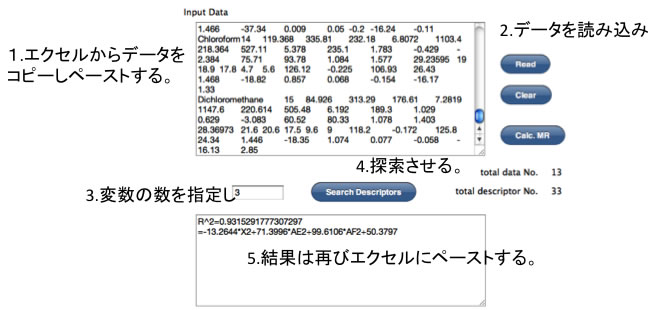
遺伝的アルゴリズムを使った方法なので、”必ずグローバルミニマムが見つかる”とは言えませんが、非常に高い確率でそれなりの相関係数を持った変数の組を見つけてくれます。
例えばこの体積膨張の例で変数4で探索すると、
体積膨張率=-16.08*log(HenryC) +0.66*Mol Volume +53.53*Dipole Moment -239.90*Min minus Charge -142.6891
を提案してくれます。
Henry定数は水へ溶解した時の蒸気圧の比例定数なので(Pirikaのこちらのページを参照)、水溶性の尺度となります。
それが効いていると思うか思わないかは化学者としてのセンスになります。
この推算式でエタノールを計算すると、体積膨張率の推算値は78%になります。
このようにして、このポリマーは、分子中の負電荷が大きい原子を持ち、ダイポールモーメントが大きい溶媒に良く膨潤することが分かります。
それは何故でしょうか?
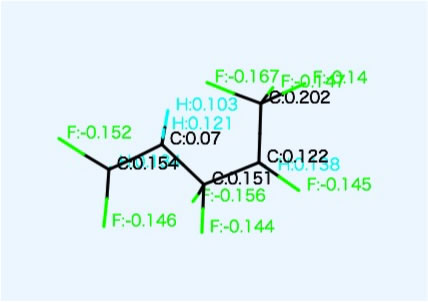
学生版のYMBを使うと各原子上の電荷を計算する事ができます。
(チャージ計算はPirikaのこちらの資料を参照)
それを見ると、このポリマーは水素の電荷が+、フッ素の電荷がーにチャージされ大きなダイポールモーメントを持つ事がわかります。
そこで、溶媒が分子中に大きな負電荷を持つと、それはおそらく水素の部分に配位して溶媒和するのでしょう。
最新のマテリアルズ ・インフォマティクス では、説明変数が多くなったときには、主成分解析やPLS法を使いましょうと教えてくれます。
主成分解析はPirikaのこちらのページを参照してください。
PLS法はPirikaのこちらのページを参照してください。
それなのに、何故あえてそれを使わないのでしょうか?
高い相関関係を得るのが目的なら、PLS法で良いのでしょう。
しかし、このゴムの膨潤性の本質を知るのが目的であるなら、地道に何故かを考える癖をつけておいた方が、後々研究の役に立つからです。
所詮、ビッグデータは集まりません。
少ないデータから正しくポリマーの改良方向を知るためには、本質をよく見るのが早道な事が多いです。
そこに、AIと人間の研究者の違いを見せつけるようにしていかないと、存在意義が失われて行きます。
実際の改良としては、よりフッ素含量の多いポリマー(F-73%)が合成されました。
ちなみに元のポリマーはF-70%です。
高フッ素含量データ
課題: 改良後のポリマーがエタノールでどのくらい体積増加するか検討してみましょう。
2014年改訂
ハンセンの溶解度パラメータ(HSP)を用いてやってみましょう。
このような推算式を作る際に一番大事なのは、系列の異なる予測式を何種類か作成することです。
まずは自動的に選択させてみる。
使う変数の数を変え、いつも選ばれる変数を特定する。
関連しそうな同族パラメータだけから推算式を作成する。
例えば、
HSPと分子体積
臨界定数+α
logKow+logS+分子体積
など色々考えてみます。
それではHSPを使ったやり方を説明しましょう。
Smilesの構造からYMBで計算した値を使います。次のように表を埋めましょう。
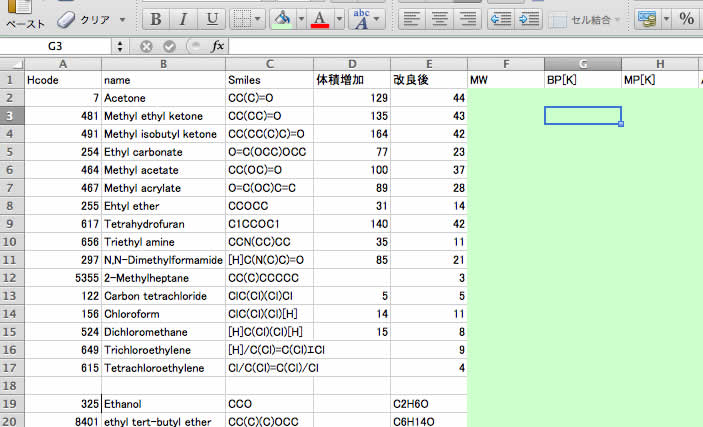
そして、YMBの計算結果のうち、ハンセンの溶解度パラメータの部分を埋めてYSB用のセットを作ります。(一部の分子で体積増加の値が無いものがあるので注意してください)
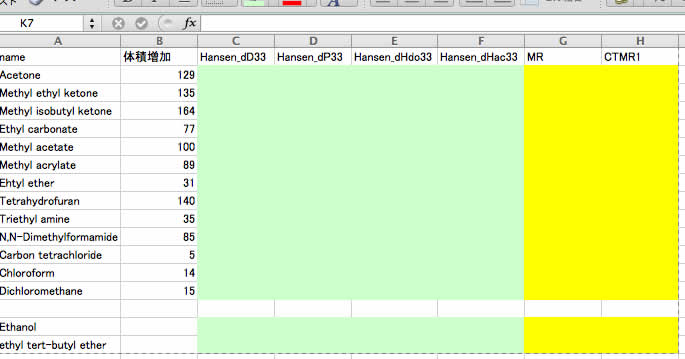
そしてYSBで重回帰計算を行います。
重回帰の結果
クロスタームを1つ入れた場合の結果
クロスタームの意味が分からなければ、重回帰の基礎を読み直しましょう。
課題
選択されたクロスタームは何にな利ましたか?
何故そのクロスタームが選ばれたと思いますか?
エタノールの体積増加は幾つになると予測されましたか?
これは妥当であると思いますか?
日本ではETBE(ethyl tert-butyl ether)が使われるとして、体積増加は幾つになりましたか?
このフッ素ゴムはフッ素含量をアップする事によって耐溶剤性の改良が検討されました。
改良後の体積増加率の推算式をHSPを使って求めてください。
その時のエタノールとETBEの体積増加率を求めてください。
このように、最先端材料であるフッ素ゴムの耐溶剤性が、ハンセンの溶解度パラメータで見積もる事ができるようになります。
こうしたフッ素ゴムのフッ素含量を上げる為には、次のようなパーフルオロのモノマーをVF2, HFPと共重合します。(パーフルオロ・モノマーが入った分だけフッ素含量がアップします。)
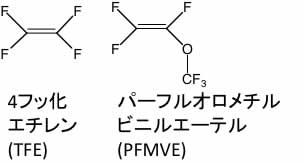
ここでは、TFEを使うとして、VF2, HFPとの3元系のポリマーを考えてみましょう。
こうしたフッ素ポリマーをゴムとして扱う上で重要なのはゴムの耐寒性です。
ゴムは冷やされる事で弾性を失います。
それを回避する為にはポリマーのガラス転移温度(Tg)が重要になります。
フッ素樹脂ハンドブック(日刊工業新聞社)にこの3元系のポリマーのTg点が記載されています。
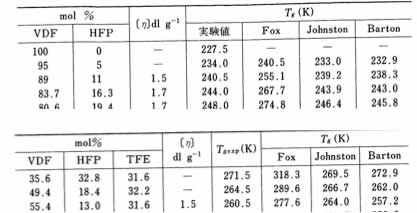
ガラス転移温度データ
課題:
YSBを使ってTg点の推算式を構築してください。
Tg = XXX*VDF(mol%) + YYY*HFP(mol%) +ZZZ*TFE(mol%) +const.
グラフは次のようになりましたか?
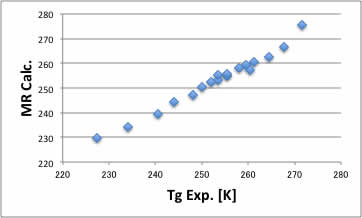
この式とグラフの意味する事は何か考えてみてください。
ただし、3元系でフッ素含量が73%であればどんなポリマーでも良いという訳ではありません。
"Technology of Fluoropolymers", Jiri George Drobny, CRC Pressには次のような三角図が載っています。
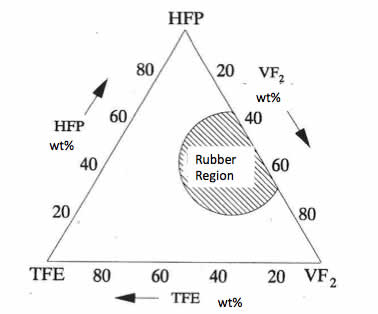
この3角図の意味する事は、この3元系のポリマーではゴム領域となるポリマー中の組成は斜線の所に限られる、という事です。
フッ素含量が73%と決まっているのであれば、VDF(100-x-y)、HFP(y)、TFE(x)としたときに
2*(100-x-y) : 2*(100-x-y)+6y+4x= 27:73
という方程式が成立します。
変数が2つで、式が1つなので解けません。
そこでゴム領域となる条件
VdF 30-70% 100-(x+y)
HFP 20-60% y
TFE 0-40% x
から、xの量を1-40まで1%刻みで仮定してみます。
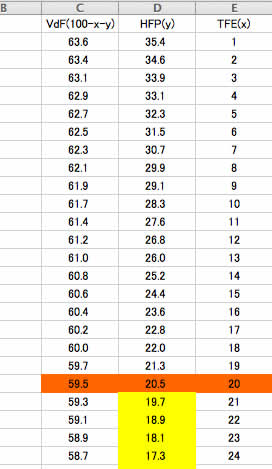
すると、VDFの量とHFPの量は一つに決まります。
そして、TFEの量が20%を超えるとHFPの量がゴム領域を外れる事がわかります。
(実際にはゴム領域のデータはwt%でTgの推算はmol%なので正しくはありませんが。)
それにしてもTFEを細かく取ればフッ素含量が73%の処方は無数に存在する事が判るでしょう。
課題:
先に求めたTg点の推算式を使い、ゴム領域を満足するポリマー組成のうち最も低いTgとなる組成をテーブルから選んでみましょう。
こうして、Tg点を一番低くするフッ素含量73%のポリマー組成が求まったとしても、モノマーをどの比率で仕込めばそうしたポリマーができるかは別問題です。
それはモノマーの反応性比によってポリマー中に導入されるモノマーの比は仕込みの比とは異なるからです。
それについてはポリマーのシーケンス解析で別途説明します。
同様なポリマーの膨潤性に関しては、LiB用のバインダーポリマーがあり、同じようにHSPを使って解析がなされています。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。