自然哲学から自然科学へ変わった1600年代、天文学、電磁気学、物理学は観測されるデータを分析し、論理・法則を見出して行く手法が確立された。しかし化学は取り残された。観測するためのツール、温度計が無かったからだ。
そこで、未だに「測定は室温」とか言う曖昧な言葉がまかり通る。
密度、粘度、表面張力、比熱、熱伝導度などは温度が変われば物性値が変わるのにだ。
例えば、ある薬の膜透過係数を考えてみよう。防御用の手袋でも良い。HSPiPのe-Bookを翻訳していた時次のような表現があった。
A rigid molecule or a highly branched molecule takes much longer to find a space or “free volume” in which to wiggle.
剛直な分子や枝分かれの多い分子は”くねくね進むための”空間、自由体積を見つけるのに長い時間がかかる(ので、破過時間が長くなる)。
つまり、大きさ、形状、温度、分子間力(例えば水素結合)によってクネクネ状態は変わるのに、温度は実験の際には室温共通なので考察に入ってこない。
pirikaでは温度を換算温度で考える。
(反応速度を1/Tでプロットする、アーレニウス・プロットに近い。)
そこで、温度を次式で換算する。
Temp.pirika=Antoine B/(Antoine C + Temperature[℃])
ここで、Antoine定数(A, B, C)は、蒸気圧をAntoine式で計算するときの定数になる。
Antoine Equation: log P(mmHg)=Antoine A – Antoine B/(Antoine C + Temperature[℃])
Antoine定数は化合物ごとの定数で、その推算方法は別のBlogで述べるが、その方法はHSPiPのY-MBに搭載されている。
つまり、液体分子が衝突して、液相から気相に飛び出る温度効果を同じにしてあげる。
膜の透過は分子が大きいほど、剛直なほど、環状であるほど、分子間力が大きいほど小さくなる。
同じように、粘度はそのような化合物であるほど高くなる。
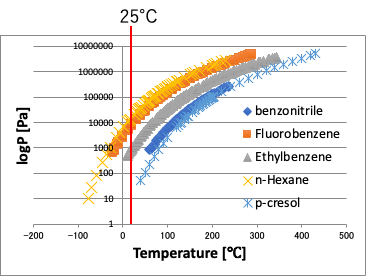
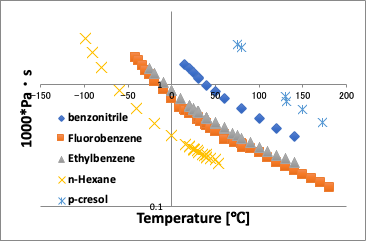
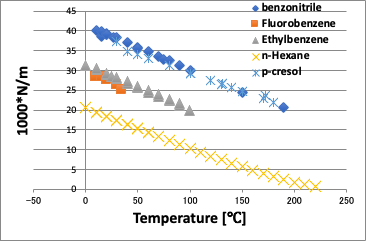
通常の温度に対してプロットすると上の左の図のように温度が高くなるにつれ粘度が下がる曲線が得られる。
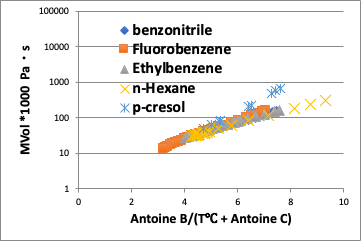
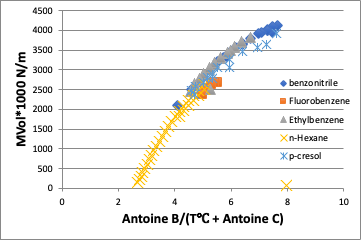
それに対して、換算温度に対してプロット(この場合、分子体積がキャンセルできないので縦軸は粘度*分子体積にしてある)すると分子の違いは吸収され、曲線はほぼ直線になる。
ここで非常に興味深いのは、p-Cresolは70℃以下の低温では直線から乖離してくる。
これは水素結合の特徴で、温度が低いところでは強い水素結合があることが推察される。
Antoine Bは蒸発潜熱と相関があるので、分子が大きくなれば大きくなる。
Antoine Cは極性と相関があるので、水素結合などが大きくなると小さくなる。
従って、変換温度は、分子の大きさや極性まで含めたパラメータになる。
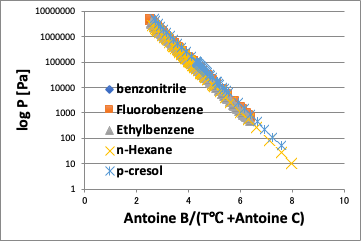
表面張力も換算温度で取ると分子の差はほとんど無くなる。
それでは、ニトリル手袋の破過時間(BTT)を考えてみよう。データは次のサイトから収集した。
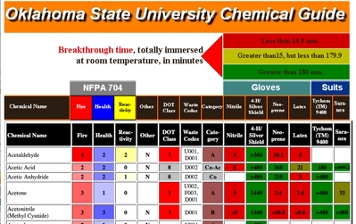
どんな化合物が破過時間が短くなるのかを調べるために、HSPを3次元にプロットしてみる。
赤色はBTTが10分以下、オレンジが50分以下、黄色が150分以下、150分以上は青色にしてある。
Z(水素結合項)が大きいものはBTTが大きくなる傾向があるが、赤色はハンセン空間に広く散らばり、HSPの値によってBTTが大きくなったり、小さくなったりするようには見えない。
これは、BTTには分子の大きさなども関与するからだと考えられる。
そこでHSPに体積を加えて表示させたい。その時には、こちらで説明したようにPCA(主成分解析)を行って、多次元を3次元に縮退させる。
すると、3次元の空間を貫くほとんど一本の線になる。赤が多く集まった端は分子体積が小さく、逆の端は分子体積が大きい。
それに対して、HSPに換算温度を加えてPCA解析すると、とても興味深い分布になる。これが溶解性に加え、くねくね度を加味したBTTのビジュアライゼーションになる。
さらに、水素結合項を分割したり、E D,EAを導入したりして、BTTの解釈を豊かにすることができる。
薬剤の皮膚への浸透なども、このようにくねくね度を導入して考える必要があるのだろう。