MIRAIによるMI（マテリアル・インテグレーション）研究

普通のMI(Materials Informatics)を仕事に活かせない業界は非常に多いようです。
ここでは、特許に記載されている一例を紹介します。

Beta欄は官能評価（とても良いと感じる＝5、とても悪いと感じる＝1）結果です。A,B,Cは、配合成分です。それぞれの成分は市販品として販売されており、正確な内容はわかりません。カーボンブラックのようなものを想像してください。CB(A-1)はW社から、A-2はX社から、A-3はY社から購入しています、などです。

分かっているのは、それぞれの成分をどれだけ使って配合したか、官能評価値がいくつ得られたかだけです。
さらに、官能評価には複数の種類があります。

私たちがやりたいのは、MIを使って、複数の官能評価値の予測値が得られ、すべての評価値が5点になるような処方を設計することです。

しかし、この場合、RDKitの識別子も分子軌道計算の結果も使えません。
また、官能評価には何百人もの人のデータを集めるため、データを増やすことも容易ではありません。

この問題に対して、MIの研究者はどうすればいいのでしょうか？

腕に自信のある人は、次のデータで予測式を作り、予測処方の値を予測してみてください。

Compound	Beta	A-1	A-2	A-3	A-4	A-5	A-6	A-7	B-1	B-2	B-3	B-4	B-5	C
E6	5	0	0	0	0	15	0	0	0	0	0	20	10	49
E12	5	0	0	0	12	0	0	4	30	0	0	0	0	49
E1	5	0	0	15	0	0	0	0	20	0	0	0	10	49
CE1	2	15	0	0	0	0	0	0	20	0	0	0	10	49
CE12	1	0	0	0	15	0	0	0	0	0	30	0	0	49
E4	5	0	0	15	0	0	0	0	0	0	0	20	10	49
CE8	2	14	0	0	1	0	0	0	30	0	0	0	0	49
CE5	4	0	15	0	0	0	0	0	0	0	0	20	10	49
CE10	4	0	0	0	15	0	0	0	60	0	0	0	0	19
E9	4	0	0	0	15	0	0	0	0.1	0	0	0	0	78.9
CE14	2	0	0	0	15	0	0	0	0	0	0	0	0	79
E8	5	0	0	0	25	0	0	0	30	0	0	0	0	39
E10	5	0	0	0	15	0	0	0	50	0	0	0	0	29
E11	5	0	0	0	9	0	0	6	30	0	0	0	0	49
CE11	2	0	0	0	15	0	0	0	0	30	0	0	0	49
CE13	2	0	0	0	15	0	0	0	0	0	0	0	30	49
CE6	2	0	0	0	0	0	15	0	0	0	0	20	10	49
CE2	4	0	15	0	0	0	0	0	20	0	0	0	10	49
CE9	5	0	0	0	30	0	0	0	30	0	0	0	0	34
CE7	2	0	0	0	15	0	0	0	0	0	0	0	10	69
E7	5	0	0	0	15	0	0	0	30	0	0	0	0	49
E5	5	0	0	0	15	0	0	0	0	0	0	20	10	49
Predict
CE4	2	15	0	0	0	0	0	0	0	0	0	20	10	49
E2	5	0	0	0	15	0	0	0	20	0	0	0	10	49
E13	5	0	0	0	14	0	0	2	30	0	0	0	0	49
E3	5	0	0	0	0	15	0	0	20	0	0	0	10	49
CE3	2	0	0	0	0	0	15	0	20	0	0	0	10	49

Pirikaには新しい分析ツール、MIRAI(Multiple Index Regression for AI)があります。

今回、このツールをWebアプリ化しました。

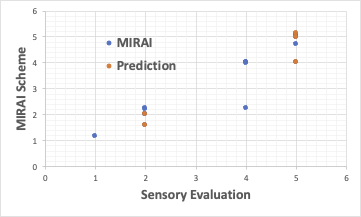
通常の重回帰解析では、次のようになります。

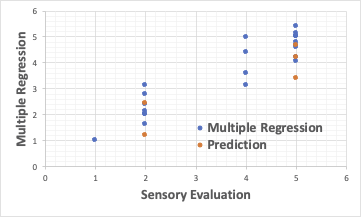
重回帰法の欠点として、説明変数間に相互作用があるもの、非線形なものには使えないことが挙げられます。

それに対して、MIRAIはフィードフォワード型のニューラル・ネットワーク法で、データ数がこのように少なくても、予測性能を維持できるように設計されています。

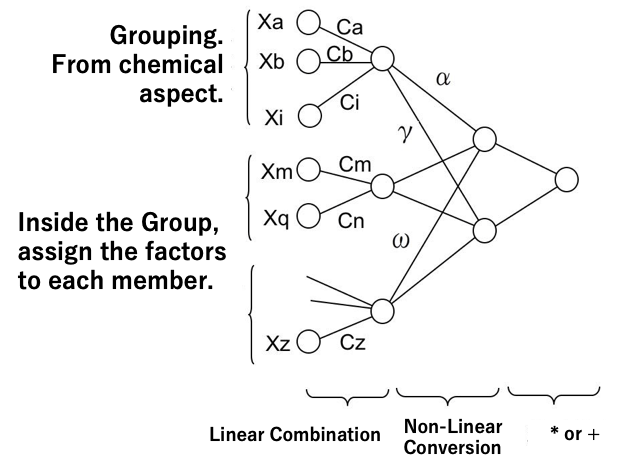
beta= C0 + Σ[(Ca*Xa+Cb*Xb・・Ci*Xi+1)^α
　　*(Cm*Xm+・・・ +Cq*Xq+1)^γ　
　　*(・・・　 　　+Cz*Xz+1)^ω ]

今回の解析では、パワー関数の掛け算でベータの値を再現する式を構築し、学習に含めなかった処方の結果を推算しています。

４種類の推算式を構築してしまえば、後はコンピュータ上で片っ端に評価がオール５になる処方を探させれば良いのです。

I will put this MIRAI into GROVE.

塗料、インク、化粧品の特許への応用例をこちらにまとめました。