夢の中でだ。
機械学習に関する初歩的なことを書いている。
解説しにくいことを悩んでいる。気分を変えようと「科捜研の女」を見てから寝たので夢に出てきたのかもしれない。
まりこさんは電話会議でメンバーを招集して相談にのってくれたが、他の人はボソボソ言っているだけで何を言われたのか判然としない。
ことは、機械学習の基本、重回帰法だ。

果物の詰め合わせが売っています。
この連立方程式を解いて、各果物の値段を求めてください。
小学生でも筆算で解ける子はいるだろう。
これは、機械学習の一番シンプルな例題だけど、とても誤解を生む。
解いた答えが各果物の値段なので、重回帰法の答えは(多少の誤差はあるとしても)一つに求まると勘違いしてしまう。
そして、値段(係数)の大きい果物(成分)を増やせば、トータルの値段(例えば薬の活性)は高くなると勘違いしてしまう。

次の場合はどうだろうか?
バーガーが4種類、ポテトが4種類、飲み物が5種類あって、各グループの中から1つを選んでセットを作る。その3つの値段がpriceになる。各バーガーとポテト、ドリンクの値段を求めなさい。
| No | Price | Burger1 | Burger2 | Burger3 | Burger4 | Potato1 | Potato2 | Potato3 | Potato4 | Drink1 | Drink2 | Drink3 | Drink4 | Drink5 |
| 1 | 145 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 165 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 111 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 130 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 77 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 6 | 114 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 7 | 60 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 8 | 132 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 9 | 175 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 10 | 121 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 11 | 111 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 12 | 95 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 13 | 130 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 14 | 77 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 15 | 77 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 16 | 60 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 17 | 96 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 18 | 95 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 19 | 114 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 20 | 60 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 21 | 132 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 22 | 150 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 23 | 199 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 24 | 145 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 25 | 165 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 26 | 111 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 27 | 183 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
変数が13個で式が27個あるので、連立方程式を解けばよい。Excelにデータをコピーして、分析(必要に応じてAdd-inをインストールしなければならないが)/回帰計算を行えば良い。
Excelを持っているならやってみよう。
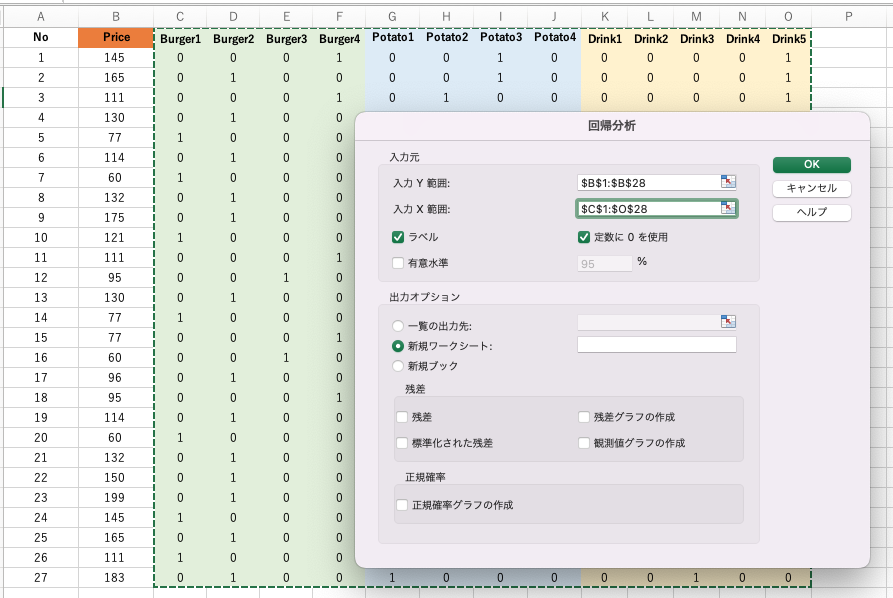
すると、重相関係数 R=1で、各値段がわかる。
| Burger1 | Burger2 | Burger3 | Burger4 | Potato1 | Potato2 | Potato3 | Potato4 | Drink1 | Drink2 | Drink3 | Drink4 | Drink5 |
| -17.99 | 35.98 | 0.00 | 16.45 | -60.91 | -78.90 | -44.45 | 0.00 | 174.95 | 138.97 | 207.86 | 156.96 | 173.41 |
困ったことに、値段が0円とかマイナスのものが現れてしまう。
でも、16.45*burger4 + -44.45*Potate3 + 173.41*Drink5 =145になるので式はどれも正しい。
ものの値段なので0円とかマイナスは嫌なので、係数を0以上という制限をつけて計算してみる。(手頃なソフトが見つからなかったので、自作のソフトで探索してみる。)
係数は次のように求まる。
| Burger1 | Burger2 | Burger3 | Burger4 | Potato1 | Potato2 | Potato3 | Potato4 | Drink1 | Drink2 | Drink3 | Drink4 | Drink5 |
| 20.71 | 74.71 | 38.76 | 55.68 | 32.72 | 14.72 | 48.72 | 93.69 | 42.57 | 6.60 | 75.57 | 24.57 | 40.60 |
この2種類の係数をプロットしてみると全く異なる系列であることがわかる。ExcelではDrink類が高価だったが、そうでもない。
同じバーガーだけで見ても、この値段はExcelでは4>3>1>2であるが、私のソフトでは、2>4>3>1になる。
つまり、解の精度がほぼ同じような係数の組みは幾つでも見つかることになる。
こうした重回帰法の問題点を見ると、統計をよく知っている人は、多重共線性の問題があるのではないかと言う。
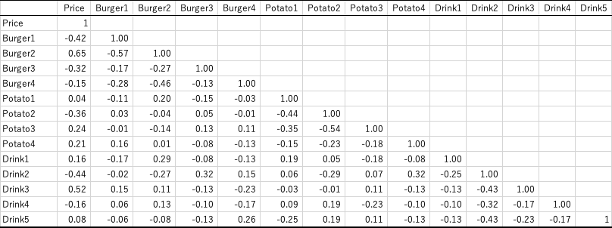
Excelで相関を取っても、問題がないことがわかる。
実を明かせば、このテーブルはハロゲン置換のプロピレンタイプの化合物を表している。値段は分子量(MW:Molecular weight)だ。
| MW | CH3 | CF3 | CH2F | CH2Cl | CF= | CH= | CCl= | CBr= | CF2= | CH2= | CCl2= | CHF= | CHCl= |
| Price | Burger1 | Burger2 | Burger3 | Burger4 | Potato1 | Potato2 | Potato3 | Potato4 | Drink1 | Drink2 | Drink3 | Drink4 | Drink5 |
化学系では当たり前だが、CX3CY=CZ2という骨格のX,Y,ZにH, F, Cl, Brなどがくる。
であるから、CH2FはCF=より水素2つ分、分子量が増えなくてはならない。
周期律表から原子の重さを持ってくれば、CH3の係数は、12+1*3で15.xxxと厳密に決まるし、相関係数は1.0になる分子量計算式が得られる。
どの計算式を使っても、分子が決まればほぼ同じ分子量が計算される。
だが、どの原子団が増えたら結果をどう変えるかの尺度は与えない。
単品値段(係数)の大きい果物、バーガ成分(成分)を増やせば、トータルの値段(例えば薬の活性)は高くなる。
これが成り立たない事がある。
多重共線性ではない。
リッジ回帰でもLASSO回帰でも、主成分分析(PCA)でもPLSでもなんでも良い。
情報化学の総力を上げて、一番悪さをするやつから最低限、序列ぐらいは正しくなる係数を求める方法を教えてほしい。
また、多重共線性のように、「説明変数間に0.9以上の相関がある場合には気をつけな」というようなガイディング・プリンシプルが欲しい。
「科学の力で真実を解明する」まりこさんに、夢の中でお願いしたことだ。。。
何故、係数の値が不定になるのかは、教えてくれた。
小学生と同じように変数消去してみれば良い。
CF3-CH3=54
CF3-CH2F=36
CF3-CH2Cl=19.5
が成立するだけだ。
CF3がどんな値を取ろうとも、それに合わせたCH3, CH2F, CH2Clが決まるのでグループ内では不定になる。
大学での研究のように対象が限定されず幅広い時にはこの問題が出てくることは少ないが、系を絞って最後のスクリーニングのような企業の研究では思わぬ落とし穴になりうる。MIに行き詰まったらドラマでも見て気晴らししよう。
まー、大学生時代に(結婚物語に出てた)沢口靖子が大好きだった自分からすれば、よき「真夏の夜の夢」と言えようか。
そんな事思っていたら、大学生の息子も沢口靖子は美人だとか言い出して、男どもで盛り上がっている。
