データの見えざる手。矢野和男。を読み始めた。
30*30のマス目に30*30*100個のボールをランダムに投げ込む。
当たり前のことだけど、一つのマス目には平均100個のボールが入る。
平均よりも少ないこともあるし、多いこともある。しかし、分布はいわゆる左右対称の正規分布になる。
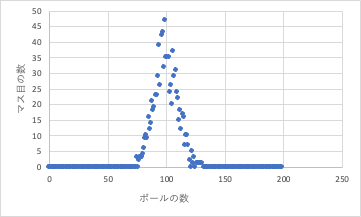
プログラムを書いてコンピュータで試したところ、このようになった。
一番少ないもので、75個、一番多いもので、131個入ったマス目があった。ここまでは、普通の統計の話で議論の余地はない。
問題は、出来上がったこの分布のものを、ランダムに一つのマス目を選びボールを一つ取り出し、ランダムにマス目を選び1つを選びボールを加えるという操作を繰り返した時にどうなるか?だ。
いっぱい入っているマス目から取り出されたり、少ないものから取り出されたり、多いものにそれが加えられたり、少ないものに加えられたりする。
それがランダムで十分大きな回数繰り返せば、元の分布状態と変わらない。とほとんどの科学者が考えたという。私もそう考えたし、著者の説明に納得がいかなかったので、実際にプログラムを作って試してみた。
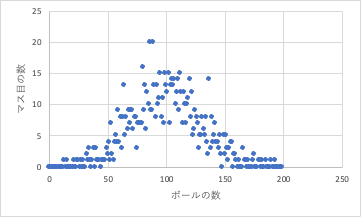
30*30*400回、ランダムに動かすと,平均は100個のままだけど、分布は確かに非常に広がった。
本の筆者は、ランダムな交換なのに、多くのボールを持つマス目がさらに多くなり、少ないところは更に少なくなっている。これが等価交換をしていても富が偏在化する原動力であると言っている。
富むものがますます富むのは、エントロピー(乱雑さ)増大の法則に反している。人間など、統計的でない生き物の行動ならともかく、ランダムに動かすならエントロピー増大の物理法則は守ってくれないと困る。
プログラムを作って色々動かしてみると、だんだん色々なことがわかってきた。
私の得たのは、この結論から「富めるものがますます富む」というのは間違いだ。
さー、データ・サイエンティストやら、統計解析の専門家は、この問題に何て答えるだろうか?
少なくとも、モンテカルロや遺伝的アルゴリズム法を多用する私としては、ランダムという概念を見直す必要はあるかもしれない。
