2021.5.5
情報化学+教育 > 情報化学 > 解析用のツール、GROVE

世界相手に戦うぜ!
|
学生が開発してきた、解析ツールがいい味を出してきました。 養成講座に参加している方と名前を考えて”GROVE”という名前にしました。 |
GROVE Gene-based Regression Offering Valuable Equations.
貴重な式を提供する遺伝子ベースの回帰分析
化学系のデータには様々な理由で汚いデータが混じってきます。
それを誤差逆伝播させてしまうと、例え、それがニューラルネットワーク法であろうと重回帰法であったとしても係数を大きく悪くしてしまいます。
そこで
誤差 =(質の悪い)教師データ ー 計算値
と誤差を定義してしまうと、誤差が大きいのは、計算値が悪かったのか、教師データの質が悪すぎたのかは、どこまで行ってもわかりません。
そこで係数の決定に誤差を逆伝播させない、フィードフォワード法を採用することにします。
また、解析的に式を解いてしまうと(逆行列法)どうしても誤差の影響を受けてしまうので、ヒューリスティクス(Heuristics:発見的)方法の遺伝的アルゴリズム法(GA: Genetic Algorithm)を採用しました。
私の基本的方針:「学生は死なない程度の失敗をやり尽くしてから社会に出るべき」と言うのがあります。
私は、ほとんどテーマごとに最適な解析ツールを自作してからテーマを行うことを、会社で25年間繰り返してきました。その経験は学生に簡単にトランスファーできるものではありません。
「こういう問題があるけど、この問題を解決できるツールはどうしたら開発できる?」
そうした問いに対して、「こんなふうに機能を実装しました。」と徹夜でプログラムを作成して提出してくれます。
「ダメー」この結果はアクセプトできない。1週間時間をあげるけど、1週間で解決できないのなら、答えを言ってしまうからね。
学生の作ったプログラム。ソースコードは見ずに、いくつか試しに走らせ、動作の特徴をつかみ、この系を解析したらこのような解析結果を得ました。どうしたらそのような結果を得られるのか、他のMAGICIAN養成講座に参加している研究者に説明してください。
「どうにも、じゃじゃ馬で、自分で作っておいて、自分では乗りこなせていません。」
「どうやってもそのような結果は得られません。」
「悔しくてしょうがありません」
そうした経験をたくさんさせてから社会に送り出そうと日々楽しんでいます。
ちょこちょこっと、Pythonだかを学んであやめの分類やって社会人になるデータ・サイエンティストとは違うぞって言える、解析ツールGROVEの開発の話です。
データ・クレンジングの問題
まず初めは、データ・クレンジングの問題です。
ここにあるデータがあります。適当に作った問題なので適当に読み替えてもらっても結構です。
課題は、
あるデータに対して、適当に誤差を与えました。
どのデータに誤差を幾つ与えたかを特定してください。
と言うものです。
イメージがわかないでしょうから、具体例で説明しましょう。
ある有機化合物の沸点はJOBACKの沸点推算式で計算できます。
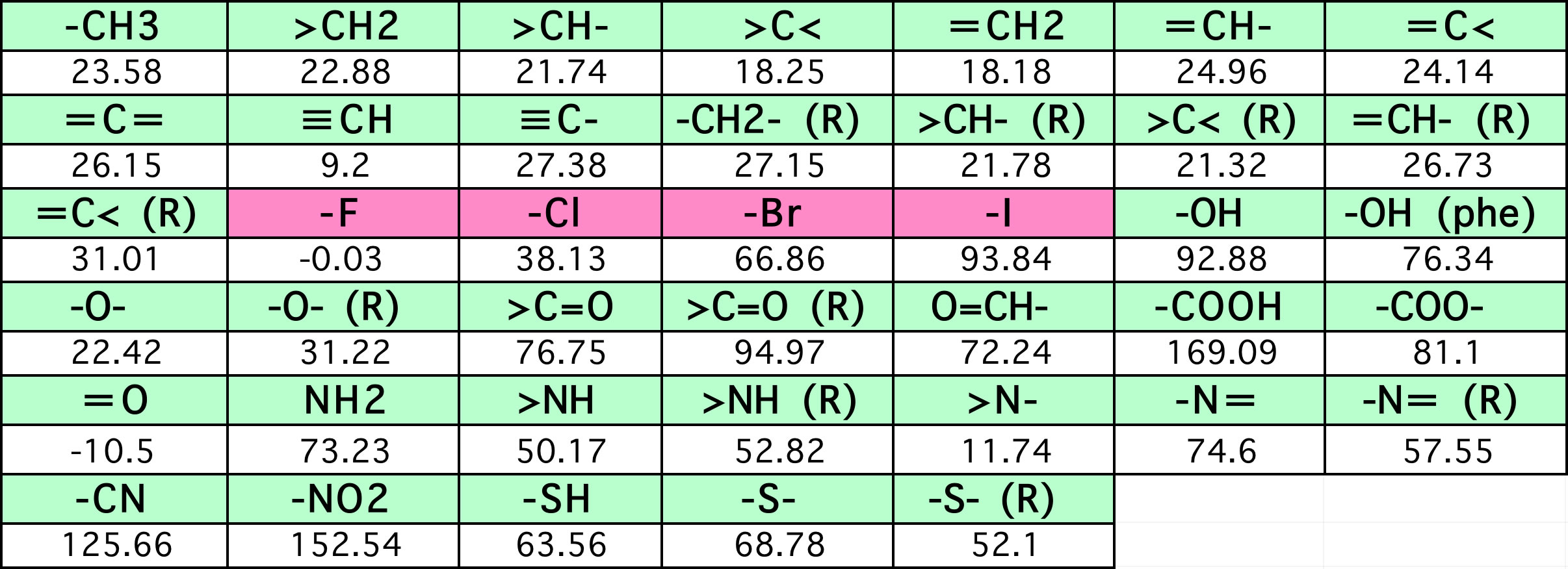
沸点=198.2+Σ(原子団の数 * 表中の係数)
つまり、分子構造が与えられれば、その沸点のJOBACK計算値は簡単に得ることができます。
色々な化合物についてJOBACK法の沸点計算値のテーブルを作成します。
そのテーブルを使って重回帰計算を行えば、各原子団の重回帰係数は簡単に得ることができます。
元のJOBACKの係数は簡単に再現できます。
それでは、恣意的に、テーブルの中の30分子を乱数で選んで、さらに乱数(0.0-1.0)に60℃掛けた値を足したテーブルを作りました。テーブルの中には161個の化合物があるので、18.6%の化合物に平均30℃の誤差を与えたと言うことです。
どうしたら、データ・クレンジングが合理的にできるかの思考実験です。
死なない程度に失敗したいデータ・サイエンティストは是非トライしてみてください。
2列目が目的変数で(恣意的誤差ありの)沸点のデータで、3列目以降がどんな原子団を幾つ持っているかの説明変数のデータになります。
まず、普通に行うことは、重回帰計算でしょう。
Excelにも搭載されているので簡単に試すことができます。
次のようなテーブルを瞬間で得ることができます。
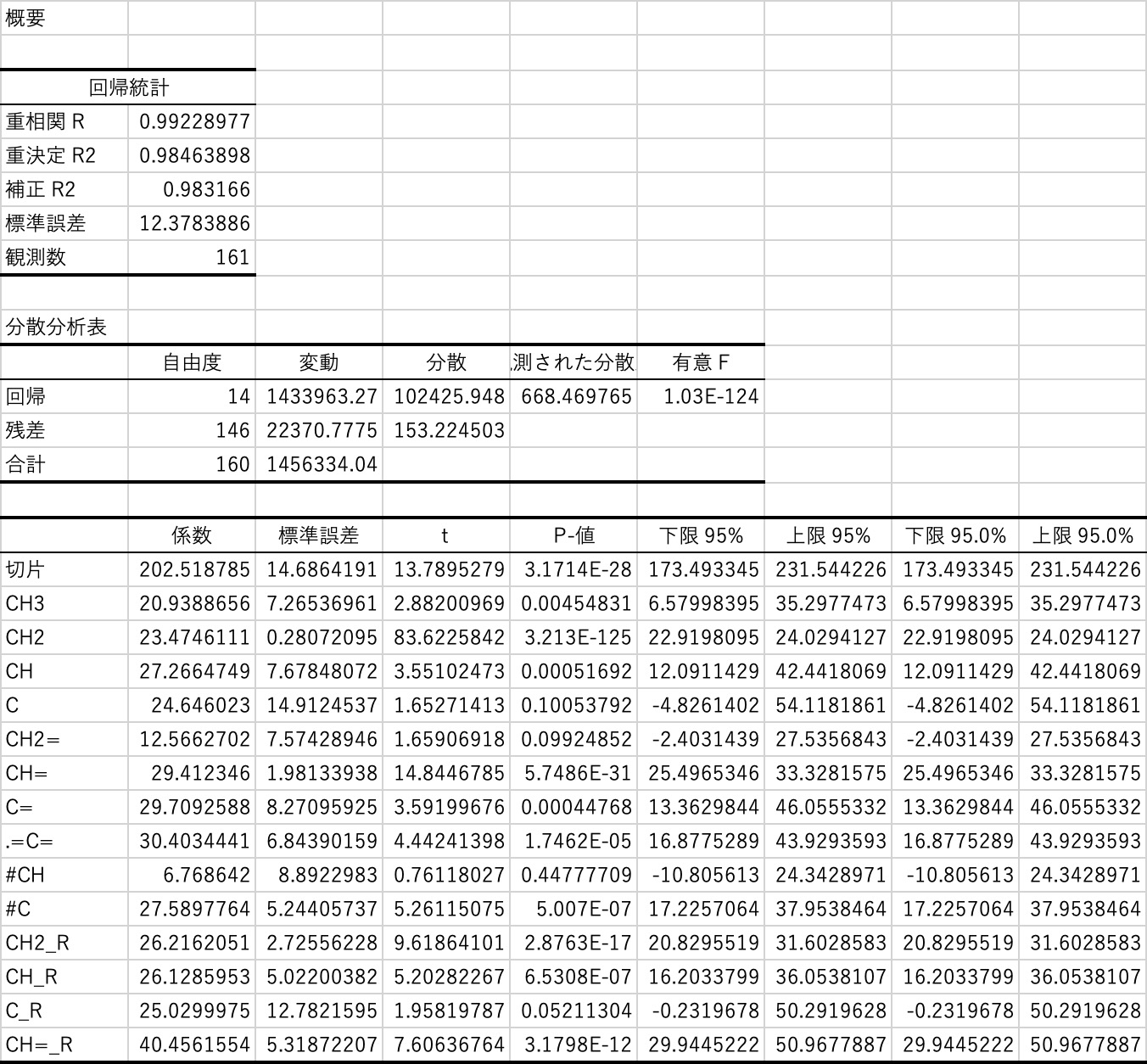
得られた統計諸量の意味を説明できるほど私は統計に詳しくないので、必要ならネットで調べてください。
大事なのは、このテーブルの中の係数です。
これが、先程のJOBACKの原子団寄与法の係数に相当します。
この係数が得られると次のように沸点の計算式を得ることができます。
BP=20.9388656019701*C2+23.4746111215847*D2+27.2664749306449*E2+24.6460229537968*F2+12.5662701961495*G2+29.4123460428614*H2+29.7092587901571*I2+30.4034441234816*J2+6.76864199961795*K2+27.5897763976479*L2+26.2162051043339*M2+26.128595302339*N2+25.0299974797523*O2+40.4561554413962*P2+202.518785333798イコール記号とその後ろをコピーしてエクセルの、どこか邪魔にならない2行目(参照する場所が、C2=C列2行目になっていることに注意してください)にペーストしてください。この式で計算された沸点が得られます。
全ての化合物を計算してグラフを書くと次のようになります。
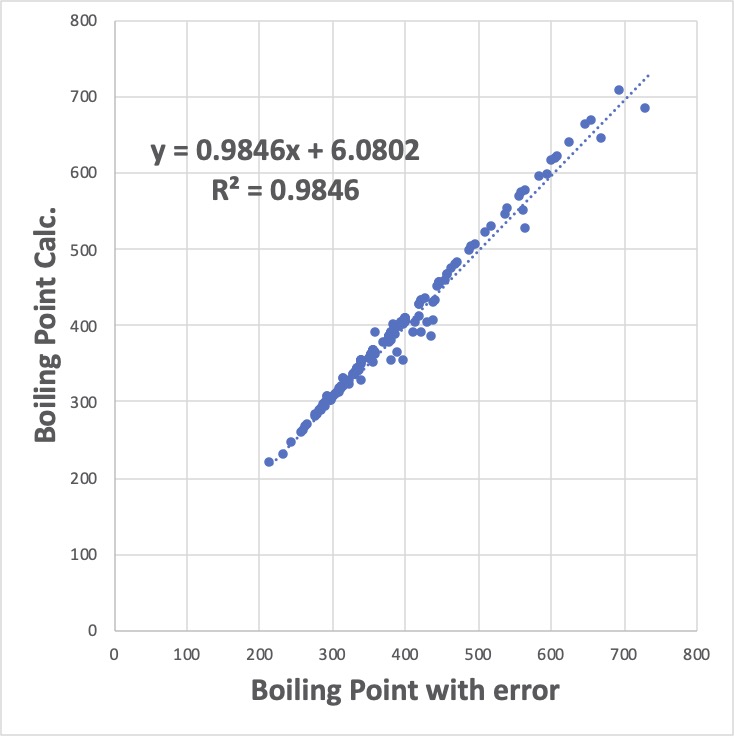
やりたいことは、このデータ値の中の恣意的にデータを改変した30分子を特定することです。ざっと見ると大きく外れる10分子ぐらいは見当がつくかもしれません。
注意していただきたいのが、データの改変の仕方です。元々あった真値に対して、乱数(0.0-1.0)に60℃掛けた値を足しているので、本来、近似曲線の右側に外れるはずです。
近似曲線は、ほぼ、Y = 1.0*X+0 の直線で、相関係数の二乗(決定係数)も0.9846とそれなりに精度は高くなります。
問題は、特に値が大きい所で顕著ですが、多くのデータ・ポイントが直線の上方へずれています。
これがある意味、重回帰法の最大の欠点です。
重回帰法は、Y = a*X+bの直線からのずれ(誤差)の二乗の総和を一番小さくするように動作します。(そこで、最小二乗法とも呼ばれます。)
本来は誤差は直線の右側だけに最大60℃あるのですが、60^2 は3600と非常に大きいので、重回帰係数を調整して、その誤差を小さくするように動作します。具体的には、沸点の大きな化合物30個に、(直線の左側に)10の誤差を与えても、30*10^2 で3000なので、3600より小さくなります。
なんとなく、見栄えが良い、全体的に誤差の小さなモデルを与えるのが重回帰法になります。
この性質は、データ群の中に信頼できないデータが混入していて、それを取り除きたい時には非常に困った性質と言えます。
最近、頂いたメールの肩書を見ると、MI推進室、データ・サイエンス部、AI推進チームなどが増えてきました。化学系の会社でそうした仕事に携わっているのでしたら、当然、こうしたデータ・クレンジングはできて当たり前です。
やり方がわからなかったら、そうした部署の専門家に相談すれば良いでしょう。
人材やツールが無いので解析できないと言う方もおられるかもしれません。
チャンスです。
どういう考え方をしたら、この問題に解決を与えられるか?
自分にとっては、そうした「考えること」は非常に楽しいことで、ステイホームの最高の暇つぶしです。
考えても、プログラムに実装しようとすると、それなりのテクニックが必要になります。私が主催しているMAGICIAN養成講座では死なない程度に痛めつけられるので、お勧めはしませんし。
まー、もうしばらくすれば、「情報」が大学入試に入ってくるので、10年もすれば、こうしたことが普通にできる人材は溢れかえってくるでしょう。それまでの辛抱です。
GROVE解析ツール
さて、GROVE解析ツールです。
学生が、悔しがって、徹夜でプログラムをコーディングしたものが、やっと形になってきました。エクセルのマクロを書いたことがある程度で初めて、3ヶ月でここまでできるようになったのは立派です。
先程の恣意的誤差のある系を計算すると次のようになります。
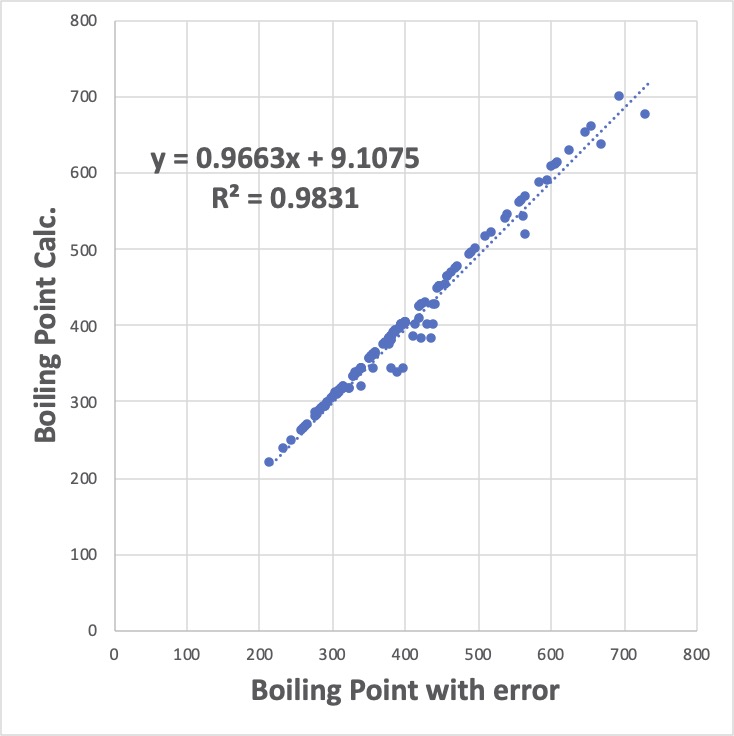
y = 0.9663x + 9.1075
R² = 0.9831
と傾きや切片の値は普通の重回帰(y = 0.9846x + 6.0802 R² = 0.9846)より悪くなっています。
決定係数も悪くなっています。しかし、GROVEで得た重回帰係数の方が圧倒的に優れているのです。
試しに、沸点300-500の間だけを拡大して見てみましょう。
左側が、普通の重回帰法の結果です。恣意的に与えた誤差の二乗の総和を小さくするために、誤差のないデータにも誤差を割り振っています。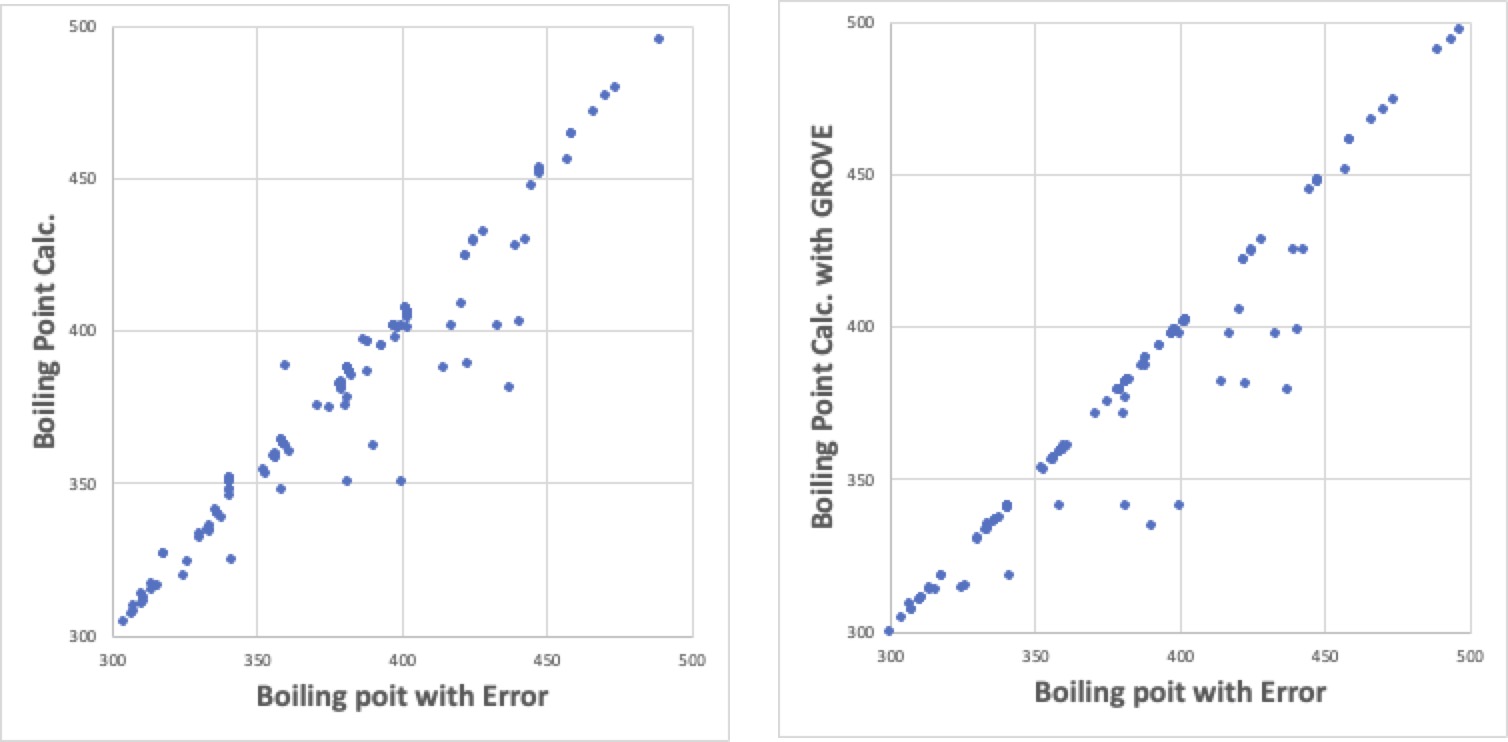
それに対して、右のGROVE解析結果では、Excelで近似曲線を取ると逆に悪くなりますが、誤差を与えなかったデータポイントは、ほぼ完全にY=1.0X+0の直線に載っています。そして、恣意的に誤差を与えたデータは、全て、1.0X+0の線の下に偏在します。
偏在の仕方が大きくなるので、統計的には決定係数や近似曲線が悪くなってしまうのです。
このツールを使えば、データ・クレンジングが容易になると言うのが実感して頂けるのではないでしょうか?
当然、得られた重回帰係数は、普通の重回帰法で得たものとは異なります。
例えば、工場で何かを生産しているとしましょう。品質保証課のCさんは、評価値をいつもちょっと大きめに出してしまします。
「運転条件と評価値のビッグデータが得られたので、AIに解析させて、評価値を最大にする運転条件を求めよう」
その時に、普通の重回帰法の係数を信じて運転最適化するのか、クレンジングすべきデータが入ったままでも、意図する係数が得られるGROVE法を用いるのか、結果は変わってしまうと言うことです。
GROVE法で線の上に乗らないデータを出しているのが、いつもCさんであることが特定できれば、Cさんの評価方法を他の人と擦り合わせる事も可能になります。
そうする事で、より豊かな生き方になるのがDXの本質ではないでしょうか。
例えば、GROVEを使ってオクタノール/水分配比率(logKow)を計算する重回帰式を作成してみます。

データソースはグリーンソルベントのカタログから持ってきたものです。
データは原子団寄与法のページにありますのでコピーしておいてください。
./GroupContribution.html
溶媒を構成している原子団のテーブルを作り、GROVE解析ツールで、まずは単純に重回帰計算を行います。
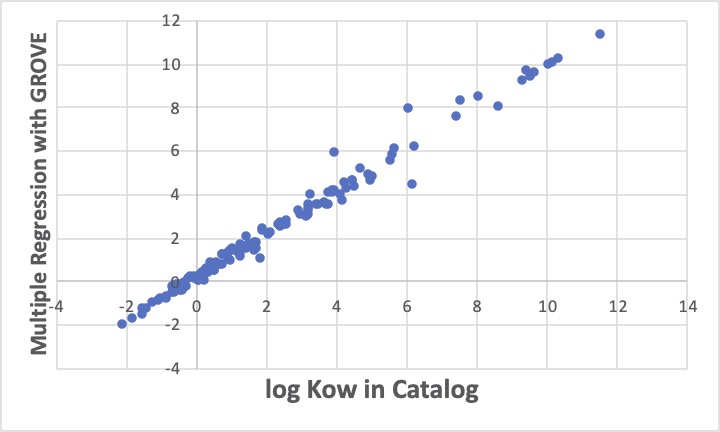
3つほど大きく外れる化合物が見つかります。これはこれで、他に正しい値が無いかを調べなくてはなりません。
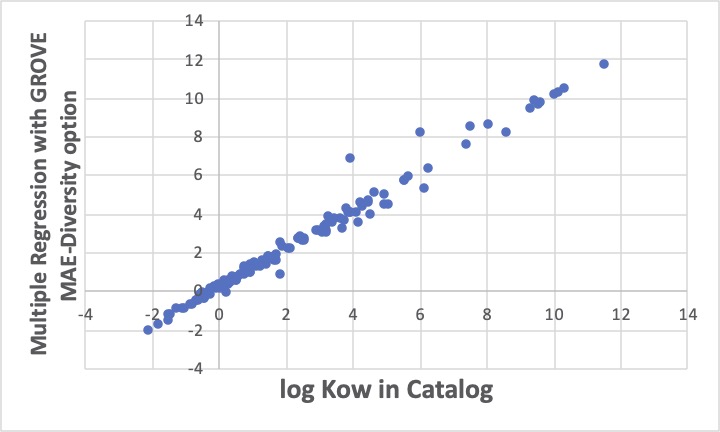
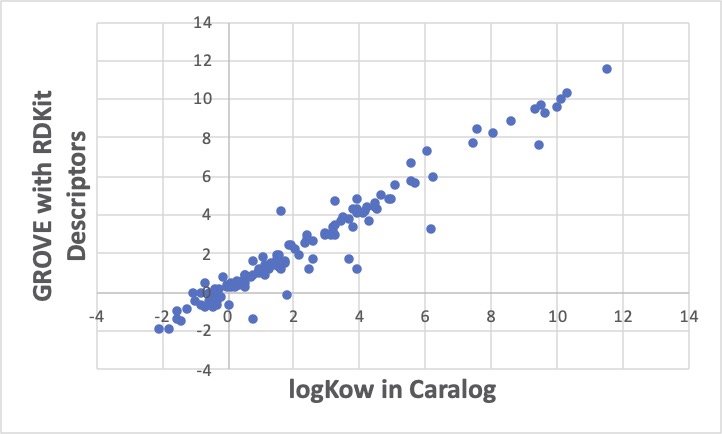
同じデータセットに対して、MAE-Diversity optionをつけて重回帰係数を探索すると上図のようになります。先程の恣意的な誤差の解析例と同じように、線に乗るものは、ますます線の上に乗り、外れるものは、ますます外れます。
統計諸量は悪くなります。
でも、外れるものが元の線に平行にずれているのを見ると、A社のグリーンソルベントカタログの中のlogKowの値は、C社とは測定法が違うのかな?とか色々考えることができます。(実際、logKowの測定法には、実際に抽出試験をする方法と、液クロを使った簡便法があります。)
GROVE法の1番の欠点は計算に時間がかかることです。 通常の重回帰法の何百倍も時間がかかります。
また、その解釈にもものすごく時間がかかります。
でも得られることも多いので、やる価値があるということです。
原子団寄与法のページでも、水への溶解度の推算式の構築を例に説明しましたが、データが無いので計算できない原子団、C_R(環状の4級炭素)のパラメータを決めておきましょう。
テーブルには、RDKitのトポロジカルな識別子も入れてあります。それを用いて予測式を作成して、仮決めしたC_R(環状の4級炭素)を持つ化合物のlogKowを用いて原子団の寄与率を計算するという方針です。
まず普通に重回帰計算をすると、なんとなく平均的に線の上に乗ったような結果が得られます。RDKitは普通の化合物であれば計算できるので、C_R(環状の4級炭素)を持つ化合物のlogKowを予測することができます。
Abietic acid, ethyl ester 631-71-0の予測値は、7.4になります。
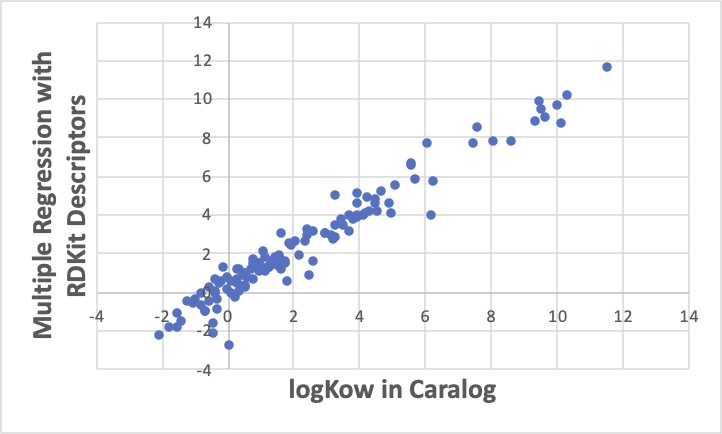
GROVE解析ツールが使える方はそちらで計算しましょう。線に乗るものは、さらによく乗り、外れるものは大きく外れて行くというGROVE法の特徴で、10個ぐらいは大きく外れます。原子団でみた時、RDKitでみた時、どちらでも大きく外れるものは、値を再チェックしましょう。
bietic acid, ethyl esterの予測値は7.7なので重回帰法と大きくは変わらないので、どちらを採用しても大きな差にはならないでしょう。
このGROVE法の開発をする際に、Clubhouseで学生とくっちゃべっていた時に、統計数理研究所の方が加わってくださいました。その時に頂いたアイデアを一つプログラムに実装しています。
前述のようにGROVE法は計算時間がかかるのですが、その時に重回帰係数がどのように変化して行くかを調べてみました。
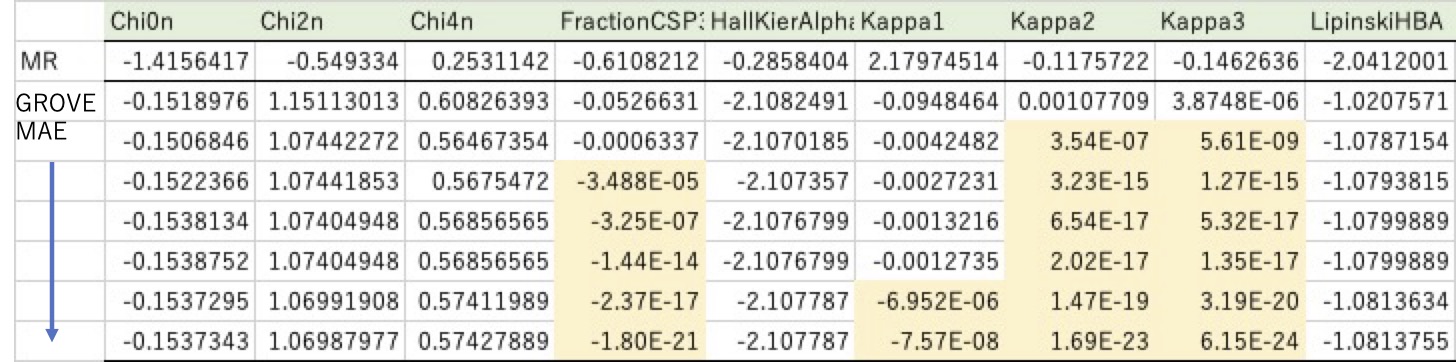
普通の重回帰法では計算は瞬間で、重回帰係数が求まります。その係数が大きいと言うことは、logKowの推算にその識別子は重要な役割を果たしていると考えることができます。(正確には係数と識別子の値を掛けたもので見ますが)
例えば、Kappa1の重回帰係数は2.18でKappa1の値も大きいので結果に大きな影響を与えると理解できます。
ところが、GROVE法で計算すると重回帰係数は全く異なるものになります。しかも計算が進むにつれその値が変わっていきます。
例えば、オレンジでマークした所見ると、どんどん0に近づいていきます。最終的には、Kappaは1-3まで全部0、FractionCSP3も0になってしまいます。このように13個あった識別子のうち4つは0、すなわちlogKowを推算するのに使わなくて良いとGROVEは言っていることになります。
通常、重回帰法は説明変数を増やすほど精度は高くなるので、増やしすぎないように注意しましょうと教科書は教えてくれます。
でも、どうやって精度を落とさずに識別子を刈り込むか?については何も教えてくれません。
普通のやり方では、重回帰係数と識別子の値から重要そうで無いものを取り除いて、計算して精度が落ちなければ次に移って識別子の必要性の判断をして行くのでしょうか。
でも、その方法では、Kappa1が取り除かれることは無いでしょう。
元々、普通の重回帰法で求めた係数では平均的には二乗誤差が一番小さい ですが、それを再現するには、Kappa1は重要なのですから。
GROVE法では10個ぐらい大きく外れる化合物があり、それ以外は良くY=Xの線上に乗っています。もしかしたら、その10個を線の上に近づけるのに大きなKappa1が必要なのかもしれません。しかし大きなKappa1を採用してしまうと他のものが皆、線上から押し出されてしまうのかもしれません。こうしたことを考える種を与えてくれるソフトはあまり存在しないと言うことです。
ニューラルネットワーク法を用いると、全部綺麗に線の上に乗ってしまうかもしれません。
それは、例えば、Kappa1の値をシグモイド変換するときに、小さな値はより小さい、大きな値はより大きい係数にすることによって実現されるのかもしれません。
しかし、中身は複雑なブラックボックスになってしまうので考える種は与えてくれないと言うことです。
まー、プログラムに実装するところまでは我々でもできたのですが、統計的な説明に関しては、統計数理研の方に頼らないと何とも我々には荷が重いのかもしれません。
現在のところ、MAGICIAN養成講座に参加している方限定でGROVE法を提供しています。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
