2019.1.22
情報化学+教育 > 情報化学 > PCA(主成分分析)
私は、数学が嫌いで化学の道に進みました。
そんな私がPLS法やPCA法を教えるのはもってのほかだと思います。
詳しい事は章末の書籍で自分で学んでください。
しかし、スマホの原理を知らなくてもスマホは使えます。
実際に使ってみてから、その解析手法がどんな特徴を持っているかを実感として身につけて行くのでも良いと思っています。
それに、実際に化学の領域の問題に適用した例題がとても少ないのが問題です。
せいぜい、スペクトルとオクタン価の問題を何十年も繰り返しています。
主成分分析に関するPirikaの記事
ブログ:
主成分分析@科捜研の女
「科捜研の女」榊まりこさんにAI機械学習を相談した。
配合処方解析用ツールMIRAIの成果
ドーピング規制薬物とカーネーション
動物を使った毒性評価は(意思を表示できる人間以外)禁止
3次元HSPから7次元HSP^2へ。DXを使ってHSP^2をAXしよう。
固定ページ:
化合物の皮膚浸透速度
主成分分析(PCA)を用いた次元縮退
PLS法の解析の章でも述べましたが、線形重回帰、主成分分析、PLS分析どれにも共通して言えることは、化合物の物性と分子構造との関係を解析したいということでしょう。
それを定量的に行うのが回帰分析だと自分は思っています。
要は求めたい目的変数(y)に対して、知りたいものの性質を表すものを説明変数(x)として、
y=function(X1・・Xn)
の関係を定量的に知りたいと言う事です。
主成分分析は逆行列を求めなくてはならない分、手間が大きくなります。
行列が大きくなってくるとPLSの方が有利になります。
逆にPLSには無く主成分分析にある特徴は何かあるのでしょうか?
それについてここで見ていきましょう。
ブラウザーバージョンのPCAプログラムを立ち上げてください。
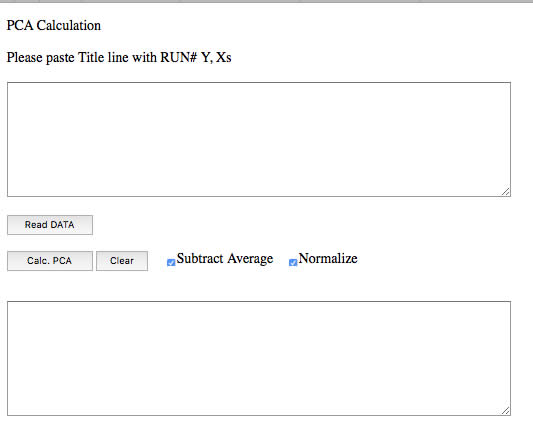
上のような画面が現れます。Subtrack AverageとNormaliseにチェックを入れます。
そして、まず最初はPLS法でもやった、スペクトルとオクタン価の関係をPCAで解析してみましょう。下記のテキストエリアのデータをコピーして表計算ソフトにペーストしておきます。
このデータは、1−36水準の近赤外のスペクトルデータと第2列目にはオクタン価が入ったテーブルになります。
つまり、目的変数はオクタン価、説明変数はスペクトル値となります。
これをPCAソフトの上部のテキストエリアにペーストします。(データはタブ区切りである必要があります。)
そしてRead Dataボタンを押して、Calc. PCAボタンをおします。このぐらいのサイズの計算であれば、結果はすぐに表示されるでしょう。
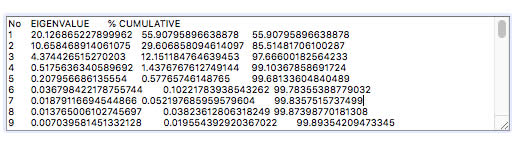
計算結果を全て選択して、テキストエディターにペーストしておきます。
結果のうちNo, Eigenvalue, %, Cumulative と書かれている部分を探してください。主成分をいくつ選択したらどのくらい現象を正しく記述できるかが示されています。
図で見てみましょう。
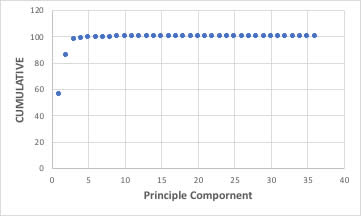
4つぐらいの主成分で99%以上記述できていることがわかります。
この意味を考えてみましょう。
もともとのデータは、36箇所のスペクトルデータから、1つのオクタン価に紐づけられているデータがありました。
つまり36次元ベクトルでした。
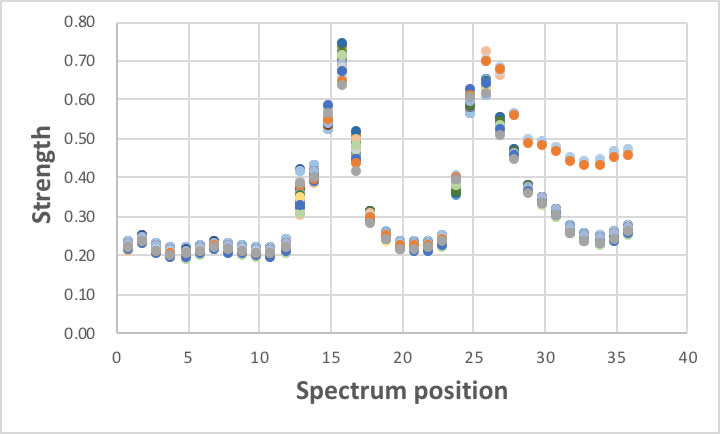
ところが、この36次元ベクトルはPLSの所でも示したように非常によく似たベクトルです。
人間は3次元ベクトル以上は頭の中に思い浮かべられないので、次元を下げることを考えます。
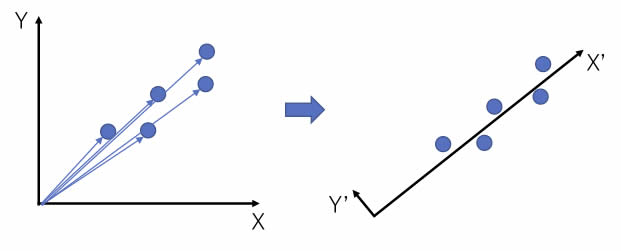
例えば、左の図では2次元のベクトルが5つあります。
ベクトルの大きさは異なるが、向きは非常に似ています。
そこで、X軸、Y軸を回転してあげると右のようになります。
X’軸はだいたい元のベクトルの大きさとなり、Y’軸は非常に小さな値になります。
Y’の値が十分小さければ、軸の回転によって2次元ベクトルを1次元ベクトルに下げたことになります。
元々36次元ベクトルあったものを、軸の回転によってどのくらい次元が下げられるか?
と言う質問に対して、PCA分析は、5つの大事な軸を使えば、99.68%元のベクトルを表現できると言う答えを返しています。
この大事な軸のことを5つの主成分と呼びます。
各軸は直交していることが必要になります。
直交と言うのはベクトルの内積がゼロであると言うことです。
元のX,Y軸も(1,0)*(0,1)で内積はゼロになります。
独立成分分析というのはこの内積がゼロという条件すら取り除いてしまった解析法です。
難しい話は、ソフトが皆やってくれる。大事な軸が幾つあるか?だけに集中しましょう。
ここまでの話は、オクタン価(yの値)は全く使っていません。
そこがPLSと大きく違う所です。
説明変数がたくさんあるときに、説明変数を減らす事ができるというだけのことです。
y=function(X1・・X36)
y=functionB(X’1・・X’5)
最初に述べましたが、やりたい事は定量的にオクタン価を予測する回帰式を得ることです。そこで、大事な軸5だけを使ってfunctionBを求めてあげる事を考えなくてはなりません。
そこで、X1-X36からX’1-X’5へ変換したテーブルを作る必要があります。
元のテーブルは、Subtrack AverageとNormaliseで規格化されています。
PCA計算結果のConverted inputを抜き出してExcelにペーストしておきます。

先ほどのPCA計算結果の中のCalculate Schemeを抜き出してきます。
第1主成分は、0.2100103141999724*C2+0.21570854997480743*D2+.... -0.09923093239537442*AL2
で表されます。これは表計算ソフトの計算式そのものなので、Converted inputテーブルの後ろの方の2行目にペーストします。
そして、C列からAL列の値をPC1-PC5に変換したテーブルを作成します。
PLS法と違って有利な点は、このテーブルの変換はy(オクタン価:B列)を使っていないので、予測したいスペクトルも変換できる点です。
(PLSではそれ用のプログラムを書かなければなりませんでした)
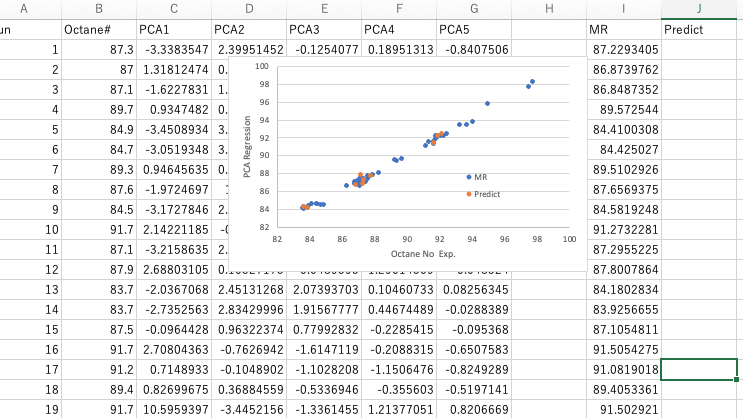
主成分5つのとオクタン価のテーブルを作り、重回帰解析を行えば上図のように簡単に主成分回帰の結果が得られます。
PLSの結果(下図)と比べてもほとんど変わらない結果となります。
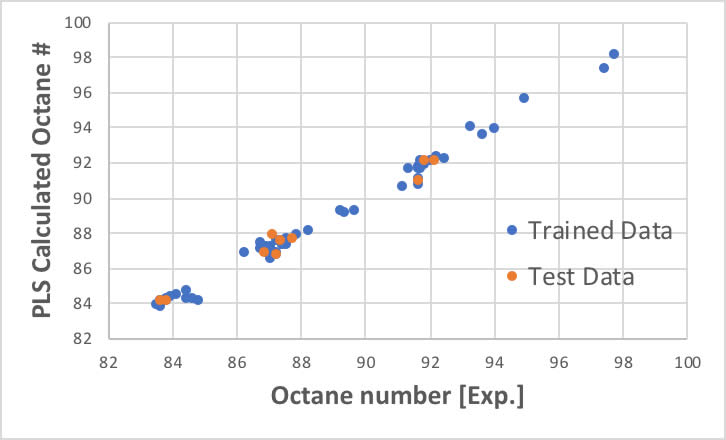
定量的解析では、PLSでは予測値を得るのに、プログラミングの知識が少し必要になります。
どちらを使うかは好みとも言えるでしょう。
定性的解析では、重要な軸を使って、化合物を分離(毒がある、ない、燃える、燃えない)するには主成分分析の方が多く使われているような気がします。
まーどちらも使えるに越した事はないのでしょう。
次にPLSと同様に有機化合物の水への溶解度を検討してみましょう。
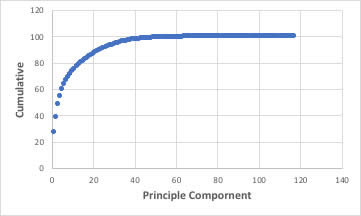
RDKitの出力、117識別子を使った場合には、次元数40まで減らせる事がわかります。
(40の時に97%を超えるからといって、水への溶解度の推算精度が高いわけではありません。この段階では、水への溶解度のデータは使っていません。)
40主成分を使って重回帰計算を行うと以下のようになります。式を作るのに使わなかった化合物を予測してみるとそれなりに推算できています。
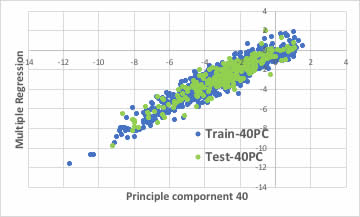
PLS法ではNP15で評価しました。
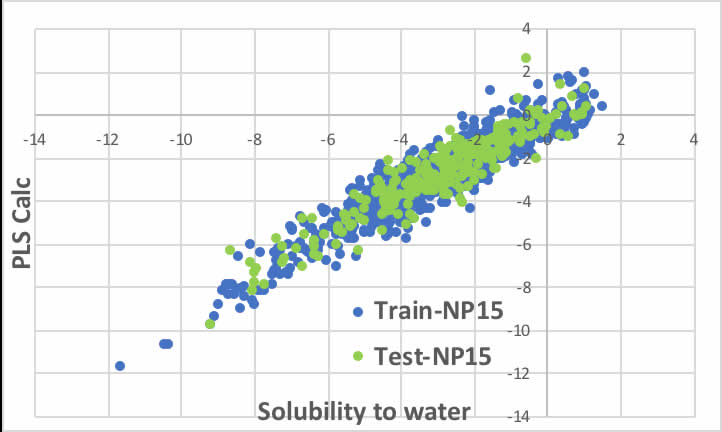
そこでPCAでもPC15で重回帰式を作成してみます。
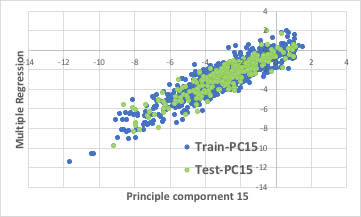
少しPLS法の方が良いような気がします。
このようにPCA法とPLS法は親戚関係のような解析法なので、目的に合わせて使いこなして行けば良いと思います。
大事なのは、RDKitの識別子だけでは精度はいまいちで、さらに良い識別子を探せるか?でしょう。
ニューラルネットワーク法などの機械学習をすればもう少し見かけはよくなると思います。
しかしその方法では、データが増えてくれば予測性能が必ず低下します。
本質的な水への溶解度を上げ下げする識別子を探す方が結局は早道です。
プログラムのタネ本は、「Excel VBAによる化学プログラミング、佐藤寿邦・佐藤洋子共著 培風館 2002年」です。
ここに記載のVBのプログラムをJavaScriptに変換しました。
主成分分析に関する書籍はPLSのものとかぶります。
- ケモメトリックス 化学パターン認識と多蛮量解析 宮下芳勝・佐々木慎一著 共立出版 平成6年
- 化学者のための多変量解析 ケモメトリクス入門 尾崎幸洋・字国明史・赤井俊雄/著 講談社サイエンティフィク 2002年
- ケモインフォマティックス 予測と設計のための化学情報学 J.Gasteiger・T.Engel 編 船津公人 監訳
船津 公人 ・佐藤 寛子 ・増井 秀行 訳 平成17年 - これならわかる化学のための統計手法 丹羽誠 化学同人
- 多変量解析の考え方 井上勝雄 筑波出版会
- 多変量解析の展開 甘利俊一ら 岩波書店
- 多変量解析ハンドブック 柳井晴夫ら 現代数学社
- 多変量統計解析 田中豊ら 現代数学社
色々な本で勉強したが、本質的に数学は嫌いなのでモノにはならなかった。。。
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
