2018.9.25
情報化学+教育 > MAGICIAN 養成講座 > 講義資料 > 第6a回 ニューラルネットワーク法の基礎
MAGICIAN(MAterials Genome/Informatics and Chemo-Informatics Associate Networks)
MAGICIANとは、材料ゲノム(Materials Genome)、材料情報学(Materials Informatics)、情報化学(Chemo-Informatics)を結びつけて(Associate)ネットワーク(Networks)を構築していかれる人財です。
Materials Genomeを使って何か素材を設計したいとしましょう。
Genomeというのは遺伝子のことで、素材を遺伝子解析してより優れた素材を探索するのがMaterials Genomeの語源です。
それでは、素材のある部分の遺伝子をいじった時に、結果がどうなるか? は、どうしたら解るでしょう?
実際にハイスループットで実験を行うとか、Net, 論文, 特許を検索してデータを集めるのでしょう。
そうして集まったデータを統計解析して、予測式を立てて、より良い素材になるように改良していきます。
???
昔から行われているこうした統計解析の方法と、Materials Genomeの方法はどこが違うのでしょうか?
実は全く変わらないのです。
筆者は20年前から、「物性推算(Properties Estimation)と逆設計(Reverse Design)」と呼んでいました。
筆者が多用している物性推算法はニューラルネットワーク法であり、多用している逆設計法は遺伝的アルゴリズム法です。
ニューラル(神経細胞)、遺伝などの言葉が入っているので、まるで生物の進化に関係があるように聞こえますが、単なる統計解析法の1種とも言えます。
画像解析や自然言語解釈などは、ネットの発達によって非常に容易にビッグデータが入手できるようになりました。
「猫のヒゲとはなんぞや?」という問いに膨大なデータが集まります。
しかし、素材のある部分をいじったときの結果はどこを探しても見つかりません。
そこで、なるべくデータは集めるにしても、足りない部分は合理的な方法で補完することが必要になります。
一つの方法は、分子軌道計算や分子動力学計算によってデータ数を増やすことです。
しかしこれらの方法は、第3回で紹介したような、市販されているカーボンブラックの品番によってゴムの性能が変わるなどには適用できません。
残念ながら、現時点では王道はないのだと思います。
開発したい素材に合わせて、化学の知識を総動員してMaterials Genomeを行っていれば、AIに仕事を奪われるようなことはないでしょう。
そう言い切れるためには、まず、ニューラルネットワーク法による物性推算の基礎を学びましょう。
第7回で、遺伝的アルゴリズムについて解説します。
ニューラルネットワーク法の基礎
ニューラルネットワーク法の基礎については、筆者のHP、
https://www.pirika.com/
に多分2005年ぐらいに記載しています。
コンピュータによる知識の獲得
ニューラルネットワークの基本
ニューラルネットワークはどう学習するか
ニューラルネットワークの問題点
これらのページを既に読んでいる学生は、前半は読み飛ばしても良いです。
ただし、HPは15年近く前の記載なので、細かいところは変更になっています。
(ちなみに、pirika.comのHPは来年で2019年で20周年になります。物好きの趣味のページがこれだけ長続きしているのも、付き合ってくれる読者があってのことです。だいたい1日あたり10,000ページ、世界中から訪ねてくれます。誰かお祝いでもしてくれないものでしょうか? 閑話休題)
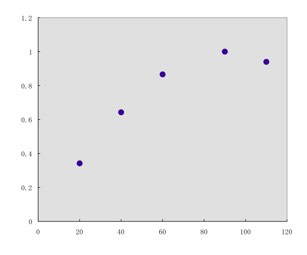
下の図のようなX−Y関係のデータポイントがあったとします。
化学系の研究者が最も一般的に用いる解析方法は、(重)回帰計算でしょう。
これは最小二乗法とも呼ばれる技術です。
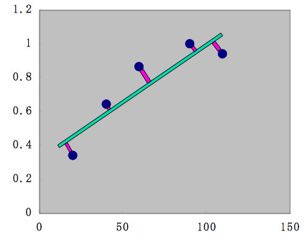
重回帰計算を簡単に説明すれば、下の図に示すように、緑色の直線、Y=aX+bを仮定して、この直線からの誤差の2乗が最低になるaとbの組を見つける計算です。
(出典を見ると直線Y=aX+bに対してXは一定で線を下ろしたときの2乗だとか色々な定義があるようです。まー、数学者でない者のたわ事と読み飛ばしてください。)
計算自体は非常に簡単で、Excelなどの表計算ソフトにもその機能が搭載されています。
多くの場合、化学の現象を扱うのはこの重回帰計算で十分です。
しかし、計算によっては非線形性を導入しなくてはならない場合があります。
実は、上の図の青い点は下に示すようにSinカーブの一部でした。
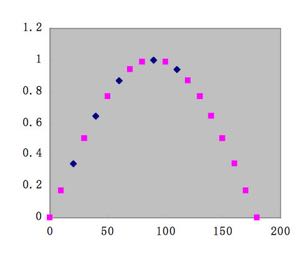
これを正しく扱いたい場合には、非線形回帰計算を行う必要があります。
そこで、先ほどの重回帰計算と同様に、
f(y)=A1* / [1+exp(-(B1*X1+B2*1))+
A2* / [1+exp(-(B3*X1+B4*1))+
A3* / [1+exp(-(B5*X1+B6*1))
という曲線を仮定して、誤差が最小になるA1-A3, B1-B6の組を見つければ良いことになります。
曲線としてどんな曲線を仮定するは各人の自由です。
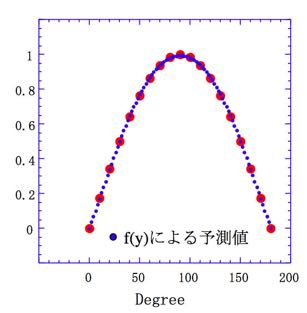
例えば、
A1= -2.14 B1= -1.84 B2= 0.30
A2= -1.01 B3= 0.04 B4= 0.31
A3= 2.11 B5= -1.87 B6= 1.57
だとすると、下図に示すように良好にSinカーブを再現します。
このf(y)をを模式的に書くと、生体の神経細胞(ニューロン)がつながったような図になります。左の2つを入力層ニューロン、真ん中の3つを中間層(隠れ層)ニューロン、右の1つを出力層ニューロンと呼びます。
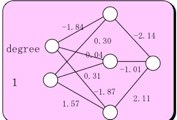
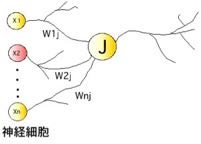
式中の変数、A1-A3, B1-B6は模式図中でニューロンを同士の結合の強さ(結合荷重行列と呼びます)として表わされています。
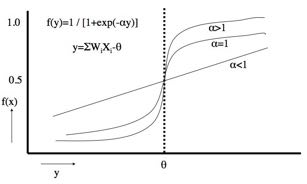
また、f(y)=A1* / [1+exp(-(B1*X1+B2*1))という関数は、シグモイド関数と呼ばれ、αの値によって、ある閾値θで急に値が変わる関数になります。
これは、生物の刺激ー応答曲線に似ているため、ニューラルネットワーク法と呼ばれています。
このシグモイド関数をいくつ(Sinの場合は3つ)足し合わせるかで、複雑な現象に対しても良好にフィティングを行うことができるようになります。
ただし、シグモイド関数をむやみに増やすと、後述するように、様ざまな弊害ももたらされます。
それでは、この、A1-A3, B1-B6の組はどうしたら求まるでしょうか?
重回帰法の場合は、連立方程式の解法なので、方程式を行列表現にして、逆行列を求めれば係数はすぐに求まります。
非線形回帰式は、数学的な解の式が求まらないので、収束計算を行います。
最初の重回帰の式、緑色の直線、Y=aX+bのa,bを収束計算で求める事を考えてみましょう。
データ点は5点あります。
それから2点選ぶには、5C2の組み合わせがあるので10種類のa,bの組みが求まります。
その10種類の直線のうち、一番トータル誤差の小さな直線がどれかは、簡単に解ります。
5点全部の誤差の2乗を足し合わせ、最小のものが初期値になります。
次に初期値の直線で一番誤差の大きい点を特定して、誤差が少し小さくなる方向に、Δa, Δb動かします。
そしてトータル誤差を計算します。
これを繰り返していくと、(途中で最大誤差を与えるポイントは入れ替わるかもしれないですが)一つのa, bに収束していきます。
ニューラルネットワーク法の収束計算も、これと同じ方法をとります。
単なる収束計算ですが、誤差逆伝播学習法(Error Back Propagation)というもったいぶった名前がつけられています。
20年前にニューラルネットワーク法がブームを迎えたのは、このEBP学習法の性能がよかったからと言われています。しかし、その後廃れてしまったのは、EBP学習法の問題点を解決できなかったからだと思います。
20年の時を経て、ビッグデータがあればという条件付きでディープラーニングというニューラルネットワーク法が復権したのは感慨深いです。
コンピュータは人間と違い、飽きることを知らないので、命令すれば一晩中でも、1年でも学習を続けます。
すると、本来欲しい点はピンクの点であるのに、最終的には学習した点をなめらかにつなぐ緑の線を答えとして提案します。
学習に使ったデータでは相関係数R=1.000、”おおー、ものすごく良くモデルを再現できる式が構築できた”と喜んで論文に投稿したりします。
でも、下のグラフを見れば明らかなように、学習した近傍以外は非常に悪い答えを返すモデルです。これなら、重回帰のほうがまだまし、っていうレベルです。
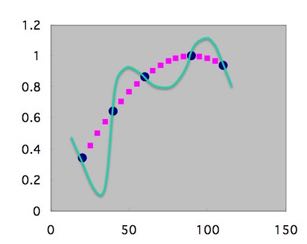
このような、学習状態を過学習といいます。
過学習は学習のデータポイントが少ない、NNの中間ニューロン数が多すぎるときに起こりやすいです。
そこで、ピンクの点も含めて学習させてしまうことを考えます。
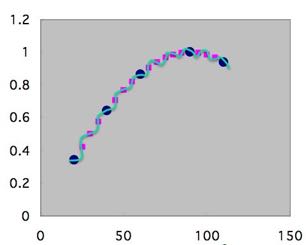
このようにデータ数が増えてくれば大きくハズレる曲線は取りようがなくなります。
つまり、ビッグデータがあればニューラルネットワーク法の過学習は抑えられるのは、昔から分かっていました。
問題は、新素材を考えなくてはならない化学の領域では、なかなかビッグデータが集まらないことです。
それは今も昔も状況は変わっていません。
中間層のニューロン数は、何個シグモイド関数を足し算して、この現象を表現しようとしているかを表しています。
当然ニューロン数を増やせば複雑な現象にも追随できますが、その分、過学習という、やっかいも背負いこむことになります。
こうした、中間層のニューロン数の最適化とデータポイントの数、これが考慮されずにニューラルネットワークを組んでも、無駄です。
それを評価するのに赤池情報量基準(AIC)というものも知られていますが、難しすぎて自分には理解出来できていません。
それに、化学の現象はそれ以前に多くの、誤差、あやふやさを含んでいます。
極端なことをいえば、熟練工のAさんと新人のBさんが同じ手順書にしたがって実験を行っても結果が異なります。
AICを考えるよりも、実験者A,Bをニューラルネットワークに入れる方が結果はよくなります。
もう一つ、ニューラルネットワーク法が廃れた理由は、予測性の欠如です。
先程のSinカーブの学習で、Sinの頂点までしか学習しなかったとします。
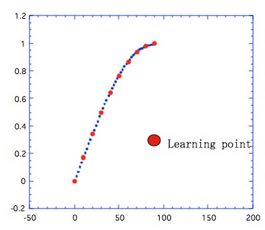
そうした場合は、学習した内側については、中間ニューロンの数が適当であれば、青い点が示すように良好に予測することができます。
これは、”内挿問題に対する予測性”は高いという言い方をします。
しかし、θが90を超えた先がどこに行くのかは、NNには判りません。
したがって1点でもよいから90度以上のデータを入れる必要があります。
これは実は先程の過学習よりも、よっぽどたちが悪い現象です。
例えば、化合物の官能基を定義して沸点を推算するNNを構築しようとします。
ある官能基、例えば水酸基を持つ化合物の沸点のデータが、水酸基が1,2,3個もつ化合物の沸点データがあり、NNに取り込んだとします、その場合は分子中に水酸基を4つもつものは、”外挿” 問題になり、予測性は高くないだろうと見当がつきます。
ところが、カルボン酸を1-2個もつ化合物、アミノ基を1-2個持つ化合物をNNに組み込んでも、分子中に、カルボン酸とアミノ基を両方もつアミノ酸をNNに組み込んでいなければ、これはやはり外挿になってしまいます。
こうした”組み合わせ”外挿はどれだけあるのかは、一般的に言えないし、非常にむずかしい問題です。
また、アミノ酸のように、ひとつの炭素にカルボキシル基とアミノ基が付いている場合、遠く離れて付いている場合でも物性値は大きく異なります。
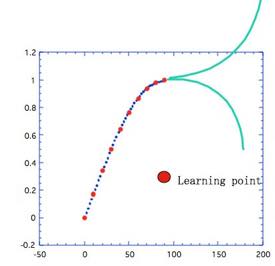
従って、NNで物性推算式を構築した場合には、どのような母集団からNNを構築したのかが非常に重要な問題になります。
この場合でも、ビッグデータが存在すれば問題は解決します。
しかし、”組み合わせ”外挿を全て網羅するようなデータベースは残念ながら存在しません。
画像解析や自然言語解釈では上手くいったディープ・ラーニングですが、マテリアルに適用するのであれば、アプローチを変えなくてはなりません。
実際の適用例
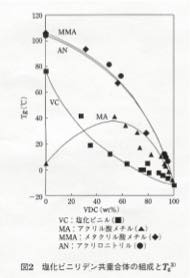
第4b回でバリアー性素材のガラス転移温度(Tg)の予測を取り上げました。
ビニリデンクロライド と他のモノマーの共重合を考えた場合、アクリル酸メチルとの共重合体の場合だけ、Tgが上に凸になる現象がありました。
この曲線は見ようによるとSinカーブの一部のように見えなくもありません。そして、先ほど述べたSin曲線の頂点の先の1点が与えられています。
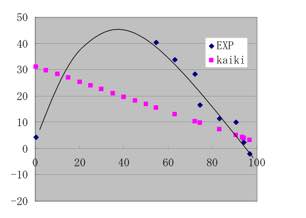
当然のことながら、重回帰法では直線しか表現できないのでフィティングすることはできません。そこで2003年当時用いていたニューラルネットワーク法のプログラムを使って解析したところ、中間層数が2では収束せず、3とか4では過学習を起こしてしまうことが判明していました。
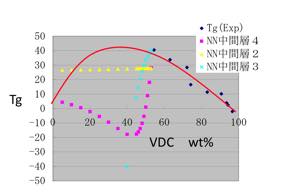
当時のニューラルネットワークの実力など、この程度でした。
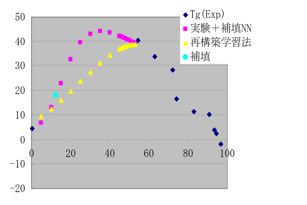
そこで、こうしたデータ数が少なく、過学習になりやすい系を扱うときは、様ざまな工夫を駆使したものでした。例えば、VDC10%の値をデータに補填してあげると、過学習が抑えられるであるとか、再構築学習法をとれば、データ補填をしなくても上に凸を表現できるであるとかです。
「中間層が多い場合、過学習を起こし、データを滑らかにつないでしまう」これを確認するために、自作のNNシミュレータで再計算してみました。
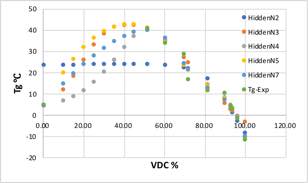
中間層が2の時には全く収束しません。
しかし3以上の時に過学習を起こす事もありませんでした。
何故だかは不明ですが、中間層が4の時だけ挙動が異なります。
15年かけて、シミュレータを改良してきたので、データ数が少なくても過学習は起こしにくいシミュレータに進化したようです。
シミュレータを進化させるには、自分でプログラムが書ける必要があります。
しかし、化学系の学生にはそれはきついかもしれません。
でも、プログラムを書くなどというのは、そのうち、AIが幾らでもやってくれるので心配することはありません。
問題は、「そのうち」というのが何時かということです。(2024年:ChatGPTのプログラム作成能力は私を追い抜いています。そのうちが来ました。)
それまでは、今できることをやっておきましょう。
シミュレータをいじらなくても今できることは、入力データを工夫することです。Sinカーブを予測する例で入力データの工夫のしかたを示しましょう。
Sinカーブは、シグモイド関数を用いれば、
f(y)=A1* / [1+exp(-(B1*X1+B2*1))+
A2* / [1+exp(-(B3*X1+B4*1))+
A3* / [1+exp(-(B5*X1+B6*1))
A1= -2.14 B1= -1.84 B2= 0.30
A2= -1.01 B3= 0.04 B4= 0.31
A3= 2.11 B5= -1.87 B6= 1.57
とすれば、精度高く予測可能でした。
その時の説明では、シグモイド関数を選択するか、他の関数を選択するかは自由だと述べました。
それでは、
f(y)=A1*(1/X1)
+A2*log(X1)
+A3*(X^2 )
+A4*(sqrt(X1))
とした時の、A1-A4を求めてみましょう。
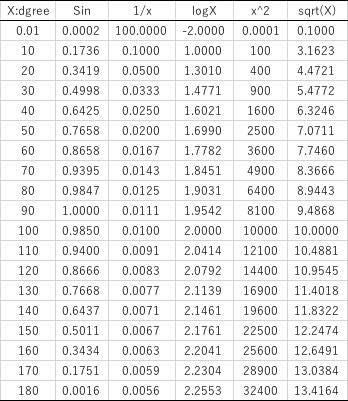
この係数を求めるのは非常に簡単で、普通の重回帰計算を使えば良いです。
上記データから、重回帰計算を行えば、重回帰係数が求まります。
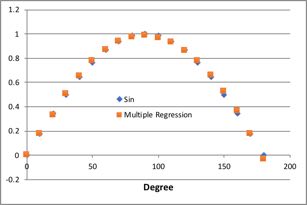
厳密なSin計算値に対して、重回帰計算結果はほぼ完全に重なります。つまり、入力値を工夫すれば、非線形の曲線であっても重回帰の形で表すことができます。
A1-A4、定数が幾つになったか控えておきましょう。
(ただし、X1=0.0の時には、1/X1がエラーとなるのでX1=0.0は計算できません。)
このように、過学習や予測性の欠如の問題を抱えながら、無理やりニューラルネットワーク法を使う必要はありません。
かといって、無理やり1/Xだのlog(X)などの非線形関数を使う必要もありません。
例えば、ある温度での蒸気圧をフィティングする式として、Antoine式というものがあります。
log P(mmHg) = A – B/(T℃ +C)
A, B, Cは化合物特有の定数としてフィティングされます。
この、Antoine定数には物理化学的な意味があります。
例えば Antoine Bは化合物の蒸発潜熱と相関があります。
Antoine Cは沸点と相関があります。
ところが、最近開発されている蒸気圧式は、
log P = A + B/T +C|log10T + D|T + E|*T^2
などとなっています。
この場合のA-Eは単なるフィティング・パラメータであって物理化学的意味はありません。
しかし、Antoine A, B, Cパラメータは素材を設計する際に非常に有用なパラメータとして重用されます。
また、何故、ある化合物ではAntoine式では不十分なのか? を考えることによって、その化合物特有の分子間力を定量的に見積もることができるようになります。
課題
超臨界炭酸ガスの密度は、温度圧力によって急激に変化します。
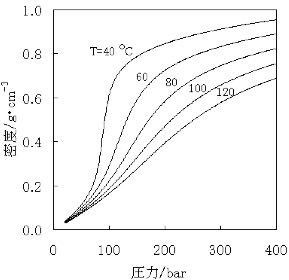
例えば、密度が0.18から0.5の間にはいる領域は、Miracle Densityと呼ばれ、化学反応が特異的に促進される密度として知られています。
温度と圧力は計器の測定値としてわかるとして、ある温度、圧力の時の密度の予測値を求める式を作ってみましょう。データー点をデジタイザーで取り、ニューラルネットワーク法で計算すれば、すぐに収束するでしょう。
次に、Sinカーブの時と同じように、入力値を工夫することによって、重回帰法で予測する式を作成し提出してください。
雑感
シミュレーションは、よく合うものについては、全く面白くありません。
あとはAiにでも任せれば良いと思ってしまいます。
ある理論でシミュレーションしたのに合わないものにこそ、研究する価値のある未知の何かが隠されていると信じています。
先日新聞を読んでいたら似たようなことが書いてありました。
「論理的に考えるように」という言葉はよく聞く。それは間違いで、論理では解き明かせないから考えるのだと。
考えることによって「今の論理」では説明できない現象に対して「新たな論理」を組み上げるのが知的生産なのだと。
ニューラルネットワークは、中がブラックボックスで、何故だかわからないが合ってしまうので、気付きがなくなりがちになります。
気をつけないと、中身のない薄っぺらな研究者になってしまいます。
シミュレータを工夫するか、入力を工夫するかして、化学の知識を総動員して、かつ、AIにアシストしてもらい、何故、VDC-MAのTgが上に凸になるかを理解しなければ、次にどんなモノマーを使ったら良いかはわかりません。
かといって、無視できる技術かといえば、そんな甘いものでもありません。
化学の地力も持っている者がAIアシストを受けて、気づきを得られるなら鬼に金棒なのだと思います。それまでは,実験科学者とよく相談しながら協業するのでしょうか。
情報化学+教育 > MAGICIAN 養成講座 > 講義資料 > 第6a回 ニューラルネットワーク法の基礎
Copyright pirika.com since 1999-
Mail: yamahiroXpirika.com (Xを@に置き換えてください) メールの件名は[pirika]で始めてください。
